В продолжение темы о рассчетах взлета с трамплина
785
Дискуссия
новая
|
|
mirok ( Слушатель ) |
| 19 окт 2016 в 00:44 |
Начало тут
Я проглядел эту ветку, поэтому начал не там малость... Если модераторы смогут перенести тамошние посты по этой теме сюда - был-бы благодарен...
Вобщем по моим понятиям получается что для точного рассчета надо знать:
1. зависимость тяги двигателя от скорости
2. зависимость подъемной силы от скорости, высоты и угла атаки.
3. Зависимость силы сопротивления набегающего потока воздуха от скорости и угла атаки.
Зная эти зависимости можно численно смоделировать взлет и высчитать траекторию полёта.
В принципе можно попытаться даже просчитать оптимальные параметры - угол наклона трамплина, угол атаки, может даже было-бы оптимально не держать тангаж постоянным, а менять его со временем... Всё сугубо ИМХО, я аэродинамику не изучал, но более-мение понимаю обычную динамику и имею опыт численного моделирования.
Я проглядел эту ветку, поэтому начал не там малость... Если модераторы смогут перенести тамошние посты по этой теме сюда - был-бы благодарен...
Вобщем по моим понятиям получается что для точного рассчета надо знать:
1. зависимость тяги двигателя от скорости
2. зависимость подъемной силы от скорости, высоты и угла атаки.
3. Зависимость силы сопротивления набегающего потока воздуха от скорости и угла атаки.
Зная эти зависимости можно численно смоделировать взлет и высчитать траекторию полёта.
В принципе можно попытаться даже просчитать оптимальные параметры - угол наклона трамплина, угол атаки, может даже было-бы оптимально не держать тангаж постоянным, а менять его со временем... Всё сугубо ИМХО, я аэродинамику не изучал, но более-мение понимаю обычную динамику и имею опыт численного моделирования.
Отредактировано: mirok - 19 окт 2016 в 00:56
- +0.03 / 1
-
ОТВЕТЫ (25)
|
|
Artkonstruktor ( Слушатель ) |
| 19 окт 2016 в 18:51 |
Цитата: mirok от 18.10.2016 22:44:46
Помница года так три назад, мы с комрадами уже пытались решить подобную задачу.
С тех пор много воды утекло...
Присутствие на различных ветках значительно обогатили наш опыт.
Поэтому можно приступить к более осмысленным расчетам.
Для взлета самолету необходимо набрать необходимую скорость.
Vотр = sqrt(2*G*g/p*Cy.взл.*S)
Для ее определения необходимо задать исходные данные.
G - взлетная масса.
У Су-33 масса пустого 16000 кг.
Масса топлива 9400 кг.
Боевую нагрузку давайте примем 4 ФАБ-250 + 2 Р-73 + 2 Р-27
4*260+2*105+2*253=1136 кг
ИТОГО взлетная масса 26536 кг.
q - ускорение свободного падения 9,8 м/с2
Суотр - коэффициент подъемной силы.

Тут все туго.
Он зависит от угла атаки.
Надо напомнить, что при движении по палубе, при сходе трамплина и до верхней мертвой точки аэробаллистической траектории, он равен установочному.
И только при просадке достигает максимального значения.
При взлете Су-27 с с бомбардировочными средствами поражения и НРС, накладывается эксплуатационные ограничения по углу атаки в 20*
Поэтому значение коэффициента будем считать для данного параметра.
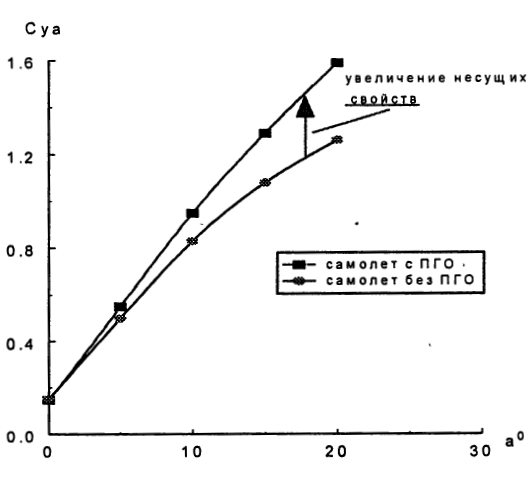
Если верить этой поляре, то Су Су-27 при угле атаки составляет 1,2
В книге Основы методологии аэродинамического проектирования маневренного многорежимного самолёта-истребителя про Су-33 сказано, что благодаря установке ПГО и изменении механизации крыла удалось повысить коэффициент подьемной силы в 1,5 раза.
Соответственно оно должно было достигнуть 1,8 при 20*
Точных данных нет, но с учетом запаса предлагаю принять следующие значения:
На разбеге Суотр = 0,15
При просадке Суотр = 1,6
Плотность воздуха p =1.225 кг/м3
Площадь крыла S =62 м2
Подставляем значения и получаем необходимую скорость 65,42 м/с или 235,5 км/час
Т.е. наша задача, на верхней точке аэробаллистической траектории, обеспечить данную скорость.

- +0.31 / 4
-
|
|
ЗлойБарсик ( Слушатель ) |
| 19 окт 2016 в 23:40 |
На самом деле, меньше. Вы считаете так, словно у вас самолет разбегается по горизонтальной полосе с вектором тяги, параллельным вектору скорости (по крайней мере, я не вижу в расчетах проекции вектора тяги на ось У). А для Су-33 важную роль играет именно эффект "подбрасывания" самолета трамплином и проекция вектора тяги на вертикальную ось. Ну, и плюс способность этого семейства сохранять устойчивость на очень малых значениях поступательной скорости. Вот это вместе дает возможность ещё уменьшить потребную скорость отрыва.
- +0.30 / 4
-
|
|
mirok ( Слушатель ) |
| 20 окт 2016 в 01:00 |
Приложил транспортир к фотке
получается на ровной взлетке угол атаки ограничен 10*, соответственно на трамплине будет макс. 24*, но при этом сопло будет уже чиркать по полосе. Так что 20* и запас 4* думаю правильно.
По поводу расчета, будь у меня все характеристики самолёта, я считал-бы так:
Систему координат привяжем к точке схода с трамплина, ось х направлена горизонтально по направлению движения, ось y вверх. Скорость ветра и авианосца не считаем, в принципе это равносильно просто увеличению начальной скорости по х в момент отрыва.
Обозначения постараюсь использовать одинаковые с расчетами уважаемого Artkonstruktor-а
по 2 закону Ньютона составим систему уравнений:
G*Ax=Rx;
G*Ay=Ry
где G - взлетная масса, Rx и Ry - проекции равноденствующей силы на оси, Ax=d2x/dt2 Ay=d2y/dt2 - проекции ускорения на оси, равные вторым производным координат.
Rx=Fтяги*cos(a)-Fсопр, где Fтяги - тяга двигателя, а - угол атаки. Считаем что вектором тяги летчик на взлёте не крутит и он направлен вдоль оси самолёта, а сила тяги не зависит от скорости (на самом деле думаю что зависит.) Fсопр - сила сопротивления набегающего потока воздуха - тут сложно, она зависит от скорости, т.е. от dx/dt и угла атаки. Если угол атаки считаем постоянным, то из переменных остается зависимость от dx/dt.
Ry=Fтяги*sin(a)-G*g+Fпод, где Fпод - подъемная сила, зависит от скорости, угла атаки и высоты, т.е из переменных там dx/dt и y
Из непонятного - формулы зависимостей Fпод(dx/dt,y) и Fсопр(dx/dt)
Зная начальные значения скорости, угла и тяги в момент отрыва можно было-бы довольно просто численно просчитать всю траекторию и поиграть массой, углом атаки и даже направлением вектора тяги для подбора оптимального алгоритма взлёта. Но я не представляю как и где найти эти зависимости. Да, кстати, т.к. тут у нас численный метод зависимости можно даже в виде таблиц применить, там легко апроксимировать.
Ничего я не пропустил?
- +0.06 / 2
-
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 23:45 |
Цитата: mirok от 19.10.2016 23:00:48
Ну вот видите, все просто.

Угол схода 14 градусов.
Тяга на форсаже – 2 х 13500 кгс
Масса 31000 кг
Скорость схода 170 км/ч
Творите.
Я правда, в свое время, запаривался по взрослому:
Цитата: ЦитатаИтак вводные данные.
Длина разбега 180 м
Длина трамплина 50 м. Высота 6,25 м. Трамплин представляет собой кривую описывающую уравнение у=0.0025х^2
Угол схода 14,0362 градуса.
Сперва делим всю длину разбега на 180 участков. Принимаем на каждом из них движение самолета как равноускоренное.
Расчитывая скорость по формуле V=V0 + at
Ускорение расчитываем по формуле ix = g*((P-X-F)/G)-g*sin a
Где g*sin a значение учитывающий потери ускорения при наклоне палубы.
По приращению функции находим противолежащий катет. Прилижащий нам известен (1м). Находим tg a и сам угол.
Принимая найденый угол за угол атаки высчитываем Су и Сх.
Получив эти данные Находим Y - подъемную силу. Х - лобовое сопротивление. F - силу трения колес.
Y=Cy*p*V2*S/2*g
X=Cx*p*V2*S/2*g
F=0,003*(G-Y)
Подставив полученные значения находим ускорение ix и конечную скорость на каждом участке V.
в любом случае будет интересно посмотреть ваш вариант.
Удачи.

- +0.02 / 1
-
|
|
mirok ( Слушатель ) |
| 20 окт 2016 в 23:57 |
О! супер! Часть вопросов снялось.
Но, осталось
Цитата: ЦитатаИз непонятного - формулы зависимостей Fпод(dx/dt,y) и Fсопр(dx/dt)
- +0.03 / 1
-
|
|
Н Н ( Слушатель ) |
| 20 окт 2016 в 05:57 |
из "Инструкции... Су-33":
Vотрыва с mвзл=25000 кг =140 км/ч
Vотрыва с mвзл=31000 кг = 170 км/ч
Vпосадки с mпос.max=22300 кг = 240 км/ч
- +0.10 / 4
-
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 10:38 |
Цитата: Н Н от 20.10.2016 03:57:51
А инструкцию можно глянуть, ну хоть одним глазком?

Vотр это на бетонке, или при сходе с трамплина?
Похоже, что второе.
Не могут скорости отрыва и посадки так кардинально отличаться.
- +0.00 / 0
-
|
|
ЗлойБарсик ( Слушатель ) |
| 20 окт 2016 в 14:44 |
Могут. Требования разные к этим режимам. На взлете двигатели в форсажном режиме работают, при достижении скорости отрыва можно поднимать машину от земли, скорость в любом случае будет расти - для их тяговооруженности даже на вертикали. А при посадке двигатели на минимуме, поэтому должен быть запас от скорости отрыва в целях безопасности. Мало ли что в последний момент на полосе может образоваться...
- +0.03 / 1
-
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 16:38 |
Если подъемная сила меньше массы самолета, то не сможет.
У Су-33 минимально допустимая скорость 200 км/ч.
По летным нормам скорость взлета должна быть больше на 20%, а посадки на 15%.
240 и 230 км/ч соответственно.
И форсаж тут не при чем.
- +0.03 / 1
-
|
|
Н Н ( Слушатель ) |
| 20 окт 2016 в 17:32 |
 Лучше картинки пароходиков рисуйте. У вас это лучше получается.
Лучше картинки пароходиков рисуйте. У вас это лучше получается.PS Не обижайтесь, но у вас жирная каша из цифр без понимания процесса.
- +0.00 / 0
-
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 19:33 |
Сообщение удалено
Artkonstruktor
20 окт 2016 в 23:46
Artkonstruktor
20 окт 2016 в 23:46
Отредактировано: Artkonstruktor - 20 окт 2016 в 23:46
|
|
Йохан Палыч ( Специалист ) |
| 20 окт 2016 в 20:51 |
Дружище! Не сердитесь на коллегу НН. Он иногда бывает резковат, что поделать, характер.

Вы исходите из цифр для Су-27, которые есть в открытом доступе, но для Су-33 они "чуть-чуть" другие.
Все расчеты, которые ходят по сети, очень приблизительные, но по большому счету - не имеют смысла. Все давно посчитано и испытано, и, соответственно, заложено в РЛЭ и облетано летчиками. Нормально с 3-ей позиции взлетает Су-33 с полной нагрузкой на форсаже, еще и с "запасом". Не делают этого в повседневной практике по простой причине: Су-33 - истребитель ПВО и выполняет задачи ПВО КУГ прежде всего. ПКР ему - как корове седло. Для выполнения этих задач он даже не рассматривается. Ударник на палубе - МиГ-29КР с "Х-семейством" для оперативного реагирования на возникающие с моря угрозы.
Ну, и не последнюю роль играет ресурс. Все-таки взлет-посадка с полной нагрузкой - серьезное испытание для планера, и, особенно - шасси. Зачем его интенсивно сокращать? Машин и так не много.
- +0.43 / 11
-
|
|
AbraKadabra ( Слушатель ) |
| 20 окт 2016 в 22:26 |
Сообщение удалено
Роман81
21 окт 2016 в 02:31
Роман81
21 окт 2016 в 02:31
Отредактировано: Роман81 - 21 окт 2016 в 02:31
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 22:48 |
Сообщение удалено
Artkonstruktor
20 окт 2016 в 22:48
Artkonstruktor
20 окт 2016 в 22:48
Отредактировано: Artkonstruktor - 20 окт 2016 в 22:48
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 22:59 |
Палычь

Твою дивизию... Я аж прослезился.
[movie=400,300]http://youtu.be/Zq0NMwkzRl8[/movie]
- +0.03 / 2
-
|
|
ЗлойБарсик ( Слушатель ) |
| 20 окт 2016 в 22:08 |
Минимально допустимая скорость в установившемся горизонтальном полете. Вы никогда не видели, как Су-27 летит на скорости чуть больше сотни в час с углом атаки градусов так под 45? Вот и форсаж при чем. При полёте с углом атаки проекция тяги на вертикальную ось позволяет компенсировать нехватку чисто аэродинамической подъёмной силы. На угле атаки 20 градусов почти 35 (!!!) процентов тяги действует вдоль оси У.
- +0.09 / 4
-
|
|
Artkonstruktor ( Слушатель ) |
| 21 окт 2016 в 02:08 |
Теперь я понял, почему мириканские палубные летчики называли прыжки с трамплина цирковым трюком.

- +0.07 / 3
-
|
|
Н Н ( Слушатель ) |
| 20 окт 2016 в 17:27 |
Можно. По предъявлению допуска.

Цифры - со слов летчика, летавшего на Су-33.
- +0.07 / 3
-
|
|
mse ( Специалист ) |
| 20 окт 2016 в 20:14 |
Цитата: Н Н от 20.10.2016 03:57:51
Ога... При массе пустого 19500, боевой нагрузке, условным БРАМОСом
 (2т), парой Р-77 (400кг) и парой Р-73(250кг), равной, примерно, 2700-3000кг, общая масса будет совсем округлённо, 23т. Льём 8т горючки и дозаправляемся до полных баков в воздухе. Нормально, чо!
(2т), парой Р-77 (400кг) и парой Р-73(250кг), равной, примерно, 2700-3000кг, общая масса будет совсем округлённо, 23т. Льём 8т горючки и дозаправляемся до полных баков в воздухе. Нормально, чо!
- +0.04 / 2
-
|
|
Йохан Палыч ( Специалист ) |
| 20 окт 2016 в 20:58 |
Цитата: mse от 20.10.2016 18:14:35
Хто о чём, а ... mse

Не будет "Ониксов" для Су-33. НЕ БУДЕТ. И для Т-50 (или что там на его базе слепят) - тоже не будет. Просто не нужен этот "цирк с конями" никому на палубе. Запишите себе в блокнотик и поставьте жирную-прежирную точку.
- +0.05 / 2
-
|
|
mse ( Специалист ) |
| 20 окт 2016 в 21:13 |
Я-ж говорю "условный".

Пару Х-35 каких, тоже хлеб. По массе, то на то.
- +0.03 / 1
-
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 23:24 |
Чистомо ИМХО, но с появлением "Цирконов" про штурмовку АУГ можно забыть.
- +0.01 / 1
-
|
|
Krechet ( Слушатель ) |
| 20 окт 2016 в 20:48 |
Цитата: Н Н от 20.10.2016 03:57:51
Артконструктор, Товарищ НН дело говорит...
Для взлета с трамплина не нужно 240, а вот при посадке на полном форсаже в момент касания палубы (что бы в случае обрыва троса или промаха на второй круг уйти с горизонтали) таки да, именно 240...
Помните, что для Т-10 и иже скорость в полете может быть и "0", смотря какая альфа...
- +0.21 / 5
-
|
|
Artkonstruktor ( Слушатель ) |
| 20 окт 2016 в 20:52 |
Сообщение удалено
Artkonstruktor
21 окт 2016 в 03:31
Artkonstruktor
21 окт 2016 в 03:31
Отредактировано: Artkonstruktor - 21 окт 2016 в 03:31