Конспирология и Эсхатология (на любителя)
5,227,121
3,523
|
|
mishinO5 ( Слушатель ) |
| 05 мар 2017 12:06:31 |
Тайна
новая дискуссия Дискуссия 487
Представьте себе такую "картину"... Акт первый: живущие на планете Земля разумные существа, глядя на небо, решили сделать шаг к познанию окружающего мира путем наблюдения ночью за небесными телами. Акт второй: один из наблюдателей предложил изучать небесные тела глядя на их отражение в воде. Аргумент простой: вниз легче смотреть, чем вверх. На том и порешили.
Теперь другая "картина", аналогичная первой, но уже не из области астрономии, а из области математики. Акт первый: живущие на планете Земля разумные существа, глядя по сторонам, решили сделать шаг к познанию окружающего мира путем вычерчивания геометрических фигур и выяснения численных соотношений между ними. Акт второй: один из вычисляющих эти закономерности предложил численные характеристики изображать в виде точек на числовой прямой. Аргумент простой: лучше абстрактно упростить, чем усложнять. На том и порешили.
Астрономам повезло, они не пошли по пути упрощения. Физикам и химикам тоже повезло. Они тоже пошли по пути усложнения, а не по пути упрощения... Математикам не повезло больше других...
Чем же так не повезло математикам?! Показываю на простом и очень наглядном примере. Для пущей наглядности будем сравнивать действия гипотетического астронома-фальсификатора, предложившего изучать небесные тела по их отражению в воде и действия гипотетического математика-фальсификатора, предложившего рассматривать все численные величины абстрактно.
Что такое: абстрактно? В двух словах: абстрагирование - это создание вымышленного ассоциативного ряда на основе одной или нескольких вычлененных характеристик объекта или ряда объектов которые, с учетом остальных характеристик, не поддаются уподоблению. Показываю на пальцах: если АБСТРАКТНО отложить в отрезках числовой оси возраст одного человека, равный 120 месяцам, вес другого, равный 120 килограммов и рост третьего, равный 120 сантиметров, то абстрактно эти три человека, УСЛОВНО, будут изображены в виде числовых отрезков равной длины. Но это изображение будет условным и никакого отношения к реальности иметь не будет! Не говоря уже о том, что если пересчитать рост в дюймах, вес в фунтах, а возраст в сутках, то даже о равенстве условно выбранных численных характеристик этих трех человек речи быть не может! То есть, абстрактности бывают только в иллюзиях, но никогда не бывают в действительности!
То есть, если дети играют в "войнушку" и один из них решает "быть Наполеоном", то это - детская шалость, а если взрослый человек решает "быть Наполеоном", то это - тяжелое психическое расстройство! Точно так же и в математике. Если Вы "условно" решили изобразить окружность в виде точки, а круг в виде прямой линии, то это - абстрактное условное ГРАФИЧЕСКОЕ изображение и не имеет никакого отношения кГЕОМЕТРИИ, то есть к науке! Но если кто-то называет условное графическое наглядное изображение геометрией, то это - тяжелое психическое расстройство. А если этому бреду придают научность и заставляют изучать в обязательной учебной программе - то это геноцид и преступление по отношению к человечеству!!!
Итак, от философских размышлений перейдем к практическому опыту. Для начала, нам надо четко отделить понятия линейной "диаграммы", "пространственной линейной системы координат" от понятия "график функции в Декартовой системе координат". В чем различие? В том, что вычерчивая, например, зависимость изменения температуры больного от времени измерения в виде линейной диаграммы или, например, траекторию полета артиллерийского снаряда в пространственной системе координат, Вы сопоставляете ПОЛУЧЕННЫЕ значения величин. Потому, что сами координаты заранее не известны и зависят от самочувствия больного в данный момент времени или от наличия ветра, заряда пороха или нагрева ствола в данный момент времени и НЕ МОЖЕТ БЫТЬ ТОЧНО ВЫЧИСЛЕНО ЗАРАНЕЕ. То есть, значения, откладываемые по осям координат независимы друг от друга и откладываются ПО ФАКТУ.
В Декартовой системе координат значения, откладываемые по осям координат зависимы: y=f(x). Поэтому начертание произвольной линии в Декартовой системе координат - признак некомпетентности или психического расстройства! Смотреть здесь по пятой по счету ссылке.
Если рассмотреть две функции отрезка переменной длины, называемого в геометрии радиусом: "длину окружности" и "площадь круга", то эти две функции одного и того же аргумента (радиуса) будут иметь между собой специфическую связь, как "производная" и "первообразная". Подробно: здесь и здесь.
Ну, а теперь самое главное! Та самая ТАЙНА, которую я собираюсь Вам поведать. Допустим, мы решили начертить график функции площади круга. ЧТО ИМЕННО МЫ ПОЛУЧИМ В УСЛОВНОМ ИЗОБРАЖЕНИИ В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ В ВИДЕ ГРАФИЧЕСКИХ УСЛОВНЫХ ОБЪЕКТОВ?
То есть, с точки зрения астрономии, как соотносятся изображения небесных объектов и их траектории движения с точки зрения астронома-фальсификатора, рассматривающего отражение неба в воде, с точкой зрения реального астронома, рассматривающего эти же объекты и эти же траектории движения, в реальном небе?
В математике это будет выглядеть так. С точки зрения математика-фальсификатора нет никакой разницы в изображении значений переменной площади круга в виде реальных геометрических фигур и в изображении этих же значений на числовой оси ординат в Декартовой системе координат.
Мы же с Вами, как реалисты, которым в средней школе, на уроках математики, пытались "сломать мозг" попробуем стряхнуть "лапшу с ушей" и глянем на проблему незамутненным шизофреническими иллюзиями взглядом. То есть возьмем себя в руки и попытаемся понять, чем все-таки отличается фраза: "ветер дует от того, что деревья качаются" от фразы: "деревья качаются от того, что дует ветер"...
Никто не спорит с тем, что изображение "графика функции" полезно для НАГЛЯДНОСТИ. Но, эту наглядность, которая не имеет никакого отношения к научному знанию математики-фальсификаторы использовали для того, чтобы ОДУРАЧИТЬ ЛЮДЕЙ ВСЕГО ЗЕМНОГО ШАРА, объявив о доказательстве самой величайшей математической проблемы, которая, на самом деле КРИЧИТ о том, что в некоторых разделах математики есть НЕВЕРНЫЕ ВЫВОДЫ!!!
Желательно, изучая расположение и движение небесных тел по отражению их в воде, хотя бы изредка поднимать голову вверх, чтобы сравнитьПРАВИЛА, полученные путем изучения этих иллюзорных воображаемых абстрактных объектов с поведением их реальных "аналогов", которые существуют в реальном мире.
Сравните сами две фразы: "Производная площади круга по радиусу - есть длина описанной вокруг круга окружности". "Первообразная длины окружности по радиусу - есть площадь вписанного круга" с этим:
"...Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции в точке
в точке 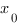 равен производной функции
равен производной функции  в этой точке..."
в этой точке..."
Совершенно очевидно человеку с незамутненным рассудком, что если по вертикали в Декартовой системе координат "откладывать" значения переменной площади круга, то значения длин описывающих соответствующие круги окружностей будут численно равны значениям тангенсов углов наклона касательных, проведенных к кривой в соответствующих точках. Но!!! Не "ТАНГЕНС... равен ПРОИЗВОДНОЙ в ... точке", аДЛИНЫ ОКРУЖНОСТЕЙ, являющиеся значениями производной, можно использовать для начертания прямых, имеющих одну общую точку с "кривой" . То есть, не хвост виляет собакой, а собака хвостом!!!
То есть, угловой коэффициент наклона касательной не является геометрическим смыслом производной! Так как угол, в данном рассматриваемом случае, не является аналогом длины окружности. Равенство двух чисел: значения тангенса угла и значение длины окружности не имеет никакого иного смысла, как только равенство двух чисел, не имеющих никакой геометрической связи!

Источник: http://mishin05.live…75891.html
Теперь другая "картина", аналогичная первой, но уже не из области астрономии, а из области математики. Акт первый: живущие на планете Земля разумные существа, глядя по сторонам, решили сделать шаг к познанию окружающего мира путем вычерчивания геометрических фигур и выяснения численных соотношений между ними. Акт второй: один из вычисляющих эти закономерности предложил численные характеристики изображать в виде точек на числовой прямой. Аргумент простой: лучше абстрактно упростить, чем усложнять. На том и порешили.
Астрономам повезло, они не пошли по пути упрощения. Физикам и химикам тоже повезло. Они тоже пошли по пути усложнения, а не по пути упрощения... Математикам не повезло больше других...
Чем же так не повезло математикам?! Показываю на простом и очень наглядном примере. Для пущей наглядности будем сравнивать действия гипотетического астронома-фальсификатора, предложившего изучать небесные тела по их отражению в воде и действия гипотетического математика-фальсификатора, предложившего рассматривать все численные величины абстрактно.
Что такое: абстрактно? В двух словах: абстрагирование - это создание вымышленного ассоциативного ряда на основе одной или нескольких вычлененных характеристик объекта или ряда объектов которые, с учетом остальных характеристик, не поддаются уподоблению. Показываю на пальцах: если АБСТРАКТНО отложить в отрезках числовой оси возраст одного человека, равный 120 месяцам, вес другого, равный 120 килограммов и рост третьего, равный 120 сантиметров, то абстрактно эти три человека, УСЛОВНО, будут изображены в виде числовых отрезков равной длины. Но это изображение будет условным и никакого отношения к реальности иметь не будет! Не говоря уже о том, что если пересчитать рост в дюймах, вес в фунтах, а возраст в сутках, то даже о равенстве условно выбранных численных характеристик этих трех человек речи быть не может! То есть, абстрактности бывают только в иллюзиях, но никогда не бывают в действительности!
То есть, если дети играют в "войнушку" и один из них решает "быть Наполеоном", то это - детская шалость, а если взрослый человек решает "быть Наполеоном", то это - тяжелое психическое расстройство! Точно так же и в математике. Если Вы "условно" решили изобразить окружность в виде точки, а круг в виде прямой линии, то это - абстрактное условное ГРАФИЧЕСКОЕ изображение и не имеет никакого отношения кГЕОМЕТРИИ, то есть к науке! Но если кто-то называет условное графическое наглядное изображение геометрией, то это - тяжелое психическое расстройство. А если этому бреду придают научность и заставляют изучать в обязательной учебной программе - то это геноцид и преступление по отношению к человечеству!!!
Итак, от философских размышлений перейдем к практическому опыту. Для начала, нам надо четко отделить понятия линейной "диаграммы", "пространственной линейной системы координат" от понятия "график функции в Декартовой системе координат". В чем различие? В том, что вычерчивая, например, зависимость изменения температуры больного от времени измерения в виде линейной диаграммы или, например, траекторию полета артиллерийского снаряда в пространственной системе координат, Вы сопоставляете ПОЛУЧЕННЫЕ значения величин. Потому, что сами координаты заранее не известны и зависят от самочувствия больного в данный момент времени или от наличия ветра, заряда пороха или нагрева ствола в данный момент времени и НЕ МОЖЕТ БЫТЬ ТОЧНО ВЫЧИСЛЕНО ЗАРАНЕЕ. То есть, значения, откладываемые по осям координат независимы друг от друга и откладываются ПО ФАКТУ.
В Декартовой системе координат значения, откладываемые по осям координат зависимы: y=f(x). Поэтому начертание произвольной линии в Декартовой системе координат - признак некомпетентности или психического расстройства! Смотреть здесь по пятой по счету ссылке.
Если рассмотреть две функции отрезка переменной длины, называемого в геометрии радиусом: "длину окружности" и "площадь круга", то эти две функции одного и того же аргумента (радиуса) будут иметь между собой специфическую связь, как "производная" и "первообразная". Подробно: здесь и здесь.
Ну, а теперь самое главное! Та самая ТАЙНА, которую я собираюсь Вам поведать. Допустим, мы решили начертить график функции площади круга. ЧТО ИМЕННО МЫ ПОЛУЧИМ В УСЛОВНОМ ИЗОБРАЖЕНИИ В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ В ВИДЕ ГРАФИЧЕСКИХ УСЛОВНЫХ ОБЪЕКТОВ?
То есть, с точки зрения астрономии, как соотносятся изображения небесных объектов и их траектории движения с точки зрения астронома-фальсификатора, рассматривающего отражение неба в воде, с точкой зрения реального астронома, рассматривающего эти же объекты и эти же траектории движения, в реальном небе?
В математике это будет выглядеть так. С точки зрения математика-фальсификатора нет никакой разницы в изображении значений переменной площади круга в виде реальных геометрических фигур и в изображении этих же значений на числовой оси ординат в Декартовой системе координат.
Мы же с Вами, как реалисты, которым в средней школе, на уроках математики, пытались "сломать мозг" попробуем стряхнуть "лапшу с ушей" и глянем на проблему незамутненным шизофреническими иллюзиями взглядом. То есть возьмем себя в руки и попытаемся понять, чем все-таки отличается фраза: "ветер дует от того, что деревья качаются" от фразы: "деревья качаются от того, что дует ветер"...
Никто не спорит с тем, что изображение "графика функции" полезно для НАГЛЯДНОСТИ. Но, эту наглядность, которая не имеет никакого отношения к научному знанию математики-фальсификаторы использовали для того, чтобы ОДУРАЧИТЬ ЛЮДЕЙ ВСЕГО ЗЕМНОГО ШАРА, объявив о доказательстве самой величайшей математической проблемы, которая, на самом деле КРИЧИТ о том, что в некоторых разделах математики есть НЕВЕРНЫЕ ВЫВОДЫ!!!
Желательно, изучая расположение и движение небесных тел по отражению их в воде, хотя бы изредка поднимать голову вверх, чтобы сравнитьПРАВИЛА, полученные путем изучения этих иллюзорных воображаемых абстрактных объектов с поведением их реальных "аналогов", которые существуют в реальном мире.
Сравните сами две фразы: "Производная площади круга по радиусу - есть длина описанной вокруг круга окружности". "Первообразная длины окружности по радиусу - есть площадь вписанного круга" с этим:
"...Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции
Совершенно очевидно человеку с незамутненным рассудком, что если по вертикали в Декартовой системе координат "откладывать" значения переменной площади круга, то значения длин описывающих соответствующие круги окружностей будут численно равны значениям тангенсов углов наклона касательных, проведенных к кривой в соответствующих точках. Но!!! Не "ТАНГЕНС... равен ПРОИЗВОДНОЙ в ... точке", аДЛИНЫ ОКРУЖНОСТЕЙ, являющиеся значениями производной, можно использовать для начертания прямых, имеющих одну общую точку с "кривой" . То есть, не хвост виляет собакой, а собака хвостом!!!
То есть, угловой коэффициент наклона касательной не является геометрическим смыслом производной! Так как угол, в данном рассматриваемом случае, не является аналогом длины окружности. Равенство двух чисел: значения тангенса угла и значение длины окружности не имеет никакого иного смысла, как только равенство двух чисел, не имеющих никакой геометрической связи!

Источник: http://mishin05.live…75891.html
ОТВЕТЫ (4)
|
|
mishinO5 ( Слушатель ) |
| 05 мар 2017 20:36:40 |
Цитата: slavae от 05.03.2017 15:11:00
Это в смысле просто вонючий высер или есть какая-нибудь доказательная аргументация?
|
|
Zkvxz ( Слушатель ) |
| 05 мар 2017 18:41:30 |
Сообщение удалено
Zkvxz
06 мар 2017 00:30:56
Zkvxz
06 мар 2017 00:30:56
Отредактировано: Zkvxz - 06 мар 2017 00:30:56
|
|
mishinO5 ( Слушатель ) |
| 05 мар 2017 20:38:36 |
Цитата: Zkvxz от 05.03.2017 18:41:30
Картинка не вписалась в размер мозга или еще какое-нибудь неудобство?
