Температура фотокамеры на Луне
20 дек 2018 в 13:32
ILPetr
|
|---|
|
Добрый день, на соседней ветке не стихает истерика про жуткий нагрев фотокамеры на лунной поверхности, я тут "карандашиком по салфетке" прикинул температуру Хасселя на Луне.
Примем в качестве исходных следующие данные: 1. размеры фотокамеры 10х10х20 см, объектив цилиндрический диаметром 7 см и длиной 10 см; 2. солнечная постоянная 1367 Вт/м2; 3. альбедо лунного грунта 0,1; 4. температура грунта 300 К. Определяем общую площадь поверхности фотокамеры: 4 х 0,2 х 0,1 + 2 х 0,1 х 0,1 + 3,14 х 0,07 х 0,1 = 0,122 м2. Первое слагаемое это площадь боковых стенок камеры с присоединенной кассетой пленки, второе – передний и задний торцы, третье – площадь цилиндрической обечайки объектива. «Линза» объектива отдельно не считалась и учтена в площади переднего торца камеры. Зачем мы ее посчитали – это площадь, излучение которой охлаждает фотокамеру. Посчитаем поверхность, которая будет освещаться Солнцем или другими источниками и нагревать камеру. Для этого возьмем один из самых тяжелых режимов, когда Солнце равномерно освещает две боковые стенки камеры, т.е. считаем по площади диагонального сечения «бруска» камеры и продольного сечения объектива: √2 х 0,1 х 0,2 + 0,07 х 0,1 = 0,0291 м2. Не забудем, что примерно половина общей площади фотокамеры будет «нагреваться» излучением лунного грунта. Это излучение будет состоять из непосредственно отраженного солнечного света, 10% от падающего и теплового излучения самого грунта, которое мы можем посчитать по закону Стефана-Больцмана: S = σT4 Где S – энергетическая светимость, T – температура в кельвинах, а σ – постоянная Больцмана, равная 5,67 х 10-8 Вт / (м2 · К4) 5,67 х 10-8 х 3004 = 459 Вт/м2. Нагреваться-то лунным излучением будет примерно половина камеры, и даже больше половины, но считать конкретное распределение потоков по стенкам мы не будем, а опять же возьмем площадь диагонального сечения и светимость грунта. Итак, наша фотокамера будет получать в виде солнечного, отраженного грунтом и теплового излучения грунта: 0,0291 (1367 + 0,1 х 1367 + 459) = 57,1 Вт. Первый множитель это площадь диагонального сечения камеры, слагаемые в скобках: солнечная постоянная, отраженный грунтом солнечный поток и тепловое излучение грунта. Нас интересует установившаяся температура при которой фотокамера будет излучать в пространство точно такое же количество энергии. Для этого берем тот же закон Стефана-Больцмана и считаем по нему «подставив» наши значения излучаемой мощности и общей площади поверхности нашей фотокамеры: T = 4√ (S/σ) = 4√ (57,1 / (0,122 х 5,67 х 10-8)) = 301 К или +28°С. (57,1 / 0,122 в формуле - это пересчет мощности излучения на квадратный метр.) Собственно, это оценка максимальной температуры, до которой может быть нагрет фотоаппарат, на практике фотоаппарат попадал и в солнечную тень и астронавт своим скафандром экранировал фотоаппарат от части теплового и отраженного излучения грунта. Можно посчитать и минимальную температуру фотокамеры в лунной тени, но, ПМСМ, время нахождения в тени было пренебрежимо малым и камера не имела возможности остыть до таких температур. О цвете фотокамеры. Весь расчет сделан из предположения об абсолютно черном теле, что кажется абсурдным для фотокамеры, корпус которой выкрашен в светлый серебристый цвет. Однако я считал "стационарный" процесс для равновесной температуры, достигаемой в результате достижения баланса поглощаемой и излучаемой мощностей. Если мы подставим коэффициент черноты в этот баланс, то этот коэффициент будет в обеих частях - он будет влиять и на поглощение и на излучение, и чисто с точки зрения математики может быть сокращен.  Но интересен момент влияния этого коэффициента на скорость изменения температуры - она будет тем меньше, чем белее тело. Скорость изменения температуры оценить достаточно просто, например, оценим скорость охлаждения фотокамеры считая, что она абсолютно черная, изготовлена из алюминия (900 Дж/(кг·град) теплоемкость), имеет массу 2 кг. При заходе в тень поглощаемый камерой поток сократится на величину солнечной постоянной, при этом излучение от лунного грунта сохранится, т.е. поглощаемый поток уменьшится на: Но интересен момент влияния этого коэффициента на скорость изменения температуры - она будет тем меньше, чем белее тело. Скорость изменения температуры оценить достаточно просто, например, оценим скорость охлаждения фотокамеры считая, что она абсолютно черная, изготовлена из алюминия (900 Дж/(кг·град) теплоемкость), имеет массу 2 кг. При заходе в тень поглощаемый камерой поток сократится на величину солнечной постоянной, при этом излучение от лунного грунта сохранится, т.е. поглощаемый поток уменьшится на:0,0291 х 1367 = 40 Вт или Дж/с. Излучаемый же сохранится, поскольку температура еще не изменилась или изменилась пренебрежимо мало. Вот этот дефицит в 40 Дж/с и будет приводить к снижению температуры. (А если выйдем из тени, то именно эта разница и будет нагревать фотокамеру, повышать ее температуру.) Посчитаем скорость изменения температуры: 40 / (2 х 900) = 0,02 град/с или 1,2 град/мин. Это уже само говорит о том, что зайдя в тень минут на 10 о температуре камеры беспокоиться не стоит - камера остынет не более чем на 12 градусов. Если же мы покрасим камеру так, что она будет отражать 80% падающего потока и поглощать всего 20% (соответственно и излучать она будет в пять раз меньше абсолютно черной), то скорость нагрева/охлаждения станет в пять раз меньше, уже не 1,2 градуса в минуту, а всего 0,24 и на проблему переохлаждения в тени можно наплевать. 
Отредактировано: ILPetr - 20 дек 2018 в 13:32
|
|
Следующая дискуссия:
Событием года назвали проект строительства глубоководного порта в Пионерском >> |
ОТВЕТЫ (5)
|
|
normalized_ ( Слушатель ) |
| 20 дек 2018 в 14:18 |
Цитата: ILPetr от 20.12.2018 13:32:08
А вот в этом сомневаюсь.

1) Коэффициент черноты - это отношение потока тела на поток АБЧ нагретому до той-же температуры.
2) Поэтому нужно учесть что спектры падающего (солнечного 6000К, максимум плотности энергии в видимом цвете) и излучающего (600 К, максимум плотности энергии в инфракрасном диапазоне, по закону Вина и Планка) разные, и коэффициенты поглощения и излучения могут для них отличаться.
Иными словами при применении Стефана-Больцмана (а она есть интеграл от формулы Планка) из за разных форм спектра интеграл получится разный.
3) Поэтому при вычислении равновесной температуры или эффективной температуры для планет, например, белого листа (или снег) по сравнению с черным нужно учитывать различие коэффициентов поглощения и излучения для разных длин волн (в инфакрасном диапазоне снего очень-очень черный). В солнечном спектре "белые" материалы много отражают, но в инфракрасном диапазоне коэффициент излучения близок к 1 (в этом диапазоне они казались бы "черными").
И вот только если тело нагреется до температуры источника (например до 6000 градусов) то его коэффициенты поглощения и излучения сравняются.
P.S.
Перегрев: Про фотоаппараты на Луне (Луноход)
P.P.S. Самое забавное, что:
- во время миссий ТВ камера Apollo-15 из-за высокого солнца в конце третьего выхода, перестала держать высоты, из-за перегрева детали (пластмассовой, в последующих миссиях ее заменили).
- Даже в описании миссии, говорится о нескольких случаях, когда пленка не проматывалась (отказ кассеты).
я уже не говорю о нескольких фотографиях с низким качеством, обычно в конце кассеты-магазина.
Впрочем, если положить телефон или пленочный фотик на солнце в ясный день, то он тоже может перегреться, особенно если он черный (или заморозиться зимой). А зажигалка вообще может взорваться.
Но чехлы используют не белые (против солнца), а для переноски, чтоб не "покоцать" технику купленную не на один день, а на года.
- +0.20 / 10
-
|
|
ILPetr ( Слушатель ) |
| 20 дек 2018 в 14:47 |
Да, безусловно. Но мы (я) спектральных характеристик не знаем, поэтому в моей оценке они не учтены и тело черное, т.е. с постоянным коэффициентом черноты, не зависящем от длины волны. Можно поиграться, но зачем? Если АЧТ обеспечивает комфортные условия.
Пленка не проматывалась, ПМСМ, из-за нарушения плотности намотки - на фабрике могли мотать плотно-плотно, поскольку не были ограничены мощностью привода, а в камере первые кадры наматывались на голый вал, а последние - на рулон использованной пленки. При механизме перемотки с постоянным крутящим моментом первые кадры будут мотаться плотнее последних, это вызовет недопустимое увеличение диаметра рулона пленки и его контакт со стенками кассеты, т.е. дополнительное сопротивление, что будет дополнительно тормозить, и на последние просто может не хватить "тяги".
- +0.17 / 9
-
|
|
Alexxey ( Слушатель ) |
| 20 дек 2018 в 16:45 |
Сама камера, однако, никаких проблем в работе не испытывала. Тут полезно пояснить, что же там случилось с камерой А15, вернее, с её "турелью" GCTA (Ground-Commanded Television Assembly) — хреновиной, с помощью которой камеру можно было вертеть по командам с Земли по азимуту и углу места:

Помимо верчения по командам с Земли, необходимо было обеспечить возможность перенаправлять камеру астронавтами — грубо говоря, в любой момент подойти и направить по нужным азимуту и углу места просто вручную. После такого ручного вмешательства оператор на Земле, если нужно было, крутил камеру в крайние положения, чтобы "обнулиться". Так вот, такая возможность ручного управления обеспечивалась нежёсткой связью валов вращения камеры с управляющими шестернями приводов. Вращение камеры было выполнено проскальзывающим, через подпружиненное уплотнение с определённым расчётным усилием проскальзывания, комфортным для ручного перенаправления, но достаточно сильным для того, чтобы камера не "клевала" под собственным весом. Вот с пластмассовой деталью этого уплотнения и просчитались. Рассчитанное на рабочую температуру до 45°, уже во время EVA-2 оно начало барахлить при остановках ровера на длительные периоды по 20-30 минут узлом управления по углу места к Солнцу. А к концу EVA-3 этот узел уже стал регулярно проскальзывать под весом камеры — она начала "клевать". Из-за этого дефекта взлёт А15 с Луны снят так, как он снят. (В голливуде такого не придумывают, кстати. Как и в случае с аварией А13 — когда разбираешься до технических тонкостей произошедшего, вывод напрашивается сам собой: ну ни один, сука, сценарист такого выдумать просто не в состоянии, такой треш бывает только в жизни.
 ) Ну а в А16/17 опыт был учтён и соответствующие модификации внесены.
) Ну а в А16/17 опыт был учтён и соответствующие модификации внесены.
- +0.17 / 10
-
|
|
normalized_ ( Слушатель ) |
| 25 дек 2018 в 15:47 |
Цитата: ILPetr от 20.12.2018 13:32:08
Там ДальнийВ давеча упомянул про скафандры ("Поищите это - Spacesuits.djvu, Мои ссылки битые.")
Нашел:
Алексеев С.М., Уманский С.П. Высотные и космические скафандры 1973 г. (страница 225)
http://epizodsspace.airbase.ru/bibl/alekseev-s/vysotnye/01.html (djvu 13,6 Мб)
На странице 224 там в главе "Теплообмен между космонавтом и окружающей средой в условиях лунной поверхности" делается расчет на примере скафандра.

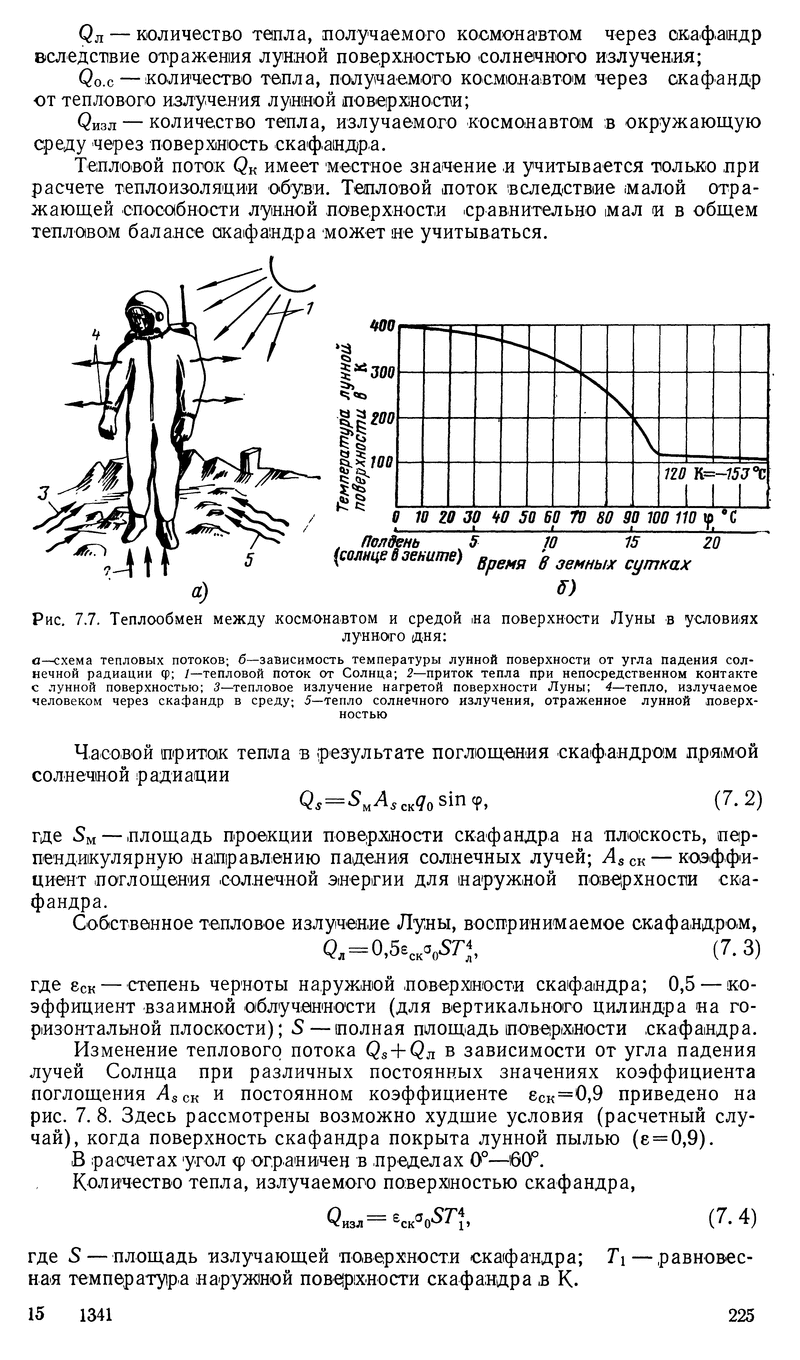
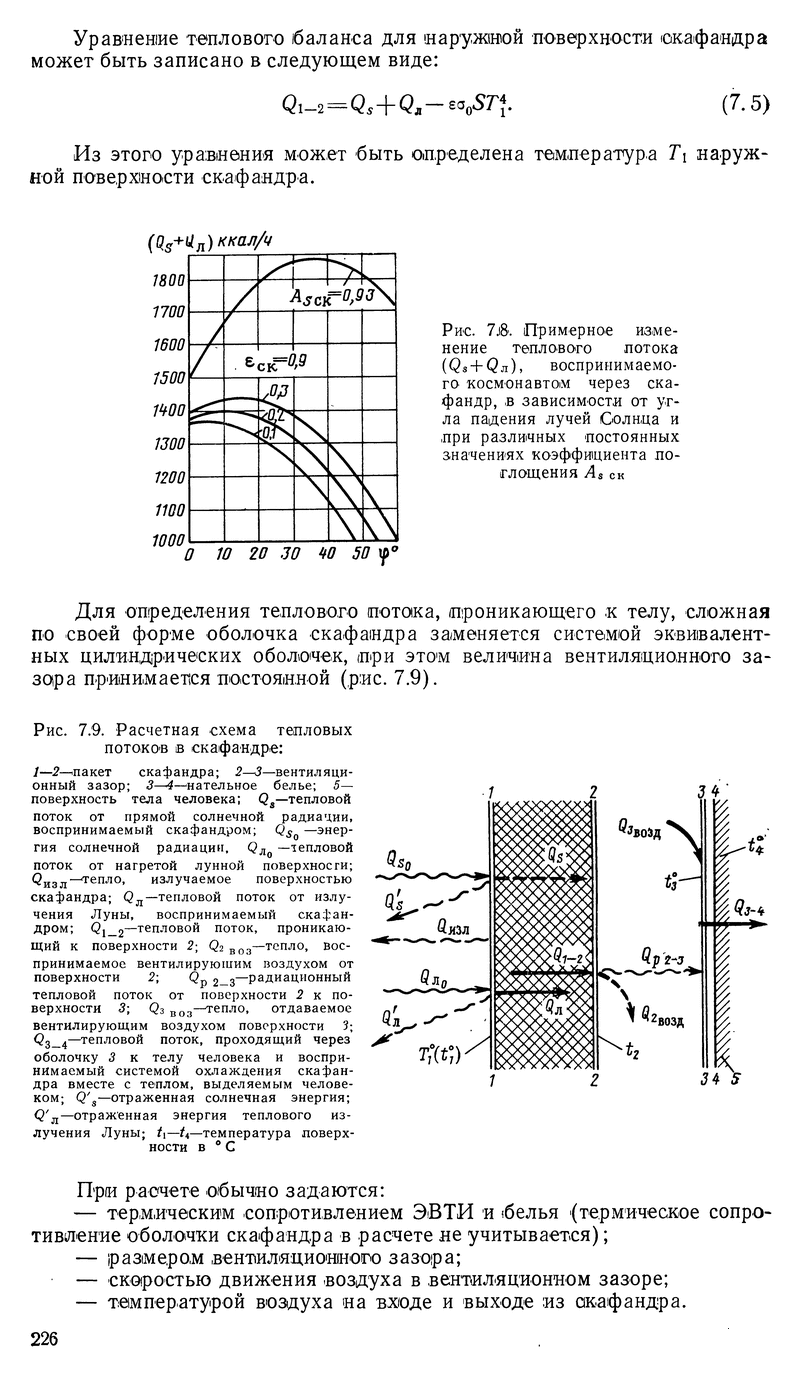
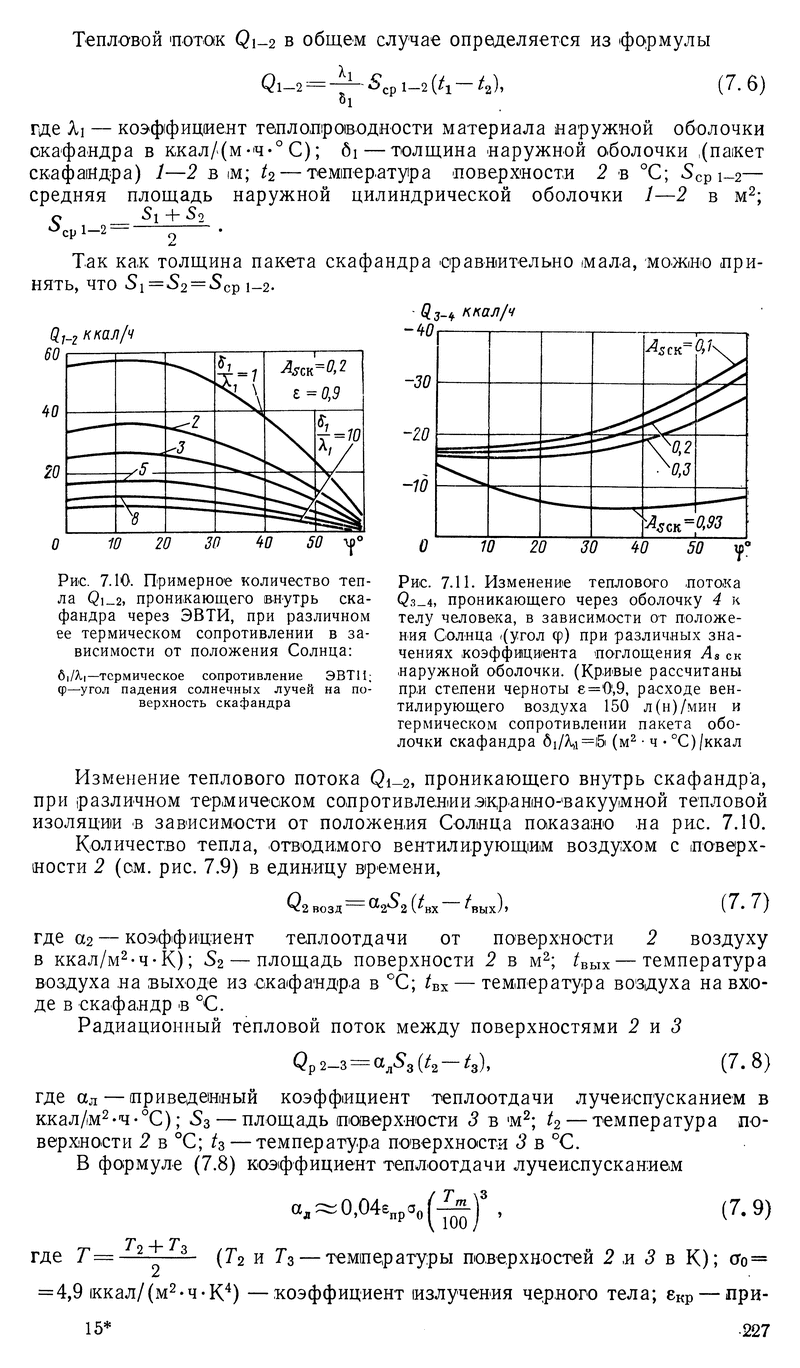
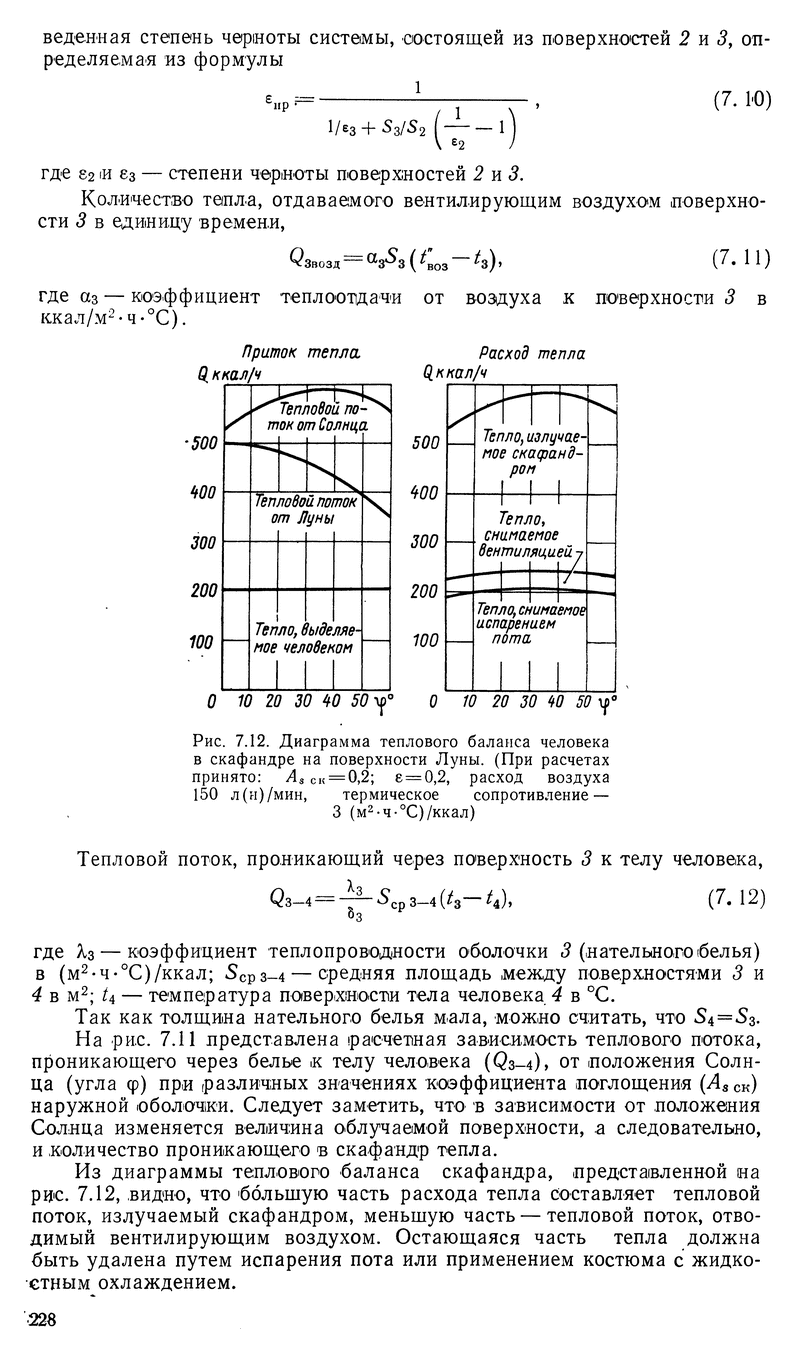
- +0.19 / 11
-