Тред №315997
12 апр 2011 в 10:31
Yuri Rus
|
|---|
|
Я думаю, теперь легко понять, почему ранее упомянутый аргумент из книги Leigh Page ”Introduction to Theoretical Physics” неверен. Приведу эту цитату еще раз:
  (я с удовольствием заменю это на русский текст, если мне дадут ссылку на подходящую книгу) Здесь, на самом деле, много ошибок (прежде всего, в уравнении полностью отсутствует источник и какой-либо намек на его движение), но я их касаться сейчас не буду . Позже я именно об этом буду много говорить. Главным для меня сейчас является вот такой аргумент: Если электрический заряд двигается по оси х, напряженность электрического поля Е в точке (x + vdt, y, z) в момент времени t + dt должна быть такой же, как в точке (x, y, z) в момент t, то есть E(x + vdt, y, z, t + dt) = E(x, y, z, t) В то же время, левый член, в соответствии с принятым в физике определением полного дифференциала (не моим определением, разумеется) можно разложить на E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt Отсюда получается ∂E/∂t = – v (∂E/∂x) Повторив эту математическую манипуляцию еще раз, получаем ∂₂E/∂t₂ = v₂ (∂₂E/∂x₂) а также (1 – β₂)(∂₂E/∂x₂) + ∂₂E/∂y₂ + ∂₂E/∂z₂ = 0 Я даже не буду останавливаться на том, что после этих математических манипуляций трехмерное волновое уравнение со скоростью распространения волн c трансформировалось в одномерное волновое уравнение со скоростью распространения волн v и в уравнение Лапласа со «сплющенной» координатой х, что не имеет никакого физического смысла. Меня здесь интересует только это уравнение: E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt Предположительно, это уравнение следует из определения «классического» полного дифференциала: dE = (∂E/∂x)dx + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)dt Полагая dx = vdt, dy = 0, dz = 0, dt = dt, автор и получил вышеприведенное уравнение. Однако мы же теперь вооружены всесильным, потому что верным, определением полного дифференциала DЕ как: DE(x, y, z, ξ, t, ԏ) = (∂E/∂x)(dx – dξ) + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)(dt – dԏ) Благодаря этому определению, мы сразу видим, что вместо E(x, y, z, t) и E(x + vdt, y, z, t + dt) следует использовать E(x, y, z, ξ, t, ԏ) и E(x + vdt, y, z, ξ + vdt, t + dt, ԏ + dt). Необходимо, таким образом, учитывать не только dx = vdt, dy = 0, dz = 0, dt = dt, но и dξ = vdt и dԏ = dt. И поскольку dx = dξ и dt = dԏ (а также dy = 0, dz = 0), то при переходе от точки (x, y, z, ξ, t, ԏ) к точке (x + vdt, y, z, ξ + vdt, t + dt, ԏ + dt), как (∂E/∂x)(dx – dξ), так и (∂E/∂t)(dt – dԏ) равны 0. Никакого равенства ∂E/∂t = – v (∂E/∂x) нет, а следовательно, нет и никакого сжатия по оси х. В рамках предлагаемой теории, «классический» полный дифференциал на самом деле является всего лишь единичным дифференциалом. Он имеет смысл только для фиксированных значений ξ и ԏ: dE(x, y, z, ξс, t, ԏс) = (∂E/∂x)dx + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)dt , то есть только для единичной волны, испущенной в точке (ξс, 0, 0) в момент времени ԏс. Как уже говорилось выше, при увеличении t на dt, волна эта перемещается на расстояние cdt, причем x, y и z изменятся одновременно и пропорционально скорости распространения волны c (а не скорости источника v): dx = cdt cos α dy = cdt cos β dz = cdt cos γ Таким образом, в момент t + dt эта единичная волна из точки (x, y, z) сместится в точку (x + cdt cos α, y + cdt cos β, z + cdt cos γ). Что касается E(x, y, z, t) и E(x + vdt, y, z, t + dt), то очевидно, что они принадлежат разным единичным волнам, разным единичным функциям. Уравнение же E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt не имеет ни физического, ни математического смысла. Я уделил так много внимания этому уравнению, потому что в нем в наиболее ясной и простой форме выражена типичная ошибка математической физики: полный дифференциал не включает частных производных по координатам движущегося источника как независимым переменным, и вообще движение источника никак не отражается в волновом уравнении. Кроме того, вышеприведенный аргумент с выведением (1 – β₂)(∂₂E/∂x₂) + ∂₂E/∂y₂ + ∂₂E/∂z₂ = 0 исторически сыграл важную роль в признании преобразований Лоренца и теории относительности, поскольку здесь в рамках вроде бы совершенно классической электродинамики и векторного анализа получается «сжатие» поля частицы в направлении ее движения. Я хотел показать, что этот аргумент неверен – вследствие неверного понимания, что такое полный дифференциал функции. Далее, очевидно, что полная функция f(x, y, z, ξ, η, ζ, t, ԏ) будет описывать волны только от одного движущегося источника. Если источников два, то взаимодействующие волны от этих источников потребуют введения не 4-х дополнительных координат ξ, η, ζ, ԏ, но 8-ми координат: ξ₁, η₁, ζ₁, ԏ₁, ξ₂, η₂, ζ₂, ԏ₂. Для n движущихся источников, потребуются уже 4n дополнительных координат: ξ₁, η₁, ζ₁, ԏ₁, ξ₂, η₂, ζ₂, ԏ₂ … ξn, ηn, ζn, ԏn. Аналогично изменится и полный дифференциал этой полной функции. Позже мы вернемся к этому вопросу. в частности, пересмотрим основные положения векторного анализа. Отредактировано: Yuri Rus - 21 ноя 2019 в 00:23
|
|
|
ОТВЕТЫ (4)
|
|
Поверонов ( Слушатель ) |
| 13 апр 2011 в 00:07 |
- ...
Цитата: Yuri Rus от 12.04.2011 10:31:01
Подход несомненно интересный, и уже с нетерпением жду продолжения.
Однако физика данного противопоставления осталась неясной.
В приведенном тексте на английском речь идет о статическом электрическом поле, хотя и с движущимся источником ( зарядом ).
Вы же рассматриваете поле f скорее как мгновенное излучение источником некоторой сферической волны.
Конечно, в физике давно уже практически отождествились статическое поле и электромагнитное излучение в концепции фотонов, но это так сказать в другой "квантовой" модели.
Здесь же рассматривается вполне классическое "дифференциальное" описание, в рамках которого статическое поле и излучениие принято ( было ? ) различать.
Вот кстати уже не совсем свежий пример:
Цитата: hedin от 15.02.2011 23:40:00
Готов согласиться, что на самом деле нет никаких физических способов различить статическое электрическое поле от постоянно пробегающих волн. Грубая аналогия - тащат щепку к берегу с постоянной силой за невидимую леску, или эту щепку прибивает к берегу равномерной мелкой волной, по движению самой щепки ( нашего пробного тела ) не различить.
Но как я уже показал, физики пока статику и излучение ( волну ) как-то различают. Конечно при этом забавно наблюдать как они же и выводят волновое уравнение из статики.
- +0.00 / 0
-
|
|
Yuri Rus ( Слушатель ) |
| 13 апр 2011 в 04:14 |
- ...
Цитата: Поверонов от 13.04.2011 00:07:31
Ув. Поверонов, во-первых, в цитированном тексте Leigh Page речь идет НЕ о статическом электрическом поле, а об электромагнитных волнах. Я не показывал, как там было выведено волновое уравнение (156-2) для Е. Вот так:


Обратите внимание на фразу (в переводе на русский):
Это уравнения волны, распространяющейся с фазовой скоростью

Именно благодаря тому, что Максвелл получил волновые уравнения для E и B и предсказал существование электромагнитных волн, его теория и была признана научным сообществом. Можно сказать, это самое главное в теории Максвелла.
Во-вторых, о какой статике может идти речь, если заряд движется? Если Вы посмотрите книгу Фейнман Р., Лейтон Р., Сэндс М. «Фейнмановские Лекции по Физике», т. 6 «Электродинамика», гл. 21, § 2, то увидите, что потенциалы φ и А определяются волновыми уравнениями
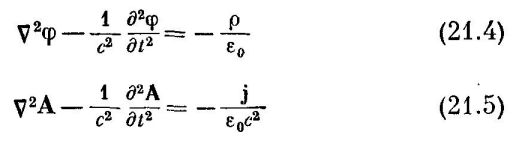
Далее в той же главе 21, в § 6 "Потенциалы заряда, движущегося с ростоянной скоростью; формула Лоренца", преобразования Лоренца выводятся именно из запаздывания потенциалов, распространяющихся как волны со скоростью с:



Пардон за такие длинные цитаты. Я хотел подчеркнуть, что волны, распространяющиеся со скоростью света с от движущегося заряда, играют фундаментальную, ключевую роль в электродинамике - как в теории Максвелла, так и в теории относительности.
Это совершенно не значит, что я согласен с любой из этих теорий. Я просто отвечаю на Ваш вопрос о различении между статикой и излучением в физике, и пытаюсь показать, что в данном случае - электродинамика однозначно выбирает излучение.
- +0.00 / 0
-
|
|
Поверонов ( Слушатель ) |
| 14 апр 2011 в 01:43 |
- ...
Цитата: Yuri Rus от 13.04.2011 04:14:45
Собственно подозрение о статичности поля в рассматриваемом отрывке возникло из следующего абзаца
Цитата: Yuri Rus от 12.04.2011 10:31:01
в котором фактически и постулируется статичность поля, которое заряд как бы "тащит за собой". Но если Вы уверены, что в отрывке и у них речь идет об излучении, то тем более нет проблем. Ждем продолжения.
- +0.00 / 0
-
|
|
Yuri Rus ( Слушатель ) |
| 14 апр 2011 в 02:48 |
- ...
Цитата: Поверонов от 14.04.2011 01:43:30
Понимаете, Ваш вопрос о статичности поля хороший и правильный, он безусловно имеет смысл. Но он очень преждевременный - мне пришлось бы залезть слишком далеко вперед. Поэтому я сейчас уклоняюсь от ответа на него и ссылаюсь на то, что в разбираемом вопросе в рамках теории Максвелла и ТО речь идет о бегущих волнах.
Позже к нему безусловно имеет смысл вернуться - когда мы будем говорить о том, что же такое Кулоновское поле, какой его физический смысл (излучение ли волн, смещение ли частиц светопроводящей среды, и т.д.). Я буду стараться показать, что существует только одно физическое поле, а все известные физике силы являются его проявлениями при движении заряженных частиц. Закон Кулона, как я утверждаю, неверен, он приблизителен - на самом деле, это поле имеет знакопеременный характер. Знакопеременность означает, что никакого сильного и слабого взаимодействий вообще нет, это ошибочная интерпретация экспериментальных данных. Но до этого еще дойти надо.
- +0.00 / 0
-