Тред №324428
208
Дискуссия
новая
|
|
Yuri Rus ( Слушатель ) |
| 24 мая 2011 в 07:20 |
Примечание: я пользуюсь Firefox и он показывает все формулы нормально. Но сейчас я глянул на формулы в Google Chrome и Internet Explorer и обнаружил, что по крайней мере одну букву они оба не показывают (нижний индекс маленькую а):
pₐ = pa
Если есть возможность, лучше смотреть в Firefox.
-------------------------
Сейчас я собираюсь обсудить вопрос о выводе преобразований Лоренца. Однако, если я сразу начну говорить о движении электрического заряда и волновом уравнении для электростатического потенциала φ, во-первых, возникнет впечатление, что это относится только к волнам, распространяющимся со скоростью света. Во-вторых, это будет не очень очевидно, потому что «пощупать пальцами» явления, происходящие со скоростью света, нельзя. Как следить за динамикой распространения таких волн, за промежуточными этапами? Даже измерить скорость света в одном направлении – и то нельзя; можно только туда и обратно. Кроме того, все слишком привыкли к идее, что скорость света играет особенную роль, там всё по-другому. Поэтому я решил начать со звуковых волн, как более наглядных, понятных, которые сравнительно медленные и процесс распространения которых можно наблюдать в динамике. А потом уже мы применим полученные результаты к движущимся зарядам и сравним с тем, что говорит общепринятая физическая теория.
Формул будет довольно много, но они очень простые. Единственная трудность – форма записи, в одну линию, со множеством скобок. Я не хочу переводить каждую формулу в jpg формат, это займет слишком много времени. А иного способа дать формулы на форуме в привычном виде я не знаю. Хорошо хоть, нашел возможность делать subscript и superscript индексы маленькими цифрами и некоторыми буквами (а то было бы, допустим, ∂2u/∂t2, а не ∂²u/∂t²).
Начну я с «нулевого приближения» – это означает, что последовательные волны от движущегося источника не взаимодействуют; каждая единичная волна распространяется радиально с фазовой скоростью с в покоящейся среде. Рассмотрим движущийся источник звуковых волн (продольных) в жидкости. Здесь есть такая проблема. Я уже говорил, что решение Дюамеля неоднородного волнового уравнения неверно. Кроме того, само волновое уравнение в случае наличия источника должно записываться совсем не так:
∂²u/∂t² – c²∇²u = S(x, y, z, t)
В нем должны присутствовать координаты источника (ξ, η, ζ) и время излучения единичной волны ԏ. Я пока не хочу вводить это более сложное уравнение. Я хочу показать, что к выводам об ошибочности волнового уравнения (и как следствие – почти всей физики) можно прийти даже в рамках существующего математического аппарата физики. Мне кажется, большинству читателей будет легче понять, в чем заключаются эти ошибки, если изложение не будет привязано к новому мат. аппарату, если мы будем пользоваться привычным математическим языком «старой» физики. Потом уже можно говорить и о новом мат. аппарате.
Достичь этой цели можно, если, вместо неоднородного, мы будем пользоваться однородным волновым уравнением
∂²p/∂t² – c²∇²p = 0,
где p – звуковое давление (разность между полным давлением и равновесным давлением в жидкости).
Это однородное уравнение действительно решено правильно (Д'Аламбером и Пуассоном), никаких претензий я не имею. И для него мы действительно можем обойтись лишь тремя пространственными координатами и одной временной – (x, y, z, t).
Пусть в момент времени t=0 среда покоится, причем p и dp/dt равны нулю везде, кроме точки (0, 0, 0), где находится источник. Источник не точечный, он представляет собой сферу радиуса a. Обозначим давление на поверхности этой сферы как pₐ(t). В нулевой момент времени оно равно pₐ(0) – некое давление, которое мы выбрали. Мы можем найти решение этого однородного уравнения, пользуясь формулой Пуассона (см. цитаты из книги Кошлякова и др. на второй странице ветки). Это – единичная сферическая волна, распространяющаяся со скоростью с, центром которой является точка (0, 0, 0). Мы также можем описать распространение этой волны при помощи более простого уравнения:
r₁(t) = ct = i x(t) + j y(t) + k z(t)
где с – вектор скорости звука; r₁(t) – радиус-вектор первой единичной волны: x(t), y(t), z(t) – координаты какой-то точки на этом фронте в момент времени t.
r₁(t) = (x²(t) + y²(t) + z²(t))½
В СО покоящейся среды, последовательные стадии распространения одной единичной волны в разные моменты времени выглядит следующим образом:
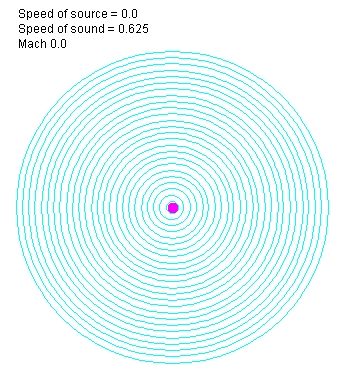
Здесь и везде, когда я использую термин «единичная волна», имеется в виду маленький кусочек волны, излученной за промежуток времени dt. Этот термин имеет совсем другой смысл, чем волна длительностью λ с периодом 2π. Пардон, если это внесло путаницу в мои предыдущие сообщения.
За время dt источник сместился в точку (v dt, 0, 0), и давление на его поверхности стало pₐ(dt). Мы можем найти решение этого уравнения, опять пользуясь формулой Пуассона, причем опять полагая, что вся остальная среда покоится. Распространение второй единичной волны подчиняется закону:
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Затем мы можем найти решение для распространения единичной сферической волны, излученной в момент времени 2dt, из следующей точки – (2v dt, 0, 0).
r₃(t) – i 2v dt = c(t – 2dt)
(x(t) – 2v dt)² + y²(t) + z²(t) = c² (t – 2dt)²
И так далее. В СО покоящейся среды, мгновенный снимок последовательных единичных волн выглядит так:
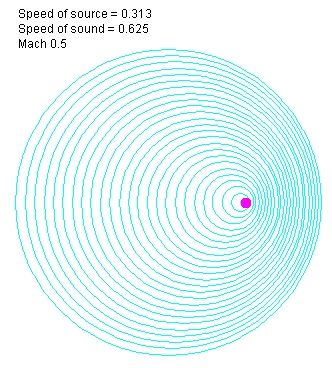
В СО движущегося источника, эта же картинка описывает как распространение единичной волны в разные моменты времени, так и мгновенный снимок последовательных фронтов волн.
Этот подход с единичными волнами, каждая из которых описывается однородным волновым уравнением, очень похож на описание проблемы излучения из книги Куранта «Методы математической физики», т. 2, стр. 191 (уже цитированной на второй странице ветки):

Пара слов о терминах. Сила, действующая на элемент объема ΔV, пропорциональна градиенту давления:
ΔF = – ∇p ΔxΔyΔz
Это уравнение очень похоже на уравнение для силы гравитации F как градиента гравитационного потенциала φ
F = – m ∇φ
и уравнение для силы электростатического взаимодействия двух зарядов как градиента электростатического потенциала φ
F = – q ∇φ = q E
E = – ∇φ
Для гравитации, φ m, и для электростатики, φ q, имеют размерность энергии и представляют собой потенциальную энергию. Аналогично, p ΔV имеет размерность энергии и представляет собой часть потенциальной энергии жидкости или газа (напомню, что энтальпия H = U + pV, внутренняя энергия плюс давление, умноженное на объем). Давление, таким образом, это удельная потенциальная энергия (часть оной): потенциальная энергия, разделенная на единицу объема. Зачем я это подчеркиваю? Затем, что есть такое часто используемое понятие как «эквипотенциальные поверхности», и все привыкли, что сила перпендикулярна этим поверхностям. Тогда как понятие «поверхности равного давления» используется намного реже и, мне кажется, если я стану его применять, читателям будет не настолько очевидно, что сила давления должна быть перпендикулярна этим поверхностям. Так что я буду в дальнейшем, говоря об эквипотенциальных поверхностях, иметь в виду поверхности равного давления. В данном случае, они имеют один и тот же смысл.
Далее, напомню определение: «ФРОНТ ВОЛНЫ - поверхность, окружающая источник колебаний, все точки которой имеют одинаковые фазы колебаний. Фронт волны может быть сферой (сферическая волна) или иметь более сложную форму». Понятие единичной волны, которым я здесь пользуюсь, в принципе, совпадает с понятием фронта волны.
В статическом случае, когда источник звуковых волн неподвижен, каждый фронт волны совпадает с сферической эквипотенциальной поверхностью – давление во всех точках любого фронта одинаково. Сила направлена по нормали к поверхности фронта волны – радиально (сила, по определению, направлена по нормали к эквипотенциальной поверхности).
Сделаем предположение, что при движении источника фронт каждой волны тоже совпадает с эквипотенциальной поверхностью, то есть давление во всех его точках одинаково и сила направлена по нормали к поверхности фронта волны. Возможно, это предположение выполняется не всегда или вообще не выполняется, тогда в будущем мы его скорректируем. Сейчас же построим модель распространения звуковых волн, исходя из этого предположения.
Это означает, что в любой момент времени давление в каждой точке какой-либо единичной волны одинаково – если одинаково давление на всей поверхности источника pₐ(t). А это давление определяется внешней силой, которую мы задаем сами. Примем, что внешняя сила одинакова на поверхности источника – значит, будет одинаковой.
Тогда при распространении первой единичной волны, излученной в момент времени 0 из точки (0, 0, 0), давление в каждой ее точке будет меняться по закону:
p₁(x, y, z, t) = pₐ(0) a / r₁(t) = pₐ(0) a / (ct)
Давление в каждой точке второй единичной волны будет меняться по закону:
p₂(x, y, z, t) = pₐ(dt) a / |r₂(t) – v dt| = pₐ(dt) a / (c (t – dt))
Третьей:
p₃(x, y, z, t) = pₐ(2dt) a / |r₃(t) – 2v dt| = pₐ(2dt) a / (c (t – 2dt))
Как я буду писать ниже, в электродинамике для потенциалов движущихся зарядов используется формула Лиенара-Вихерта, с дополнительным множителем 1 / (1 – r’∙v / (r’c)), таким же, как в уравнении Доплера. Но мы этот множитель сейчас вводить не будем. Он играет фундаментальную роль в рождении теории относительности и я буду очень долго о нем говорить немного позже. Пока же обойдемся без него.
Давайте еще более упростим нашу модель. Пусть длина волны λ (уже не единичной волны, а волны с периодом 2π) много больше, чем радиус a источника. Тогда, если нас интересуют волны вблизи от источника, мы можем считать, что за то время, когда волны проходят расстояние порядка нескольких десятков радиусов источника, величина pₐ практически не меняется: pₐ ≈ const. Пусть, далее, pₐ > 0, то есть сила, действующая на частицы среды, направлена от источника.
Еще раз посмотрим на эту картинку:
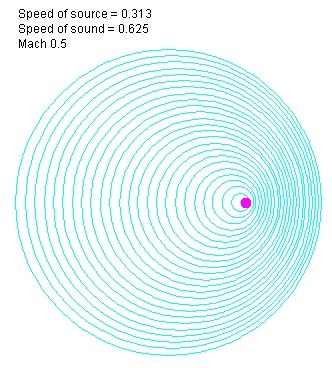
Согласно нашему предположению о совпадении фронтов волн с эквипотенциальными поверхностями, эти сферы – поверхности равного давления. Сила, как градиент давления, направлена по нормали к поверхности этих сфер. Проведем непрерывные силовые линии от источника таким образом, чтобы они были перпендикулярны всем этим сферам. Легко видеть, что силовые линии должны быть кривыми, причем загнутыми вперед, по направлению движения источника:
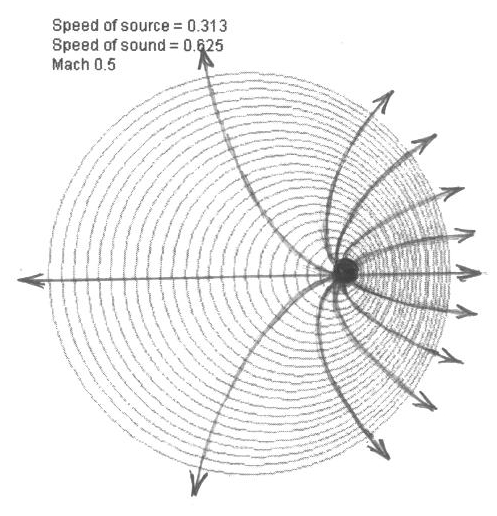
Если вы смотрите на эти силовые линии из СО покоящейся среды, в этом нет ничего удивительного, ведь это относится к последовательным единичным волнам, излученным из разных точек. Но напомню, что в СО источника так выглядят не только силовые линии, перпендикулярные фронтам последовательных единичных волн, но и силовые линии, перпендикулярные фронту одной и той же единичной волны в разные моменты времени. Обратите внимание, как сгущаются силовые линии перед источником: через единицу поверхности перед источником проходит намного больше силовых линий, чем сзади от него. Никакой симметрии «перед-зад» здесь и в помине нет.
pₐ = pa
Если есть возможность, лучше смотреть в Firefox.
-------------------------
Сейчас я собираюсь обсудить вопрос о выводе преобразований Лоренца. Однако, если я сразу начну говорить о движении электрического заряда и волновом уравнении для электростатического потенциала φ, во-первых, возникнет впечатление, что это относится только к волнам, распространяющимся со скоростью света. Во-вторых, это будет не очень очевидно, потому что «пощупать пальцами» явления, происходящие со скоростью света, нельзя. Как следить за динамикой распространения таких волн, за промежуточными этапами? Даже измерить скорость света в одном направлении – и то нельзя; можно только туда и обратно. Кроме того, все слишком привыкли к идее, что скорость света играет особенную роль, там всё по-другому. Поэтому я решил начать со звуковых волн, как более наглядных, понятных, которые сравнительно медленные и процесс распространения которых можно наблюдать в динамике. А потом уже мы применим полученные результаты к движущимся зарядам и сравним с тем, что говорит общепринятая физическая теория.
Формул будет довольно много, но они очень простые. Единственная трудность – форма записи, в одну линию, со множеством скобок. Я не хочу переводить каждую формулу в jpg формат, это займет слишком много времени. А иного способа дать формулы на форуме в привычном виде я не знаю. Хорошо хоть, нашел возможность делать subscript и superscript индексы маленькими цифрами и некоторыми буквами (а то было бы, допустим, ∂2u/∂t2, а не ∂²u/∂t²).
Начну я с «нулевого приближения» – это означает, что последовательные волны от движущегося источника не взаимодействуют; каждая единичная волна распространяется радиально с фазовой скоростью с в покоящейся среде. Рассмотрим движущийся источник звуковых волн (продольных) в жидкости. Здесь есть такая проблема. Я уже говорил, что решение Дюамеля неоднородного волнового уравнения неверно. Кроме того, само волновое уравнение в случае наличия источника должно записываться совсем не так:
∂²u/∂t² – c²∇²u = S(x, y, z, t)
В нем должны присутствовать координаты источника (ξ, η, ζ) и время излучения единичной волны ԏ. Я пока не хочу вводить это более сложное уравнение. Я хочу показать, что к выводам об ошибочности волнового уравнения (и как следствие – почти всей физики) можно прийти даже в рамках существующего математического аппарата физики. Мне кажется, большинству читателей будет легче понять, в чем заключаются эти ошибки, если изложение не будет привязано к новому мат. аппарату, если мы будем пользоваться привычным математическим языком «старой» физики. Потом уже можно говорить и о новом мат. аппарате.
Достичь этой цели можно, если, вместо неоднородного, мы будем пользоваться однородным волновым уравнением
∂²p/∂t² – c²∇²p = 0,
где p – звуковое давление (разность между полным давлением и равновесным давлением в жидкости).
Это однородное уравнение действительно решено правильно (Д'Аламбером и Пуассоном), никаких претензий я не имею. И для него мы действительно можем обойтись лишь тремя пространственными координатами и одной временной – (x, y, z, t).
Пусть в момент времени t=0 среда покоится, причем p и dp/dt равны нулю везде, кроме точки (0, 0, 0), где находится источник. Источник не точечный, он представляет собой сферу радиуса a. Обозначим давление на поверхности этой сферы как pₐ(t). В нулевой момент времени оно равно pₐ(0) – некое давление, которое мы выбрали. Мы можем найти решение этого однородного уравнения, пользуясь формулой Пуассона (см. цитаты из книги Кошлякова и др. на второй странице ветки). Это – единичная сферическая волна, распространяющаяся со скоростью с, центром которой является точка (0, 0, 0). Мы также можем описать распространение этой волны при помощи более простого уравнения:
r₁(t) = ct = i x(t) + j y(t) + k z(t)
где с – вектор скорости звука; r₁(t) – радиус-вектор первой единичной волны: x(t), y(t), z(t) – координаты какой-то точки на этом фронте в момент времени t.
r₁(t) = (x²(t) + y²(t) + z²(t))½
В СО покоящейся среды, последовательные стадии распространения одной единичной волны в разные моменты времени выглядит следующим образом:

Здесь и везде, когда я использую термин «единичная волна», имеется в виду маленький кусочек волны, излученной за промежуток времени dt. Этот термин имеет совсем другой смысл, чем волна длительностью λ с периодом 2π. Пардон, если это внесло путаницу в мои предыдущие сообщения.
За время dt источник сместился в точку (v dt, 0, 0), и давление на его поверхности стало pₐ(dt). Мы можем найти решение этого уравнения, опять пользуясь формулой Пуассона, причем опять полагая, что вся остальная среда покоится. Распространение второй единичной волны подчиняется закону:
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Затем мы можем найти решение для распространения единичной сферической волны, излученной в момент времени 2dt, из следующей точки – (2v dt, 0, 0).
r₃(t) – i 2v dt = c(t – 2dt)
(x(t) – 2v dt)² + y²(t) + z²(t) = c² (t – 2dt)²
И так далее. В СО покоящейся среды, мгновенный снимок последовательных единичных волн выглядит так:

В СО движущегося источника, эта же картинка описывает как распространение единичной волны в разные моменты времени, так и мгновенный снимок последовательных фронтов волн.
Этот подход с единичными волнами, каждая из которых описывается однородным волновым уравнением, очень похож на описание проблемы излучения из книги Куранта «Методы математической физики», т. 2, стр. 191 (уже цитированной на второй странице ветки):

Пара слов о терминах. Сила, действующая на элемент объема ΔV, пропорциональна градиенту давления:
ΔF = – ∇p ΔxΔyΔz
Это уравнение очень похоже на уравнение для силы гравитации F как градиента гравитационного потенциала φ
F = – m ∇φ
и уравнение для силы электростатического взаимодействия двух зарядов как градиента электростатического потенциала φ
F = – q ∇φ = q E
E = – ∇φ
Для гравитации, φ m, и для электростатики, φ q, имеют размерность энергии и представляют собой потенциальную энергию. Аналогично, p ΔV имеет размерность энергии и представляет собой часть потенциальной энергии жидкости или газа (напомню, что энтальпия H = U + pV, внутренняя энергия плюс давление, умноженное на объем). Давление, таким образом, это удельная потенциальная энергия (часть оной): потенциальная энергия, разделенная на единицу объема. Зачем я это подчеркиваю? Затем, что есть такое часто используемое понятие как «эквипотенциальные поверхности», и все привыкли, что сила перпендикулярна этим поверхностям. Тогда как понятие «поверхности равного давления» используется намного реже и, мне кажется, если я стану его применять, читателям будет не настолько очевидно, что сила давления должна быть перпендикулярна этим поверхностям. Так что я буду в дальнейшем, говоря об эквипотенциальных поверхностях, иметь в виду поверхности равного давления. В данном случае, они имеют один и тот же смысл.
Далее, напомню определение: «ФРОНТ ВОЛНЫ - поверхность, окружающая источник колебаний, все точки которой имеют одинаковые фазы колебаний. Фронт волны может быть сферой (сферическая волна) или иметь более сложную форму». Понятие единичной волны, которым я здесь пользуюсь, в принципе, совпадает с понятием фронта волны.
В статическом случае, когда источник звуковых волн неподвижен, каждый фронт волны совпадает с сферической эквипотенциальной поверхностью – давление во всех точках любого фронта одинаково. Сила направлена по нормали к поверхности фронта волны – радиально (сила, по определению, направлена по нормали к эквипотенциальной поверхности).
Сделаем предположение, что при движении источника фронт каждой волны тоже совпадает с эквипотенциальной поверхностью, то есть давление во всех его точках одинаково и сила направлена по нормали к поверхности фронта волны. Возможно, это предположение выполняется не всегда или вообще не выполняется, тогда в будущем мы его скорректируем. Сейчас же построим модель распространения звуковых волн, исходя из этого предположения.
Это означает, что в любой момент времени давление в каждой точке какой-либо единичной волны одинаково – если одинаково давление на всей поверхности источника pₐ(t). А это давление определяется внешней силой, которую мы задаем сами. Примем, что внешняя сила одинакова на поверхности источника – значит, будет одинаковой.
Тогда при распространении первой единичной волны, излученной в момент времени 0 из точки (0, 0, 0), давление в каждой ее точке будет меняться по закону:
p₁(x, y, z, t) = pₐ(0) a / r₁(t) = pₐ(0) a / (ct)
Давление в каждой точке второй единичной волны будет меняться по закону:
p₂(x, y, z, t) = pₐ(dt) a / |r₂(t) – v dt| = pₐ(dt) a / (c (t – dt))
Третьей:
p₃(x, y, z, t) = pₐ(2dt) a / |r₃(t) – 2v dt| = pₐ(2dt) a / (c (t – 2dt))
Как я буду писать ниже, в электродинамике для потенциалов движущихся зарядов используется формула Лиенара-Вихерта, с дополнительным множителем 1 / (1 – r’∙v / (r’c)), таким же, как в уравнении Доплера. Но мы этот множитель сейчас вводить не будем. Он играет фундаментальную роль в рождении теории относительности и я буду очень долго о нем говорить немного позже. Пока же обойдемся без него.
Давайте еще более упростим нашу модель. Пусть длина волны λ (уже не единичной волны, а волны с периодом 2π) много больше, чем радиус a источника. Тогда, если нас интересуют волны вблизи от источника, мы можем считать, что за то время, когда волны проходят расстояние порядка нескольких десятков радиусов источника, величина pₐ практически не меняется: pₐ ≈ const. Пусть, далее, pₐ > 0, то есть сила, действующая на частицы среды, направлена от источника.
Еще раз посмотрим на эту картинку:

Согласно нашему предположению о совпадении фронтов волн с эквипотенциальными поверхностями, эти сферы – поверхности равного давления. Сила, как градиент давления, направлена по нормали к поверхности этих сфер. Проведем непрерывные силовые линии от источника таким образом, чтобы они были перпендикулярны всем этим сферам. Легко видеть, что силовые линии должны быть кривыми, причем загнутыми вперед, по направлению движения источника:

Если вы смотрите на эти силовые линии из СО покоящейся среды, в этом нет ничего удивительного, ведь это относится к последовательным единичным волнам, излученным из разных точек. Но напомню, что в СО источника так выглядят не только силовые линии, перпендикулярные фронтам последовательных единичных волн, но и силовые линии, перпендикулярные фронту одной и той же единичной волны в разные моменты времени. Обратите внимание, как сгущаются силовые линии перед источником: через единицу поверхности перед источником проходит намного больше силовых линий, чем сзади от него. Никакой симметрии «перед-зад» здесь и в помине нет.
Отредактировано: Yuri Rus - 02 дек 2019 в 03:31
- +0.00 / 0
-
ОТВЕТЫ (2)
|
|
Поверонов ( Слушатель ) |
| 28 мая 2011 в 12:00 |
Цитата: Yuri Rus от 24.05.2011 07:20:19
Может я конечно не заметил, тогда просто ткните носом в текст.
При рассмотрении взаимодействия волн от движущегося источника в передней полусфере по направлению движения источника ( точнее - в определенном конусе ) ВСЕГДА должно иметь место наложение новой и запаздывающих волн, так как всегда существует геометрическое место точек, где новая волна догоняет старую.По существу в этом конусе уже не будет "чистых" волн, а только динамический след их многократной интерференции. Интерференция запаздывающих волн - это просто принцип сложения векторов сил, которым пренебрегать нельзя, так как иначе это не силы, а значит - не поле, а значит - не волны ( то же и для давления ибо давление - тоже сила лишь "размазанная по площади" ).
А если период волн так велик, что последовательные волны никогда не пересекаются, то и об их взаимодействии не может идти речь:
Цитата: Yuri Rus от 24.05.2011 07:20:19
- +0.00 / 0
-
|
|
Yuri Rus ( Слушатель ) |
| 28 мая 2011 в 12:26 |
Цитата: Поверонов от 28.05.2011 12:00:47
Я до этого пока не дошел, собираюсь говорить в дальнейшем. Вообще говоря, даже если период очень большой, последовательные волны все равно взаимодействуют и там происходит не только интерференция, но и другие важные явления. Но я пользуюсь другой терминологией и, вероятно, другими литературными источниками, чем то, что Вы написали. Не могли бы Вы уточнить, дать какие-то ссылки, чтобы я точнее понял, что Вы имеете в виду?
- +0.00 / 0
-