Тред №324434

Давайте, наконец, рассмотрим вывод самого уравнения Лиенара-Вихерта. Где же там могут быть ошибки?

Будем опять следовать Фейнману. Я перескажу его доказательство своими словами, чтобы сделать его более ясным и усилить некоторые моменты. Дело в том, что некоторые ключевые вещи он прямо не говорит, о них можно только догадаться по его рисункам и формулам. Если я неправильно понял Фейнмана, прошу меня поправить. Уравнение Лиенара-Вихерта играет ключевую роль для вывода преобразований Лоренца и для теории относительности, поэтому этот вопрос заслуживает того, чтобы на него потратить какое-то время, чтобы добиться полной ясности.

Итак, Фейнман сначала оговаривает, что точечный заряд – это очень маленький заряженный шарик с плотностью заряда  ρ(x, y, z).  Потом пишет:
 

 
И ниже:
 

 
Сейчас я перехожу к своей интерпретации аргументации Фейнмана, поскольку у него это не сформулировано достаточно явно и четко.

Потенциал  φ  в точке (1) в момент времени  t  является суммой единичных волн потенциала, каждая из которых была излучена в разные моменты времени и на разных расстояниях от точки (1). Причем за то время, пока сигнал от самого дальнего элемента заряда дойдет до самого ближнего элемента, этот ближний элемент успеет пройти какое-то расстояние. Вместо  стороны куба  a,  эффективная длина заряда становится  a/(1 – v/c),  причем считается, что плотность заряда  ρ  не меняется. Судя по рисунку 21.7, логика здесь такая: объем (не заряд, а именно объем пространства!) размерами  a ⨯ a ⨯ a/(1 – v/c),  через который проходит заряд за время путешествия сигнала от самого дальнего до самого ближнего участка заряда, разбивается на некоторое число элементов толщиной  w.  Затем сигналы от этих элементов объема суммируются следующим образом: сначала к сумме добавляется сигнал (единичная волна потенциала) от самого дальнего элемента объема, где в этот момент находится первый элемент заряда с толщиной  w  и плотностью заряда  ρ.  Потом мы переходим к следующему элементу объема толщиной  w  и добавляем к сумме его сигнал, излученный в следующий момент времени (чтобы сигналы от всех элементов объема достигли точки (1) одновременно). При этом, первый элемент заряда, который был раньше в первом элементе объема, успел частично сместиться во второй элемент объема. Допустим, скорость заряда  v = 0.9 c  и мы измеряем потенциал спереди от движущегося заряда. Это означает, что 90% второго элемента объема будут заполнены первым элементом заряда – и он опять вносит вклад в сигнал, который добавляется к общей сумме. Оставшиеся 10% объема второго элемента объема заполнены вторым элементом заряда, так что плотность заряда остается той же самой – ρ.  В следующий момент времени, все тот же первый элемент заряда займет 80% третьего элемента объема – и внесет 80% вклада в сигнал от него, второй элемент заряда внесет 20% вклада. Плотность заряда та же. И т.д.

Поскольку мне пару раз напоминали, что ГА – это политико-экономический форум и не место для дискуссий физики, предложу политико-экономическую аналогию этому процессу. На злобу дня: представьте себе, что М. Каддафи прогнал всех аль-каидовцев из Ливии и они собрались на острове Лампедуза. И требуют еды и воды, мы же, мол, для вас демократию и гуманитарные бомбардировки, то есть ценности, защищали. И привезли добросердечные итальянцы им еды и воды на 10 дней на 10 грузовиках, и сказали: «Становитесь в очереди к грузовикам. Каждый получит рацион на один день только. Завтра получите рацион еще на один день». А хитрые аль-каидовцы, зная, что итальянцы их друг от друга отличить не смогут, каждый заняли 10 очередей ко всем 10 грузовикам. И в итоге итальянцы обнаружили, что все грузовики оказались пустыми всего за один день. И каждый день они привозят по 10 грузовиков, и всегда те загадочным образом опустошаются, хотя они очень следят, чтобы на руки выдавать только по одному рациону. А раскормленные аль-каидовцы требуют еще и еще.

Думаю, требование политико-экономичности я выполнил? Можно вернуться к физике?

Для  v = 0.9 c,  поправочный (ЛВД) множитель равен  1 / (1 – 0.9) = 10.  Это означает, что каждый элемент заряда внесет свой вклад в сигнал не один раз, а 10 раз, потому что суммирование производится не по элементам заряда, а по элементам объема, так что каждый элемент заряда успевает «отметиться» в разных элементах объема (вклад всех, кроме первого и последнего элементов заряда, сначала растет от 10% до 100%, потом опять убывает до 10%). В этом и заключается смысл уравнения Лиенара-Вихерта.

Мда. Свистнуто, не спорю, действительно свистнуто, но, если говорить беспристрастно, свистнуто очень средне! Отметьте, это уравнение – один из краеугольных камней современной физики, на нем стоит теория относительности. А само это уравнение стоит на идее, что суммировать сигнал от элементов заряда надо не по самим элементам заряда, а по тому объему пространства, через который они прошли за время путешествия сигнала от дальнего конца заряда к ближнему, причем суммирование производится таким образом, что каждый элемент заряда учитывается не один, а много раз.

Не слишком ли это шаткое основание для современной физики?

Я думаю, что намного больше физического смысла имеет иная процедура суммирования – по самим элементам заряда. При этой процедуре, каждый элемент заряда вносит вклад в общий потенциал только один раз. Допустим, для  v = 0.9 c,  суммирование будет выглядеть следующим образом:

◘■■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□■◘■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□■■◘■■□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■◘■□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■■◘

В первый момент времени, сигнал излучается самым дальним элементом заряда. Во второй момент времени, сигнал излучается вторым элементом заряда, который за это время успел сместиться на расстояние  9w.  В третий момент времени, сигнал излучается третьим элементом заряда, который за это время успел сместиться еще на расстояние  9w.  И так далее. В итоге, каждый элемент заряда внесет свой вклад в суммарный потенциал только один раз и уравнение для потенциала будет, все-таки,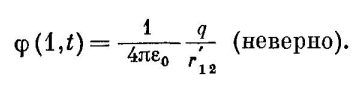
 

 
На первой странице ветки, я написал:

Я буду в основном говорить о волнах и волновом уравнении. Отмечу, что уравнения динамики жидкости и твердого тела в классической механике обычно выражаются в двух формах – лагранжевой и эйлеровой. Уравнения в форме Лагранжа описывают движения индивидуальной частицы жидкости или твердого тела (точнее, некоторого элемента объема, состоящего из многих частиц). Координаты  (x, y, z)  частицы считаются функциями времени и трех параметров  (a, b, c),  в качестве которых часто выбираются координаты частицы при  t = 0. Уравнения в форме Эйлера описывают  то, что происходит в некоторой точке пространства  (x, y, z)  (точнее, с неким бесконечно малым элементом длины, поверхности или объема) на протяжении некоторого промежутка времени. Рассматриваются силы, скорости, смещения и т.д. применительно именно к этому малому элементу, и для него выводятся дифференциальные уравнения. Для полного описания поведения системы, задаются еще начальные и граничные условия.

Я предлагаю третий подход. Вместо того, чтобы рассматривать силы, скорости и смещения некого элемента среды (или некой частицы), расположенного в произвольной точке пространства, мы будем начинать анализ распространения волн с их источника. Есть источник, он создает какую-то силу, действующую на окружающие его элементы среды (которые не расположены где-то далеко, а прямо и непосредственно контактируют с источником), эта сила вызывает смещение этих элементов, которые приобретают ускорение, скорость, далее они воздействуют на соседние с ними элементы среды, и т.д. Причем, что важно с физической точки зрения – источник создает не единичную волну, которая затем распространяется по покоящейся  среде, а множество волн, непрерывно генерирует их. Кроме того, если мы хотим обсудить теорию относительности, мы должны рассмотреть движение источника относительно среды.

Суммирование по элементам заряда, то есть по элементам источника, и есть пример этого третьего подхода.

Это очень важный момент. Уравнение Лиенара-Вихерта является типичным уравнением в форме Эйлера – и решено в полном соответствии с правилами решений этих уравнений мат. физики. Мне не попадалась его запись в форме Лагранжа, но, надо думать, и в том виде его решение было бы точно таким же, поскольку, вроде бы, принципиальных расхождений между подходами Лагранжа и Эйлера до сих пор не наблюдалось. Та ошибка, на которую я указываю, в рамках мат. физики ошибкой вовсе не считается. Мат. физика полна подобных уравнений – таковы очень многие уравнения динамики материальных сред, в частности, гидродинамики и электродинамики. Я имею в виду те уравнения, где один и тот же элемент массы или заряда, благодаря своему движению относительно элемента пространства, учитывается не один раз, а  k  раз, где  k  может быть и больше, и меньше единицы.

Это только одна из серьезных ошибок мат. физики, которые, как я считаю, и привели к тому, что почти вся физика (и классическая тоже) как наука к настоящему времени неверна.

Я опирался на подход Фейнмана к выводу уравнения Лиенара-Вихерта, но в учебниках встречаются и другие подходы. Допустим, в книге Беккер Р. «Теория Электричества. Том 2. Электронная теория» (1941), на стр. 61-65 приводится другой вариант этого вывода. В книге Джексон Дж. «Классическая электродинамика» (1965), на стр. 509-510 приводится вывод этого уравнения при помощи функций Грина и  δ-функции Дирака. Я приведу цитаты в конце этого сообщения.

Смысл всех этих подходов, при внешних различиях, один и тот же. Все они исходят из того, что вклад элементов заряда надо учитывать много раз, по мере их прохождения через разные элементы объема. Изложение Фейнмана мне просто нравится больше – из-за большей наглядности и «физичности». В отличие от многих физиков, он стремился найти и объяснить именно физический смысл уравнений физики, не считал, что уравнения и есть вся физика.

Итак, подытожим. Уравнение Лиенара-Вихерта неверно – запаздывание не приводит к появлению дополнительного множителя у потенциала, распространяющегося от источника. Тем не менее, дополнительный (по сравнению с покоящимся источником) множитель может появиться – из-за изменения формы заряда при движении или перераспределения плотности заряда; для источника звука – из-за изменения плотности среды вокруг источника. Именно это изменение плотности заряда или среды вокруг источника и передается во все стороны – в «нулевом приближении», без искажений. Запаздывание же к этому никакого отношения не имеет.

Беккер Р. «Теория Электричества. Том 2. Электронная теория» (1941), стр. 61-65:
 

 

 

 

 

 
Джексон Дж. «Классическая электродинамика» (1965), стр. 509-510: