Тред №325724

Но вывод уравнения Лиенара-Вихерта, тем не менее, неверен. Никакого множителя вида  1 / (1 – r’∙v / (r’ c))  при движении зарядов или источников звука не появляется. В сообщении, где я анализировал вывод уравнения Лиенара-Вихерта, это было сделано именно что качественно, на пальцах. Упрощать далее довольно трудно. Разве что могу выделить наиболее важный кусочек и изложить его слегка иначе.

Итак, задача формулируется следующим образом. Мы хотим знать, чему равен потенциал от движущегося заряда в момент времени  t  в покоящейся точке  P.  Это делается при помощи интеграла по объему от плотности заряда и расстояния до заряда в момент излучения сигнала: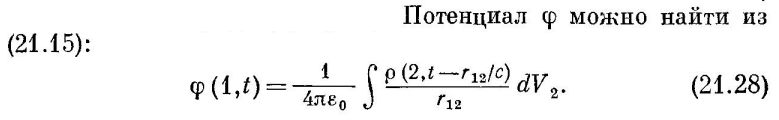
 

 
Поскольку заряд движется, то для того, чтобы достичь точки Р одновременно, сигналы от разных частей заряда должны быть излучены в разные моменты времени. Чем дальше от точки Р находится какой-то элемент заряда, тем раньше должен быть излучен сигнал от него. Причем за то время, пока сигнал от самого дальнего элемента заряда дойдет до самого ближнего элемента, этот ближний элемент успеет пройти какое-то расстояние.

Уравнения динамики записываются обычно в 2 формах - лагранжевой и эйлеровой. Уравнения в форме Лагранжа описывают движения индивидуальной частицы жидкости или твердого тела. Уравнения в форме Эйлера описывают  то, что происходит в некотором элементе объема пространства. Рассматриваются силы, скорости, смещения и т.д. применительно именно к этому малому элементу пространства; судьба индивидуальных частиц при этом не важна. На примере реки: Лагранж интересуется движением индивидуальных частиц жидкости, а Эйлер – скоростями и пр. в определенной точке пространства, где одни частицы постоянно сменяются другими.

Задача определения потенциала от движущегося заряда является ярким примером подхода Эйлера. Решается она так:

Для простоты, будем считать, что заряд имеет кубическую форму и точка Р находится прямо по направлению движения заряда, на оси движения. Объем пространства, через который пройдет заряд за то время, пока сигнал от самого дальнего от точки Р элемента заряда путешествовал до самого ближнего элемента, разбивается на элементы толщиной  w.  Суммарный потенциал в точке Р определяется как сумма сигналов от каждого элемента объема, излученных в последовательные моменты времени (разница между которыми  dt = w/c).  Подчеркиваю – от каждого элемента объема, а не элемента заряда. Допустим, для примера, что скорость источника  v = 0.75 c.  Процедура суммирования сигналов такова:

Сначала к сумме добавляется сигнал от самого дальнего элемента объема, где в этот момент находится первый элемент заряда с толщиной  w  и плотностью заряда  ρ.  Потом мы переходим к следующему элементу объема толщиной  w  и добавляем к сумме его сигнал, излученный в момент времени  dt = w/c. За это время, первый элемент заряда успел частично сместиться во второй элемент объема, так что 75% второго элемента объема будут заполнены первым элементом заряда – и он опять вносит вклад в сигнал, который добавляется к общей сумме. Оставшиеся 25% объема второго элемента объема заполнены вторым элементом заряда, так что плотность заряда остается той же самой – ρ.  В следующий момент времени, все тот же первый элемент заряда займет 50% третьего элемента объема – и внесет 50% вклада в сигнал от него; второй элемент заряда тоже внесет 50% вклада. Плотность заряда та же. И т.д.

На следующем рисунке проиллюстрирована эта процедура суммирования для  v = 0.75 c. 

⦾⦾⦾⦾
⎕⎕⎕⎕⦾⦾⦾⦿
⎕⎕⎕⎕⎕⎕⎕⎕⦾⦾⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦾⦿⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿⦿◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿◍◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿◍◍◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕◍◍◍◍

Здесь  ⦾  обозначает 25% первого элемента заряда,  ⦿ - 25% второго элемента заряда,  ◍ - 25% третьего элемента заряда,  ⎕⎕⎕ - элементы объема, которые более не вносят вклад в суммарный потенциал.

Интересно девки пляшут, по четыре сразу в ряд. При такой процедуре суммирования, каждый элемент заряда внесет свой вклад в сигнал не один раз, а 4 раза, потому что он успевает несколько раз «отметиться» в разных элементах объема (вклад всех, кроме первого и последнего элементов заряда, сначала растет от 25% до 100%, потом опять убывает до 25%). В этом и заключается физический смысл уравнения Лиенара-Вихерта. Это уравнение стоит на идее, что суммировать сигнал от заряда надо не по элементам заряда, а по тому объему пространства, через который заряд пройдет за время путешествия сигнала от дальнего конца заряда к ближнему, причем суммирование производится таким образом, что каждый элемент заряда учитывается не один, а много раз.

Я думаю, что намного больше физического смысла имеет иная процедура суммирования (то есть иная процедура взятия интеграла по объему) – по самим элементам заряда. При этой процедуре, каждый элемент заряда вносит вклад в общий потенциал только один раз. Допустим, для  v = 0.9 c,  суммирование будет выглядеть следующим образом:

В первый момент времени, сигнал излучается самым дальним элементом заряда. Во второй момент времени, сигнал излучается вторым элементом заряда, который за это время успел сместиться на расстояние  9w.  В третий момент времени, сигнал излучается третьим элементом заряда, который за это время успел сместиться еще на расстояние  9w.  И так далее. В итоге, каждый элемент заряда внесет свой вклад в суммарный потенциал только один раз и уравнение для потенциала будет, все-таки:

g = f / r’

Для иллюстрации:

◘■■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□■◘■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□■■◘■■□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■◘■□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■■◘

Здесь  ◘ - элемент заряда, который излучает сигнал в данный момент времени,  ■■■ – остальные элементы заряда, сигнал от которых в данный момент не учитывается,  □□□ – элементы пустого пространства.

Приведу еще один аргумент. Я ранее писал:

Любая переменная  f,  для которой можно записать волновое уравнение вида

∂²f/∂t² – c²∇²f = S(x – ξ, y, z, t – ԏ)   

имеет фронты волн, распространяющиеся со скоростью  c.  Производная  f  по  r’  всегда будет приобретать ЛВД множитель  1 / (1– r’∙v / (r’c)), каков бы ни был вид зависимости самой  f  от  r’.

Интересно получается. Производная по расстоянию  r’  обязательно должна приводить к появлению ЛВД множителя (вот здесь это уже несомненно – я сам проверил   :) ). А Лиенар с Вихертом утверждают, что и интеграл по объему (главный вклад в который вносит именно интеграл по направлению  r') – тоже приведет к появлению того же множителя. Как это так? Математические манипуляции, противоположные по смыслу и обычно по своему результату, вдруг приводят к одному и тому же результату?

Иными словами, я утверждаю, что физика пользуется неправильной процедурой интегрирования по объему для процессов, меняющихся  со временем (а также рядом других математических процедур, которые мы рассмотрим позже). Те самые "гениальные дикари" XVIII-XIX веков совершили математические ошибки - и эти ошибки стали фундаментом физики.

Это был сравнительно более простой (совсем без математики не получилось) пересказ некоторых идей, высказанных ранее. На самом деле, это всё пока что затянувшееся введение, всё то же набившее, наверно, оскомину «нулевое приближение». Пора мне переходить уже к действительно интересным вещам – к первому приближению, для начала. Здесь я дам действительно качественную трактовку, на пальцах. Может быть, имеет даже смысл коротко, на пальцах дать общую картину моего видения «новой физики», а также того, в чем я вижу основные ошибки математики и примкнувшей к ней физики. Общий обзор, а потом перейдем к деталям. Попробую.