Тред №579364

Различия между исходными понятиями физики и русики

Есть такое популярное выражение: «Законы физики еще никто не отменял». Как вы понимаете, оно более не соответствует реальности. Потому что именно это я и делаю – отменяю законы физики. Иными словами, аксиомы физики. У русики другие законы (аксиомы). То, что было (или казалось) очевидным в рамках физики, более таковым не является. Это очень сильное утверждение, но означает оно не то, что моя мания величия заходит настолько далеко, что я считаю себя равным Богу-Творцу Вселенной. Нет – я всего лишь утверждаю, что некоторые аксиомы физики неверны и потому практически вся физика ошибочна.

Те аксиомы, о которых шла речь в предыдущей главе, практически совпадают и в классической физике, и в русике. Теперь давайте перейдем к тому, что отличает русику от классической физики. Еще раз – отличия эти чрезвычайно просты и элементарны, примерно на том же уровне сложности, как  перенесение  bⁿ  в правую часть уравнения Ферма. Я об этом предупреждал с самого начала (кто не спрятался, я не виноват).

В классической физике ключевую роль играют понятия «система отсчета», Принцип Относительности Движения Галилея и Второй Закон Ньютона (не буду приводить их определения, чтобы не загромождать текст). Вместо них, в русике ключевую роль играют понятие «среда отсчета», Принцип Дуализма Движения и Принцип Аберрации.

В физике, движение какого-либо тела или волны можно равноправно описать в разных системах отсчета, двигающихся друг относительно друга с разными скоростями. Каждая система отсчета имеет свою собственную систему координат – x₁, y₁, z₁ , или x₂, y₂, z₂, или x₃, y₃, z₃, и т.д. – в которых и описывается движение тела или волны. Подчеркну, что в физике для описания движения достаточно только одной системы отсчета и связанной с ней системы координат.

В русике, постулируется, что любое движение тела или волны всегда происходит сквозь какую-то среду (поскольку пустого пространства не существует), и этим движением относительно среды нельзя пренебрегать, оно не сводится к движению тела или волны относительно наблюдателя. Назовем среду, сквозь которую движется наблюдаемое тело или волна, «средой отсчета». Во многих задачах русики встречаются разные среды (чьи свойства, например, плотность, могут различаться), а кроме того, разные элементы среды движутся с разными скоростями, так что имеет смысл использовать термин «элемент среды отсчета» (ЭСО). Каждый ЭСО имеет свою внутреннюю систему координат, причем оси координат не уходят в бесконечность, а имеют конечные размеры, совпадающие с размерами ЭСО.

Русика, далее, постулирует, что любое движение всегда состоит из двух отдельных компонент: движение наблюдаемого тела или волны относительно ЭСО, в его внутренней системе координат, и движение этого ЭСО относительно системы отсчета наблюдателя (СОН), в системе координат, привязанной к данной СОН. В этом и заключается Принцип Дуализма Движения. Во избежание двусмысленности или непонимания, подчеркну, что первый компонент (движение наблюдаемого тела или волны относительно ЭСО) означает, что ЭСО считается покоящимся, а наблюдаемое тело или волна движется относительно него.

Аксиома 7 (Принцип Дуализма Движения): Движение любого тела или волны относительно наблюдателя состоит из двух независимых компонентов: движения наблюдаемого тела или волны относительно элемента среды отсчета и движения элемента среды отсчета относительно наблюдателя.

Теперь нам надо придумать подходящие термины для обозначения этих двух видов движения. Я долго ломал голову (и язык) над разными вариантами и в конце концов пришел к выводу, что надо воспользоваться классическим способом создания новых научных терминов – использовать древнегреческий или латынь. Пусть будет латынь.

На латыни, «относительно наблюдателя» будет «relative ad aspicientis», «относительно среды» – «relative ad medium», а «сквозь среду» – «per medium». Думаю, для краткости можно убрать «relative» и оставить только «ad aspicientis» (к наблюдателю), а вместо «ad medium» (к среде) лучше использовать «per medium» (сквозь среду), поскольку тело движется именно сквозь среду, а не к ней.

Принципиально важно, что движение тела или волны per medium все наблюдатели описывают одинаково, оно, можно сказать, является абсолютным, и только движение ЭСО ad aspicientis выглядит по-разному для разных наблюдателей, то есть является относительным (в том же смысле, как относительность употребляется в физике). Иными словами, движение per medium объективно, а движение ad aspicientis – субъективно. В физике, напомню, любое движение относительно, то есть субъективно.

Какими буквами нам обозначить координаты ЭСО и СОН? Ранее я использовал  x, y, z  для обозначения системы координат некой системы отсчета и  ξ, η, ζ  для обозначения координат источника волн в этой системе отсчета. Давайте будем использовать большие буквы  X, Y, Z  для обозначения внутренних координат ЭСО (большие буквы как раз подчеркивают абсолютный, или объективный, характер движения относительно этих координат). Оси  X, Y, Z, разумеется, не обязаны совпадать с осями  x, y, z.  Если таких элементов у нас будет много, то их внутренние координаты будут с индексами:  X₁, Y₁, Z₁,  X₂, Y₂, Z₂,  X₃, Y₃, Z₃,  и т.д.

Опять же во избежание двусмысленности и непонимания, подчеркну, что, например, векторы скорости движения тела per medium и скорости движения ЭСО ad aspicientis не складываются в один суммарный вектор. Правило сложения векторов здесь не применяется. Это два независимых вектора и они оба необходимы для описания движения тела. То же касается и векторов позиции тела внутри ЭСО и позиции этого ЭСО в некой СОН: вектора не складываются, они оба необходимы для описания движущегося тела (или волны). Аналогично для ускорений: каждому движущемуся тел соответствуют два вектора ускорения – вектор ускорения тела относительно ЭСО и вектор ускорения данного элемента относительно СОН.

Как это обозначить математически? Вместо одного вектора скорости, как в физике, мы имеем два: вектор скорости наблюдаемого тела per medium  V(V_X, V_Y, V_Z)  и вектор скорости ЭСО ad aspicientis  v(v_x, v_y, v_z).  Обозначим их как «двойной вектор» с 6 компонентами:  V⨁v(V_X, V_Y, V_Z, v_x, v_y, v_z).  В принципе, этот двойной вектор можно было бы представить и в виде матрицы вида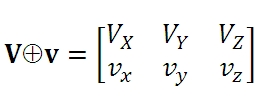
 

 
Эта матрица похожа на тензор, но им не является, поскольку верхняя и нижняя строчки данной матрицы ведут себя совершенно по-разному при переходе от одной системы отсчета к другой: верхняя строчка выглядит одинаково для всех наблюдателей, а вот нижняя строчка у разных наблюдателей отличается. У тензора же при переходе от одной системы отсчета к другой должны измениться компоненты и верхней, и нижней строчки матрицы.

Речь здесь идет только о форме записи, об обозначениях. Наверно, запись в виде матрицы с двумя строчками лучше не использовать, чтобы не было путаницы с тензорами. Будем пока использовать двойные векторы с 6 компонентами в одной строке – как V⨁v(V_X, V_Y, V_Z, v_x, v_y, v_z).

Еще раз, я не математик и не претендую на исключительное знание математики – несмотря на то, что я утверждаю, что физика неверна именно потому, что она использует неверную математику. Но я шел к пониманию этого со стороны физики, а не математики. Так что я знаком далеко не со всеми обозначениями математических понятий (да и с самими понятиями, чего греха таить…). В физике, понятие двойных векторов мне не встречалось. Если же и в математике оно отсутствует, то русика потребует создания нового раздела математики. Здесь есть математики? Буду благодарен за экспертное мнение.

В отличие от русики, физика использует не два вектора  V  и  v  по отдельности, а только их векторную сумму  V + v  c 3 компонентами (V_X + v_x, V_Y + v_y, V_Z + v_z). Это равнозначно использованию вместо отдельных компонент вектора (a, b, c) только скалярной длины этого вектора  (a² + b² + c²)^½,  или, вместо 9 компонент тензора напряжений, использованию обычного вектора с 3 компонентами, просуммировав значения столбиков матрицы. Как следствие этого неоправданного упрощения, физика «не видит» многих особенностей движения и приводит к ложным выводам (а русика всёёёоооооо видит…).

Разумеется, и в русике мы можем определить векторную сумму V + v  и использовать ее в каких-то задачах. Подобно этому, зная (x, y, z) компоненты какого-то вектора, можно определить его длину, в ряде задач она нужна. Но если вы знаете только длину вектора, ваши знания о нем весьма неполны и очень многого о поведении исследуемой вами системы вы не узнаете.

Далее, вместо одного радиус-вектора, описывающего позицию движущейся материальной точки, мы имеем два вектора  R(X, Y, Z)  и  r(x, y, z).  Их двойной вектор будет   R⨁r(X, Y, Z, x, y, z).  Аналогично, два вектора ускорений  A(A_X, A_Y, A_Z)  и  a(a_x, a_y, a_z)  образуют двойной вектор  A⨁a(A_X, A_Y, A_Z, a_x, a_y, a_z).  Так же со всеми векторами.

О математических манипуляциях над двойными векторами, в частности, о действии на них различных операторов, я буду говорить позже.