Тред №581581

Картины в масле 3

Дробинки – маленькие и круглые, практически материальные точки. Для следующего эксперимента выберем арбалет с продолговатыми стрелами (болтами). Диспозиция точно такая же: космонавт Вася стоит рядом с бруском масла М₁, мимо которого двигается брусок М₂ и стреляет в сторону М₁ в момент времени  t₁.

В момент времени  t₂,  болт достигает конца бруска М₁ и входит в брусок М₂. На следующем рисунке изображена внутренняя скорость болта  V₁(V_X₁, V_Y₁, V_Z₁) в среде отсчета М₁:
 

 
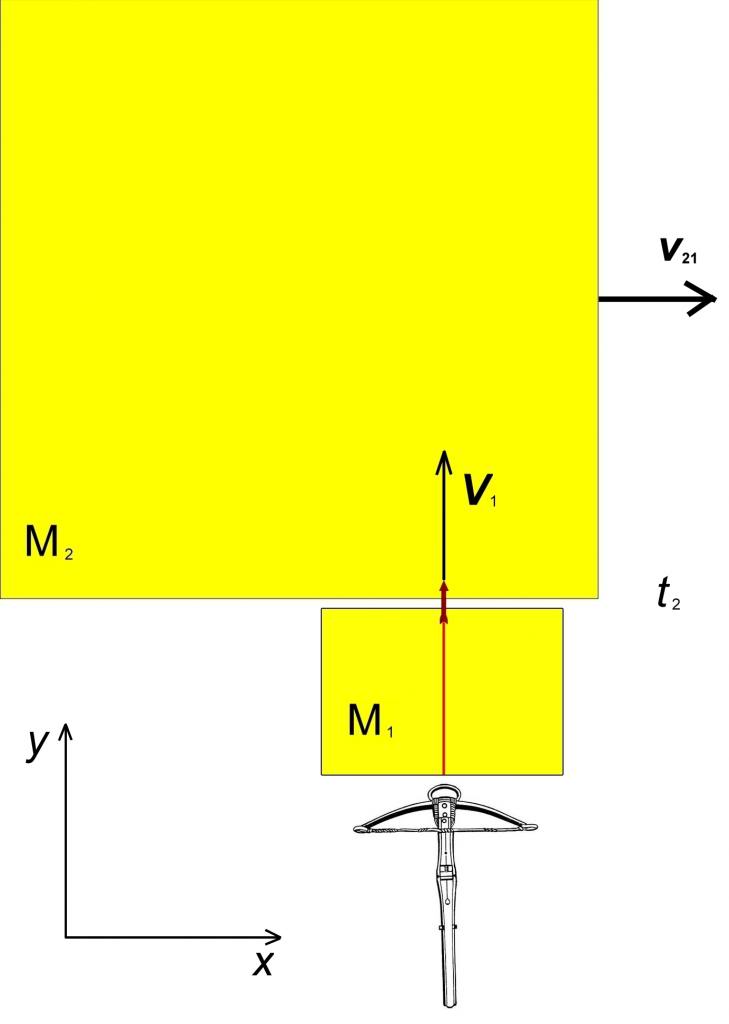
Болт – это темно-красная стрелка. Отметим, что согласно Аксиоме 8 в момент  t₂  и болт, и оба бруска будут выглядеть одинаково для всех наблюдателей. То есть болт будет направлен по оси  y  и относительно среды отсчета М₁, и относительно среды отсчета М₂.

Внутренняя скорость болта относительно среды отсчета М₂ в момент его входа в М₂ станет равна

V₂ (V_X₂, V_Y₂, V_Z₂) = V₁(V_X₁, V_Y₁, V_Z₁) –  v₂₁

То есть болт войдет в среду М₂ не в направлении оси  y,  как он двигался сквозь среду М₁, а под углом к ней (вектор  V₂):
 

 
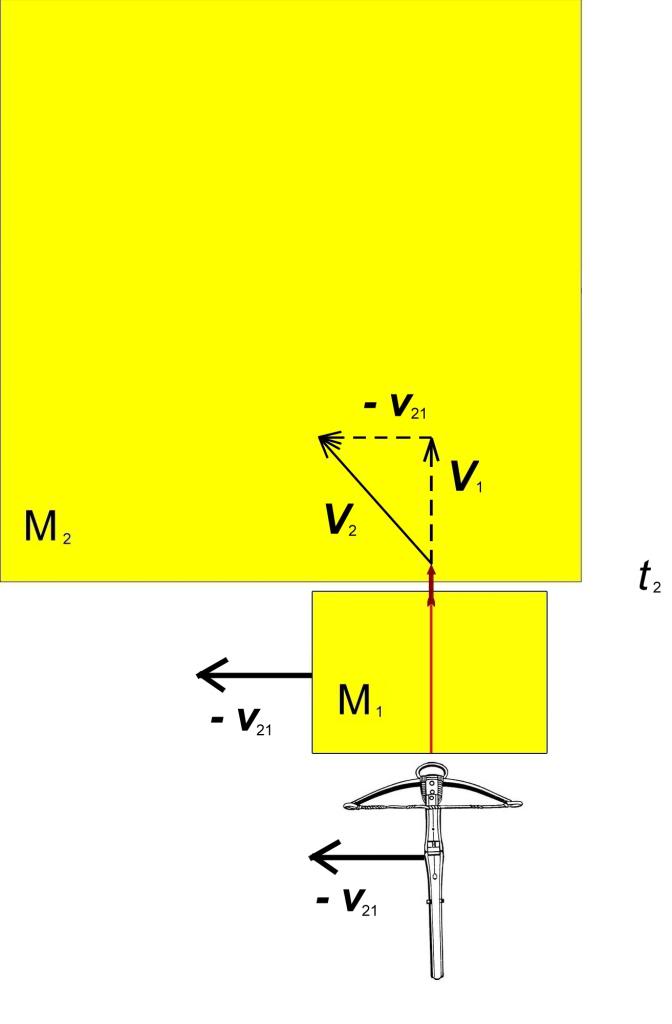
Обратите внимание, болт будет двигаться относительно среды М₂ не таким, аэродинамически выгодным способом:
 

 
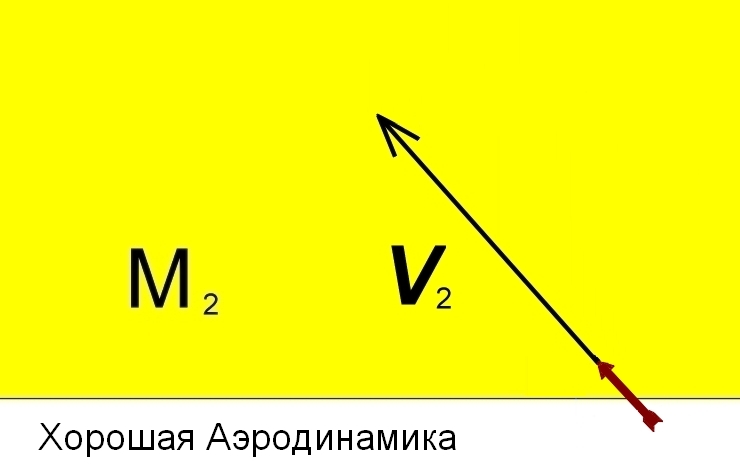
А вот так (боком):
 

 
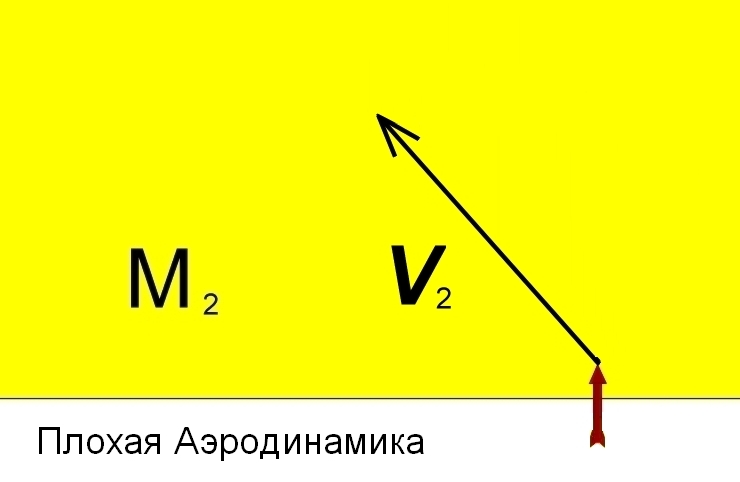
То есть на острие болта будет действовать сила в направлении, противоположном вектору V₂, разворачивая его по часовой стрелке, так что болт начнет «кувыркаться». Это еще один пример того, что силы, действующие на тело, определяются именно его движением сквозь среду. Именно это я имел в виду, когда ранее писал, что движение тела (и волны, о чем чуть позже)  per medium  является абсолютным и объективным, а движение  ad aspicientis  является относительным и субъективным.

Из этих картин с дробинками и арбалетным болтом в масле можно сделать ряд практических выводов. Их, впрочем, вполне можно сделать и в рамках физики (физика ведь отнюдь не возбраняет переход из одной системы отсчета в другую), но у меня такое впечатление, что далеко не всегда эти выводы применяются на практике.

Например, как должен лететь самолет из пункта А в пункт Б, если между этими пунктами дует боковой ветер? Русика сразу и однозначно говорит, что самолет должен быть развернут в направлении вектора  V₂  на рисунке, подписанном «Хорошая Аэродинамика». В реальности же, не скажу всегда, но как правило, судя по моему опыту полетов на самолетах, самолеты при наличии бокового ветра не меняют свою ориентацию в пространстве. Есть ветер, нет ли, но самолет будет ориентирован как на рисунке, подписанном «Плохая Аэродинамика». Только, в отличие от арбалетного болта, самолет может сопротивляться своему развороту ветром, что он и делает, удерживая свою ориентацию в пространстве. А чтобы самолет не сносило ветром и он прилетел именно туда, куда нужно, тяга двигателей будет направлена как раз в направлении вектора  V₂.  Замечательно – всё время полета в условиях бокового ветра самолет (относительно среды, т.е. движущегося воздуха) летит боком. И расход топлива больше, и нагрузки на самолет такие, что он намного скорее выйдет из строя.

Таких примеров можно привести много, но я предпочитаю перейти наконец к волнам и силам. Потому что наиболее важные приложения Принципа Аберрации я вижу не в механике, а в электродинамике и волновой механике. Я достаточно подробно остановился на примерах применения этого принципа в механике только потому, что здесь его можно объяснить очень просто и наглядно. После такого объяснения, я надеюсь, понять Принцип Аберрации Волн будет намного легче.