Тред №596170

б) Луч 2

Пусть два последовательных фронта волны падают на границу раздела между М₁ и М₂ под углом  ψ.  В элементе М₁, расстояние между фронтами равно  λ₁.  Это длина отрезка |HA|. Фронт 1 касается границы раздела в точке А / A' (принадлежащих, соответственно, элементам М₁ и М₂), фронт 2 – в точке Е / E’.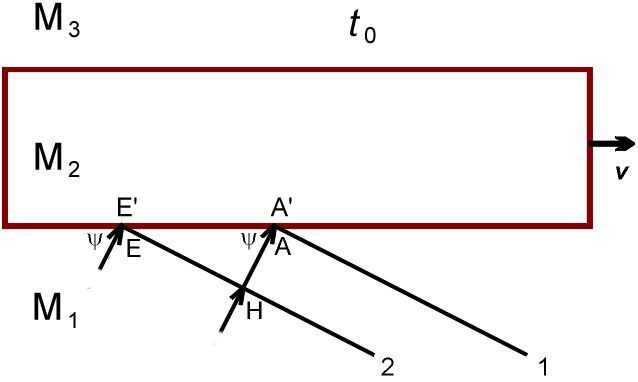
 

 
Через промежуток времени  ∆t = λ₁/c,  фронт 2 займет место фронта 1 в элементе М₁. За это время, элемент М₂ сдвинется вправо на расстояние  v∆t,  в том числе сдвинутся точки A’ и E’. Согласно Принципу Гюйгенса (в формулировке Аксиомы 10), точки A' и E' станут источниками вторичных сферических волн, распространяющихся в элементе М₂. Радиус этих волн будет равен λ₁, то есть равен расстоянию между фронтами волн 1 и 2 в элементе М₁.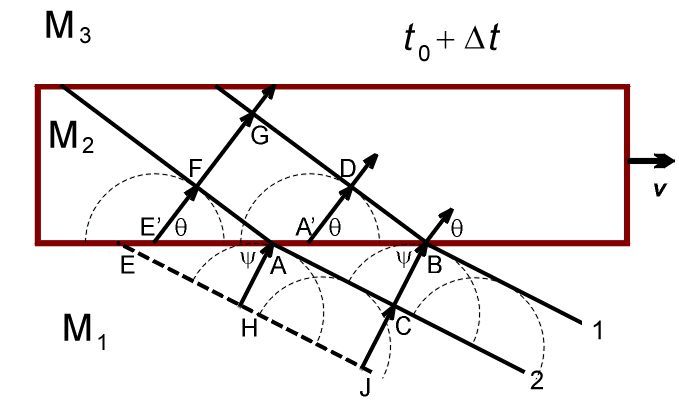
 

 
Чтобы получить фронт волны 1 в элементе М₂, мы должны соединить точки B и D, фронт волны 2 – точки A и F. Соответствующие лучи перпендикулярны этим фронтам. Мы видим, что угол  θ  между направлением луча внутри М₂ и границей раздела изменился, по сравнению с углом  ψ  (между направлением этого луча внутри М₁ и границей раздела). Произошла аберрация звука – но, что обращает на себя внимание, прямо противоположно аберрации света. Лучи звука отклоняются в том направлении, в котором двигается элемент М₂, а лучи света от звезд отклонялись в направлении, противоположном движению Земли вокруг Солнца. Мы к этому еще вернемся, после того как закончим со звуком.

Из простых геометрических соображений, мы можем легко получить зависимость между  θ, ψ  и  v:

cos θ = 1/(1/cosψ – v/c)

Поскольку два года назад, когда я писал много формул с подробным выводом (очень простых, но тем не менее), это, как выяснилось, только отпугивало большинство читателей, я буду сейчас, по возможности, стараться ограничиться качественными рассуждениями, на пальцах. Я также буду прятать под спойлер некоторые формулы и их вывод.

cosθ = |E’F|/|E’A|

|E’F| = λ₁

|E’A| = |EA| – |EE’| = |HA|/cosψ – vΔt = λ₁/cosψ – λ₁ v/c

cosθ = λ₁/( λ₁/cosψ – λ₁ v/c) = 1/(1/cosψ – v/c)


Аналогично, мы можем определить, как изменится расстояние между фронтами 1 и 2 в элементе М₂ по сравнению с этим расстоянием в элементе М₁  (т.е.  λ₁):

λ₂ = λ₁ (1 + (v/c) cosθ) = λ₁ / (1 – (v/c) cosψ)

Частоты волн будут связаны соотношением:

ω₂ = ω₁ (1 – (v/c) cosψ)

Эти формулы, разумеется, применимы и к лучу 1 (поперечному): подставив  ψ = 90°,  мы получим  θ = 90°,  λ₂ = λ₁  и  ω₂ = ω₁.

Вернемся к лучу 2. Пройдя сквозь всю толщину элемента М₂, фронты 1 и 2 достигнут границы раздела с элементом М₃, где опять произойдет аберрация звука.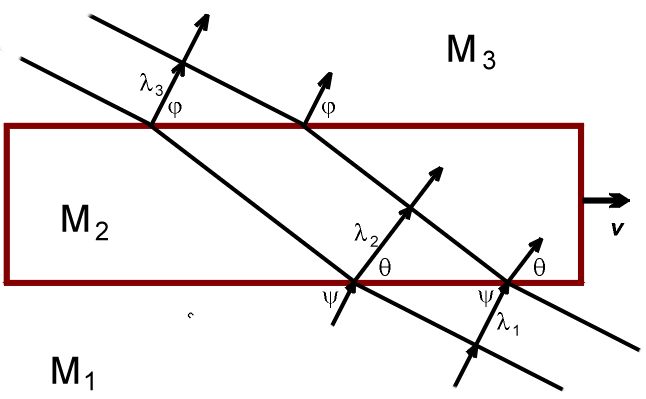
 

 
Повторив несложные манипуляции, мы увидим, что  φ,  угол между направлением луча в элементе М₃ и границей раздела с М₂, равен  ψ,  аналогичному углу в элементе М₁, а  λ₃, расстояние между фронтами 1 и 2 в элементе М₃, равно  λ₁, аналогичному расстоянию в элементе М₁:

cosφ = 1/(1/cosθ + v/c) = cosψ

λ₃ = λ₂ (1 – (v/c) cosφ) = λ₁ (1 – (v/c) cosφ) / (1 – (v/c) cosψ) = λ₁

Что видно и из рисунка.

в) Луч 3

При определенном критическом угле  ψ₀,  аберрация луча будет столь велика, что угол θ будет равен 0° и луч в элементе М₂ будет параллелен границе раздела с элементом М₁: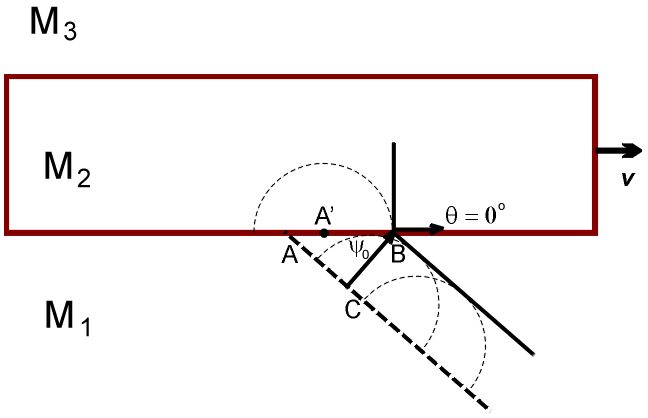
 

 
Подставив  θ = 0°  в уравнение  cos θ = 1/(1/cosψ – v/c),  мы получим

cosψ₀ = 1/(1 + v/c)

Это произойдет, когда расстояние |A’B| равно  c∆t,  так что

|AB| = |AA’| + |A’B| = vΔt + c∆t

г) Луч 4

Все лучи с углами падения меньше  ψ₀  будут отражаться от границы раздела М₁ и М₂: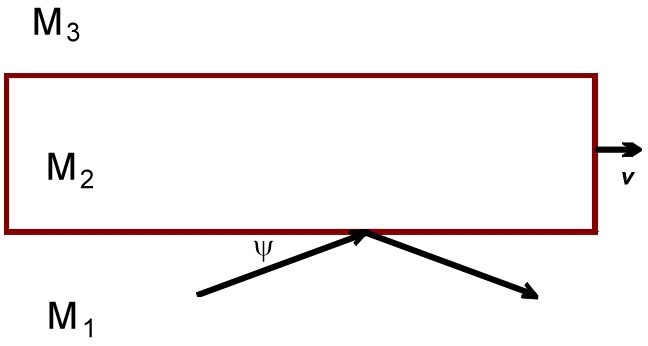
 

 
Казалось бы, это тривиально – но это будет играть важную роль в искривлении лучей от движущихся источников.