Тред №603531

«Красное Смещение» Звука

Выше мы рассмотрели аберрацию звука в элементе среды М₂, скорость которого относительно элемента М₁ была параллельна разделяющей их границе: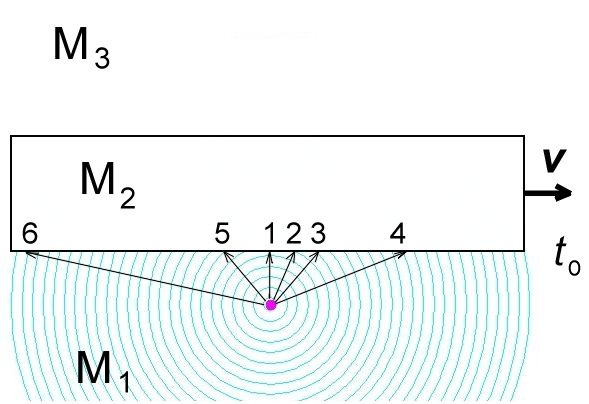
 

 
Разумеется, относительные скорости элементов могут быть направлены как угодно, совсем не обязательно параллельно (или перпендикулярно) границе между ними. Однако, поскольку анализ распространения волн во множестве движущихся элементов среды возможен, в большинстве случаев, лишь численно, при помощи компьютеров, и поскольку, по определению, эти элементы двигаются и непрерывно меняют свои позиции друг относительно друга, то имеет смысл на каждом шагу вычислений переопределять границы этих элементов. А раз так, то желательно выбирать эти границы таким образом, чтобы это облегчало вычисления. Логично, в частности, выбирать границы между соседними элементами так, чтобы они были параллельны или перпендикулярны относительным скоростям их движения. Еще раз, это не фундаментальное правило, а просто способ облегчения вычислений. Компьютер, впрочем, справился бы с любыми, даже очень громоздкими, уравнениями; эра вычислений столбиком или на логарифмической линейке все-таки в прошлом. Я об этом упоминаю лишь потому, что когда мы с моей дочерью Валей обсуждали, как составлять программы для численного анализа распространения волн (этим занималась в основном она), мы пришли к выводу, что на каждом шагу вычислений новые границы элементов следует выбирать именно параллельно или перпендикулярно относительным скоростям этих элементов.

Параллельный случай мы уже разобрали. Займемся теперь перпендикулярными случаями, когда лучи падают на границу с движущимся элементом среды вдогонку или навстречу ему, то есть когда два элемента среды удаляются друг от друга или приближаются друг к другу: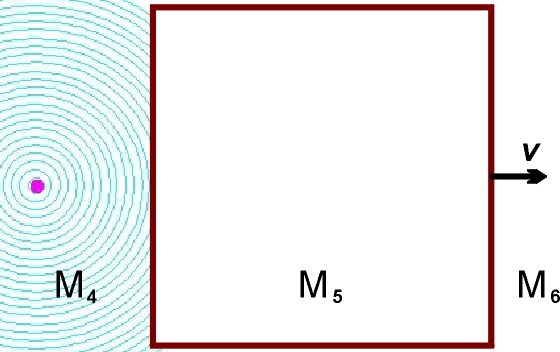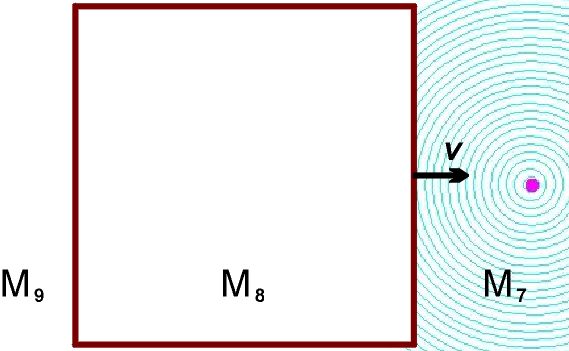
 

 

 
Элементы М₄ и М₆, М₇ и М₉ покоятся друг относительно друга (подобно элементам М₁ и М₃). На рисунках ниже эти элементы повернуты на 90 градусов; так было удобнее рисовать. Надеюсь, никакой путаницы это не вызовет.

а) Удаляющиеся Элементы

Метод анализа все тот же (при помощи Принципа Гюйгенса в формулировке Аксиомы 10). Пусть два последовательных фронта волны падают на границу раздела между М₄ и М₅ под углом  ϕ.  В элементе М₄, расстояние между фронтами равно  λ₄.  Фронт 1 касается границы раздела в точке А / A' (принадлежащих, соответственно, элементам М₄ и М₅), фронт 2 – в точке Е / E’.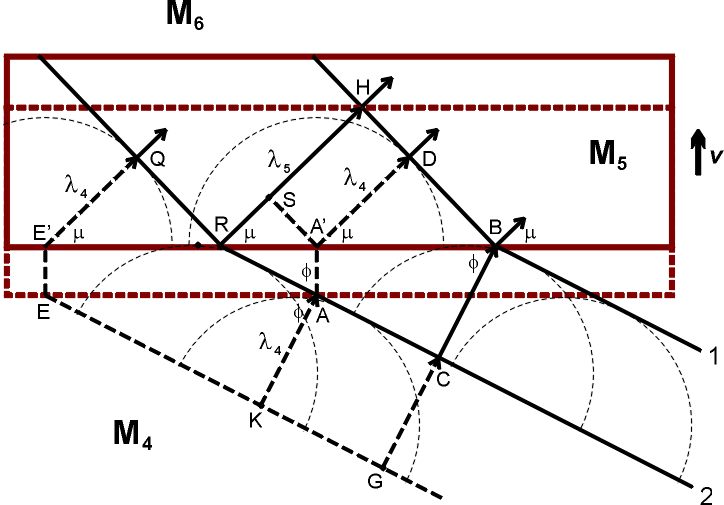
 

 
Через промежуток времени  ∆t = λ₄/c,  фронт 2 займет место фронта 1 в элементе М₄. За это время, элемент М₅ сдвинется вверх на расстояние  v∆t,  в том числе сдвинутся точки A’ и E’, ставшие источниками вторичных сферических волн радиуса  λ₄  в элементе М₅. Чтобы получить фронт волны 1 в элементе М₅, соединим точки B и D, фронт волны 2 – точки R и Q.

Аналогично тому, как это было сделано для «параллельного» случая, мы можем получить соотношение между углами  μ  и  ϕ, а также длинами волн  λ₅  и  λ₄:

cosμ = cosϕ / (1 – (v/c) sinϕ)

λ₅ = λ₄ / (1 – (v/c) sinϕ)

Вывод:

cosμ = |A’D| / |A’B|
|A’D| = λ₄ = cΔt
|A’B| = |RB| – |RA’|
|RB| = |CB| / cosϕ = cΔt / cosϕ
|RA’| = |AA’| tgϕ = vΔt sinϕ / cosϕ
|A’B| = cΔt (1 – (v/c) sinϕ) / cosϕ
cosμ = cΔt / (cΔt (1 – (v/c) sinϕ) / cosϕ) = cosϕ / (1 – (v/c) sinϕ)

|RB| = |RH| / cosμ = |CB| / cosϕ
|RH| = λ₅           |CB| = λ₄
λ₅ = λ₄ cosμ / cosϕ = λ₄ / (1 – (v/c) sinϕ)


Частоты волн будут связаны соотношением:

ω₅ = ω₄ (1 – (v/c) sinϕ)

б) Приближающиеся Элементы

Теперь звуковые волны со стороны элемента М₇ падают на элемент М₈, который приближается к М₇ со скоростью v: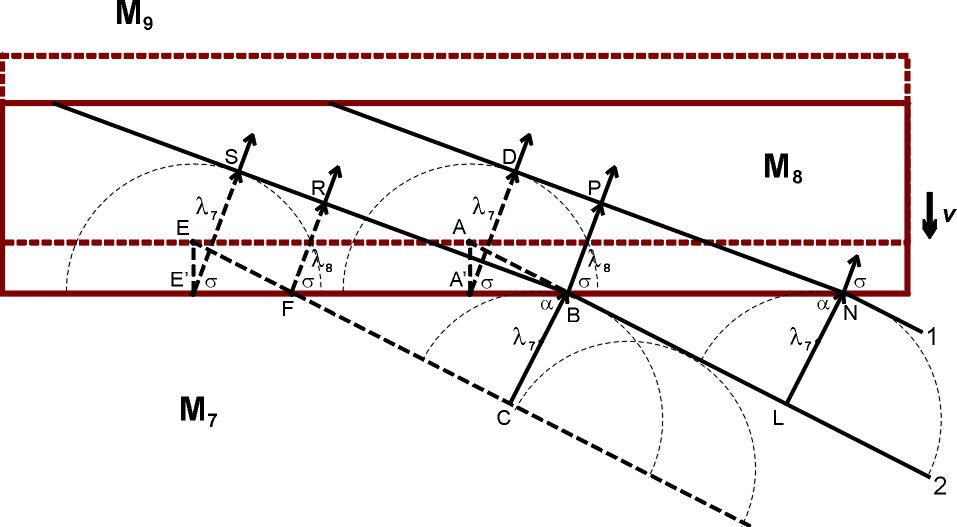
 

 
Повторив те же самые геометрические манипуляции, мы получим следующие уравнения:

cosσ = cosα / (1 + (v/c) sinα)

λ₈ = λ₇ / (1 + (v/c) sinα)

ω₈ = ω₇ (1 + (v/c) sinα)

Это, в общем-то, вполне логично: по сравнению с удаляющимся элементом М₅, минус меняется на плюс, что отражает направление движения элемента М₈.

Далее, нас интересует, что произойдет с лучами, когда они пройдут сквозь всю толщину элемента М₈ и выйдут в элемент М₉.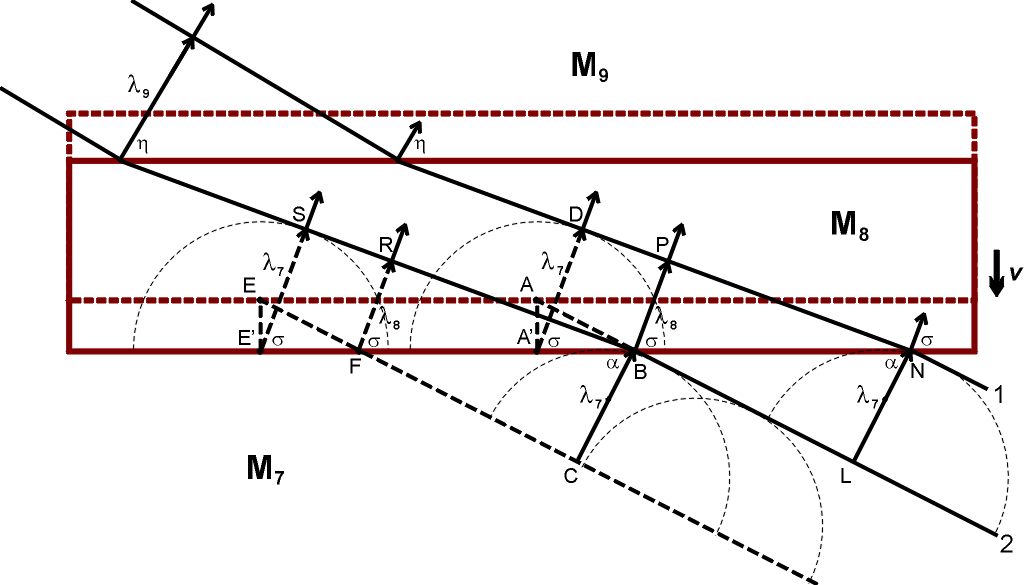
 

 
Нет ничего проще: поскольку элемент М₉ удаляется от элемента М₈, мы просто должны применить формулы, полученные выше для перехода лучей из М₄ в М₅:

cosη = cosσ / (1 – (v/c) sinσ) = cosα / ((1 – (v/c) sinσ)(1 + (v/c) sinα))

λ₉ = λ₈ / (1 – (v/c) sinσ) = λ₇ / ((1 – (v/c) sinσ)(1 + (v/c) sinα))

ω₉ = ω₇ (1 – (v/c) sinσ)(1 + (v/c) sinα)


Вообще говоря, мы можем в этих уравнениях вместо sinσ подставить

sinσ = (1 – cos²σ)½ = (1 – cos²α / (1 + (v/c) sinα)²)^½

Но это непринципиально.


Что здесь важно: угол  η  не равен углу α,  а длина волны  λ₉  не равна длине волны  λ₇.  То есть пройдя сквозь элемент среды М₈, двигающийся навстречу элементу М₇ и выйдя в элемент М₉, неподвижный относительно М₇, луч звука изменит свое направление. Напомню, что в «параллельном» случае угол  φ  в элементе М₃ был равен углу ψ  в элементе М₁, а длина волны  λ₃  была равна длине волны λ₁.  (прохождение луча звука сквозь элемент М₂ вызывало лишь небольшой сдвиг в направлении движения элемента М₂).

Стоит подчеркнуть, что длина волны  λ₉  всегда будет больше длины волны  λ₇.


Поскольку  v ≪ c,  мы можем приближенно записать

λ₉ ≈ λ₇ (1 + (v/c) sinσ)(1 – (v/c) sinα) ≈ λ₇ (1 + (v/c) (sinσ – sinα))

Но  sinσ  всегда больше, чем  sinα  (см. рисунок). Следовательно,  λ₉  всегда будет больше  λ₇  (хотя и чуть-чуть).


а’) Удаляющиеся Элементы

Аналогичным образом, мы можем получить уравнения для лучей, которые пройдут сквозь весь элемент М₅ и выйдут в элемент М₆.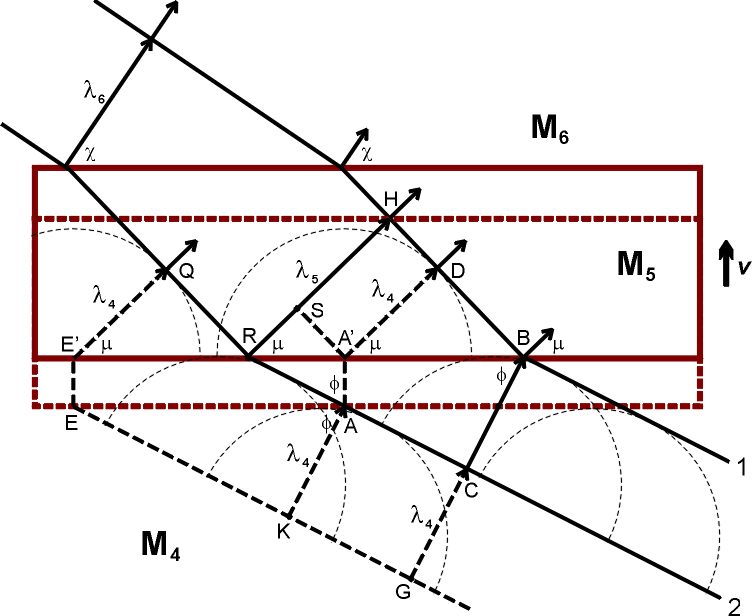
 

 
Здесь мы применим формулы перехода лучей из М₇ в М₈:

cosχ = cosμ / (1 + (v/c) sinμ) = cosϕ / ((1 + (v/c) sinμ)(1 – (v/c) sinϕ))

λ₆ = λ₅ / (1 + (v/c) sinμ) = λ₄ / ((1 + (v/c) sinμ)(1 – (v/c) sinϕ))

ω₆ = ω₄ (1 + (v/c) sinμ)(1 – (v/c) sinϕ)

Здесь также угол  χ  не равен углу ϕ,  а длина волны  λ₆  не равна длине волны  λ₄.  Но что особенно интересно, длина волны  λ₆  всегда будет больше длины волны  λ₄ – точно так же, как это было с  λ₉  и  λ₇.


При  v ≪ c,

λ₆ ≈ λ₄ (1 – (v/c) sinμ)(1 + (v/c) sinϕ) ≈ λ₄ (1 + (v/c) (sinϕ – sinμ))

Но  sinμ  всегда меньше, чем  sinϕ  (см. рисунок). Следовательно,  λ₆  всегда будет чуть-чуть больше  λ₄.


Это означает, что звуковые волны от разных источников звука взаимодействуют, вызывая изменение направления лучей звука и увеличение длины волны («красное смещение» звука). Это легко понять, глядя на следующую картинку: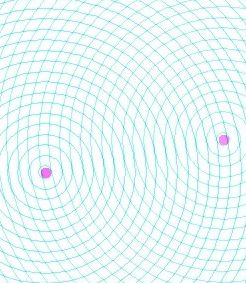
 

 
Лучи от одного источника звука (S₁), проходя через среду, которая приведена в движение волнами от другого источника звука (S₂), будут последовательно проходить то сквозь элементы среды, двигающиеся от S₂, то сквозь элементы среды, двигающиеся к S₂. И каждый раз длина волны луча от S₁ будет чуть-чуть увеличиваться, а направление луча чуть-чуть меняться. Лишь чуть-чуть – но это должно быть вполне измеримо.

В физике есть одно хорошее правило. Новая теория, чтобы быть признанной, должна не только предложить иную интерпретацию ранее известных фактов, которые имели свое объяснение в рамках старой теории. Этого мало – она также должна предсказать хоть какие-то явления, которые отличаются от предсказаний старой теории и которые можно проверить экспериментально. Именно к этой категории относятся предсказания русики насчет «красного смещения» и отклонения лучей звука вследствие взаимодействия звуковых волн от разных источников. Физика, насколько я понимаю, ничего подобного не предсказывает? Ей это явление неизвестно? Замечательно.

Красное Смещение Света от Звезд

Логично предположить, что красное смещение света от далеких галактик может вызываться подобными причинами. Здесь есть, однако, некоторые сложности. Во-первых, я ранее писал, что аберрация звука происходит совсем не так, как аберрация света. Во-вторых, свет, как принято считать, это поперечные волны, а звук – продольные.

Забегая вперед, замечу, что аберрация света происходит прямо противоположно аберрации звука потому, что свет (и эфир) не увлекается веществом. Совсем. Если кто-то забеспокоится, как же тогда объяснить, скажем, опыт Физо, то спешу успокоить – никаких проблем. Все будет объяснено, но чуть позже. Сначала я хочу закончить со звуком (следующий раздел будет об искривлении лучей звука от движущегося источника).

Так вот, поскольку свет от далеких галактик распространяется и взаимодействует между собой в эфире, а не в веществе, то аберрация света в веществе (например, в телескопе) не имеет к этой проблеме никакого отношения. Волны света, распространяясь в эфире, приводят его в движение – и аберрация лучей света в движущихся элементах эфира подчиняется тем же правилам, как и аберрация лучей звука в движущихся элементах газа или жидкости.

Теперь о поперечных волнах. Чем они, собственно, отличаются от продольных волн? Тем, что элементы среды двигаются перпендикулярно направлению распространения волн, то есть перпендикулярно лучам. Но они двигаются! Двигаются элементы струны или мембраны, двигаются элементы воды при распространении волн на поверхности воды, двигаются элементы цилиндрического стержня при крутильных колебаниях. Это главное.

Так же будут двигаться и элементы эфира, приводимые в движение волнами света. Галактики расположены в космосе во всех возможных направлениях, так что свет от любой звезды всегда будет проходить сквозь элементы эфира, двигающиеся либо по направлению к этой звезде (под углом), либо от нее. Длина волны света будет при этом увеличиваться лишь чуть-чуть; но за миллиарды лет путешествий лучей света эти изменения накапливаются и становятся вполне заметными. По результатам наблюдений в 2005 году значение постоянной Хаббла принято равным (72±3) км/(сек•Мпк).

Так что никакого расширения пространства Вселенной нет. В русике, то есть. В физике – пусть будет.