Тред №611517

ЭМ-М 2

Итак, полный вывод уравнения для угла аберрации отражения  α.  Сначала, отметим, что Майкельсон и Морли тоже использовали термин «аберрация», когда они говорили о луче света, отраженном от зеркала  а:

Предположим теперь, что эфир находится в покое и что весь аппарат движется в направлении  sc  со скоростью Земли по ее орбите, тогда направления и расстояния, проходимые лучами, будут меняться таким образом: луч  sa  отражается вдоль  ab  рис. 2  (угол  bab₁  равен аберрации  α),  возвращается вдоль  ba₁  (aba₁ = 2α)  и идет в фокус телескопа, направление которого остается неизменным. Луч, прошедший сквозь стекло, идет вдоль  ас,  возвращается вдоль  ca,  и отражается в  a₁,  делая  ca₁e  равным  90 – α  и, таким образом, вновь совпадая с первым лучом.

И это совершенно правильный термин (с позиции русики; физика, вообще-то говоря, называет аберрацией совершенно другое явление). Интересно, что во всех учебниках по теории относительности, которые я просмотрел, не только не используется термин аберрация, но вообще не объясняется, почему в системе отсчета неподвижного эфира лучи света должны отражаться от движущегося полупрозрачного зеркала, расположенного под углом 45 градусов, не прямо вверх, согласно правилу «угол падения равен углу отражения», а под другим углом. Например, на рисунке из Фейнмановских Лекций По Физике, Т. 2, стр. 9, в системе отсчета лаборатории, где интерферометр покоится, лучи от источника А падают на зеркало В, расположенное под углом 45 градусов, и отражаются вертикально вверх (угол падения 45° равен углу отражения 45°), так что угол АВС равен 90°. На том же рисунке изображен и путь этого луча в  системе отсчета покоящегося эфира: A → B → C’. Здесь угол CBC’ и есть угол аберрации. Но ни слова о том, откуда этот угол взялся, в книге нет.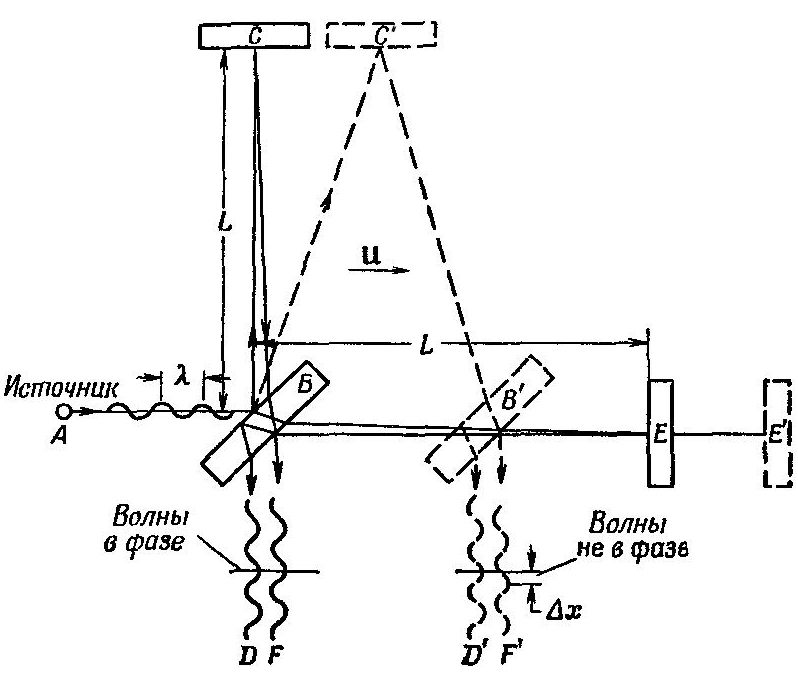
 

 
Я ни в коем случае не хочу сказать, что Фейнман и другие авторы книг по СТО пытаются что-то скрыть. Ничего подобного – я уверен, что большинство физиков верят в справедливость СТО, потому что не видят в ней никаких ошибок (я и сам в нее верил, когда я был студентом ФТФ НЭТИ). Я всего лишь обращаю ваше внимание на то, что если в системе отсчета покоящегося эфира угол падения луча на движущееся зеркало не равен углу его отражения, то это требует, во-первых, некоторого обоснования, а во-вторых, строгого математического вывода формулы для соотношения этих углов. Ничего этого не было сделано не только Майкельсоном и Морли, но и всеми последующими физиками, анализировавшими ЭМ-М.

Таким обоснованием может быть Принцип Гюйгенса, сомнений в котором, я надеюсь, ни у кого нет. Будем использовать его в такой формулировке:

Каждая точка двигающегося зеркала, на которую падает фронт волны света, является источником вторичных сферических волн, распространяющихся в покоящемся эфире со скоростью света. Поверхность, касательная ко всем вторичным волнам, представляет собой волновой фронт в следующий момент времени.

Пусть в момент  t₀  на зеркало  a,  расположенное под углом 45 градусов к лучам света, падает волновой фронт 1, который касается зеркала в точке Е (штрихованная светло-синяя линия). Через промежуток времени  Δt,  этот фронт сдвинется вправо на расстояние   λ₁ = c Δt   (светло-синяя линия), а зеркало  а  сдвинется вправо на расстояние   λ₁ v/c.  Согласно Принципу Гюйгенса, точка E станет источником вторичной сферической волны радиуса  λ₁  (штрихованная красная окружность). Чтобы получить фронт отраженной волны 1’ (темно-синяя линия), нам надо провести касательную линию между точкой H, в которой падающий фронт 1 касается зеркала в момент  t₀  + Δt,  и окружностью радиуса  λ₁  с центром в точке Е. Эта касательная линия касается окружности в точке К.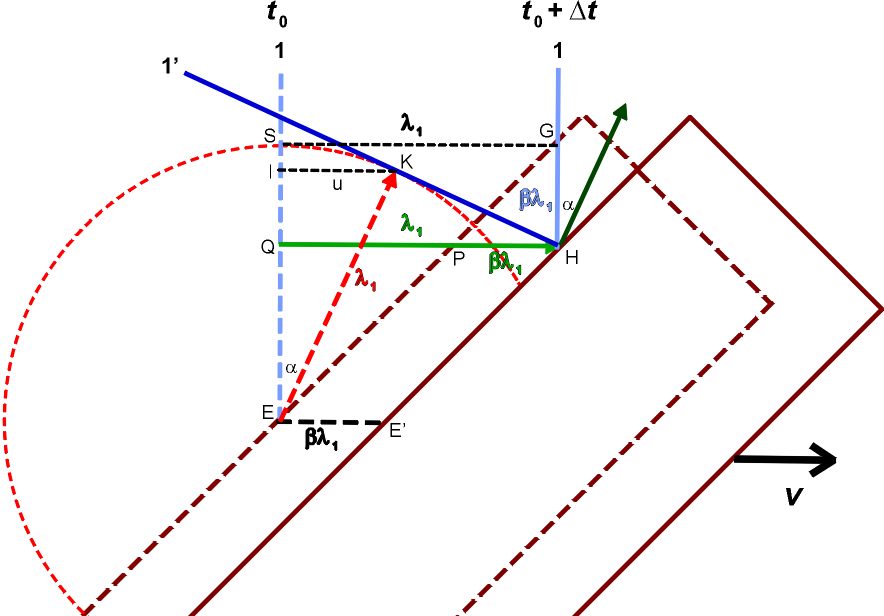
 

 
Чтобы найти угол аберрации отражения  α,  нам надо найти расстояние  |IK|.

sin α = |IK| / |EK|,  а  |EK| = λ₁

Методы решения подобных геометрических задач известны – см., например, здесь (задача 3). Найдем решение нашей задачи, следуя этому примеру.

Пусть начало координат находится в точке Е. Тогда уравнение штрихованной окружности будет

x² + y² = λ₁²

Уравнение касательной будем искать в виде

y = kx + s

Эта прямая проходит через точку H с координатами  H(p, q). Легко увидеть, что  

p = λ₁        
q = (1 – β) λ₁

Это очевидно для оси абсцисс:  |QH| = |SG| = λ₁.  Что касается оси ординат, то поскольку зеркало  а  расположено под углом 45 градусов,  то

|HG| = |PH| = |EE’| = λ₁ β

А координаты точки G:  G(λ₁,  λ₁).

Но мы пока будем искать решение в общем виде, не подставляя значения  p и q.

Точка Н принадлежит касательной, поэтому подставив p и q вместо  х и у  в уравнение  y = kx + s,  мы получим

s = q – kp

Из системы уравнений

y = kx + q – kp
x² + y² = λ₁²

определим общие точки прямой и окружности, для чего  y  из первого уравнения подставим во второе:

x² + (kx + q – kp)² = λ₁²

Возводя в квадрат слагаемые последнего уравнения и приводя подобные члены, имеем:

x² (1 + k²) + x 2k (q – kp) + (q – kp)² – λ₁² = 0

В канонической форме это квадратичное уравнение записывается как

a x² + b x + c = 0

Так как прямая касается окружности (а не пересекает ее в двух точках), данное уравнение имеет единственное решение. Следовательно, его дискриминант   b² – 4ac   равен нулю, то есть:

(2k (q – kp))² – 4 (1 + k²) ((q – kp)² – λ₁²) = 0

Раскрыв скобки и сократив ряд членов, получим

k² (p² – λ₁²) – 2qpk + q² – λ₁² = 0

А сейчас пора вспомнить, что  p = λ₁.  Тогда  p² – λ₁² = 0  и мы получим

k = (q² – λ₁²) / 2qp = ((1 – β)² – 1) / 2(1 – β)

s = λ₁ ((1 – β)² + 1) / 2(1 – β)

Нам нужны координаты точки К(u, w), в которой касательная (отраженный фронт) касается окружности радиуса  λ₁.  Для этого, вернемся к уравнению

x² (1 + k²) + x 2k (q – kp) + (q – kp)² – λ₁² = 0

и подставим  u  вместо  х:

u² (1 + k²) + u 2k (q – kp) + (q – kp)² – λ₁² = 0

Поскольку, как говорилось выше, в точке  К(u, w) дискриминант равен нулю, мы имеем единственное решение

u = – b / 2a = – 2k (q – kp) / (2(1 + k²)) = λ₁ (1 – (1 – β)²) / (1 + (1 – β)²)

Соответственно, поскольку  sin α = u / λ₁,  мы и получим

sin α = (1 – (1 – β)²) / (1 + (1 – β)²)

Ну а  cos α  находится просто решением уравнения

cos α = (1 – sin² α)^½ = 2 (1 – β) / (1 + (1 – β)²)

Уф. Я предупреждал, что вывод громоздкий, хотя ничего особо сложного в нем нет.

UPDATE. Забыл сказать, что Майкельсон и Морли (а за ними все физики, не только релятивисты) без всякого вывода и обсуждения полагают, что

sin α = β

Для малых  β ≪ 1,  это приближенно, вроде бы, так и есть:

sin α = (1 – (1 – β)²) / (1 + (1 – β)²) ≈ β + β²/2 ≈ β

Приближенно. Но мы видим, что Майкельсон и Морли здесь пренебрегают (точнее говоря, не пренебрегают, а не догадываются) эффектами второго порядка  (β²),  относящимися к длине пути и фазе «поперечного» луча  aba₁.  Напомню, однако, что в этом эксперименте как раз и измеряются эффекты второго порядка, то есть те самые  β².