50 лет на Луне. Факты.Техника. Юбилей
448,976 2,686
 

  перегрев ( Слушатель )
05 фев 2018 20:52:16

И снова про старину Пирсона и его коэффициенты

новая дискуссия Дискуссия  404

Я тырнет просматриваю последнее время фрагментарно, ибо капец по работе, а "Циолковский никому не обещал, что космос покорять будет легко" © Веселый, но тут мне личку ломанулся цинично изнасилованный Пирсоном и безжалостно распнутый на зенитном прожекторе крендель с ником, звучание, которого при произнесении вслух, вызывает навязчивую  ассоциацию с принудительно введённым в нескромное место милицейским свистком... Со ссылкой на очередную опровергательскую бредятину от гражданина pmg (perfect 
moon guy) Веселый Простите мне мой английский, но почему нет? Улыбающийся Я к чему, у нашего "лунного парня", что-то там было про корреляции...

Благородные доны, киньте ссылку на табличку, по которой, этот придурок считал коэффициенты корреляции.  Желание самоубиться в очередном лобовом столкновении с учебником, безусловно следует уважать. Улыбающийся
 
  • +0.52 / 13
  • АУ
ОТВЕТЫ (15)
 
 
  Technik ( Слушатель )
05 фев 2018 22:20:56


Всячески приветствуемое желание монсиньора Перегрева ускорить процесс самоубиения главпавиана соседнего зверинца подвигло и меня на некую компиляцию, вреде бы ранее не отмеченную на ветке (за исключением одной ссылки). Нет, конечно, это не Пирсон и не мои друзья Стокс с Рейнольдсом - но и мы... эта... в лаптях по паркету тоже чегой-то исполним.

Представляю семь Apollo 11, 12, 13, ... 17 Image Library - "медиатек", представленных на сайте НАСА. Возможно, кто-то найдет здесь для себя что-то разумное, доброе и вечное (с). На момент выкладки все ссылки рабочие - лично проверял.

https://www.hq.nasa.gov/alsj/a11/images11.html

https://www.hq.nasa.gov/alsj/a12/images12.html

https://www.hq.nasa.…ges13.html

https://www.hq.nasa.…ges14.html

https://www.hq.nasa.…ges15.html

https://www.hq.nasa.…ges16.html

https://www.hq.nasa.gov/alsj/a17/images17.html 

UPD. Перепроверил и подправил ссылки. Теперь запускаются пряма из текста.
  • +0.64 / 11
  • АУ
 
 
  Technik ( Слушатель )
06 фев 2018 10:38:43

- поскольку использованная оценочная характеристика вызвала некоторую реакцию в одном из обитателей оного, должен заметить оному обитателю, что персонально вам до главпавиана расти и расти. Не надо примазываться к чужим достижениям. Оставайтесь тем, кем вы есть - просто п... 
  • +0.34 / 10
  • АУ
 
 
 
  bvlad ( Слушатель )
06 фев 2018 10:43:12

когда,  в каком столетии, увидим булыжник на столе ГЕОХИ  РАН, уважаемый?
  • +0.01 / 10
  • АУ
 
 
 
 
  Technik ( Слушатель )
06 фев 2018 11:22:45

Даже если бы я смог это сделать, я бы этого делать не стал. Ваше стадо вслед за вами тут же заявило бы, что это снято в 3D - ну так на хрена мне париться?

Как вы, опровергуны, предсказуемы - но и талантливы в своем опровержизме... Стоило мне некоторое время назад заявить, что если даже опровергуна vulgaris привезти на Луну и поставить перед посадочным модулем - так сразу же последует вопль, что это макет, и что его накануне доставили туда сверхсекретным американо-китайско-гондурасским космолетом... 

И вот даже моя фантазия превзойдена -
 
"Даже если завтра Илон МАСК снимет 3D, и будет впаривать нам, как  место посадки Аполлон 17 - мы уже знаем в какой пеший поход его послать". 

Молодца, милейший!

Поэтому идите-ка вы ровно в тот же самый пеший поход с вашим булыжником и не возвращайтесь. По крайней мере, сюда, в ветку разумных людей - в зверинце у вас есть шанс повысить свою квалификацию до глав-п..., здесь точно не обломится.
  • +0.66 / 15
  • АУ
 
 
 
 
 
  bvlad ( Слушатель )
06 фев 2018 11:33:05

Маск не может в Луну, это факт! 
А вы не можете  нам булыжник  привезти.  Скучные вы, как и весь ваш юбилей 
  • -0.19 / 8
  • АУ
 
 
 
 
 
 
  Пикейный жилет ( Слушатель )
06 фев 2018 12:00:00

Да. Для вас здесь скучно.
Прощайте.
  • +0.45 / 10
  • АУ
 
 
 
 
 
  Gremlin ( Слушатель )
10 фев 2018 10:35:13
Сообщение удалено
Senya
10 фев 2018 11:21:09
Отредактировано: Senya - 10 фев 2018 11:21:09

  • +0.02
 
 
  Пикейный жилет ( Слушатель )
06 фев 2018 12:31:16

Спасибо. Занес в Архив на первой странице.
Обновляется постоянно всем интересным, что возникает на двух ветках.
  • +0.29 / 7
  • АУ
 
  BomBarDir ( Слушатель )
05 фев 2018 22:51:37

Это одна табличка, из этого оригинала

Это сам экзерсис с бубном  к нему. Веселый
Это второй экзерсис...с выходом  источник где то тут
  • +0.30 / 5
  • АУ
 
  normalized_ ( Слушатель )
06 фев 2018 19:05:54

Бомбардир, дал исчерпывающе вводную.
Там клиент по Пирсону доказывал "корреляции" по минсоставу   "материки" -"моря".
Потом Олег  указал ему  Вчера в 04:55 , что Луна-20 это материк, а не море, как считал до этого pmg натягивая очередную сову на глобус с помощью "Пирсона". (Сове при этом на глобусе было комфортно в обоих случаях).
Дальше pmg начал чесать репу "Бум думать",
Вообще-то то как он пользует (а точнее насилует) Пирсона это пипец на уровне 1-го курса по специальности статистка.
Других слов нет, и смех и грех. Впрочем я особо и не удивился, про корреляцию он давно чушь нес.
https://glav.su/foru…age4067064
А сегодня (прочитав наконец-то за N лет опровергательства ссылку на работы по грунту, и написав что-то типа "да, их оказывается много")  написал, что придумал новый метод, но ему нужно еще данные.
Если Вы хотите ему объяснить про корреляцию, то конечно можно, ибо даже по старому его способу там же "ужас".
Я бы на его месте не изобретал бы велосипед как научный фрик (в теме в чем он посредственно разбирается), а просто ознакомился бы по теме статистики вообще (зачем она, когда применяют Пирсона и главное зачем), как сравнивают по признакам и зачем, по теме кластеризации и представлению признаков, по анализу выбросов, как проверяют гипотезы и по каким критериям в каких случаях, наконец как данные делают normalized и зачем.
Потому что то, что там "придумал" с Пирсоном это издевательство, которое сойдет, ну, может в физкультурном институте когда преподавателей заставляют рассчитывать статистику (для галочки, естественно), но уже никак не в т.н. "физкультурном техникуме" (физтехе) на котором он вроде бы учился.
  • +0.15 / 14
  • АУ
 
 
  BomBarDir ( Слушатель )
07 фев 2018 16:17:57

Прикол в том, что корреляционный анализ, насколько мне позволяет вспомнить мой склероз, это метод (или инструмент, не помню уж) позволяющий установить статистическую зависимость между какой то там выборкой, заранее подготовленной по определённому правилу. В результате построения корреляционного поля можно оценить зависимость. Она или есть (сильная или большая штоле?) или её нет. Всё.
pmg, как любой опровергаст, прикручивает к, прости хоспади, ращёту заранее сформулированный тезис представляя его как вывод из ращёта, который он, якобы, в поте лица намастырил. Похожей методой пользуется электросекс Коновалов, который долго и нудно рассказывает как бы он снял ту или иную сцену (попёртую, кста, с фотографий НАСА, а не плод его креатива,) а в конце объявляет, что на основании его постановки, все фотки сняты в павильоне. Бггг...
  • +0.23 / 10
  • АУ
 
 
 
  normalized_ ( Слушатель )
09 фев 2018 11:44:02

Пирсон если "1" или "-1" то сильная корреляция (или отрицательная корреляция, тоже связь), а именно мера линейной зависимости. Если 0, то корреляции нет.

Но нужно учитывать, что из корреляции не обязательно  следует причинно-следственная связь (а вот где есть связь, там часто обнаруживается корреляция). То есть существуют так называемые ложные корреляции.
В учебниках часто дают веселые примеры:

а) случайные совпадения
Например данные о количестве людей, утонувших в бассейне и количеством фильмов, в которых снялся Николас Кейдж.
Или 

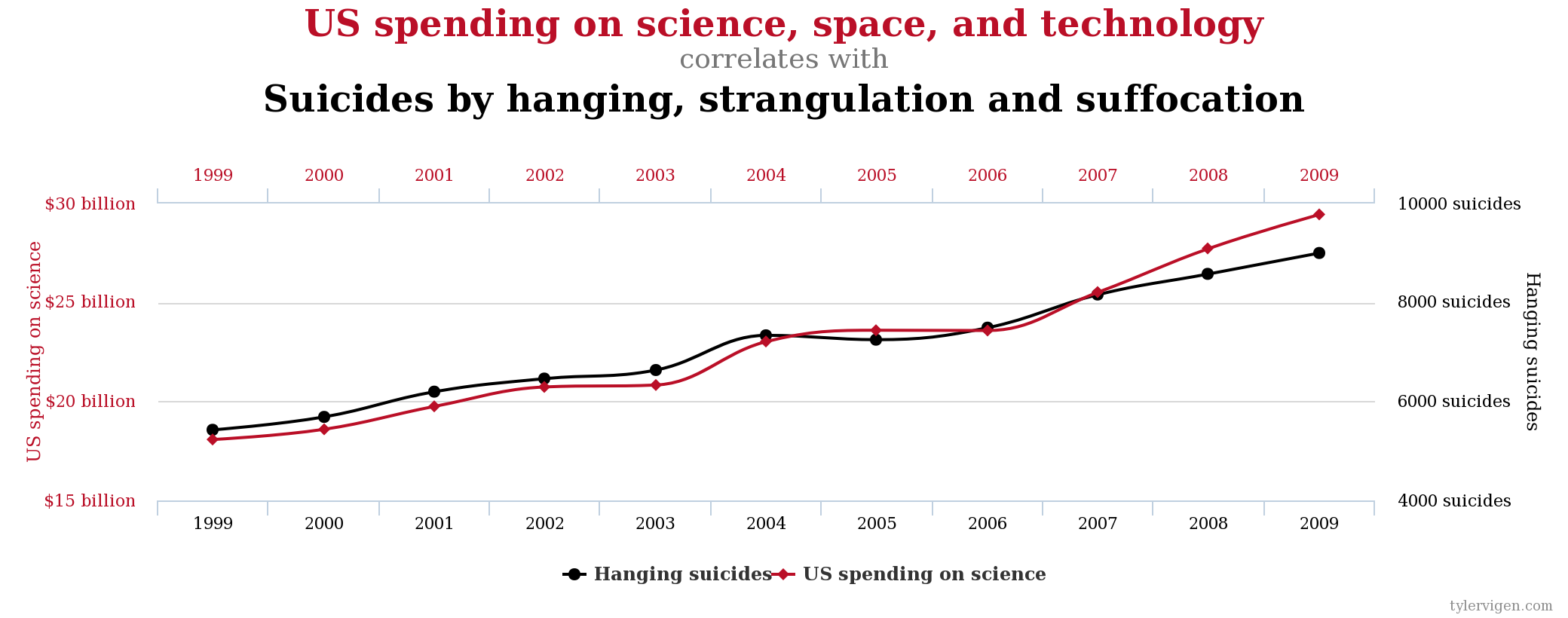
Затраты США на науку, космос и технологии / Суициды путем повешения и удушения. Корреляция 99,79%.




Доля разводов в штате Мэн / Среднее потребление маргарина. Корреляция 99,26%




Тут еще "Безумные корреляции":
http://rationalnumbe…rrelyacii/


б) Есть корреляции объясняющихся воздействием третьего скрытого признака.

Например, количество самоубийств и кол-во радиоприемников на душу населения сильно положительно коррелировано (воздействие скрытой связи "размер города")

Или есть корреляция: чем больше продается мороженного на пляже, тем больше утопленников.
корреляция (на каком то пляжу где записывали данные) слабая 0,33, но имеется. 



Можно, конечно, сразу делать вывод опровергательстких масштабов: то ли чем больше едят мороженного, тем чаще тонут от переизбытка сладости, то ли раз чаще тонут, то другие больше едят мороженное на нервной почве наблюдая праздно за шумихой. Но на самом деле есть скрытая третья переменная, через которою есть связь (температура) 

Кроме этого нужно избегать других неточностей.

1. Во первых, автор сравнивает коэффициенты корреляции (как меру похожести) по отношению только к одним опорным данным (выборкой это назвать сложно, но об этом ниже ) — по Луне-16 —  а не сравнивает миссии попарно.

Это аналогично тому, что при сравнении "близости" разных точек  О, A и B на плоскости, сравниваются только их расстояния до одной точки О. 
Чисто геометрически, даже если "расстояния"  ("похожести") до основной точки будут одинаковые (т.е. расстояние OA примерно равно OB), ничего нельзя сказать о похожести AB (они могут быть как далеко друг от друга, на противоположенных сторонах окружности вокруг О, так и рядом).


2. Как указано по ссылке (данной Выше) автор не совсем понимает,  что такое корреляция и почему, например, коэффициент корреляции между измерениями:

одного ученого: 1, 2, 3
и другого: 50, 80, 150.

будет вообще аж 0.974! Но это не означает равенства (и верности, и схожести) измерений между этими данными.

Корреляция лишь отражает линейную зависимость (и возможную связь), а не равенство.


3. Не делают корреляцию вдоль разнородных данных  (процентовок  разных оксидов, слонов и попугаев).

Коррелируют или выборки, 
а) скажем берут 10 миссий, смотрят  для них корреляцию оксида Магния (10 значений) или Марганца (10 значений). Для установки зависимости между одним элементом или другим .

б) Или делают сравнение или проверку гипотез ставя те или иные вопросы.
Например, берут выборки 5 миссий (марганца) и 10 миссий (тоже марганца) и отвечают на вопрос (проверяют гипотезу) равны ли средние выборок (или же просто случайно отличаются). Для этого применяют критерии. Причем если известно распределение и его параметры то параметрические, если нет, то непараметрические критерии. И там тоже есть всякие нюансы.

(об этом ниже)

4. Дальше, если просто смотреть на цифры (понимая по предыдущему пункту, что нельзя сравнивать разнородные признаки корреляцией вдоль них), то можно заметить, что минералы со концентрациями близким к 0% практически не участвую в оценке коэффициента корреляции. (Оксиды марганца, калия, натрия)

На графике они около точки 0 и наложились друг она друга.




Они могут отличаться хоть в 10 раз (между миссиями) но сильно  от этой нулевой точки не уйдут. Прямая это не "почувствует". Их изменение не влияет на вычисленный коэффициент Пирсона. Меняй хоть в 10 раз оксиды натрия или марганеца. Пирсон покажет, что образцы практически так же "похожи"

Можно это заметить, что если убрать эти оксиды из данных, то останутся точки которые сильнее разбросаны от прямой. За счет сокращения базы среднего, коэффициент уменьшится.




И наоборот, если добавить оксиды "серебра" золота" (нулевые точки причем хоть одинаковые, хоть отличающиеся в 10 раз, но они при этом все равно малые, около нуля), то КП увеличится (кол-во точек будут уменьшать среднее "отличий")






6) Чтоб обрабатывать задачу желательно

- сделать визуальное представление данных о чем речь (обзор)
- похожесть сравнивать попарно
- нормировать данные (при вычислении похожести)
- для сравнения попарно нужно выбрать измерение "похожести". Коэффициент корреляции не единственный, можно  применять другие метрики "расстоянии" (например cosine или евклидово)
- попробовать представить на плоскости (понижение пространства) чтоб посмотреть, кто более с кем похож визуально,  кластеры и  выбросы. 
- проверять те или иные гипотезы по тем или иным признакам.

В качестве примера. (И для небольшой разминки)

Воспользовавшись исходными данными автора из 05 февраля 2018,

i
mission
type
SiO2
Al2O3
TiO2
FeO
MgO
CaO
Na2O
K2O
MnO
1
Л16
Море
41.70
15.33
3.39
16.64
8.78
12.49
0.34
0.10
0.21
2
Л20
Горы
44.20
22.90
0.56
7.03
9.70
15.20
0.55
0.10
0.12
3
Л24
Море
43.30
15.20
1.13
16.30
8.69
13.10
0.42
0.04
0.22
4
A11
Море
41.90
13.55
7.56
15.94
7.82
12.08
0.40
0.13
0.21
5
A12
Море
45.90
12.50
2.81
16.40
10.00
10.40
0.41
0.25
0.22
6
A14
Горы
47.20
17.20
1.79
10.40
9.37
11.00
0.66
0.58
0.14
7
A15
Море
47.07
14.17
1.75
14.92
10.44
8.95
0.39
0.20
0.18
8
A16
Горы
45.17
26.71
0.59
5.57
6.03
15.61
0.44
0.12
0.08
9
A17
Море
40.37
11.60
8.99
17.01
9.79
10.98
0.32
0.08
0.23



Понятно, что сами исходные данные агрегированы (то есть уже усреднены)  и нтересней было бы иметь больше данных, чтоб делать открытия (не в кавычках).
Тем не менее для небольшого урока и разминки:

Общая картина



Разбивка по типу (Суша или море)



Так как оксиды с низким  содержанием плохо видны, то отобразим их отдельно


Черный отрезок визуализирует средне квадратичное отклонение.
Справа Violin_plot аналог Бокс-Плота (ящики с усами) только с KDE

Так как автор пытался осмыслить корреляцию концентраций, посмотрим их попарное соотношение визуально.

(Примечание: делать выборку разнородных величин, как указано выше, не верно, но посмотреть можно)





Столбцы и строки на графике соответствую миссиям.
В ячейках правого верхнего угла нарисовано распределение оксидов соответствующей пары миссий
В нижнем левом углу тоже самое с вычисленными коэффициентами Пирсона, и вычисленная линейная регрессия (не имеет к Пирсону прямого отношения, например она не обязательно проходит через точку 0).

Отдельно по морям



Отдельно по материкам



Корреляционная матрица

На попарных графиках выше мы посмотрели на данные, но они в данном случае разбросаны и не информативны (а вот в реальных задачах с выборками уже могут появиться идеи и наблюдения как обрабатывать дальше), за деревьями леса не видно.
Поэтому отдельно посмотрим на корреляционную матрицу.

Опять же примечание: что "выборка" по разнородным данным, но мы тут исправляем "недочет" автора не использующего попарное сравнение коэффициента корреляции.



В цифрах: mc_corr_pearson_all.csv (Собственно, автор смотрел только на одну строку из этой матрицы)


Матрица симметричная (относительно диагонали) и цвет ячеек соответствует коэффициентам корреляции между миссиями. 
Чем темнее ячейки, тем больше коэфф. Пирсона между соответствующими парами.
(опять замечание, что между разнородными кучами попугаев и ежей) 

Тем не менее тут уже кое что можно заметить.
Например, Луна-20 больше всего "совпадает" с Аполлон-16.
Все они сильно "коррелируют" (левая картинка темная), самые непохожие пары имеют коэффициент 0,861

К слову, кроме Пирсона можно использовать и ранговые корреляции (они меньше чувствительны к выбросам) Спирмена и Кендела
Соответствующие корреляционные матрицы






Теперь отобразим отдельно Горы и Моря 
(можно было бы сгруппировать  автоматически по данным матрицам, то есть кластеризовать, с тем или иным параметром число групп)





Внутри каждой из этих групп пары коррелируют сильнее, нет пар с коэффициентом корреляции меньше 0,9773 и 0,9603 соответственно, тогда как на общей корр. матрице минимум 0,8681.
Визуально это заметно тем, что на левой части практически нет таких светлых ячеек как на общей матрице.

Это собственно то, что должен был корректно продемонстрировать автор по своему методу (исправлена ошибка не попарного сравнения).

Проверка гипотез.

(в качестве примера, что можно сравнивать однородные данные) вернемся к графику:




Видно, что для некоторых оксидов есть подозрение на статистическое отличие между материками и морями
Проверим это формально на примере SiO2.
Содержание SiO2
В морях: 41.7 ,  43.3 ,  41.9 ,  45.9 ,  47.07,  40.37
На суше: 44.2 ,  47.2 ,  45.17

Можно было бы применить критерий Стьдента для проверки гипотезы значимого отличия средник, но перед этим мы должны проверить, а нормальное ли распределение.
Для этого сначала визуально проверим вероятностные графики, а потом применим критерий Шапиро-Уилка.




На прямой точки лежат не близко, уже подозрения.

Критерий Шапиро-Уилка
  • H0: Кол-во SiO2 (в выборках суша и море) распределены нормально

  • H1: не нормально.


Задаем уровень значимости alpha 0.05 (95.0% уровень доверия)
Проверка Shapiro-Wilk 'Море': W-statistic: 0.92456138134, p-value: 0.538803696632
Отвергаем гипотезу H0

Тоже самое для Гор:
Проверка Shapiro-Wilk 'Море': W-statistic: 0.92456138134, p-value: 0.538803696632
Отвергаем гипотезу H0

Гипотезу о нормальности выборок отвергаем, так как p-value большое (больше 0.05)
Критерий Стьюдента применить нельзя.

Поэтому применяем непараметрический критерии [ например U-критерий Манна — Уитни]

MannwhitneyuResult(statistic=4.0, pvalue=0.1226390584033864)

pvalue больше уровня значимости
Гипотезу о том, что выборки (SiO2 для гор и морей) не отличаются, отвергнуть нельзя.

Теперь тоже самое на примере оксида алюминия Al2O3.



Критерий Шапиро-Уилка. Гипотезы
  • H0: Уровень Al2O3 (в выборках суша и море) распределены нормально

  • H1: не нормально.


Задаем уровень значимости alpha 0.05 (95.0% уровень доверия)

Проверка Shapiro-Wilk 'Море': W-statistic: 0.937569320202, p-value: 0.639681518078
Отвергаем гипотезу H0
Проверка Shapiro-Wilk 'Море': W-statistic: 0.937569320202, p-value: 0.639681518078
Отвергаем гипотезу H0

Так как p-value большое (больше 0.05) отвергаем гипотезу о нормальности.
Критерий Стьюдента применить нельзя.

Поэтому применяем непараметрический критерии [U-критерий Манна — Уитни]
MannwhitneyuResult(statistic=0.0, pvalue=0.014092901073953692)

Гипотеза о том, что выборки не отличаются можно отвергнуть в пользу гипотезы что средние концентрации Al2O3 отличаются.

Это можно заметить (подозревать) и визуально и на выше приведенном графике.

Замечание:
При больших объемах, например когда проверяют гипотезы и сравнивают влияние генов и очень большого ко-во гипотез, то проводят множественную проверку.
Например, если тестировать отличия по большому объему данных и очень много гипотез, то рано или поздно возможно случайное отклонения измерений.

Один из примеров (другие по ссылке). Американский психолог и парапсихолог Джозеф Райн, который занимался исследованиями экстрасенсорных возможностей разных людей,  проводил следующие эксперименты. На первом этапе он делал предварительный отбор.
Испытуемому давали 10 карт, и он должен был угадать их цвета.
Оказалось, что два человека все 10 карт угадали, еще девять человек угадали 9 из 10 карт.
Но по этим данным нельзя делать выводы, что экстрасенсорные способности проявились, так как число испытаний было большим 1000 человек.
Из такого кол-ва рано или поздно кто-то из людей угадает случайно.

После того как Джозеф Райн отобрал этих людей, угадавших цвета карт, как экстрасенсов, он предложил им еще раз пройти этот эксперимент . Ни один не подтвердил свои способности.
Отсюда  Джозеф Райн сделал вывод, что если человека объявить экстрасенсом, то его способности сразу пропадают.

Можно посмотреть на график вероятности, что хотя бы один угадает цвета 9 из 10 карт в зависимости от количества испытуемых

Видно, что вероятность растет быстро, уже при 100 испытуемых вероятность  найти одного экстрасенса больше 0,5, а при больших количествах испытуемых вплотную приближается к 1, очень вероятно что кто-то угадает.

Для нивелирования эффекта множественности и вероятности ошибки "хорошего промаха" (ошибки первого рода), при проверке множественных гипотез можно уменьшать уровень значимости 0.05 пропорционально кол-ву в группе (Поправка Бонферрони), но есть и другие методы.
Вот такое короткое замечание...

Понижения размерности

Для кластеризации данных мало, но можно посмотреть как соотносится состав грунта от миссии к миссии.
Формально будем считать, что у каждой миссии есть несколько признаков (в данном случае вещественных) как концентрации 9 оксидов.
Представим эти 9 признаков в пространстве размерности 2 (для визуализации на плоскости).

В первою очередь проведем нормализацию данных (т.е. отмасштабируем или стандартизируем) мелкие концентрации повысим, и выравним масштаб и смещение, чтоб все были с одинаковым СКО).

Для начала используем ранговый метод tSNE


На этапе визуализации подсветим сушу и море разными цветами.
(Этот график не единственное точное отображения, так как определяется случайностью)
Ничего тут особо не скажешь, Луны разбросаны и Аполлоны тоже.

Теперь MDS.

Для него в качестве вспомогательной метрики (отличие между признаками) можно использовать "расстояния".
Вот одним из вариантов этой метрики и может выступать матрица корреляции (но уже по стандартизированным данным вдоль миссий )



Для больших данных часто применяют cosine расстояния между признаками, или евклидово:








Вот по всем этим метрикам можно заметить зачатки двух кластеров: моря и суши. (А то и три)
Но как писалось выше, когда мало данных, то не очень интересно. Можно было бы делать и другие картины, считать (обнаруживать), ставить вопросы и их делать оценки, есть ли выбросы, которые могут быть примечательными особенностями, естественные, интересные или обнаружить открытия.

Выводы


Рекомендация автору: чем изобретать велосипед применяя чистый разум (т.е. не отягощенный знаниями) и путаться в трех соснах в бесплодных попытках опровергать полеты не вставая в дивана,  сначала полезней ознакомиться с тем, что давно до него изобрели умные люди, и вообще со статистикой.

http://baguzin.ru/wp…chnye-kri/ (всю книгу)
Или по профилю:
Биостатистика и язык R: Понижение размерности: PCA, MDS, t-SNE



 


У меня сложились очень похожие впечатления.
  • +0.87 / 17
  • АУ
 
 
 
 
  BomBarDir ( Слушатель )
09 фев 2018 13:48:24


Камрад, снимаю шляпу. Вернулся во времена своей юности и испытал давно забытое ощущение невероятного облегчения от того, что наконец то отмучил 2 пары и семинар по матстату. И можно с друзьями и подругами, с чистой совестью, завалиться в кафешку "Лакомка" и под пироженные "Картошка" с "Портвейном" (взятым, есессно по пути в ""Лакомку") впасть в полное забытиё перед завтрашней парой лекций по ненавистному матстату.

Жаль только одного, опровергасты даже читать не станут. У них уже есть готовый вывод, так что некуй читать многАбукав.

Уволоку к себе такую полезняшку. А вы говорите опровергасты никакой пользы не приносят! Ты посмотри какого Пегаса тебе прислал pmg. Без него ты бы сроду ничего подобного бы не родил. Смеющийся

ЦитатаУ меня сложились очень похожие впечатления.


Это, друг мой, не впечатление...Это осязаемая реальность. Веселый[/quote]
  • +0.45 / 8
  • АУ
 
 
 
 
 
  normalized_ ( Слушатель )
09 фев 2018 15:14:22


Спасибо, что читаете.

Ну я как раз  больше  для себя (в качестве упражнения) и для нормальных писал, чем для него.
К сожалению Перегрев в запарке, а то бы и он еще больше приложил. И веселее.
А так не трудно, сейчас библиотеки есть и по визуализации и по расчетам. И все это известно. Там самое сложное, что нужно иметь представление, что бывают такие-то понятия, и держать в голове, что нужно не забыть проверить это и это.

Просто при чтении разбираемого автора у меня волосы на голове встали, куда он лезет? Я еще понимаю, чудак который вообще ничего не знает (и не хочет знать) про космические полеты и как их делают и испытывают технику, но разбираемый автор же институт кончил вроде неплохой, пусть и "упался" на опровергательтсве. Если ему просто написать "у тебя тут ошибка, вот", то он это все равно же пропустит мимо ушей  из-за тенденция селективного восприятия. И даже не поймет насколько глубоко ошибается ("подумаешь, ошибка, первый раз что ли? При опровержении полетов это дело житейское, обычное и ежедневное, в главном то все равно прав. главное то отряхнуться как ни в чем не бывало, и опровергать дальше", подумает он. Забудет все равно, и опять вылезет через неделю с тем же самым или подобным бредом.

А вообще статистика (и не только) дело интересное, но там не просто прикол, что графики нарисовать (это просто "пощупать" данные с разных сторон, с чего начать их изучать) или бездумно  что-то посчитать, среднее или показать "рост". Там самое интересное, что нужно ответить на некоторый вопрос (не все вопросы), например  стоит ли принимать такое то решение или не стоит.
Причем ответить на него нужно объективно, воспроизводимо, точно, обосновано, а не кулуарно, и в тоже время не случайно, как бог на душу положит или по своим личным предпочтениям (Хотя и есть правда, что статистику можно натягивать на глобус, и в некоторых вопросах должна быть этика, вот поэтому ее тоже нужно знать)
Собственно поэтому  это "оружие" более ста лет назад и не давали публиковать тому самому "студенту". Ибо для производителя пива Гинесс критерии принятия решений в селекции ячменя считалось коммерческой тайной, о которой не должны были знать конкуренты.
Сейчас, конечно, решения не только на основе критериев должны применяться (смотря какие), но в простейших вещах не должно быть ошибок в обоснованиях.
  • +0.69 / 14
  • АУ
 
  Пикейный жилет ( Слушатель )
12 фев 2018 01:20:10

perfect moon guy - истинный лунный парень

По моему отличный перевод.
Варианты перевода , (guy- выставлять на посмешище, издеваться, насмехаться, пугало, чучело) 
мы c негодованием отметаем.
Только perfect- полный, чистый, совершенный.
Гип Гип Ура !!! Не могу на него не нарадоваться.
  • -0.01 / 6
  • АУ
 
<< .
Сирийско-российский Бизнес-Форум >>