Тред №315983

новая дискуссия Дискуссия  556

Эти совершенно тривиальные рассуждения имеют самое прямое отношение к волновому уравнению (и вообще ко всем дифференциальным уравнениям физики), как вы вскоре убедитесь. Сейчас же мы рассмотрим волновое уравнение несколько другого вида (оно используется в школьных учебниках и в университетских учебниках для нефизиков), которое описывает распространение фронта волны:

x^₂ + y^₂ + z^₂ = c^₂t^₂

Это уравнение, возможно, не столь «научно», как волновое уравнение в частных производных:

∂^₂u/∂t^₂ – c^₂∇^₂u = K(x, y, z, t)

Но оно имеет то преимущество, что оно очень наглядно. Будем его использовать как «нулевое приближение», как «контроль на физический смысл», для качественной оценки волновых процессов. С ним труднее сделать ошибки.

Легко увидеть, что уравнение  x^₂ + y^₂ + z^₂ = c^₂t^₂  описывает распространение фронта сферической волны, которая была испущена из точки с координатами  (0, 0, 0)  в момент времени  t = 0.  Чем больше  t,  тем больше сфера с радиусом   r = (x^₂ + y^₂ + z^₂)^₀.₅ = ct.

Но ведь волны – это не один только импульс в нулевой момент времени, правильно? А как нам описать распространение волны, испущенной в момент  t_₁? А мы только что разбирали похожий пример – как:

x^₂ + y^₂ + z^₂ = c^₂(t – t_₁)^₂

Подчеркнем, что это – другая волна, другая единичная функция, если мы пользуемся только четырехмерным пространством  (x, y, z, t).

Теперь предположим, что источник движется с произвольной скоростью  v  в произвольном направлении и излучает волны, одну за другой. Как мы можем описать это семейство волн? Распространение каждой волны, испущенной в точке с координатами  (ξ, η, ζ)  в момент времени  ԏ, будет удовлетворять следующему уравнению:

(x – ξ)^₂ + (y – η)^₂ + (z – ζ)^₂ = c^₂(t – ԏ)^₂

или

r – r_и = c(t – ԏ),

где  r – это радиус-вектор (из начала координат) какой-либо точки распространяющейся волны в момент  t,  r_и – радиус-вектор источника волн в момент  ԏ.

Подчеркнем, что в четырехмерном пространстве  (x, y, z, t)  это не одна, а много единичных волн, каждая со своим центром излучения  (ξ_c, η_c, ζ_c)  и моментом излучения  ԏ_c. Обратите внимание, что  r, r_и и ԏ  (или  ԏ_c)  здесь имеют совсем другой смысл, чем в определении запаздывающих потенциалов. Отметим также, что  r_и  и  ξ, η, ζ  являются переменными, зависимыми от  ԏ: 

r_и = r_и(ԏ),  ξ = ξ(ԏ),  η = η(ԏ),  ζ = ζ(ԏ).

В интернете есть много физических апплетов, в том числе для эффекта Доплера. См. например,

http://www.astro.ubc…ppler.html
http://www.lon-capa.…pler/d.htm

Эти апплеты как раз и показывают распространение волн от источника, движущегося с постоянной скоростью. Ниже показан мгновенный снимок (Print Screen) последовательных волн, распространяющихся от источника со скоростью  v = 0.707 c:
 

 
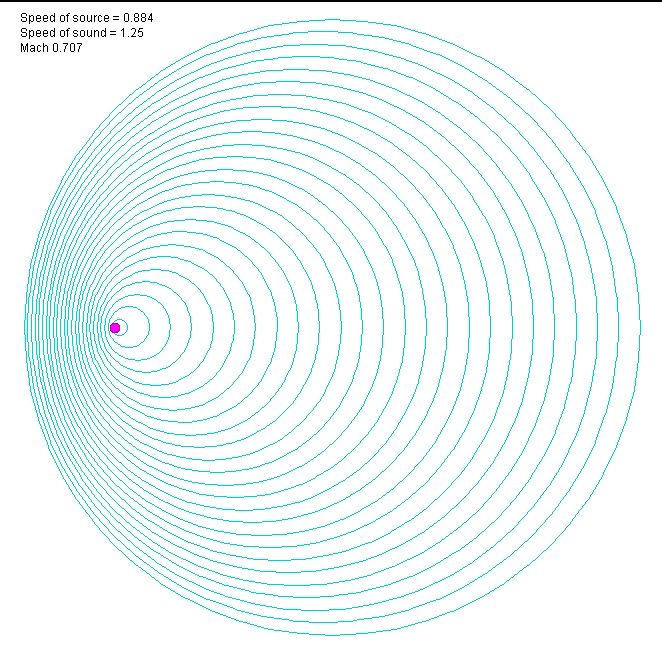
Сравнивая уравнение  (x – ξ)^₂ + (y – η)^₂ + (z – ζ)^₂ = c^₂(t – ԏ)^₂  с тем, что написано выше о полной функции  y = 3(x – u)^₃ + p  в четырехмерном пространстве, легко понять, что любая полная функция  f, описывающая распространение всех волн от движущегося источника, должна зависеть не только от переменных  x, y, z  и  t,  но и от  ξ, η, ζ  и  ԏ. То есть она должна зависеть от 6 пространственных и 2 временных координат, а изображаться, соответственно, в 9-мерном пространстве:

f = f(x, y, z, ξ, η, ζ, t, ԏ)

Полный дифференциал этой полной функции будет равен:

Df = (∂f/∂x)dx + (∂f/∂ξ)dξ + (∂f/∂y)dy + (∂f/∂η)dη + (∂f/∂z)dz + (∂f/∂ζ)dζ + (∂f/∂t)dt + (∂f/∂ԏ)dԏ

Поскольку  x и ξ, y и η, z и ζ, t и ԏ  всегда встречаются парами:  f  = f(x - ξ, y - η, z - ζ, t - ԏ), то нетрудно убедиться, что

Df = (∂f/∂x)(dx – dξ) + (∂f/∂y)(dy – dη) + (∂f/∂z)(dz – dζ) + (∂f/∂t)(dt – dԏ)

Если источник движется по прямой линии, то оси координат можно выбрать так, чтобы движение происходило только по оси x, а η и ζ  в любой момент времени были равны нулю. Тогда их можно исключить из рассмотрения и остаются только  x, y, z, ξ, t, ԏ. Если, далее, источник движется с постоянной скоростью  v_₀, мы можем выразить  ξ  через  ԏ:

ξ = v_₀ԏ

Это, однако, не позволит нам избавиться и от  ξ  тоже, поскольку  ξ  остается переменной. Избавиться можно только от тех переменных, которые в любой момент времени равны нулю или константе. Таким образом, минимальное количество пространственных координат для описания источника, движущегося по прямой линии, должно быть 4, а временных координат – 2:

Df(x, y, z, ξ, t, ԏ) = (∂f/∂x)(dx – dξ) + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)(dt – dԏ)

Если же мы не учитываем переменных  ξ  и  ԏ  и считаем, что полный дифференциал равен

df = (∂f/∂x)dx + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)dt,

то это не полный дифференциал от полной функции  f(x, y, z, ξ, t, ԏ)  в семимерном пространстве  (x, y, z, ξ, t, ԏ, f), описывающей все волны от источника, испущенные во все моменты времени, а единичный дифференциал в пятимерном пространстве  (x, y, z, t, f)  только одной единичной волны, испущенной, скажем, в момент  t_₁ в точке  x = x_₁, y = 0, z = 0:

df(x, y, z, x_₁, t, t_₁) = (∂f/∂x)dx + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)dt

Напомню, что эта единичная волна распространяется со скоростью с и в любой момент времени она должна удовлетворять уравнению

(x – x_₁)^₂ + y^₂ + z^₂ = c^₂(t – t_₁)^₂

или

r – ix_₁ = c(t – t_₁),

где  i, j, k – единичные векторы по осям x, y, z.

Во всех точках вне этой расширяющейся сферы, единичная функция  f(x, y, z, x_₁, t, t_₁) равна 0. Обозначим |r – ix_₁|  как  r_₁, а направляющие косинусы луча волны как  cos α, cos β и cos γ. Подчеркнем, что если источник испускает последовательные волны, а не одну-единственную волну, то для любой единичной волны  cos α ≠ (x – x_₁)/r_₁,  cos β ≠ y/r_₁,  cos γ = z/r_₁,  поскольку лучи волн, как будет показано ниже, искривляются. При распространении волны, cos α, cos β и cos γ все время меняются, они не постоянны.

Заметим, что если в момент времени  t  единичная волна находится в точке (x, y, z), то в момент  t + dt  она переместится на расстояние  cdt  от центра волны – точки с координатами (x_₁, 0, 0). При этом, x, y и z изменятся одновременно и пропорционально  cdt:

dx = cdt cos α
dy = cdt cos β
dz = cdt cos γ

• +0.00 / 0