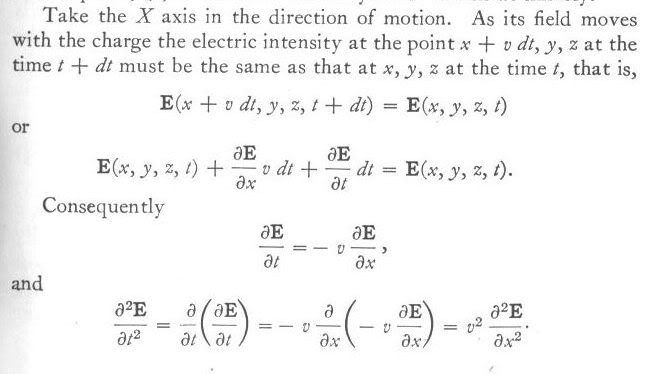Жизнь, Разум, Человек, Религия и Наука
150,330
565

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Я решил создать свою личную ветку, чтобы иметь возможность последовательно изложить свои идеи на эти темы, вместо того, чтобы распыляться на многих ветках. Думаю, читателям так будет намного легче понять мою концепцию.
Ряд лет я работаю над книгой, посвященной этим вопросам. Это не обзор существующих точек зрения, а мои собственные идеи и теории. В конечном итоге, моя книга - это попытка предложить человечеству Новую Парадигму, новое осознание своего места во Вселенной и новые цели развития. Я надеюсь, эта книга поможет России пережить один из самых трудных периодов в ее истории и сформулировать новую Великую Цель.
Я хочу выложить некоторые части этой книги (которая пока что в основном состоит из заметок для памяти) на форуме и обсудить их. Надеюсь, что они будут интересны участникам. Мне же это поможет увидеть недостатки текста, ответить на вопросы, о которых я сам не думал или ответы казались мне слишком очевидными.
По определенным соображениям, я планирую впервые опубликовать ряд моих научных идей в этой книге, а не в рецензируемых научных журналах. Это означает, что они будут обсуждаться сначала (до публикации книги) на данном форуме - открыто для всех. Соответственно, есть вероятность воровства этих идей. Единственным доказательством моего приоритета (и приоритета российской науки) являются дискуссии на этом форуме. Уважаемые посетители форума, все вы свидетели, что впервые прочитали это здесь. В начальный период развития науки, такое выкладывание на всеобщее обозрение было в порядке вещей (многие открытия были «опубликованы» всего лишь в форме писем от одного любителя науки к другому), но сейчас приоритеты устанавливаются публикацией в научных журналах. Я, можно сказать, возвращаюсь к этическим нормам начала науки.
Хотя изначально я такой цели не ставил, в ходе своей научной работы и размышлений я обнаружил множество серьезных ошибок и заблуждений в ряде наук. Мне придется поэтому значительное время посвятить "разоблачению" этих ошибок. Если разобраться, многие из них возникли из-за того, что человек, как правило, видит только то, на что ему сказали обратить внимание. Смотреть и видеть - разные вещи. Видеть реальность, видеть "очевидные", "бросающиеся в глаза" факты - очень трудно. Ярким примером такой особенности человеческой психики является это короткое видео, которое довольно известно (на английском). Для тех, кто английского не знает:
Показаны 8 баскетболистов, 4 в белой форме и 4 - в черной. Диктор спрашивает: "Сколько передач делает команда в белом?" И баскетболисты начинают бросать мячи друг другу. Сколько Вы насчитаете передач?
http://www.youtube.c…hg6qcgoay4
Первопроходцы, создатели науки зачастую определяют все последующее мышление поколений своих последователей, которые видят проблему строго в рамках, заданных отцами-основателями, не могут вырваться из колеи. Я надеюсь показать читателям ряд таких ошибок, ложных догм (и попытаюсь убедить их, что это именно ошибки). Я увидел их далеко не сразу - долгое время, я находился в плену тех же иллюзий, что и все остальные ученые. Уверен, что еще большее число "медведей" я не заметил. Я говорю не о мелких ошибках, неточностях, а о фундаментальных, исправление которых требует пересмотра всей данной науки. Например, почти всей науки о происхождении жизни. Например, почти всей физики.
Я не разрушитель по характеру и не садист, мне не доставляет никакого удовольствия выставлять людей, всю жизнь занимавшихся наукой, идиотами и показывать, что все, что они сделали в науке, ничего не стоит. Тем более что я так не думаю (что они идиоты и что их труд ничего не стоит). Тем не менее, такой может быть реакция общества и, в частности, политиков (когда мои идеи победят): "На что вы деньги народные потратили?" Что касается физики, то ответ простой - посмотрите вокруг себя, все технологии, которыми вы пользуетесь, созданы благодаря открытиям физиков.
На самом деле, большинство физиков должны только радоваться тому, что физика будет пересмотрена. Открывается огромное поле для новых открытий. Те физики, кто первыми успеют "переписать" старые разделы физики по-новому, вообще станут классиками науки - новые формулы будут носить их имена. То же и с происхождением жизни, с поиском и изучением новых форм жизни на Земле, которые я предсказываю. Пострадать, в какой-то степени, могут только крупные чиновники от науки, которые добивались выделения огромных денег на ускорители. Физика же как наука получит новый старт и новые возможности.
Я буду говорить о научных вопросах - или о "ненаучных" с научной точки зрения. Писать я буду как можно более простым языком, чтобы было понятно как можно более широкому кругу читателей. Злоупотреблять наукообразными терминами я не буду. Слишком много обзорной информации и объяснений терминов я, впрочем, давать не смогу - в интернете полно сайтов, где даются такие объяснения (достаточно кликнуть на термине правой кнопкой мыши и выбрать "искать в Google термин"). Но, в общем, представителям естественных наук и технарям (физикам, инженерам, химикам) большинство должно быть понятно.
Насчет копирайта: хотя это будет позднее опубликовано в виде книги (вероятно, со значительными добавлениями и исправлениями), перепечатки и распространение в некоммерческих целях моих статей с данного форума разрешены и приветствуются (с обязательной ссылкой на авторство и первоначальный источник - данный форум). Я больше заинтересован в максимальном эффекте от моего труда, чем в максимальной прибыли от публикации (что не означает, что я разрешаю бесплатные перепечатки в коммерческих целях).
P.S. Что касается ролика - после первого показа бросания мяча, диктор говорит: "Ответ - 13. Но видели ли Вы медведя с лунной походкой?" Повторяется видео и зритель, как правило, только при повторном просмотре, действительно, видит медведя. В конце сообщение: "Легко не заметить что-то, если ты не ищешь этого".
Ряд лет я работаю над книгой, посвященной этим вопросам. Это не обзор существующих точек зрения, а мои собственные идеи и теории. В конечном итоге, моя книга - это попытка предложить человечеству Новую Парадигму, новое осознание своего места во Вселенной и новые цели развития. Я надеюсь, эта книга поможет России пережить один из самых трудных периодов в ее истории и сформулировать новую Великую Цель.
Я хочу выложить некоторые части этой книги (которая пока что в основном состоит из заметок для памяти) на форуме и обсудить их. Надеюсь, что они будут интересны участникам. Мне же это поможет увидеть недостатки текста, ответить на вопросы, о которых я сам не думал или ответы казались мне слишком очевидными.
По определенным соображениям, я планирую впервые опубликовать ряд моих научных идей в этой книге, а не в рецензируемых научных журналах. Это означает, что они будут обсуждаться сначала (до публикации книги) на данном форуме - открыто для всех. Соответственно, есть вероятность воровства этих идей. Единственным доказательством моего приоритета (и приоритета российской науки) являются дискуссии на этом форуме. Уважаемые посетители форума, все вы свидетели, что впервые прочитали это здесь. В начальный период развития науки, такое выкладывание на всеобщее обозрение было в порядке вещей (многие открытия были «опубликованы» всего лишь в форме писем от одного любителя науки к другому), но сейчас приоритеты устанавливаются публикацией в научных журналах. Я, можно сказать, возвращаюсь к этическим нормам начала науки.
Хотя изначально я такой цели не ставил, в ходе своей научной работы и размышлений я обнаружил множество серьезных ошибок и заблуждений в ряде наук. Мне придется поэтому значительное время посвятить "разоблачению" этих ошибок. Если разобраться, многие из них возникли из-за того, что человек, как правило, видит только то, на что ему сказали обратить внимание. Смотреть и видеть - разные вещи. Видеть реальность, видеть "очевидные", "бросающиеся в глаза" факты - очень трудно. Ярким примером такой особенности человеческой психики является это короткое видео, которое довольно известно (на английском). Для тех, кто английского не знает:
Показаны 8 баскетболистов, 4 в белой форме и 4 - в черной. Диктор спрашивает: "Сколько передач делает команда в белом?" И баскетболисты начинают бросать мячи друг другу. Сколько Вы насчитаете передач?
http://www.youtube.c…hg6qcgoay4
Первопроходцы, создатели науки зачастую определяют все последующее мышление поколений своих последователей, которые видят проблему строго в рамках, заданных отцами-основателями, не могут вырваться из колеи. Я надеюсь показать читателям ряд таких ошибок, ложных догм (и попытаюсь убедить их, что это именно ошибки). Я увидел их далеко не сразу - долгое время, я находился в плену тех же иллюзий, что и все остальные ученые. Уверен, что еще большее число "медведей" я не заметил. Я говорю не о мелких ошибках, неточностях, а о фундаментальных, исправление которых требует пересмотра всей данной науки. Например, почти всей науки о происхождении жизни. Например, почти всей физики.
Я не разрушитель по характеру и не садист, мне не доставляет никакого удовольствия выставлять людей, всю жизнь занимавшихся наукой, идиотами и показывать, что все, что они сделали в науке, ничего не стоит. Тем более что я так не думаю (что они идиоты и что их труд ничего не стоит). Тем не менее, такой может быть реакция общества и, в частности, политиков (когда мои идеи победят): "На что вы деньги народные потратили?" Что касается физики, то ответ простой - посмотрите вокруг себя, все технологии, которыми вы пользуетесь, созданы благодаря открытиям физиков.
На самом деле, большинство физиков должны только радоваться тому, что физика будет пересмотрена. Открывается огромное поле для новых открытий. Те физики, кто первыми успеют "переписать" старые разделы физики по-новому, вообще станут классиками науки - новые формулы будут носить их имена. То же и с происхождением жизни, с поиском и изучением новых форм жизни на Земле, которые я предсказываю. Пострадать, в какой-то степени, могут только крупные чиновники от науки, которые добивались выделения огромных денег на ускорители. Физика же как наука получит новый старт и новые возможности.
Я буду говорить о научных вопросах - или о "ненаучных" с научной точки зрения. Писать я буду как можно более простым языком, чтобы было понятно как можно более широкому кругу читателей. Злоупотреблять наукообразными терминами я не буду. Слишком много обзорной информации и объяснений терминов я, впрочем, давать не смогу - в интернете полно сайтов, где даются такие объяснения (достаточно кликнуть на термине правой кнопкой мыши и выбрать "искать в Google термин"). Но, в общем, представителям естественных наук и технарям (физикам, инженерам, химикам) большинство должно быть понятно.
Насчет копирайта: хотя это будет позднее опубликовано в виде книги (вероятно, со значительными добавлениями и исправлениями), перепечатки и распространение в некоммерческих целях моих статей с данного форума разрешены и приветствуются (с обязательной ссылкой на авторство и первоначальный источник - данный форум). Я больше заинтересован в максимальном эффекте от моего труда, чем в максимальной прибыли от публикации (что не означает, что я разрешаю бесплатные перепечатки в коммерческих целях).
P.S. Что касается ролика - после первого показа бросания мяча, диктор говорит: "Ответ - 13. Но видели ли Вы медведя с лунной походкой?" Повторяется видео и зритель, как правило, только при повторном просмотре, действительно, видит медведя. В конце сообщение: "Легко не заметить что-то, если ты не ищешь этого".
Отредактировано: Yuri Rus - 24 май 2011 19:48:35

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Для объявлений.
Будет время от времени меняться.
Разговор об этом начался здесь. Здесь и здесь я написал модераторам, о чем я планирую писать на своей ветке. Это чтобы дать вам представление о будущих темах.
Сейчас я пишу о Происхождении Жизни в Солнечной системе, займет еще какое-то время (думаю, несколько дней). Хочу выложить сразу связный текст, а не маленькие кусочки.
Добавление 13.3.2011: Поджог Ближнего Востока и Африки показывает, что времени до начала Третьей мировой войны, возможно, осталось очень мало. Целью этой войны, я полагаю, является отнюдь не разрешение экономического кризиса, а резкое уменьшение численности населения Земли и уничтожение многих народов. Включая, возможно, русский народ.
Я считаю, что одной из важнейших внутренних причин грядущей катастрофы является глубокая ошибочность современной физики, в особенности, теории относительности. Теория относительности постулирует, что движение быстрее скорости света невозможно и что по мере приближения скорости космического корабля к скорости света его масса будет стремиться к бесконечности, а следовательно, путешествия к другим планетам будут занимать либо тысячи лет, либо потребуют траты огромных ресурсов. Может быть, когда-нибудь станет возможным создать колонии человечества у других звезд, но колонии эти будут по сути изолированы от Земли и никакой торговли, обмена с колониями быть не может. Это означает, что большинство человечества навсегда будет приковано к Земле и решить демографическую проблему за счет отправки избыточного населения к другим звездам невозможно. Что правительствам надо беречь ресурсы Земли – от людей. Что надо резко уменьшить население Земли, иначе большинство ресурсов будет скоро (сто лет, тысяча, десять тысяч – это все равно скоро, с точки зрения вечности, которую большинство людей обречено провести на одной-единственной планетке) истрачено. Уменьшить – до миллиарда человек или даже меньше (Жак-Ив Кусто, например, считал, что население Земли не должно превышать 200 миллионов людей). Уменьшить – как можно скорее. С моей точки зрения, это и является настоящей целью МЭК, а вовсе не суетное желание американцев сохранить высокий уровень жизни или мировое доминирование.
Я считаю, что теория относительности неверна. Что полеты космических кораблей к звездам со скоростями, много большими скорости света, возможны, и это не потребует чудовищных ресурсов. Не крохотные горстки людей (тысячи человек), а большинство человечества сможет отправиться к звездам – если пожелает. Ресурсы сначала Солнечной системы, затем других звездных систем будут доступны людям – и перевозка тяжелых грузов (металлов и пр.) от дальних звезд будет вполне рентабельна. Неверна не только теория относительности, но и электродинамика, и квантовая механика. Но начну я с ТО – поскольку именно ТО приковывает человечество к Земле и запрещает полеты к звездам как способ решения проблемы роста населения и скорого исчерпания ресурсов.
Я не завершил эту работу, хотя основные идеи у меня появились довольно много лет назад. Дело в том, что физикой после окончания института (ФТФ НЭТИ) я занимался только урывками, возвращаясь к ней раз в несколько лет. И хотя сейчас я поставил себе целью сконцентрироваться именно на физике и за год закончить книгу, я по-прежнему могу уделять этому только маленькую часть своего времени, потому что надо еще зарабатывать на жизнь. А времени как раз может и не хватить. Если планета уже завтра будет в огне, будет ли у меня время и возможность спокойно, не торопясь, доделать всё? Так что – будь что будет – выложу на всеобщее обозрение хотя бы то, что я уже сделал. Быть может, эта публикация в конечном итоге сможет остановить уже запланированную катастрофу. Если мои идеи будут поняты и развиты, будут воплощены в реальные летательные аппараты, использующие искусственную гравитацию, это, будем надеяться, заставит задуматься тех "элитариев", кто уже принял решение "сократить человечество".
Если бы не МЭК, не пожар на Ближнем Востоке и в Африке, не землетрясение в Японии, я бы, наверно, раскачивался еще долгие годы, прежде чем опубликовал все это. Но далее ждать просто нельзя.
Будет время от времени меняться.
Разговор об этом начался здесь. Здесь и здесь я написал модераторам, о чем я планирую писать на своей ветке. Это чтобы дать вам представление о будущих темах.
Сейчас я пишу о Происхождении Жизни в Солнечной системе, займет еще какое-то время (думаю, несколько дней). Хочу выложить сразу связный текст, а не маленькие кусочки.
Добавление 13.3.2011: Поджог Ближнего Востока и Африки показывает, что времени до начала Третьей мировой войны, возможно, осталось очень мало. Целью этой войны, я полагаю, является отнюдь не разрешение экономического кризиса, а резкое уменьшение численности населения Земли и уничтожение многих народов. Включая, возможно, русский народ.
Я считаю, что одной из важнейших внутренних причин грядущей катастрофы является глубокая ошибочность современной физики, в особенности, теории относительности. Теория относительности постулирует, что движение быстрее скорости света невозможно и что по мере приближения скорости космического корабля к скорости света его масса будет стремиться к бесконечности, а следовательно, путешествия к другим планетам будут занимать либо тысячи лет, либо потребуют траты огромных ресурсов. Может быть, когда-нибудь станет возможным создать колонии человечества у других звезд, но колонии эти будут по сути изолированы от Земли и никакой торговли, обмена с колониями быть не может. Это означает, что большинство человечества навсегда будет приковано к Земле и решить демографическую проблему за счет отправки избыточного населения к другим звездам невозможно. Что правительствам надо беречь ресурсы Земли – от людей. Что надо резко уменьшить население Земли, иначе большинство ресурсов будет скоро (сто лет, тысяча, десять тысяч – это все равно скоро, с точки зрения вечности, которую большинство людей обречено провести на одной-единственной планетке) истрачено. Уменьшить – до миллиарда человек или даже меньше (Жак-Ив Кусто, например, считал, что население Земли не должно превышать 200 миллионов людей). Уменьшить – как можно скорее. С моей точки зрения, это и является настоящей целью МЭК, а вовсе не суетное желание американцев сохранить высокий уровень жизни или мировое доминирование.
Я считаю, что теория относительности неверна. Что полеты космических кораблей к звездам со скоростями, много большими скорости света, возможны, и это не потребует чудовищных ресурсов. Не крохотные горстки людей (тысячи человек), а большинство человечества сможет отправиться к звездам – если пожелает. Ресурсы сначала Солнечной системы, затем других звездных систем будут доступны людям – и перевозка тяжелых грузов (металлов и пр.) от дальних звезд будет вполне рентабельна. Неверна не только теория относительности, но и электродинамика, и квантовая механика. Но начну я с ТО – поскольку именно ТО приковывает человечество к Земле и запрещает полеты к звездам как способ решения проблемы роста населения и скорого исчерпания ресурсов.
Я не завершил эту работу, хотя основные идеи у меня появились довольно много лет назад. Дело в том, что физикой после окончания института (ФТФ НЭТИ) я занимался только урывками, возвращаясь к ней раз в несколько лет. И хотя сейчас я поставил себе целью сконцентрироваться именно на физике и за год закончить книгу, я по-прежнему могу уделять этому только маленькую часть своего времени, потому что надо еще зарабатывать на жизнь. А времени как раз может и не хватить. Если планета уже завтра будет в огне, будет ли у меня время и возможность спокойно, не торопясь, доделать всё? Так что – будь что будет – выложу на всеобщее обозрение хотя бы то, что я уже сделал. Быть может, эта публикация в конечном итоге сможет остановить уже запланированную катастрофу. Если мои идеи будут поняты и развиты, будут воплощены в реальные летательные аппараты, использующие искусственную гравитацию, это, будем надеяться, заставит задуматься тех "элитариев", кто уже принял решение "сократить человечество".
Если бы не МЭК, не пожар на Ближнем Востоке и в Африке, не землетрясение в Японии, я бы, наверно, раскачивался еще долгие годы, прежде чем опубликовал все это. Но далее ждать просто нельзя.
Отредактировано: Yuri Rus - 30 май 2011 20:19:12

Москва
25 лет
Карма: +0.16
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Уважаемые участники, у меня ко всем большая просьба.
Я хочу выложить некую критику ошибок физики, о чем я ранее упоминал. В качестве иллюстрации я планирую привести копии некоторых страниц из учебников, чтобы было видно, что это не я выдумал, а так написано именно в учебниках. Так вот, некоторые вещи я не могу найти в учебниках на русском языке - только на английском. Поскольку не все на форуме владеют английским, я бы, безусловно, хотел дать русский текст.
Подскажите, пожалуйста, в каких учебниках на русском языке есть подобная аргументация (я даю два варианта из двух книг):
1. Leigh Page, Introduction to Theoretical Physics, 1952.


2. Petr Beckman, Einstein Plus Two, 1987.


Меня интересует аргумент, что поле точечного заряда, движущегося с постоянной скоростью, в момент t + dt в точке x + vdt должно быть таким же, как в момент t в точке x, а следовательно,
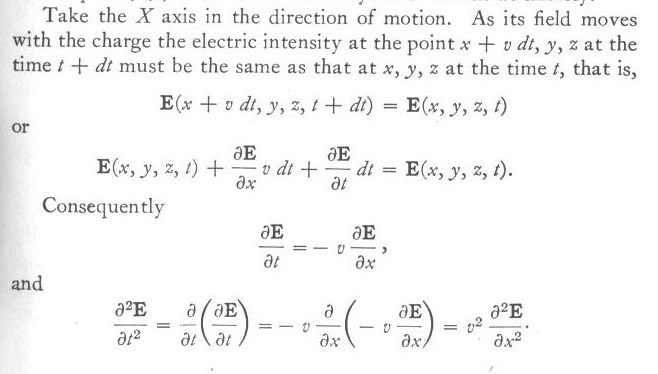
Я точно знаю, что это стандартный аргумент, нам его на лекциях давали, и я его раньше встречал в каких-то книгах на русском языке. Но сейчас, просмотрев более 100 русских учебников по электродинамике, теории относительности и мат. физике, я нигде этого не смог найти. Обычно сразу даются преобразования Лоренца и все.
Может быть, кто-то знает, в каком учебнике это есть - на русском? Можно, конечно, переводном с любого другого языка. Лучше всего, если эта книга есть в Колхозе или Library Genesis. Заранее спасибо!
Я хочу выложить некую критику ошибок физики, о чем я ранее упоминал. В качестве иллюстрации я планирую привести копии некоторых страниц из учебников, чтобы было видно, что это не я выдумал, а так написано именно в учебниках. Так вот, некоторые вещи я не могу найти в учебниках на русском языке - только на английском. Поскольку не все на форуме владеют английским, я бы, безусловно, хотел дать русский текст.
Подскажите, пожалуйста, в каких учебниках на русском языке есть подобная аргументация (я даю два варианта из двух книг):
1. Leigh Page, Introduction to Theoretical Physics, 1952.


2. Petr Beckman, Einstein Plus Two, 1987.


Меня интересует аргумент, что поле точечного заряда, движущегося с постоянной скоростью, в момент t + dt в точке x + vdt должно быть таким же, как в момент t в точке x, а следовательно,
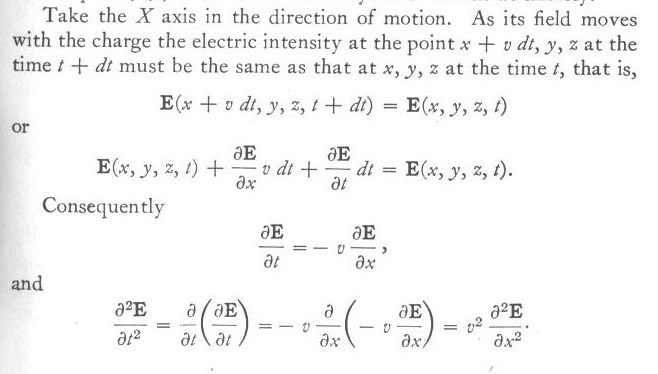
Я точно знаю, что это стандартный аргумент, нам его на лекциях давали, и я его раньше встречал в каких-то книгах на русском языке. Но сейчас, просмотрев более 100 русских учебников по электродинамике, теории относительности и мат. физике, я нигде этого не смог найти. Обычно сразу даются преобразования Лоренца и все.
Может быть, кто-то знает, в каком учебнике это есть - на русском? Можно, конечно, переводном с любого другого языка. Лучше всего, если эта книга есть в Колхозе или Library Genesis. Заранее спасибо!
Отредактировано: Yuri Rus - 21 ноя 2019 00:14:44
Карма: +147.41
Регистрация: 05.06.2010
Сообщений: 20,030
Читатели: 8
Регистрация: 05.06.2010
Сообщений: 20,030
Читатели: 8
Цитата: Yuri Rus от 12.03.2011 05:06:42
<skip>
Я точно знаю, что это стандартный аргумент, нам его на лекциях давали, и я его раньше встречал в каких-то книгах на русском языке. Но сейчас, просмотрев более 100 русских учебников по электродинамике, теории относительности и мат. физике, я нигде этого не смог найти. Обычно сразу даются преобразования Лоренца и все.
Может быть, кто-то знает, в каком учебнике это есть - на русском? Можно, конечно, переводном с любого другого языка. Лучше всего, если эта книга есть в Колхозе или Library Genesis. Заранее спасибо!
Может быть этот аргумент подойдет :
Цитата
Поле равномерно двигающегося заряда
Обратим внимание, что мы использовали постулат инвариантности зарядов частиц, оставив их неизменными в системе S. Это очень сильное допущение. Аналогично инвариантности массы, мы считаем, что заряд — это собственная характеристика объекта, не зависящая от его скорости.

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Цитата: Поверонов от 12.03.2011 23:36:18Может быть этот аргумент подойдет :
Спасибо, но здесь с самого начала вводятся преобразования Лоренца. Мне нужно именно как здесь, без изменений:
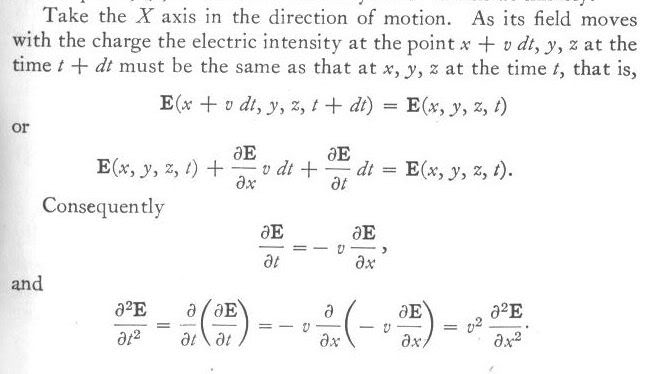
Я могу, конечно, привести именно эти ссылки и дать короткий перевод. Но хотелось источник на русском языке.
Отредактировано: Yuri Rus - 21 ноя 2019 00:17:01
Карма: +147.41
Регистрация: 05.06.2010
Сообщений: 20,030
Читатели: 8
Регистрация: 05.06.2010
Сообщений: 20,030
Читатели: 8
Цитата: Yuri Rus от 13.03.2011 04:38:24
Спасибо, но здесь с самого начала вводятся преобразования Лоренца. Мне нужно именно как здесь, без изменений:
Я могу, конечно, привести именно эти ссылки и дать короткий перевод. Но хотелось источник на русском языке.
Но в тексте по английски отсутствует какая-либо аргументация используемого равенства. Просто сказано "must be the same" = "ДОЛЖНЫ быть идентичны". Это не обоснование.

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Цитата: Поверонов от 13.03.2011 10:42:03
Но в тексте по английски отсутствует какая-либо аргументация используемого равенства. Просто сказано "must be the same" = "ДОЛЖНЫ быть идентичны". Это не обоснование.
Да нет, идентичны-то они идентичны - я имею в виду
E(x+vdt,y,z,t+dt) = E(x,y,z,t)
Далее автор пользуется определением полного дифференциала (или полной производной по времени) и из него получает
E(x+vdt,y,z,t+dt) = E(x,y,z,t) + (dE/dx)vdt + (dE/dt)dt
(dE/dx и dE/dt - частные производные)
А вот это как раз неверно, и именно это я хотел "разоблачить".
Отредактировано: Yuri Rus - 12 апр 2011 13:13:23

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Цитата: SvK
Преобразования Лоренца, как обоснование великого надувательства,приведены тут:
http://www.dialectic…0110ru.htm
Ув. SvK, автор - Вы? То есть Л.Г.К.?
Так или иначе, я полагаю, что математически и логически теория относительности, преобразования Лоренца, пространство Минковского с 4-векторами безупречны и ошибок не содержат. Потому искать там противоречия бессмысленно.
Тем не менее, они неверны - потому что не соответсвуют реальному физическому миру, в котором мы живем. Математика ведь совсем не обязана соответствовать реальному миру, поскольку математика способна описать множество разных миров, в основе которых лежат разные аксиомы. Пример - разные геометрии (Эвклида, Лобачевского, Минковского, Римана, и миллионы других), которые внутренне непротиворечивы и подчиняются своим собственным законам, однако реальный мир описывает только одна из них.
Теория относительности неверна, потому что неверны уравнения Максвелла. Уравнения Максвелла неверны, потому что неверно волновое уравнение. Именно об этом я и собираюсь говорить. Надо сначала разобраться с распространением волн, а потом уже можно строить электродинамику, интерпретировать эксперимент Майкельсона и т.д.
Но волновое уравнение лежит в основе почти всей физики. Собственно, именно с него математическая физика и началась - еще в XVIII веке произошел знаменитый "спор о струне" между Ж.Л. Д’Аламбером, Л. Эйлером. Д. Бернулли и Ж.Л. Лагранжем
(http://ru.wikipedia.…0%BD%D0%B5)
Он оказал огромное влияние на все последующее развитие мат. физики (не зря учебники по мат. физики обычно начинаются именно с рассмотрения колебаний струны). Ошибка, на мой взгляд, произошла при переходе от формулы Пуассона (для линейного однородного волнового уравнения) к уравнению с запаздывающими потенциалами (для линейного НЕоднородного волнового уравнения). Если я не ошибаюсь, первым получил уравнение для запаздывающих потенциалов Ж. Дюамель в XIX веке, точную дату не знаю.
(http://ru.wikipedia.…0%BB%D1%8F)
Это уравнение должно быть принципиально нелинейным, а физика с тех самых пор использует линейные уравнения. Кроме того, физика злоупотребляет линейными однородными уравнениями (то есть без источников, без внешних сил), которые способны описать только поведение самой среды, например, свободные колебания среды, но не способны описать, допустим, распространение волн от источников. Выводы же, тем не менее, распространяются на поведение систем с источниками. В результате не только электродинамика, но и большая часть гидродинамики и акустики попросту неверны. В общем, взять бы этого Дюамеля, да за такие доказательства года на три в Соловки!
Конечно, не он "главный виновник" ошибок физики. Сам математический подход неверен - находить сначала решение простой задачи и затем всеми силами пытаться свести решение более сложной задачи к решению этой простой задачи. При этом, слишком часто оказываются незамеченными принципиально иные особенности этой более сложной задачи. В частности, для волнового уравнения - принципиальная нелинейность его решения оказывается незамеченной и распространение волн предполагается линейным.
Я планирую показать, в частности, что при движении любого источника волн (акустических, световых и т.д.) лучи будут обязательно искривляться. Это, в частности, объясняет, почему в эксперименте майкельсона не было (и в такой постановке эксперимента - не может быть) замечено движение Земли относительно эфира. Последовательные волны от источника обязательно взаимодействуют друг с другом, изменяют направление движения друг друга. При этом, при движении источника продольных волн обязательно появятся поперечные компоненты, распространяющиеся с той же скоростью. При движении источника поперечных волн, аналогично, появятся продольные компоненты, распространяющиеся с той же скоростью.
Это касается и акустики - по мере приближения скорости источника звука с скорости звука в воздухе поперечные, вихревые компоненты звуковых волн должны быть очень заметными, равно как и эффект искривления лучей звука будет все более выраженным. Это очень легко проверить - для звука.
В ближайшее время я все это обосную.
Карма: +147.41
Регистрация: 05.06.2010
Сообщений: 20,030
Читатели: 8
Регистрация: 05.06.2010
Сообщений: 20,030
Читатели: 8
Цитата: Yuri Rus от 13.03.2011 17:43:10
Далее автор пользуется определением производной (или полного дифференциала по времени) и из него получает
E(x+vdt,y,z,t+dt) = E(x,y,z,t) + (dE/dx)vdt + (dE/dt)dt
(dE/dx и dE/dt - частные производные)
А вот это как раз неверно, и именно это я хотел "разоблачить".
Так в этом преобразовании вроде уже нет физических оснований, а только чистая математика:
Формула полного дифференциала:
E(x+dx,y,z,t+dt) = E(x,y,z,t) + (dE/dx)dx + (dE/dt)dt
dx=vdt, так как v - константа, тогда имеем
E(x+vdt,y,z,t+dt) = E(x,y,z,t) + (dE/dx)vdt + (dE/dt)dt
В чем подвох ?

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Цитата: Поверонов от 13.03.2011 23:36:02
Так в этом преобразовании вроде уже нет физических оснований, а только чистая математика:
Формула полного дифференциала:
E(x+dx,y,z,t+dt) = E(x,y,z,t) + (dE/dx)dx + (dE/dt)dt
dx=vdt, так как v - константа, тогда имеем
E(x+vdt,y,z,t+dt) = E(x,y,z,t) + (dE/dx)vdt + (dE/dt)dt
В чем подвох ?
Вот именно - "чистая математика". Об этом я и хочу говорить - как "чистая математика" приводит к совершенно неверным выводам. Мне для этого понадобится некоторое время, все написать.

Москва
25 лет
Карма: +0.16
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0
вот тут нашел, достаточно много учебников по физике,
http://alexandr4784.…hyzikc.htm
в том числе и Сивухин по которому я учился, но в том виде как надо, я здесь этого не нашел...
http://alexandr4784.…hyzikc.htm
в том числе и Сивухин по которому я учился, но в том виде как надо, я здесь этого не нашел...

Москва
Карма: +1.82
Регистрация: 20.03.2009
Сообщений: 59
Читатели: 0
Регистрация: 20.03.2009
Сообщений: 59
Читатели: 0
Цитата: Yuri Rus от 13.03.2011 04:38:24
Я хочу выложить некую критику ошибок физики, о чем я ранее упоминал. В качестве иллюстрации я планирую привести копии некоторых страниц из учебников, чтобы было видно, что это не я выдумал, а так написано именно в учебниках. Так вот, некоторые вещи я не могу найти в учебниках на русском языке - только на английском. Поскольку не все на форуме владеют английским, я бы, безусловно, хотел дать русский текст.
Я могу, конечно, привести именно эти ссылки и дать короткий перевод.
Так и нужно сделать. Зачем связывать публикование концепции с поиском ссылок, удобоваримых для всех. Приводите английские, формально вы этим выполните требования форума. Кроме того, согласитесь, учебник с формулами - это не беллетристика, которая доступна для перевода только со словарем..
Публикуйте концепцию, сударь, а ссылки, если что, мы сообща подтащим. Или она у вас не готова и вы просто поторопились с заявлением? Тогда так и скажите, мы подождем.
Не скрою. Удивлён..

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Цитата: TIR от 19.03.2011 13:32:32
Так и нужно сделать. Зачем связывать публикование концепции с поиском ссылок, удобоваримых для всех. Приводите английские, формально вы этим выполните требования форума. Кроме того, согласитесь, учебник с формулами - это не беллетристика, которая доступна для перевода только со словарем..
Публикуйте концепцию, сударь, а ссылки, если что, мы сообща подтащим. Или она у вас не готова и вы просто поторопились с заявлением? Тогда так и скажите, мы подождем.
Я хотел начать с происхождения жизни в Солнечной системе, и потратил значительную часть времени на написание моей теории этого процесса, но в связи с тем, что происходит в мире (пожар на Ближнем Востоке и в Африке, землетрясение в Японии), решил, что необходимо опубликовать мою физическую концепцию как можно скорее. Потом может быть слишком поздно.
Дело в том, что на меня сейчас одновременно навалилось сразу множество проблем и писать просто нет времени и сил. Пока писал, запустил свои финансовые дела, сейчас совершенно нет денег и приходится их тупо зарабатывать, просто чтобы выжить. Я, так сказать, кустарь-одиночка. Фиксированную зарплату не получаю - чтобы было чем платить за жилье и оплачивать бизнес-расходы, надо каждую неделю суетиться и что-то продавать. Вот сейчас я этим и вынужден заниматься. И много других проблем.
Кроме того, не хочется выкладывать по маленькому кусочку, по одной-две страницы. Это же не, допустим, история или худлит. Здесь лучше выложить хоть сколько-нибудь законченный фрагмент.

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Поехали!
Поздравляю всех с Праздником - 50-летием полета Юрия Гагарина и Днем Космонавтики!
В связи с этим, решил начать выкладывать свои идеи именно сегодня. Немного позже выложу еще, что успею написать.
Это совсем не так просто; главный вопрос – как писать? Если я начну долго и нудно разбирать ошибки дифференциальных уравнений в частных производных, это может показаться читателям слишком скучным и малозначительным, и нить рассуждений может быть потеряна. Пожалуй, я начну сразу с неких выводов, в как можно более простой и доходчивой форме, чтобы было понятно, какую альтернативу я предлагаю, и лишь потом будудолго и нудно последовательно разбирать ошибки существующего мат. аппарата физики. Потом опять – что нужно исправить, какой должна быть математика физики.
Надеюсь, моя попытка не закончится так же, как у моего предшественника:
…Попытки поэта сочинить заявление насчет страшного консультанта не привели ни к чему. Лишь только он получил от толстой фельдшерицы, которую звали Прасковьей Федоровной, огрызок карандаша и бумагу, он деловито потер руки и торопливо пристроился к столику. Начало он вывел довольно бойко:
К тому времени, как появилась издалека пугающая туча с дымящимися краями и накрыла бор и дунул ветер, Иван почувствовал, что обессилел, что с заявлением ему не совладать, не стал поднимать разлетевшихся листков и тихо и горько заплакал.
В чем заключается моя цель? Я хочу доказать, что математический аппарат, используемый мат. физикой, не адекватен реальному физическому миру и физическим проблемам. Как следствие, большинство уравнений физики неверны. Я не успел полностью закончить эту работу, но уже того, что я хочу выложить здесь на форуме, должно быть достаточно, чтобы доказать фундаментальную ошибочность математических основ физики и наметить пути построения нового математического аппарата. Кроме того, я совсем не уверен, что мне следует выкладывать в открытый доступ всё, что я обнаружил. Знание – сила, не стоит забывать этого. И если эта сила попадет не в те руки, 2012 действительно может стать годом катастрофы.
Лет 20 назад, мне попалось на глаза интервью с математиком, председателем или членом комиссии по доказательствам Великой Теоремы Ферма. Он сказал, что комиссия эта даже не рассматривает те попытки доказательств, которые используют слишком простой мат. аппарат. А писем с такими попытками им приходит много.
Однажды даже пришла телеграмма:
«Перенесите bn в правую часть!»
Мое доказательство ошибочности мат. физики – примерно на таком же уровне сложности. И потому принять его многим физикам будет очень нелегко (вначале, по крайней мере). Дело в том, что речь идет о настолько простых, привычных понятиях, которые проходились еще в школе, которые въелись в подкорку, стали рефлексами, что остановиться, задуматься о них – это совсем не просто. Возможно, легче будет понять меня не действующим физикам (особенно преподавателям мат. физики или электродинамики), а «бывшим», скажем, выпускникам физтеха или физфака, которые в девяностые вынуждены были бросить науку, но физики по крайней мере не боятся и, открыв учебник, легко восстановят свои знания. Именно потому, что они не имели с физикой дела много лет, у них будет свежий взгляд. А поскольку они более не студенты, а зрелые, самостоятельные люди, привыкшие доверять собственному мнению, на них не будет более давления авторитетов профессоров или классиков. Это, если что, я не подлизываюсь к участникам форума, где таких много; я сам через это прошел. Только тогда, когда я уже не был студентом, когда мои достижения в других областях укрепили мое доверие к собственному мнению, я смог непредвзято посмотреть на физику и увидеть проблемы там, где я ранее полагался на мнение авторитетов.
Поскольку я не ожидаю быстрого принятия моих идей от профессионального физического сообщества, я ориентируюсь на любителей физики, не владеющих слишком сложным математическим аппаратом. Писать я поэтому стараюсь очень просто, с подробными разъяснениями каждой детали. Понять меня сможет любой неглупый старшеклассник или первокурсник физической специальности (а не понять – профессиональные физики).
Поздравляю всех с Праздником - 50-летием полета Юрия Гагарина и Днем Космонавтики!
В связи с этим, решил начать выкладывать свои идеи именно сегодня. Немного позже выложу еще, что успею написать.
Это совсем не так просто; главный вопрос – как писать? Если я начну долго и нудно разбирать ошибки дифференциальных уравнений в частных производных, это может показаться читателям слишком скучным и малозначительным, и нить рассуждений может быть потеряна. Пожалуй, я начну сразу с неких выводов, в как можно более простой и доходчивой форме, чтобы было понятно, какую альтернативу я предлагаю, и лишь потом буду
Надеюсь, моя попытка не закончится так же, как у моего предшественника:
…Попытки поэта сочинить заявление насчет страшного консультанта не привели ни к чему. Лишь только он получил от толстой фельдшерицы, которую звали Прасковьей Федоровной, огрызок карандаша и бумагу, он деловито потер руки и торопливо пристроился к столику. Начало он вывел довольно бойко:
«В милицию. Члена МАССОЛИТа Ивана Николаевича Бездомного. Заявление. Вчера вечером я пришел с покойным М. А. Берлиозом на Патриаршие пруды...»
И сразу поэт запутался, главным образом из-за слова «покойным». С места выходила какая-то безлепица: как это так – пришел с покойным? Не ходят покойники! Действительно, чего доброго, за сумасшедшего примут!
Подумав так, Иван Николаевич начал исправлять написанное. Вышло следующее: «...с М. А. Берлиозом, впоследствии покойным...». И это не удовлетворило автора. Пришлось применить третью редакцию, а та оказалась еще хуже первых двух: «...Берлиозом, который попал под трамвай...» – а здесь еще прицепился этот никому не известный композитор-однофамилец, и пришлось вписать: «...не композитором...»
Намучавшись с этими двумя Берлиозами, Иван все зачеркнул и решил начать сразу с чего-то очень сильного, чтобы немедленно привлечь внимание читающего, и написал, что кот садился в трамвай, а потом вернулся к эпизоду с отрезанной головой. Голова и предсказание консультанта привели его к мысли о Понтии Пилате, и для вящей убедительности Иван решил весь рассказ о прокураторе изложить полностью с того самого момента, как тот в белом плаще с кровавым подбоем вышел в колоннаду иродова дворца.
Иван работал усердно и перечеркивал написанное, и вставлял новые слова, и даже попытался нарисовать Понтия Пилата, а затем кота на задних лапах. Но и рисунки не помогли, и чем дальше – тем путанее и непонятнее становилось заявление поэта.
К тому времени, как появилась издалека пугающая туча с дымящимися краями и накрыла бор и дунул ветер, Иван почувствовал, что обессилел, что с заявлением ему не совладать, не стал поднимать разлетевшихся листков и тихо и горько заплакал.
В чем заключается моя цель? Я хочу доказать, что математический аппарат, используемый мат. физикой, не адекватен реальному физическому миру и физическим проблемам. Как следствие, большинство уравнений физики неверны. Я не успел полностью закончить эту работу, но уже того, что я хочу выложить здесь на форуме, должно быть достаточно, чтобы доказать фундаментальную ошибочность математических основ физики и наметить пути построения нового математического аппарата. Кроме того, я совсем не уверен, что мне следует выкладывать в открытый доступ всё, что я обнаружил. Знание – сила, не стоит забывать этого. И если эта сила попадет не в те руки, 2012 действительно может стать годом катастрофы.
Лет 20 назад, мне попалось на глаза интервью с математиком, председателем или членом комиссии по доказательствам Великой Теоремы Ферма. Он сказал, что комиссия эта даже не рассматривает те попытки доказательств, которые используют слишком простой мат. аппарат. А писем с такими попытками им приходит много.
Однажды даже пришла телеграмма:
«Перенесите bn в правую часть!»
Мое доказательство ошибочности мат. физики – примерно на таком же уровне сложности. И потому принять его многим физикам будет очень нелегко (вначале, по крайней мере). Дело в том, что речь идет о настолько простых, привычных понятиях, которые проходились еще в школе, которые въелись в подкорку, стали рефлексами, что остановиться, задуматься о них – это совсем не просто. Возможно, легче будет понять меня не действующим физикам (особенно преподавателям мат. физики или электродинамики), а «бывшим», скажем, выпускникам физтеха или физфака, которые в девяностые вынуждены были бросить науку, но физики по крайней мере не боятся и, открыв учебник, легко восстановят свои знания. Именно потому, что они не имели с физикой дела много лет, у них будет свежий взгляд. А поскольку они более не студенты, а зрелые, самостоятельные люди, привыкшие доверять собственному мнению, на них не будет более давления авторитетов профессоров или классиков. Это, если что, я не подлизываюсь к участникам форума, где таких много; я сам через это прошел. Только тогда, когда я уже не был студентом, когда мои достижения в других областях укрепили мое доверие к собственному мнению, я смог непредвзято посмотреть на физику и увидеть проблемы там, где я ранее полагался на мнение авторитетов.
Поскольку я не ожидаю быстрого принятия моих идей от профессионального физического сообщества, я ориентируюсь на любителей физики, не владеющих слишком сложным математическим аппаратом. Писать я поэтому стараюсь очень просто, с подробными разъяснениями каждой детали. Понять меня сможет любой неглупый старшеклассник или первокурсник физической специальности (а не понять – профессиональные физики).
Отредактировано: Yuri Rus - 05 янв 2022 16:00:21

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Я буду в основном говорить о волнах и волновом уравнении. Отмечу, что уравнения динамики жидкости и твердого тела в классической механике обычно выражаются в двух формах – лагранжевой и эйлеровой. Уравнения в форме Лагранжа описывают движения индивидуальной частицы жидкости или твердого тела (точнее, некоторого элемента объема, состоящего из многих частиц). Координаты (x, y, z) частицы считаются функциями времени и трех параметров (a, b, c), в качестве которых часто выбираются координаты частицы при t = 0. Уравнения в форме Эйлера описывают то, что происходит в некоторой точке пространства (x, y, z) (точнее, с неким бесконечно малым элементом длины, поверхности или объема) на протяжении некоторого промежутка времени. Рассматриваются силы, скорости, смещения и т.д. применительно именно к этому малому элементу, и для него выводятся дифференциальные уравнения. Для полного описания поведения системы, задаются еще начальные и граничные условия.
Я предлагаю третий подход. Вместо того, чтобы рассматривать силы, скорости и смещения некого элемента среды (или некой частицы), расположенного в произвольной точке пространства, мы будем начинать анализ распространения волн с их источника. Есть источник, он создает какую-то силу, действующую на окружающие его элементы среды (которые не расположены где-то далеко, а прямо и непосредственно контактируют с источником), эта сила вызывает смещение этих элементов, которые приобретают ускорение, скорость, далее они воздействуют на соседние с ними элементы среды, и т.д. Причем, что важно с физической точки зрения – источник создает не единичную волну, которая затем распространяется по покоящейся среде, а множество волн, непрерывно генерирует их. Кроме того, если мы хотим обсудить теорию относительности, мы должны рассмотреть движение источника относительно среды.
Однако, прежде чем приступить к этой задаче, нам необходимо рассмотреть само понятие функции, ее производной и дифференциала. Как ни дико это звучит, физика оперирует неверными определениями полного дифференциала, дивергенции, ротора и т.п. Неудивительно, что такие ошибки делают почти все уравнения физики полностью неверными.
Я покажу это на нескольких простых примерах. Очевидно, что вместо частных примеров, это все легко написать в общей форме, но мне кажется, что на конкретных примерах эти принципы будет легче понять. Позже это будет переписано в более строгой, более формальной форме, сейчас же я просто хочу донести свои мысли до первой аудитории.
Нас будут интересовать только гладкие функции. Что такое функция от одного аргумента? Скажем, функция y = 3x₃? Она представляет собой кривую линию, проходящую через ноль. Ее производная dy/dx = 9х₂. Каждому значению x соответствует определенное значение y. Но: не каждой точке с координатами (х, у) соответствует какое-то значение кривой y = 3x₃. Большинство точек на плоскости (х, у) – «пустые».
А сейчас рассмотрим другую кривую: y = 3(x – 2)₃. Она выглядит точно так же, как y = 3x₃, но сдвинута относительно нее вправо на две единицы. Аналогично ведут себя функции
y = 3(x – 3.3)₃
y = 3(x – 5.4)₃
y = 3(x – 83.23)₃
Они сдвинуты относительно функции y = 3x₃ вправо на 3.3, 5.4 и 83.23, соответственно. Очевидно, что все эти кривые образуют семейство функций, которые описываются формулой y = 3(x – u)₃, где u – это другая непрерывная переменная. Варьируя u, мы получаем, что теперь через каждую точку на плоскости (х, у) проходит какая-то кривая из семейства y = 3(x – u)₃. Заметим, что на плоскости (x, y) – это разные кривые, разные функции. Однако, если мы сообразим, что y = 3(x – u)₃ – это функция от двух аргументов x и u, а не от одного только x, то мы можем изобразить зависимость y(x, u) уже не на плоскости (x, y), а в трехмерном пространстве (x, u, y), причем теперь это не семейство функций, а одна функция. Назовем такую функцию y(x, u) в трехмерном пространстве полной функцией (full, or total function), а индивидуальные функции y(x, u) в двухмерном пространстве – единичными функциями (singular functions). (((Вопрос к аудитории: какой термин лучше – единичная функция или индивидуальная функция?))) Для каждой единичной функции, u – это константа. Обозначим ее как uc, чтобы отличать единичные функции y(x, uc) с постоянным значением uc от полной функции y(x, u) с переменной u.
Только в этом трехмерном пространстве будут иметь смысл полный дифференциал Dy и частные производные ∂y/∂x и ∂y/∂u:
Dy = (∂y/∂x)dx + (∂y/∂u)du = 9(x – u)₂dx – 9(x – u)₂du = 9(x – u)₂(dx – du)
Если же мы, по какой-то причине, не хотим считать u независимой переменной и полагаем, что y - это функция только от x, упорно изображая все семейство кривых y = 3(x – uc)₃ на плоскости (x, y), то, разумеется, ни о каком полном дифференциале Dy мы даже задумываться не будем. Есть только производная от y по x, и точка. При этом, хотя мы теперь можем найти производную dy(x)/dx для любой точки плоскости (x, y), то есть «пустых» точек на этой плоскости больше нет, эти производные на самом деле принадлежат разным единичным функциям y(x, uc), поскольку значения uc у них разные.
Рассмотрим теперь функции вида
y = 3(x – 2)₃ + 2
y = 3(x – 5.4)₃ + 7.83
y = 3(x – 83.23)₃ + 4.125
и т.д.
Заметим, что это семейство функций мы тоже можем нарисовать на одной плоскости (x, y). Очевидно, они образуют другое семейство кривых вида y = 3(x – u)₃ + p, которые сдвинуты вверх на величину p по сравнению с y = 3(x – u)₃. Подчеркнем, что на одной плоскости это разные единичные функции. Только в четырехмерном пространстве (x, u, p, y) одна-единственная функция y(x, u, p) будет описывать все значения u и p. Поэтому она и является полной.
В этом четырехмерном пространстве, полный дифференциал Dy(x, u, p) будет равен:
Dy(x, u, p) = (∂y/∂x)dx + (∂y/∂u)du + (∂y/∂p)dp = 9(x – u)₂dx – 9(x – u)₂du + dp
Заметим, что если мы изобразим функцию y = 3(x – u)₃ + p не в четырехмерном, а в трехмерном пространстве (x, p, y), где разным значениям uc соответствуют разные функции y(x, uc, p), то в этом случае мы тоже можем говорить о дифференциалах dy(x, uc, p), но эти дифференциалы – разные для разных единичных функций y(x, uc, p). Например, для y = 3(x – 2)₃ + p и y = 3(x – 6.73)₃ + p они будут равны:
dy(x, 2, p) = (∂y(x, 2, p)/∂x)dx + (∂y(x, 2, p)/∂p)dp = 9(x – 2)₂dx + dp
dy(x, 6.73, p) = (∂y(x, 6.73, p)/∂x)dx + (∂y(x, 6.73, p)/∂p)dp = 9(x – 6.73)₂dx + dp
Соответственно, в трехмерном пространстве (x, p, y) рассматриваться эти дифференциалы должны по отдельности для каждой функции y(x, uc, p). Назовем такие дифференциалы не полными, а единичными (singular differentials). (((Я бы, возможно, предпочел использовать термин частные дифференциалы, но он уже занят.)))
Я предлагаю третий подход. Вместо того, чтобы рассматривать силы, скорости и смещения некого элемента среды (или некой частицы), расположенного в произвольной точке пространства, мы будем начинать анализ распространения волн с их источника. Есть источник, он создает какую-то силу, действующую на окружающие его элементы среды (которые не расположены где-то далеко, а прямо и непосредственно контактируют с источником), эта сила вызывает смещение этих элементов, которые приобретают ускорение, скорость, далее они воздействуют на соседние с ними элементы среды, и т.д. Причем, что важно с физической точки зрения – источник создает не единичную волну, которая затем распространяется по покоящейся среде, а множество волн, непрерывно генерирует их. Кроме того, если мы хотим обсудить теорию относительности, мы должны рассмотреть движение источника относительно среды.
Однако, прежде чем приступить к этой задаче, нам необходимо рассмотреть само понятие функции, ее производной и дифференциала. Как ни дико это звучит, физика оперирует неверными определениями полного дифференциала, дивергенции, ротора и т.п. Неудивительно, что такие ошибки делают почти все уравнения физики полностью неверными.
Я покажу это на нескольких простых примерах. Очевидно, что вместо частных примеров, это все легко написать в общей форме, но мне кажется, что на конкретных примерах эти принципы будет легче понять. Позже это будет переписано в более строгой, более формальной форме, сейчас же я просто хочу донести свои мысли до первой аудитории.
Нас будут интересовать только гладкие функции. Что такое функция от одного аргумента? Скажем, функция y = 3x₃? Она представляет собой кривую линию, проходящую через ноль. Ее производная dy/dx = 9х₂. Каждому значению x соответствует определенное значение y. Но: не каждой точке с координатами (х, у) соответствует какое-то значение кривой y = 3x₃. Большинство точек на плоскости (х, у) – «пустые».
А сейчас рассмотрим другую кривую: y = 3(x – 2)₃. Она выглядит точно так же, как y = 3x₃, но сдвинута относительно нее вправо на две единицы. Аналогично ведут себя функции
y = 3(x – 3.3)₃
y = 3(x – 5.4)₃
y = 3(x – 83.23)₃
Они сдвинуты относительно функции y = 3x₃ вправо на 3.3, 5.4 и 83.23, соответственно. Очевидно, что все эти кривые образуют семейство функций, которые описываются формулой y = 3(x – u)₃, где u – это другая непрерывная переменная. Варьируя u, мы получаем, что теперь через каждую точку на плоскости (х, у) проходит какая-то кривая из семейства y = 3(x – u)₃. Заметим, что на плоскости (x, y) – это разные кривые, разные функции. Однако, если мы сообразим, что y = 3(x – u)₃ – это функция от двух аргументов x и u, а не от одного только x, то мы можем изобразить зависимость y(x, u) уже не на плоскости (x, y), а в трехмерном пространстве (x, u, y), причем теперь это не семейство функций, а одна функция. Назовем такую функцию y(x, u) в трехмерном пространстве полной функцией (full, or total function), а индивидуальные функции y(x, u) в двухмерном пространстве – единичными функциями (singular functions). (((Вопрос к аудитории: какой термин лучше – единичная функция или индивидуальная функция?))) Для каждой единичной функции, u – это константа. Обозначим ее как uc, чтобы отличать единичные функции y(x, uc) с постоянным значением uc от полной функции y(x, u) с переменной u.
Только в этом трехмерном пространстве будут иметь смысл полный дифференциал Dy и частные производные ∂y/∂x и ∂y/∂u:
Dy = (∂y/∂x)dx + (∂y/∂u)du = 9(x – u)₂dx – 9(x – u)₂du = 9(x – u)₂(dx – du)
Если же мы, по какой-то причине, не хотим считать u независимой переменной и полагаем, что y - это функция только от x, упорно изображая все семейство кривых y = 3(x – uc)₃ на плоскости (x, y), то, разумеется, ни о каком полном дифференциале Dy мы даже задумываться не будем. Есть только производная от y по x, и точка. При этом, хотя мы теперь можем найти производную dy(x)/dx для любой точки плоскости (x, y), то есть «пустых» точек на этой плоскости больше нет, эти производные на самом деле принадлежат разным единичным функциям y(x, uc), поскольку значения uc у них разные.
Рассмотрим теперь функции вида
y = 3(x – 2)₃ + 2
y = 3(x – 5.4)₃ + 7.83
y = 3(x – 83.23)₃ + 4.125
и т.д.
Заметим, что это семейство функций мы тоже можем нарисовать на одной плоскости (x, y). Очевидно, они образуют другое семейство кривых вида y = 3(x – u)₃ + p, которые сдвинуты вверх на величину p по сравнению с y = 3(x – u)₃. Подчеркнем, что на одной плоскости это разные единичные функции. Только в четырехмерном пространстве (x, u, p, y) одна-единственная функция y(x, u, p) будет описывать все значения u и p. Поэтому она и является полной.
В этом четырехмерном пространстве, полный дифференциал Dy(x, u, p) будет равен:
Dy(x, u, p) = (∂y/∂x)dx + (∂y/∂u)du + (∂y/∂p)dp = 9(x – u)₂dx – 9(x – u)₂du + dp
Заметим, что если мы изобразим функцию y = 3(x – u)₃ + p не в четырехмерном, а в трехмерном пространстве (x, p, y), где разным значениям uc соответствуют разные функции y(x, uc, p), то в этом случае мы тоже можем говорить о дифференциалах dy(x, uc, p), но эти дифференциалы – разные для разных единичных функций y(x, uc, p). Например, для y = 3(x – 2)₃ + p и y = 3(x – 6.73)₃ + p они будут равны:
dy(x, 2, p) = (∂y(x, 2, p)/∂x)dx + (∂y(x, 2, p)/∂p)dp = 9(x – 2)₂dx + dp
dy(x, 6.73, p) = (∂y(x, 6.73, p)/∂x)dx + (∂y(x, 6.73, p)/∂p)dp = 9(x – 6.73)₂dx + dp
Соответственно, в трехмерном пространстве (x, p, y) рассматриваться эти дифференциалы должны по отдельности для каждой функции y(x, uc, p). Назовем такие дифференциалы не полными, а единичными (singular differentials). (((Я бы, возможно, предпочел использовать термин частные дифференциалы, но он уже занят.)))

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Эти совершенно тривиальные рассуждения имеют самое прямое отношение к волновому уравнению (и вообще ко всем дифференциальным уравнениям физики), как вы вскоре убедитесь. Сейчас же мы рассмотрим волновое уравнение несколько другого вида (оно используется в школьных учебниках и в университетских учебниках для нефизиков), которое описывает распространение фронта волны:
x₂ + y₂ + z₂ = c₂t₂
Это уравнение, возможно, не столь «научно», как волновое уравнение в частных производных:
∂₂u/∂t₂ – c₂∇₂u = K(x, y, z, t)
Но оно имеет то преимущество, что оно очень наглядно. Будем его использовать как «нулевое приближение», как «контроль на физический смысл», для качественной оценки волновых процессов. С ним труднее сделать ошибки.
Легко увидеть, что уравнение x₂ + y₂ + z₂ = c₂t₂ описывает распространение фронта сферической волны, которая была испущена из точки с координатами (0, 0, 0) в момент времени t = 0. Чем больше t, тем больше сфера с радиусом r = (x₂ + y₂ + z₂)₀.₅ = ct.
Но ведь волны – это не один только импульс в нулевой момент времени, правильно? А как нам описать распространение волны, испущенной в момент t₁? А мы только что разбирали похожий пример – как:
x₂ + y₂ + z₂ = c₂(t – t₁)₂
Подчеркнем, что это – другая волна, другая единичная функция, если мы пользуемся только четырехмерным пространством (x, y, z, t).
Теперь предположим, что источник движется с произвольной скоростью v в произвольном направлении и излучает волны, одну за другой. Как мы можем описать это семейство волн? Распространение каждой волны, испущенной в точке с координатами (ξ, η, ζ) в момент времени ԏ, будет удовлетворять следующему уравнению:
(x – ξ)₂ + (y – η)₂ + (z – ζ)₂ = c₂(t – ԏ)₂
или
r – rи = c(t – ԏ),
где r – это радиус-вектор (из начала координат) какой-либо точки распространяющейся волны в момент t, rи – радиус-вектор источника волн в момент ԏ.
Подчеркнем, что в четырехмерном пространстве (x, y, z, t) это не одна, а много единичных волн, каждая со своим центром излучения (ξc, ηc, ζc) и моментом излучения ԏc. Обратите внимание, что r, rи и ԏ (или ԏc) здесь имеют совсем другой смысл, чем в определении запаздывающих потенциалов. Отметим также, что rи и ξ, η, ζ являются переменными, зависимыми от ԏ:
rи = rи(ԏ), ξ = ξ(ԏ), η = η(ԏ), ζ = ζ(ԏ).
В интернете есть много физических апплетов, в том числе для эффекта Доплера. См. например,
http://www.astro.ubc…ppler.html
http://www.lon-capa.…pler/d.htm
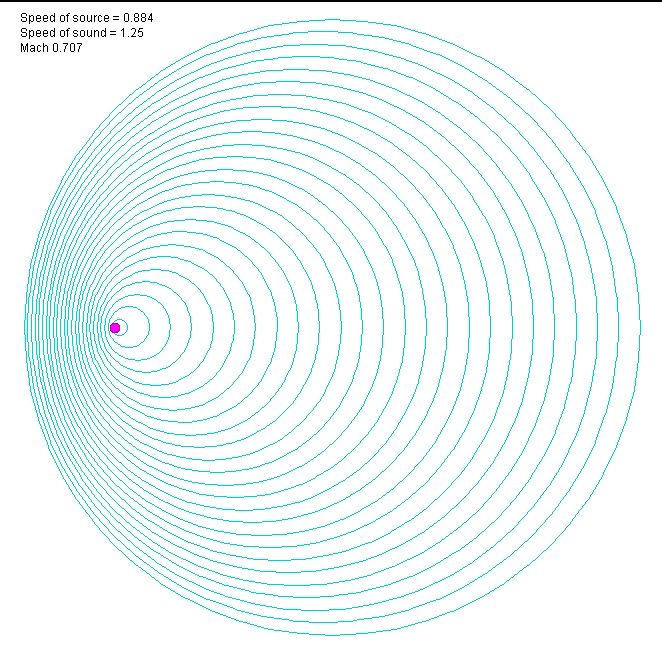
Эти апплеты как раз и показывают распространение волн от источника, движущегося с постоянной скоростью. Ниже показан мгновенный снимок (Print Screen) последовательных волн, распространяющихся от источника со скоростью v = 0.707 c:
Сравнивая уравнение (x – ξ)₂ + (y – η)₂ + (z – ζ)₂ = c₂(t – ԏ)₂ с тем, что написано выше о полной функции y = 3(x – u)₃ + p в четырехмерном пространстве, легко понять, что любая полная функция f, описывающая распространение всех волн от движущегося источника, должна зависеть не только от переменных x, y, z и t, но и от ξ, η, ζ и ԏ. То есть она должна зависеть от 6 пространственных и 2 временных координат, а изображаться, соответственно, в 9-мерном пространстве:
f = f(x, y, z, ξ, η, ζ, t, ԏ)
Полный дифференциал этой полной функции будет равен:
Df = (∂f/∂x)dx + (∂f/∂ξ)dξ + (∂f/∂y)dy + (∂f/∂η)dη + (∂f/∂z)dz + (∂f/∂ζ)dζ + (∂f/∂t)dt + (∂f/∂ԏ)dԏ
Поскольку x и ξ, y и η, z и ζ, t и ԏ всегда встречаются парами: f = f(x - ξ, y - η, z - ζ, t - ԏ), то нетрудно убедиться, что
Df = (∂f/∂x)(dx – dξ) + (∂f/∂y)(dy – dη) + (∂f/∂z)(dz – dζ) + (∂f/∂t)(dt – dԏ)
Если источник движется по прямой линии, то оси координат можно выбрать так, чтобы движение происходило только по оси x, а η и ζ в любой момент времени были равны нулю. Тогда их можно исключить из рассмотрения и остаются только x, y, z, ξ, t, ԏ. Если, далее, источник движется с постоянной скоростью v₀, мы можем выразить ξ через ԏ:
ξ = v₀ԏ
Это, однако, не позволит нам избавиться и от ξ тоже, поскольку ξ остается переменной. Избавиться можно только от тех переменных, которые в любой момент времени равны нулю или константе. Таким образом, минимальное количество пространственных координат для описания источника, движущегося по прямой линии, должно быть 4, а временных координат – 2:
Df(x, y, z, ξ, t, ԏ) = (∂f/∂x)(dx – dξ) + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)(dt – dԏ)
Если же мы не учитываем переменных ξ и ԏ и считаем, что полный дифференциал равен
df = (∂f/∂x)dx + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)dt,
то это не полный дифференциал от полной функции f(x, y, z, ξ, t, ԏ) в семимерном пространстве (x, y, z, ξ, t, ԏ, f), описывающей все волны от источника, испущенные во все моменты времени, а единичный дифференциал в пятимерном пространстве (x, y, z, t, f) только одной единичной волны, испущенной, скажем, в момент t₁ в точке x = x₁, y = 0, z = 0:
df(x, y, z, x₁, t, t₁) = (∂f/∂x)dx + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)dt
Напомню, что эта единичная волна распространяется со скоростью с и в любой момент времени она должна удовлетворять уравнению
(x – x₁)₂ + y₂ + z₂ = c₂(t – t₁)₂
или
r – ix₁ = c(t – t₁),
где i, j, k – единичные векторы по осям x, y, z.
Во всех точках вне этой расширяющейся сферы, единичная функция f(x, y, z, x₁, t, t₁) равна 0. Обозначим |r – ix₁| как r₁, а направляющие косинусы луча волны как cos α, cos β и cos γ. Подчеркнем, что если источник испускает последовательные волны, а не одну-единственную волну, то для любой единичной волны cos α ≠ (x – x₁)/r₁, cos β ≠ y/r₁, cos γ = z/r₁, поскольку лучи волн, как будет показано ниже, искривляются. При распространении волны, cos α, cos β и cos γ все время меняются, они не постоянны.
Заметим, что если в момент времени t единичная волна находится в точке (x, y, z), то в момент t + dt она переместится на расстояние cdt от центра волны – точки с координатами (x₁, 0, 0). При этом, x, y и z изменятся одновременно и пропорционально cdt:
dx = cdt cos α
dy = cdt cos β
dz = cdt cos γ
x₂ + y₂ + z₂ = c₂t₂
Это уравнение, возможно, не столь «научно», как волновое уравнение в частных производных:
∂₂u/∂t₂ – c₂∇₂u = K(x, y, z, t)
Но оно имеет то преимущество, что оно очень наглядно. Будем его использовать как «нулевое приближение», как «контроль на физический смысл», для качественной оценки волновых процессов. С ним труднее сделать ошибки.
Легко увидеть, что уравнение x₂ + y₂ + z₂ = c₂t₂ описывает распространение фронта сферической волны, которая была испущена из точки с координатами (0, 0, 0) в момент времени t = 0. Чем больше t, тем больше сфера с радиусом r = (x₂ + y₂ + z₂)₀.₅ = ct.
Но ведь волны – это не один только импульс в нулевой момент времени, правильно? А как нам описать распространение волны, испущенной в момент t₁? А мы только что разбирали похожий пример – как:
x₂ + y₂ + z₂ = c₂(t – t₁)₂
Подчеркнем, что это – другая волна, другая единичная функция, если мы пользуемся только четырехмерным пространством (x, y, z, t).
Теперь предположим, что источник движется с произвольной скоростью v в произвольном направлении и излучает волны, одну за другой. Как мы можем описать это семейство волн? Распространение каждой волны, испущенной в точке с координатами (ξ, η, ζ) в момент времени ԏ, будет удовлетворять следующему уравнению:
(x – ξ)₂ + (y – η)₂ + (z – ζ)₂ = c₂(t – ԏ)₂
или
r – rи = c(t – ԏ),
где r – это радиус-вектор (из начала координат) какой-либо точки распространяющейся волны в момент t, rи – радиус-вектор источника волн в момент ԏ.
Подчеркнем, что в четырехмерном пространстве (x, y, z, t) это не одна, а много единичных волн, каждая со своим центром излучения (ξc, ηc, ζc) и моментом излучения ԏc. Обратите внимание, что r, rи и ԏ (или ԏc) здесь имеют совсем другой смысл, чем в определении запаздывающих потенциалов. Отметим также, что rи и ξ, η, ζ являются переменными, зависимыми от ԏ:
rи = rи(ԏ), ξ = ξ(ԏ), η = η(ԏ), ζ = ζ(ԏ).
В интернете есть много физических апплетов, в том числе для эффекта Доплера. См. например,
http://www.astro.ubc…ppler.html
http://www.lon-capa.…pler/d.htm
Эти апплеты как раз и показывают распространение волн от источника, движущегося с постоянной скоростью. Ниже показан мгновенный снимок (Print Screen) последовательных волн, распространяющихся от источника со скоростью v = 0.707 c:

Сравнивая уравнение (x – ξ)₂ + (y – η)₂ + (z – ζ)₂ = c₂(t – ԏ)₂ с тем, что написано выше о полной функции y = 3(x – u)₃ + p в четырехмерном пространстве, легко понять, что любая полная функция f, описывающая распространение всех волн от движущегося источника, должна зависеть не только от переменных x, y, z и t, но и от ξ, η, ζ и ԏ. То есть она должна зависеть от 6 пространственных и 2 временных координат, а изображаться, соответственно, в 9-мерном пространстве:
f = f(x, y, z, ξ, η, ζ, t, ԏ)
Полный дифференциал этой полной функции будет равен:
Df = (∂f/∂x)dx + (∂f/∂ξ)dξ + (∂f/∂y)dy + (∂f/∂η)dη + (∂f/∂z)dz + (∂f/∂ζ)dζ + (∂f/∂t)dt + (∂f/∂ԏ)dԏ
Поскольку x и ξ, y и η, z и ζ, t и ԏ всегда встречаются парами: f = f(x - ξ, y - η, z - ζ, t - ԏ), то нетрудно убедиться, что
Df = (∂f/∂x)(dx – dξ) + (∂f/∂y)(dy – dη) + (∂f/∂z)(dz – dζ) + (∂f/∂t)(dt – dԏ)
Если источник движется по прямой линии, то оси координат можно выбрать так, чтобы движение происходило только по оси x, а η и ζ в любой момент времени были равны нулю. Тогда их можно исключить из рассмотрения и остаются только x, y, z, ξ, t, ԏ. Если, далее, источник движется с постоянной скоростью v₀, мы можем выразить ξ через ԏ:
ξ = v₀ԏ
Это, однако, не позволит нам избавиться и от ξ тоже, поскольку ξ остается переменной. Избавиться можно только от тех переменных, которые в любой момент времени равны нулю или константе. Таким образом, минимальное количество пространственных координат для описания источника, движущегося по прямой линии, должно быть 4, а временных координат – 2:
Df(x, y, z, ξ, t, ԏ) = (∂f/∂x)(dx – dξ) + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)(dt – dԏ)
Если же мы не учитываем переменных ξ и ԏ и считаем, что полный дифференциал равен
df = (∂f/∂x)dx + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)dt,
то это не полный дифференциал от полной функции f(x, y, z, ξ, t, ԏ) в семимерном пространстве (x, y, z, ξ, t, ԏ, f), описывающей все волны от источника, испущенные во все моменты времени, а единичный дифференциал в пятимерном пространстве (x, y, z, t, f) только одной единичной волны, испущенной, скажем, в момент t₁ в точке x = x₁, y = 0, z = 0:
df(x, y, z, x₁, t, t₁) = (∂f/∂x)dx + (∂f/∂y)dy + (∂f/∂z)dz + (∂f/∂t)dt
Напомню, что эта единичная волна распространяется со скоростью с и в любой момент времени она должна удовлетворять уравнению
(x – x₁)₂ + y₂ + z₂ = c₂(t – t₁)₂
или
r – ix₁ = c(t – t₁),
где i, j, k – единичные векторы по осям x, y, z.
Во всех точках вне этой расширяющейся сферы, единичная функция f(x, y, z, x₁, t, t₁) равна 0. Обозначим |r – ix₁| как r₁, а направляющие косинусы луча волны как cos α, cos β и cos γ. Подчеркнем, что если источник испускает последовательные волны, а не одну-единственную волну, то для любой единичной волны cos α ≠ (x – x₁)/r₁, cos β ≠ y/r₁, cos γ = z/r₁, поскольку лучи волн, как будет показано ниже, искривляются. При распространении волны, cos α, cos β и cos γ все время меняются, они не постоянны.
Заметим, что если в момент времени t единичная волна находится в точке (x, y, z), то в момент t + dt она переместится на расстояние cdt от центра волны – точки с координатами (x₁, 0, 0). При этом, x, y и z изменятся одновременно и пропорционально cdt:
dx = cdt cos α
dy = cdt cos β
dz = cdt cos γ
Отредактировано: Yuri Rus - 21 ноя 2019 00:20:27

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Я думаю, теперь легко понять, почему ранее упомянутый аргумент из книги Leigh Page ”Introduction to Theoretical Physics” неверен. Приведу эту цитату еще раз:


(я с удовольствием заменю это на русский текст, если мне дадут ссылку на подходящую книгу)
Здесь, на самом деле, много ошибок (прежде всего, в уравнении полностью отсутствует источник и какой-либо намек на его движение), но я их касаться сейчас не буду . Позже я именно об этом буду много говорить. Главным для меня сейчас является вот такой аргумент:
Если электрический заряд двигается по оси х, напряженность электрического поля Е в точке (x + vdt, y, z) в момент времени t + dt должна быть такой же, как в точке (x, y, z) в момент t, то есть
E(x + vdt, y, z, t + dt) = E(x, y, z, t)
В то же время, левый член, в соответствии с принятым в физике определением полного дифференциала (не моим определением, разумеется) можно разложить на
E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt
Отсюда получается
∂E/∂t = – v (∂E/∂x)
Повторив эту математическую манипуляцию еще раз, получаем
∂₂E/∂t₂ = v₂ (∂₂E/∂x₂)
а также
(1 – β₂)(∂₂E/∂x₂) + ∂₂E/∂y₂ + ∂₂E/∂z₂ = 0
Я даже не буду останавливаться на том, что после этих математических манипуляций трехмерное волновое уравнение со скоростью распространения волн c трансформировалось в одномерное волновое уравнение со скоростью распространения волн v и в уравнение Лапласа со «сплющенной» координатой х, что не имеет никакого физического смысла. Меня здесь интересует только это уравнение:
E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt
Предположительно, это уравнение следует из определения «классического» полного дифференциала:
dE = (∂E/∂x)dx + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)dt
Полагая dx = vdt, dy = 0, dz = 0, dt = dt, автор и получил вышеприведенное уравнение.
Однако мы же теперь вооружены всесильным, потому что верным, определением полного дифференциала DЕ как:
DE(x, y, z, ξ, t, ԏ) = (∂E/∂x)(dx – dξ) + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)(dt – dԏ)
Благодаря этому определению, мы сразу видим, что вместо E(x, y, z, t) и E(x + vdt, y, z, t + dt) следует использовать E(x, y, z, ξ, t, ԏ) и E(x + vdt, y, z, ξ + vdt, t + dt, ԏ + dt). Необходимо, таким образом, учитывать не только dx = vdt, dy = 0, dz = 0, dt = dt, но и dξ = vdt и dԏ = dt. И поскольку dx = dξ и dt = dԏ (а также dy = 0, dz = 0), то при переходе от точки (x, y, z, ξ, t, ԏ) к точке (x + vdt, y, z, ξ + vdt, t + dt, ԏ + dt), как (∂E/∂x)(dx – dξ), так и (∂E/∂t)(dt – dԏ) равны 0. Никакого равенства
∂E/∂t = – v (∂E/∂x)
нет, а следовательно, нет и никакого сжатия по оси х.
В рамках предлагаемой теории, «классический» полный дифференциал на самом деле является всего лишь единичным дифференциалом. Он имеет смысл только для фиксированных значений ξ и ԏ:
dE(x, y, z, ξс, t, ԏс) = (∂E/∂x)dx + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)dt ,
то есть только для единичной волны, испущенной в точке (ξс, 0, 0) в момент времени ԏс. Как уже говорилось выше, при увеличении t на dt, волна эта перемещается на расстояние cdt, причем x, y и z изменятся одновременно и пропорционально скорости распространения волны c (а не скорости источника v):
dx = cdt cos α
dy = cdt cos β
dz = cdt cos γ
Таким образом, в момент t + dt эта единичная волна из точки (x, y, z) сместится в точку
(x + cdt cos α, y + cdt cos β, z + cdt cos γ).
Что касается E(x, y, z, t) и E(x + vdt, y, z, t + dt), то очевидно, что они принадлежат разным единичным волнам, разным единичным функциям. Уравнение же
E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt
не имеет ни физического, ни математического смысла.
Я уделил так много внимания этому уравнению, потому что в нем в наиболее ясной и простой форме выражена типичная ошибка математической физики: полный дифференциал не включает частных производных по координатам движущегося источника как независимым переменным, и вообще движение источника никак не отражается в волновом уравнении. Кроме того, вышеприведенный аргумент с выведением
(1 – β₂)(∂₂E/∂x₂) + ∂₂E/∂y₂ + ∂₂E/∂z₂ = 0
исторически сыграл важную роль в признании преобразований Лоренца и теории относительности, поскольку здесь в рамках вроде бы совершенно классической электродинамики и векторного анализа получается «сжатие» поля частицы в направлении ее движения. Я хотел показать, что этот аргумент неверен – вследствие неверного понимания, что такое полный дифференциал функции.
Далее, очевидно, что полная функция f(x, y, z, ξ, η, ζ, t, ԏ) будет описывать волны только от одного движущегося источника. Если источников два, то взаимодействующие волны от этих источников потребуют введения не 4-х дополнительных координат ξ, η, ζ, ԏ, но 8-ми координат: ξ₁, η₁, ζ₁, ԏ₁, ξ₂, η₂, ζ₂, ԏ₂. Для n движущихся источников, потребуются уже 4n дополнительных координат: ξ₁, η₁, ζ₁, ԏ₁, ξ₂, η₂, ζ₂, ԏ₂ … ξn, ηn, ζn, ԏn. Аналогично изменится и полный дифференциал этой полной функции. Позже мы вернемся к этому вопросу. в частности, пересмотрим основные положения векторного анализа.


(я с удовольствием заменю это на русский текст, если мне дадут ссылку на подходящую книгу)
Здесь, на самом деле, много ошибок (прежде всего, в уравнении полностью отсутствует источник и какой-либо намек на его движение), но я их касаться сейчас не буду . Позже я именно об этом буду много говорить. Главным для меня сейчас является вот такой аргумент:
Если электрический заряд двигается по оси х, напряженность электрического поля Е в точке (x + vdt, y, z) в момент времени t + dt должна быть такой же, как в точке (x, y, z) в момент t, то есть
E(x + vdt, y, z, t + dt) = E(x, y, z, t)
В то же время, левый член, в соответствии с принятым в физике определением полного дифференциала (не моим определением, разумеется) можно разложить на
E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt
Отсюда получается
∂E/∂t = – v (∂E/∂x)
Повторив эту математическую манипуляцию еще раз, получаем
∂₂E/∂t₂ = v₂ (∂₂E/∂x₂)
а также
(1 – β₂)(∂₂E/∂x₂) + ∂₂E/∂y₂ + ∂₂E/∂z₂ = 0
Я даже не буду останавливаться на том, что после этих математических манипуляций трехмерное волновое уравнение со скоростью распространения волн c трансформировалось в одномерное волновое уравнение со скоростью распространения волн v и в уравнение Лапласа со «сплющенной» координатой х, что не имеет никакого физического смысла. Меня здесь интересует только это уравнение:
E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt
Предположительно, это уравнение следует из определения «классического» полного дифференциала:
dE = (∂E/∂x)dx + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)dt
Полагая dx = vdt, dy = 0, dz = 0, dt = dt, автор и получил вышеприведенное уравнение.
Однако мы же теперь вооружены всесильным, потому что верным, определением полного дифференциала DЕ как:
DE(x, y, z, ξ, t, ԏ) = (∂E/∂x)(dx – dξ) + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)(dt – dԏ)
Благодаря этому определению, мы сразу видим, что вместо E(x, y, z, t) и E(x + vdt, y, z, t + dt) следует использовать E(x, y, z, ξ, t, ԏ) и E(x + vdt, y, z, ξ + vdt, t + dt, ԏ + dt). Необходимо, таким образом, учитывать не только dx = vdt, dy = 0, dz = 0, dt = dt, но и dξ = vdt и dԏ = dt. И поскольку dx = dξ и dt = dԏ (а также dy = 0, dz = 0), то при переходе от точки (x, y, z, ξ, t, ԏ) к точке (x + vdt, y, z, ξ + vdt, t + dt, ԏ + dt), как (∂E/∂x)(dx – dξ), так и (∂E/∂t)(dt – dԏ) равны 0. Никакого равенства
∂E/∂t = – v (∂E/∂x)
нет, а следовательно, нет и никакого сжатия по оси х.
В рамках предлагаемой теории, «классический» полный дифференциал на самом деле является всего лишь единичным дифференциалом. Он имеет смысл только для фиксированных значений ξ и ԏ:
dE(x, y, z, ξс, t, ԏс) = (∂E/∂x)dx + (∂E/∂y)dy + (∂E/∂z)dz + (∂E/∂t)dt ,
то есть только для единичной волны, испущенной в точке (ξс, 0, 0) в момент времени ԏс. Как уже говорилось выше, при увеличении t на dt, волна эта перемещается на расстояние cdt, причем x, y и z изменятся одновременно и пропорционально скорости распространения волны c (а не скорости источника v):
dx = cdt cos α
dy = cdt cos β
dz = cdt cos γ
Таким образом, в момент t + dt эта единичная волна из точки (x, y, z) сместится в точку
(x + cdt cos α, y + cdt cos β, z + cdt cos γ).
Что касается E(x, y, z, t) и E(x + vdt, y, z, t + dt), то очевидно, что они принадлежат разным единичным волнам, разным единичным функциям. Уравнение же
E(x + vdt, y, z, t + dt) = E(x, y, z, t) + (∂E/∂x)vdt + (∂E/∂t)dt
не имеет ни физического, ни математического смысла.
Я уделил так много внимания этому уравнению, потому что в нем в наиболее ясной и простой форме выражена типичная ошибка математической физики: полный дифференциал не включает частных производных по координатам движущегося источника как независимым переменным, и вообще движение источника никак не отражается в волновом уравнении. Кроме того, вышеприведенный аргумент с выведением
(1 – β₂)(∂₂E/∂x₂) + ∂₂E/∂y₂ + ∂₂E/∂z₂ = 0
исторически сыграл важную роль в признании преобразований Лоренца и теории относительности, поскольку здесь в рамках вроде бы совершенно классической электродинамики и векторного анализа получается «сжатие» поля частицы в направлении ее движения. Я хотел показать, что этот аргумент неверен – вследствие неверного понимания, что такое полный дифференциал функции.
Далее, очевидно, что полная функция f(x, y, z, ξ, η, ζ, t, ԏ) будет описывать волны только от одного движущегося источника. Если источников два, то взаимодействующие волны от этих источников потребуют введения не 4-х дополнительных координат ξ, η, ζ, ԏ, но 8-ми координат: ξ₁, η₁, ζ₁, ԏ₁, ξ₂, η₂, ζ₂, ԏ₂. Для n движущихся источников, потребуются уже 4n дополнительных координат: ξ₁, η₁, ζ₁, ԏ₁, ξ₂, η₂, ζ₂, ԏ₂ … ξn, ηn, ζn, ԏn. Аналогично изменится и полный дифференциал этой полной функции. Позже мы вернемся к этому вопросу. в частности, пересмотрим основные положения векторного анализа.
Отредактировано: Yuri Rus - 21 ноя 2019 00:23:28

Москва
Карма: +1.82
Регистрация: 20.03.2009
Сообщений: 59
Читатели: 0
Регистрация: 20.03.2009
Сообщений: 59
Читатели: 0
С почином вас.
И с праздником, конечно.
Отличное начало! В первых своих выкладках вами (наряду с многими другими) очередной раз показана абсурдность независимости "с" от скорости источника по мнению этого источника и доказана возможность однозначного определения наличия равномерного движения железнодорожного вагона ) патентным поверенным, сидящим внутри него. :)
Также радует развенчание притянутого (за уши) - вслед за этой высосанной из пальца парочкой - принципа "относительности одновременности".
Поздравляю, спасибо, ждем продолжения.
И с праздником, конечно.
Отличное начало! В первых своих выкладках вами (наряду с многими другими) очередной раз показана абсурдность независимости "с" от скорости источника по мнению этого источника и доказана возможность однозначного определения наличия равномерного движения железнодорожного вагона ) патентным поверенным, сидящим внутри него. :)
Также радует развенчание притянутого (за уши) - вслед за этой высосанной из пальца парочкой - принципа "относительности одновременности".
Поздравляю, спасибо, ждем продолжения.
Не скрою. Удивлён..

64 года
Карма: +395.63
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,394
Читатели: 1
Модератор ветки
Цитата: TIR от 12.04.2011 23:12:50
С почином вас.
И с праздником, конечно.
Отличное начало! В первых своих выкладках вами (наряду с многими другими) очередной раз показана абсурдность независимости "с" от скорости источника по мнению этого источника и доказана возможность однозначного определения наличия равномерного движения железнодорожного вагона ) патентным поверенным, сидящим внутри него. :)
Также радует развенчание притянутого (за уши) - вслед за этой высосанной из пальца парочкой - принципа "относительности одновременности".
Поздравляю, спасибо, ждем продолжения.
Спасибо за положительный отзыв. Но вообще-то Вы опережаете события - об абсурдности независимости с от скорости источника по мнению этого источника, возможности однозначного определения наличия равномерного движения железнодорожного вагона патентным поверенным, сидящим внутри него. и развенчании принципа "относительности одновременности" я пока не говорил. Буду говорить, когда речь зайдет об искривлении силовых линий и траекторий лучей.
Теория относительности вообще не является моей главной мишенью. Является - вся физика. О ТО я вынужден буду говорить (и уже немного говорил), но она неверна не сама по себе, а потому, что неверна почти вся классическая механика. Мат. аппарат физики - неверен.
Сейчас на ветке:
1,
Модераторов: 0,
Пользователей: 0,
Гостей: 0,
Ботов: 1