Жизнь, Разум, Человек, Религия и Наука

Цитата: Yuri Rus от 12.04.2011 10:31:01
Я думаю, теперь легко понять, почему ранее упомянутый аргумент из книги Leigh Page ”Introduction to Theoretical Physics” неверен.
<skip>

Я уделил так много внимания этому уравнению, потому что в нем в наиболее ясной и простой форме выражена типичная ошибка математической физики: полный дифференциал не включает частных производных по координатам движущегося источника как независимым переменным, и вообще движение источника никак не отражается в волновом уравнении.

Подход несомненно интересный, и уже  с нетерпением жду продолжения.
Однако физика  данного противопоставления осталась неясной.
В приведенном  тексте на английском речь идет о статическом электрическом поле, хотя и с движущимся источником ( зарядом ).
Вы же рассматриваете поле f скорее как мгновенное излучение источником некоторой сферической волны.
Конечно, в  физике давно уже практически отождествились статическое поле и  электромагнитное излучение в концепции фотонов, но это так сказать в другой "квантовой" модели.
Здесь же рассматривается вполне классическое "дифференциальное" описание, в рамках которого статическое поле и излучениие принято ( было ? ) различать.
Вот кстати уже не совсем свежий пример:

Цитата: hedin от 15.02.2011 23:40:00
<skip>
PS И, в общем-то, постоянное магнитное поле - это не излучение. Это поле, статическое.

Готов согласиться, что на самом деле нет никаких физических способов различить статическое электрическое поле от постоянно пробегающих волн. Грубая аналогия - тащат щепку к берегу с постоянной силой за невидимую леску, или эту щепку прибивает к берегу равномерной мелкой волной, по движению самой щепки ( нашего пробного тела ) не различить.

Но как я уже показал, физики пока  статику и излучение ( волну ) как-то  различают. Конечно при этом забавно наблюдать как они же и выводят волновое уравнение из статики.

Цитата: Поверонов от 13.04.2011 00:07:31Подход несомненно интересный, и уже  с нетерпением жду продолжения.
Однако физика  данного противопоставления осталась неясной.
В приведенном  тексте на английском речь идет о статическом электрическом поле, хотя и с движущимся источником ( зарядом ).
Вы же рассматриваете поле f скорее как мгновенное излучение источником некоторой сферической волны.
Конечно, в  физике давно уже практически отождествились статическое поле и  электромагнитное излучение в концепции фотонов, но это так сказать в другой "квантовой" модели.
Здесь же рассматривается вполне классическое "дифференциальное" описание, в рамках которого статическое поле и излучениие принято ( было ? ) различать.
Вот кстати уже не совсем свежий пример:

Готов согласиться, что на самом деле нет никаких физических способов различить статическое электрическое поле от постоянно пробегающих волн. Грубая аналогия - тащат щепку к берегу с постоянной силой за невидимую леску, или эту щепку прибивает к берегу равномерной мелкой волной, по движению самой щепки ( нашего пробного тела ) не различить.

Но как я уже показал, физики пока  статику и излучение ( волну ) как-то  различают. Конечно при этом забавно наблюдать как они же и выводят волновое уравнение из статики.

Ув. Поверонов, во-первых, в цитированном тексте Leigh Page речь идет НЕ о статическом электрическом поле, а об электромагнитных волнах. Я не показывал, как там было выведено волновое уравнение (156-2) для Е. Вот так:
 


 
Обратите внимание на фразу (в переводе на русский):

Это уравнения волны, распространяющейся с фазовой скоростью
 

 
Именно благодаря тому, что Максвелл получил волновые уравнения для E и B и предсказал существование электромагнитных волн, его теория и была признана научным сообществом. Можно сказать, это самое главное в теории Максвелла.

Во-вторых, о какой статике может идти речь, если заряд движется? Если Вы посмотрите книгу Фейнман Р., Лейтон Р., Сэндс М. «Фейнмановские Лекции по Физике», т. 6 «Электродинамика», гл. 21, § 2, то увидите, что потенциалы  φ  и  А  определяются волновыми уравнениями
 

 
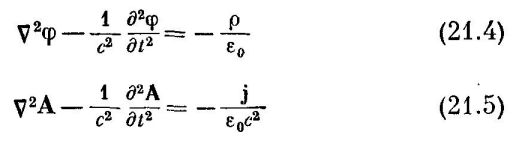
Далее в той же главе 21, в § 6 "Потенциалы заряда, движущегося с ростоянной скоростью; формула Лоренца", преобразования Лоренца выводятся именно из запаздывания потенциалов, распространяющихся как волны со скоростью с:
 



 
Пардон за такие длинные цитаты. Я хотел подчеркнуть, что волны, распространяющиеся со скоростью света с от движущегося заряда, играют фундаментальную, ключевую роль в электродинамике - как в теории Максвелла, так и в теории относительности.

Это совершенно не значит, что я согласен с любой из этих теорий. Я просто отвечаю на Ваш вопрос о различении между статикой и излучением в физике, и пытаюсь показать, что в данном случае - электродинамика однозначно выбирает излучение.

Цитата: Yuri Rus от 13.04.2011 04:14:45
Ув. Поверонов, во-первых, в цитированном тексте Leigh Page речь идет НЕ о статическом электрическом поле, а об электромагнитных волнах. Я не показывал, как там было выведено волновое уравнение (156-2) для Е. Вот так:

<skip>

Собственно подозрение о статичности поля  в рассматриваемом отрывке возникло из следующего абзаца

Цитата: Yuri Rus от 12.04.2011 10:31:01
If the charge is located at the origin at the instant considered, the boundary conditions of the problem are: (1) the electric flux through any small surface surrounding the origin, or the number of tubes of electric force devergng from the origin, must equal e, (2) the electric intensity must vanish at infinity.
Take the X axis in the direction of motion. As its field moves with the charge the electric intensity at the point x + v dt, y, z at the time t + dt must be the same as at x, y, z at the time t, that is,
                   E(x + v dt, y, z, t + dt) = E ( x, y, z, t )

в котором фактически и постулируется  статичность поля, которое заряд как бы "тащит за собой".  Но если Вы уверены, что в отрывке и у них  речь идет об излучении, то тем более нет проблем. Ждем продолжения.

Цитата: Поверонов от 14.04.2011 01:43:30
Собственно подозрение о статичности поля  в рассматриваемом отрывке возникло из следующего абзаца

в котором фактически и постулируется  статичность поля, которое заряд как бы "тащит за собой".  Но если Вы уверены, что в отрывке и у них  речь идет об излучении, то тем более нет проблем. Ждем продолжения.

Понимаете, Ваш вопрос о статичности поля хороший и правильный, он безусловно имеет смысл. Но он очень преждевременный - мне пришлось бы залезть слишком далеко вперед. Поэтому я сейчас уклоняюсь от ответа на него и ссылаюсь на то, что в разбираемом вопросе в рамках теории Максвелла и ТО речь идет о бегущих волнах.

Позже к нему безусловно имеет смысл вернуться - когда мы будем говорить о том, что же такое Кулоновское поле, какой его физический смысл (излучение ли волн, смещение ли частиц светопроводящей среды, и т.д.). Я буду стараться показать, что существует только одно физическое поле, а все известные физике силы являются его проявлениями при движении заряженных частиц. Закон Кулона, как я утверждаю, неверен, он приблизителен - на самом деле, это поле имеет знакопеременный характер. Знакопеременность означает, что никакого сильного и слабого взаимодействий вообще нет, это ошибочная интерпретация экспериментальных данных.  Но до этого еще дойти надо.

Цитата: problemsolver
То есть, я правильно понимаю, что мы присутствуем при описании всеобщей теории поля?

Из Ваших слов, можно предположить, что Вы разделяете отношение к единой теории поля как к Священному Граалю, завершающему величественное здание физики. Вместо такого завершения, я утверждаю, что почти все здание физики построено на ложном математическом фундаменте. Всё нужно ломать и строить совершенно другое здание физики. С нуля.

При этом, сам я занимаюсь только фундаментом, а не верхними этажами. Построить все здание заново - задача, непосильная для меня одного. Моя цель - показать, что фундамент фальшив, положить несколько первых камешков, и надеяться, что другие меня поймут и продолжат построение здания новой науки.

Думаю, если я смогу продемонстрировать некоторые практические следствия моей теории - например, искусственную гравитацию, - тогда других доказательств не понадобится. Но на самом деле, и помимо искусственной гравитации, из моей теории следует множество легко проверяемых следствий, которые, я надеюсь, убедят кого-то из физиков или людей, интересующихся физикой, в том, что "старая" физика неверна, и они продолжат мою работу. Ну, а не убедят - придется все-таки создавать генератор искусственной гравитации. Это не так уж сложно, если знаешь, как.

Чтобы освежить в памяти читателей вывод «классического» волнового уравнения в частных производных, приведу цитаты из учебника Кошляков Н.С., Глинер Э.Б., Смирнов М.М. «Уравнения в частных производных математической физики» (1970). Здесь это расписано довольно подробно, в отличие от многих других учебников, где внешняя сила часто вообще не упоминается и можно понять так, что однородное волновое уравнение способно описать любые волны, включая волны от источников. Текста много, все читать не обязательно, тем более тем, кто это помнит. Я буду ссылаться на определенные разделы в дальнейшем, так чтобы было под рукой. Поскольку цитат ну очень много, я выделил синим цветом мои комментарии, чтобы легче было отличить их от цитат.


Уравнение колебаний струны, стр. 12-15:
 





 
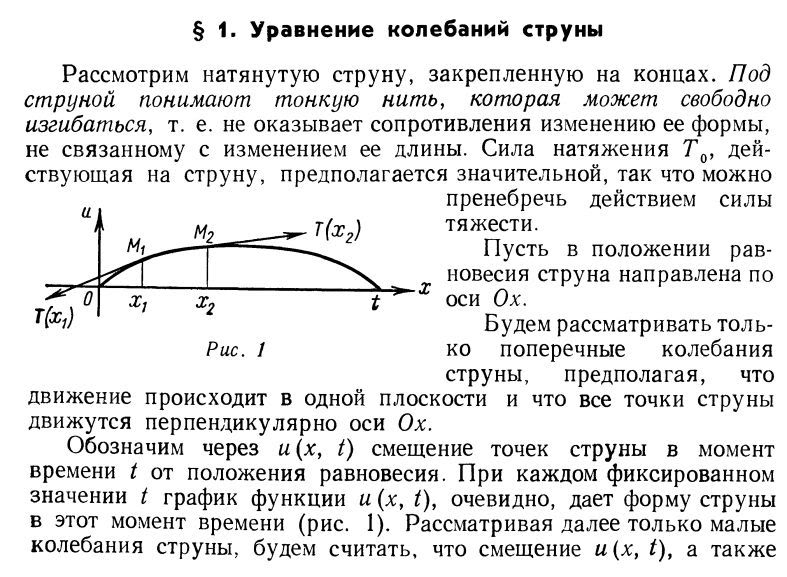
Решение Д'Аламбера этого уравнения, стр. 54-55:
 


 
Уравнения гидродинамики и звуковых волн, стр. 18-24:
 







  
Формула Пуассона, стр. 98-101:
 




 
Неоднородное волновое уравнение и запаздывающие потенциалы, стр. 105-109:
 





 
Приведу также цитаты из книги Курант Р., Гильберт Д. «Методы математической физики», т. 2 (1945).

Задача Коши для волнового уравнения, стр. 182-183:
 


 
Неоднородное волновое уравнение и запаздывающие потенциалы, стр. 187-191:
 





 
Проблема излучения, процессы распространения и принцип Гюйгенса, стр. 191-194:
 





 
На что здесь следует обратить внимание?
 
1. Весь анализ, все уравнения относятся к некому элементу среды, расположенному в произвольном месте. Не к источнику, который находится в совершенно другом месте и может двигаться, менять свою интенсивность произвольным образом, что угодно, а к элементу среды, находящемуся на некотором расстоянии от источника.

Если внешняя сила равна нулю, то есть в отсутствие источников волн, однородное волновое уравнение 

∂²u/∂t² – c²∂²u/∂x² = 0   или   ∂²u/∂t² – c²∇²u = 0 

описывает свободные колебания среды. Эти колебания, действительно, распространяются со скоростью  с, как единое целое, и для них выполняется принцип суперпозиции.

В случае однородного волнового уравнения, начальные условия принципиально не могут описать источник, который генерирует последовательные волны на протяжении какого-то периода времени. Начальные условия, по определению, могут описать лишь мгновенную деформацию, дислокацию, флуктуацию, пусть сколь угодно протяженную, пусть знакопеременную, пусть синусоидную, какую угодно, которая затем распространяется в пространстве и во времени. Это – не волны от источника, тем более движущегося.

В случае однородного волнового уравнения, граничные условия могут описать неподвижный источник волн (для струны, но не в трехмерном случае), но не движущийся.

Суммируя вышесказанное, подчеркнем, что так называемое однородное волновое уравнение вообще не следует называть волновым, потому что оно описывает только свободные колебания среды, а не волны от источника. Это уравнение свободных колебаний – так его и следует называть, чтобы не возникало путаницы с неоднородным волновым уравнением (неоднородным, потому что внешняя сила не равна нулю). «Настоящие» волны должны иметь источник.

2. Ключевую роль при выводе волнового уравнения играет принцип Д’Аламбера, согласно которому все силы, действующие на некий элемент среды, включая силу инерции, должны уравновешиваться. По сути, принцип Д’Аламбера – это не что иное, как Второй Закон Ньютона. Можно даже сказать, что волновое уравнение - это другая форма записи Второго Закона Ньютона. Именно в этом заключается его физический смысл. Да, волновое уравнение можно получить и другими способами (например, используя принцип Гамильтона), но это не отменяет тот факт, что оно эквивалентно Второму Закону.

3. В случае неоднородного волнового уравнения, где есть внешняя сила  F(x, y, z, t), эта сила действует непосредственно на сам элемент среды.  Если источник волн находится на каком-то расстоянии от данного элемента среды, скажем, в точке  Q(ξ, η, ζ), то сила  F(x, y, z, t)  для этого элемента равна нулю (согласно мат. физике). Сила  F(x, y, z, t) равна нулю везде, кроме той точки (или точек), где находится источник, то есть во всем остальном пространстве следует использовать однородное волновое уравнение. Казалось бы, в этом есть смысл: например, если мы рассматриваем световые волны от сверхновой звезды, которая взорвалась на расстоянии миллион световых лет от Земли, то очевидно, что интенсивность внешней силы в месте расположения источника была (миллион лет назад) во много раз больше, чем в настоящее время в месте расположении элемента светопроводящей среды на Земле.

Примеров такой логики в учебниках или статьях множество – хотя бы в цитированной выше книге Leigh Page (который, кстати, не с дуба упал – именно он в 1912 г. показал, что магнитное поле является релятивистским эффектом движения электрического заряда). Приведу лишь одну цитату из лекций не менее уважаемого Ричарда Фейнмана – Фейнман Р., Лейтон Р., Сэндс М. «Фейнмановские Лекции по Физике», т. 6 «Электродинамика» (1966), гл. 20, § 1:
 


 
Волновое уравнение с движущимся источником иногда записывается в несколько более сложной форме – см. Голдстейн М.Е. «Аэроакустика» (1981), стр. 52:
 

 
Здесь  ԏ – время, относящееся к излучению звуковой волны;  y – координаты источника;  δ(x) – δ-функция Дирака.

Очевидно, что использование  δ-функции имеет абсолютно тот же смысл: сила, с которой источник действует на среду, равна нулю везде, кроме той точки, где находится источник.

Итак, ситуация следующая. Где-то далеко есть источник, который двигается и непрерывно излучает волны. Эти волны, когда они доходят до интересующего нас элемента среды, действуют на него с определенной силой – но уравнения математической физики приравнивают эту силу нулю везде, кроме той точки, где находится (точнее, находился) источник. Волновое уравнение по сути является неоднородным только в этой точке, а во всем остальном пространстве, предлагается пользоваться однородным волновым уравнением, которое, как написано выше в пункте 1, способно описать лишь свободные, но не вынужденные, колебания среды.

4. Формула Пуассона, являющаяся решением трехмерного однородного уравнения 
∂²u/∂t² – c²∇²u = 0,  полностью аналогична решению Д’Аламбера одномерного однородного уравнения   ∂²u/∂t² – c² ∂²u/∂x² = 0.  Оба эти уравнения имеют следующий смысл: в начальный момент времени задается какая-то первоначальная мгновенная деформация или дислокация среды, которая затем распространяется в пространстве и во времени как единое целое, с постоянной скоростью  с.  В случае формулы Пуассона, лучи этой волны являются прямолинейными траекториями. 

Неоднородное волновое уравнение отличается от однородного тем, что деформация среды, создаваемая источником, более не является мгновенной, единичной. Источник, во-первых, локализован в определенном месте, причем он может двигаться. Во-вторых, он действует на протяжении длительного времени, генерируя новые и новые волны.

В первой половине XIX века, французский математик Жан-Мари Констан Дюамель предложил решение неоднородного волнового уравнения путем его сведения к известному решению однородного волнового уравнения, то есть к формуле Пуассона. Аналогично формуле Пуассона, лучи волн от источника, как предполагалось, тоже должны были распространяться по прямым линиям (как следствие принципа суперпозиции). Единственная разница с формулой Пуассона – время теперь стало выражаться с запаздыванием.

Я хочу показать, что это решение неоднородного волнового уравнения является не просто ошибочным. Эта ошибка фундаментальна настолько, что почти все последующее развитие физики было ложным. Дело в том, что волновое уравнение лежит в основе большинства разделов физики (аналогичные ошибки при решении других основных дифференциальных уравнений физики затрагивают остальные ее разделы). Самое главное – волновое уравнение лежит в основе теории электричества и магнетизма. Неправильное решение волнового уравнение, непонимание волновых процессов привели к тому, что практически всё, что написано в учебниках об электричестве и магнетизме, – неверно. Разумеется, тем более неверны теория относительности и квантовая механика. Все это нужно переписывать.

Но мы не можем сразу браться сейчас за электромагнетизм. Сначала нам необходимо разобраться с волновым уравнением. Только тогда, когда мы поймем, что происходит при распространении волн, мы сможем приступить к электромагнетизму. Нам нужно будет пересмотреть и теорию, и заново интерпретировать старые, давно известные экспериментальные факты, касающиеся электричества, магнетизма, оптики и акустики. При этом, что важно, мы получим множество сравнительно легко проверяемых следствий теории, новых эффектов, которые противоречат старой физике и не могут быть объяснены в ее рамках. Так что критерий фальсифицируемости, безусловно, выполнен.

Вопрос не нов.
Л. А. Молотков. О распространении упругих волн от неравномерно движущегося источника. МИАН СССР 1967 г.
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=tm&paperid=2858&option_lang=rus
(Для прохождения по ссылке её надо скопировать и вставить в окно браузера).

Хочется задать два простых вопроса...
Но перед этим замечу вот что. Пытаюсь проникнуть мыслью внутрь тех противоречий, что тут описываются, и, по правде говоря, не очень удается. Вообще трудности для понимания вызывает вот какая вещь, если мы считаем, что математический аппарат, он же фундамент физики, в нашей дискуссии, неверен, то отчего же он позволяет предсказать результаты эксперимента с приемлемой точностью? Ведь критерием удовлетворительности любой теории является соответствие предсказываемых ею результатов с экспериментальными данными. Я позволю себе напомнить, что чаще всего в физике сначала появляется идея, а уж затем математический аппарат, ее описывающий. Здесь же, нам предлагается пойти обратным путем, сначала решить уравнения, а из них вывести теорию. Более того, физика - это всегда упрощение, а отнюдь не усложнение. Все физические теории, все до единой, являются некой абстракцией, моделью, грубо описывающей реальность. Все эти теории по определению есть приближение к реальности но не сама реальность. А это означает что у любой теории или модели есть границы применимости и погрешности, неизбежно с этим связанные. Так вот, мне не совсем ясно, для чего нам нужно ломать все "здание физики" только потому, что некоторые формулы можно уточнить? То есть, когда, скажем, в 40х годах придумали КЭД, это вовсе не отменило законов геометрической оптики, более того, масса чудесных формул продолжают использовать в оптике без каких либо изменений. Почему никому в голову не пришло рассчитывать, скажем, реальную линзу френеля при помощи КЭД? Это попросту невозможно. Такой вычислительной мощи не то чтобы нет, ее не будет никогда. Каждая модель годится для своей области применимости, и за этим границами ее использование бессмысленно. Формула колебаний струны, или уравнения Максвелла. вполне возможно могут быть уточнены членами следующего порядка малости. Однако возникает вопрос, а что нам это даст, кроме лишних вычислений? Для чего нужно считать обмены фотонами, электронами, и т.д. каждого атома тонны груза, который везет грузовки, если можно применить хорошо известные формулы механики? (причем даже не релятивистской). Однако, перехожу к вопросам

Вот Вы пытаетесь показать, что уравнение колебаний струны не вполне верно. Тогда объясните пожалуйста, смысл ваших слов, о "силе", с которой волна от источника действует на элемент среды. Что это за сила и откуда она берется. Раз уж мы собрались обсуждать ошибки в основах, давайте определимся с самым простым явлением. Что, каким образом и на что действует.
И второй вопрос. А почему,собственно, уравнение колебания струны должно отменить квантовую механику? Каким образом "ошибки" в понимании волновых процессов ставят под сомнение верность постулатов квантовой механики?

Цитата: TIR от 21.04.2011 18:43:25
Вопрос не нов.
Л. А. Молотков. О распространении упругих волн от неравномерно движущегося источника. МИАН СССР 1967 г.

Не понял, что Вы этим хотели сказать. Сформулируйте вопрос в явном виде.

Цитата: mozgi от 22.04.2011 08:31:21
Хочется задать два простых вопроса...
Но перед этим замечу вот что. Пытаюсь проникнуть мыслью внутрь тех противоречий, что тут описываются, и, по правде говоря, не очень удается. Вообще трудности для понимания вызывает вот какая вещь, если мы считаем, что математический аппарат, он же фундамент физики, в нашей дискуссии, неверен, то отчего же он позволяет предсказать результаты эксперимента с приемлемой точностью? Ведь критерием удовлетворительности любой теории является соответствие предсказываемых ею результатов с экспериментальными данными. Я позволю себе напомнить, что чаще всего в физике сначала появляется идея, а уж затем математический аппарат, ее описывающий. Здесь же, нам предлагается пойти обратным путем, сначала решить уравнения, а из них вывести теорию. Более того, физика - это всегда упрощение, а отнюдь не усложнение. Все физические теории, все до единой, являются некой абстракцией, моделью, грубо описывающей реальность. Все эти теории по определению есть приближение к реальности но не сама реальность. А это означает что у любой теории или модели есть границы применимости и погрешности, неизбежно с этим связанные. Так вот, мне не совсем ясно, для чего нам нужно ломать все "здание физики" только потому, что некоторые формулы можно уточнить? То есть, когда, скажем, в 40х годах придумали КЭД, это вовсе не отменило законов геометрической оптики, более того, масса чудесных формул продолжают использовать в оптике без каких либо изменений. Почему никому в голову не пришло рассчитывать, скажем, реальную линзу френеля при помощи КЭД? Это попросту невозможно. Такой вычислительной мощи не то чтобы нет, ее не будет никогда. Каждая модель годится для своей области применимости, и за этим границами ее использование бессмысленно. Формула колебаний струны, или уравнения Максвелла. вполне возможно могут быть уточнены членами следующего порядка малости. Однако возникает вопрос, а что нам это даст, кроме лишних вычислений? Для чего нужно считать обмены фотонами, электронами, и т.д. каждого атома тонны груза, который везет грузовки, если можно применить хорошо известные формулы механики? (причем даже не релятивистской). Однако, перехожу к вопросам

Вот Вы пытаетесь показать, что уравнение колебаний струны не вполне верно. Тогда объясните пожалуйста, смысл ваших слов, о "силе", с которой волна от источника действует на элемент среды. Что это за сила и откуда она берется. Раз уж мы собрались обсуждать ошибки в основах, давайте определимся с самым простым явлением. Что, каким образом и на что действует.
И второй вопрос. А почему,собственно, уравнение колебания струны должно отменить квантовую механику? Каким образом "ошибки" в понимании волновых процессов ставят под сомнение верность постулатов квантовой механики?

Ваши вопросы преждевременны. Скоро я начну говорить об ошибках, а пока что это введение. Просто у меня нет времени детально все написать - это требует большой концентрации, а на меня навалилось множество проблем.

Цитата: Yuri Rus от 22.04.2011 12:25:19
Не понял, что Вы этим хотели сказать. Сформулируйте вопрос в явном виде.

Это не вопрос, а констатация. Тема о продольных, поперчных и иных составляющих волн от движущегося источника в упругих средах не нова.
Если хотите именно вопрос, извольте - знакомы ли Вы с трудами исследователей этой тематики, и если да, то есть ли среди них Ваши единомышленники относительно необходимости разрушения фундамента Физики?
(Я поправил ссылку в моем предыдущем посте).

Цитата: TIR от 23.04.2011 00:04:43
Это не вопрос, а констатация. Тема о продольных, поперчных и иных составляющих волн от движущегося источника в упругих средах не нова.
Если хотите именно вопрос, извольте - знакомы ли Вы с трудами исследователей этой тематики, и если да, то есть ли среди них Ваши единомышленники относительно необходимости разрушения фундамента Физики?
(Я поправил ссылку в моем предыдущем посте).

Статей и книг об одновременном распространении продольных и поперечных волн множество. Те же волны на поверхности воды имеют и те, и другие компоненты (а вода это не упругая среда). С какими-то работами на эту тему я знаком, но, конечно, лишь с малой частью. Все, что я читал, разумеется, находится в рамках "официальной физики" и сомнению ее не подвергает. Очень сомневаюсь, что среди авторов таких работ есть хоть кто-нибудь, кто считает, что фундамент физики неверен и его требуется заменить. Впрочем, если бы кто-то так считал, его выгнали бы из профессии и ничего он не смог бы опубликовать (до появления интернета). Но открытие такого рода настолько значимо, что человек, совершивший его, рано или поздно рискнул бы это обнародовать, даже рискуя своей карьерой в физике. Психологически, первооткрывателю было бы невозможно всю жизнь молчать о таком открытии.

Я о таком не слыхал. Я очень внимательно изучал все статьи и книги, которые относятся к жанру "альтернативная физика", именно потому, что я пришел к выводу, что официальная физика неверна, а значит, только работы ее критиков имеют интерес. Но ни разу я не встретил ничего похожего на те ошибки физики и математики, которые обнаружил я.

Я в принципе закончил с введением и скоро буду писать о самих ошибках. Давайте дискутировать уже после этого.

И общее сообщение для всех, у кого могут возникнуть вопросы. Вопросам я, конечно, рад, потому что они показывают интерес к тому, что я пишу. Но на многие вопросы я не могу ответить сразу же, как только они были заданы. Не столько даже из-за отсутствия времени, сколько из-за того, что ответ будет очень длинным и я все равно собираюсь на эту тему говорить несколько позже, когда в своем изложении я дойду до этого момента. Поэтому часто я так и напишу - ответ будет позже, после того, как я сформулирую определенные вещи.

Например, на первой странице ветки Поверонов спросил меня, в чем подвох с формулой полного дифференциала, это ведь чистая математика. Я ответил: "Вот именно - "чистая математика". Об этом я и хочу говорить - как "чистая математика" приводит к совершенно неверным выводам. Мне для этого понадобится некоторое время, все написать."

Написал я об этом только через месяц. И текст был весьма длинным. Именно поэтому я не стал отвечать ему сразу - потому что я знал, что ответ должен быть очень длинным, а в тот момент он был еще не дописан.

Особенно я не хочу отвечать коротко на принципиально важные вопросы. Они заслуживают уважительного отношения к себе, детального объяснения. Потому писать я буду не торопясь, потихоньку, уделяя основное внимание последовательности и логике изложения, а не скакать с вопроса на вопрос. Вот после того, как основные положения моей теории будут сформулированы, можно и поскакать. Сейчас же до этого еще далеко - как я уже не раз писал, я могу уделять написанию лишь малую часть своего времени, а кроме того, я не умею писать быстро, переделываю важный текст много раз.

Цитата: problemsolver
<skip>
Вообще, моя теория мира гласит, что наше трехмерное пространство просто пересекает n-мерные волны, и все частицы, типа кварков, и все поля и взаимодействия - всего лишь следствие взаимодействия волн бОльших размерностей. И мы пока что можем только теоретически прикинуть, что происходит. До экспериментов по воздействию на эти многомерные волны еще далеко. Никому даже в голову такое не приходит )

Чем-то это напоминает теорию струн . Там размерность = 26. И вымучивают ее теоретики с 1970-х.
Правда с экспериментальным подтверждением у них обстоит также как и у Вас

Цитата: problemsolver
Ну блин же. А как еще я могу назвать теорию, которая собирается описать всё? Какая другая терминология есть?

В том-то и дело, что я НЕ претендую, что моя теория описывает "всё". Я это и подчеркнул в своем ответе. Я всего лишь хочу показать, что в фундаменте физики имеются ошибки, которые делают большинство ее построений неверными. Я выскажу свои мысли о том, КАК следует строить новую физику, положу несколько первых камешков в фундамент. И - всё. Я не построю новое здание всё целиком. Это сделают другие - если я смогу их убедить, что старое здание фальшиво.

Тот же Коперник: насколько я помню, он не построил математическую теорию, которая была способна предсказывать движения планет и т.д. с той же точностью, как теория Птолемея со всеми эпициклами. Для построения такой теории, понадобились усилия многих ученых и длительное время.

Цитата: problemsolver
Не кидайтесь на людей, которые не аплодируют вам, мне просто интересно.

Разве я кидался? Мне кажется, ответил вполне спокойно. Я даже на тех, кто мне будет хамить, кидаться не буду, просто не стану с ними разговаривать.

Цитата: problemsolver
Вообще, моя теория мира гласит, что наше трехмерное пространство просто пересекает n-мерные волны, и все частицы, типа кварков, и все поля и взаимодействия - всего лишь следствие взаимодействия волн бОльших размерностей. И мы пока что можем только теоретически прикинуть, что происходит. До экспериментов по воздействию на эти многомерные волны еще далеко. Никому даже в голову такое не приходит )

Это довольно далеко от моих представлений.

Ув. Юрий.
К сожалению в в Вашем сообщении изначально нет презентации, что конечно сохраняет интригу но не способствует привлечению интересующихся данной тематикой. Свежие идеи всегда интересны. Попробую сам догадаться и сформулировать тезисы:
1 некоторые математические модели в физике не правильные
2некоторое понимание некоторых  физических явлений неправильное
3существует некий математический аппарат в природе отличный от известного нам аппарата и у вас есть его базовый фундамент и вы нам предлагаете его понять и доработать
С вами полностью согласен скажу больше, придуманное недавно человечеством дифференциальное и интегральное исчисление (не знамши его египтянам это не помешало строить пирамиды), которым вы начали свое доказательство вводной лекцией природа тоже не пользует - существует другой механизм (не знамши его мы летаем в космос).
Если я вас правильно понял жду дальнейших ваших постов с горячим желанием познать мироздание....
П.С. а как должно выглядеть приобразование Фурье в новой математике у вас есть уже решение?  ::)

Цитата: Mikky Mouse от 25.04.2011 01:50:25
Ув. Юрий.
К сожалению в в Вашем сообщении изначально нет презентации, что конечно сохраняет интригу но не способствует привлечению интересующихся данной тематикой. Свежие идеи всегда интересны. Попробую сам догадаться и сформулировать тезисы:
1 некоторые математические модели в физике не правильные
2некоторое понимание некоторых  физических явлений неправильное
3существует некий математический аппарат в природе отличный от известного нам аппарата и у вас есть его базовый фундамент и вы нам предлагаете его понять и доработать

Ув. Mikky Mouse, я делаю значительно более сильные утверждения.

1. Большинство фундаментальных физических уравнений, моделей, математических понятий принципиально неверно. Например, неверны основные понятия векторного анализа - трехмерные (пространственные) градиент, ротор, дивергенция, способы интегрирования по объему, по поверхности, по кривой - имеют смысл только для статики, а для динамики, если объекты двигаются, они просто не имеют ни физического, ни математического смысла. Намек - эти понятия должны включать в себя не только пространственные переменные, но и обязательно временные. Причем для динамики, уравнения должны включать в себя намного больше пространственных и временных переменных, чем 3+1.

2. Физика как наука почти полностью неверна. Очень многие реально существующие явления физикой не замечаются, а те явления, которые физика считают существующими и которые и составляют главное содержание современной (и классической, в меньшей степени) физики, на самом деле, не существуют.

3. Я обнаружил эти фундаментальные ошибки физики, используя ее нынешний математический аппарат, в его рамках. Уже потом, размышляя о причинах, почему эти ошибки были столь долго не замечены, я постепенно пришел к выводу, что причина в математике, что нужен новый математический аппарат, и у меня появились некоторые соображения, в чем могут быть его отличия от существующего.

В следующих своих сообщениях, я как раз хочу показать некоторые важные ошибки физики, оставаясь в рамках "старой" физики, пользуясь старым мат. аппаратом. Вот тогда уже обсуждение будет иметь смысл. А сейчас, пока я этого еще не сделал, обсуждать, собственно, нечего. Да, я пишу очень медленно, но что поделать. Быстрее не получается.

Цитата: Mikky Mouse от 25.04.2011 01:50:25
С вами полностью согласен скажу больше, придуманное недавно человечеством дифференциальное и интегральное исчисление (не знамши его египтянам это не помешало строить пирамиды), которым вы начали свое доказательство вводной лекцией природа тоже не пользует - существует другой механизм (не знамши его мы летаем в космос).
Если я вас правильно понял жду дальнейших ваших постов с горячим желанием познать мироздание....
П.С. а как должно выглядеть приобразование Фурье в новой математике у вас есть уже решение?  ::)

Да в общем-то и птицы с насекомыми умеют летать, не зная аэродинамики и дифференциального/интегрального исчисления, и рыбы плавают. Можно и без науки жить, кто ж спорит.

До преобразования Фурье я пока не дошел. Заранее понятно, что для динамики оно будет выглядеть намного сложнее (многомернее), и потому не очевидно, что использование нового преобразования Фурье даст какие-то преимущества при решении численных задач.

Цитата: Yuri Rus
Надо же, какой нервный пациент. Я ему отвечаю, что отвечу позже, потому что сначала мне надо будет сформулировать ряд вещей, а до того - бессмысленно переливать из пустого в порожнее, а он сразу прыгает к глобальным выводам.

Будьте уж любезны, сдержите свое слово и здесь больше не показывайтесь. Срачем и флудом я заниматься не собираюсь.

Это замечательно, честное слово. Спасибо, я оценил Ваше умение манипулировать сознанием и приписывать оппонентам слова, которых они не говорили, с целью выключить их из дискуссии. Не стоит злоупотреблять такими приемами, лучше уж говорите то, что думаете, так честнее будет.
Мои нервы оставим в покое, равно как и мой статус пациента той или иной клиники, не будем спускаться до "срача и флуда" по Вашему же выражению.
Однако мне совершенно неясно Ваше упорное нежелание ответить на элементарный вопрос. Собственно отсутствие простого ответа на простой вопрос, по моему мнению и делает эту дискусиию далекой от физики. Если же я недостаточно ясно выразился в формулировке вопроса в прошлый раз, то вот он еще раз. Оставим пока в покое квантовую механику и причины, по которой она стала неверна. Простой вопрос что такое "сила", с которой волна действует на элемент среды? Не надо, пожалуйста ссылаться на то, что это - введение и вопросы на ответы будут даны позже. Вы пользуетесь неким определением явления вот и разъясните его тогда. Лично для меня, волна, особенно в случае колебаний струны, который Вы разбираете в своем "введении" является просто некой абстракцией облегчающей дальнейшие вычисления. Абстракция означает что волны как таковой нет, ее не существует, а вместо нее существует возмущение, распространяющееся в среде. И это возмущение имеет некоторую форму, которую можно описать. Однако сказать что "волна действует на элемент среды" примерно то же самое что сказать что форма действует с силой на материальное тело. Суть такого, с позволения сказать, явления для меня остается загадкой. Причем заметьте, не я а Вы вводите такое понятие в своем "введении". Так в чем же проблема объяснить это явление в двух словах? Или все-таки это не волна действует на элемент среды, а всего лишь соседний с ней элемент? Поясните свою мысль, уж будьте любезны.

А вот в следующем пассаже вы говорите следующее:

Цитата: Yuri Rus от 25.04.2011 05:33:37
Ув. Mikky Mouse, я делаю значительно более сильные утверждения.

1. Большинство фундаментальных физических уравнений, моделей, математических понятий принципиально неверно. Например, неверны основные понятия векторного анализа - трехмерные (пространственные) градиент, ротор, дивергенция, способы интегрирования по объему, по поверхности, по кривой - имеют смысл только для статики, а для динамики, если объекты двигаются, они просто не имеют ни физического, ни математического смысла. Намек - эти понятия должны включать в себя не только пространственные переменные, но и обязательно временные. Причем для динамики, уравнения должны включать в себя намного больше пространственных и временных переменных, чем 3+1.

Опять таки, вопрос о невхождении "временных переменных" пока оставим в покое и попробуем понять, что Вы имеете ввиду, когда говорите о неверности понятия градиента, к примеру? Сейчас даже не будем говорить о роторе и дивергенции. Градиент это математический оператор. Он не может быть верным или не верным, как операция сложения. Просто люди в свое время договорились, что такие-то действия над функцией мы назовем градиентом. Все. Это правда все, о том как применять данный оператор и какие выводы на результатах его применения мы будем строить - уже наше дело. И тут могут быть и ошибочные выводы и ошибки в рассчетах и т.д. Но как может быть неверен оператор? Уж будьте так добры, объясните. Я надеюсь, верность операций в арифметике мы не будем ставить под сомнение?

Да в общем-то и птицы с насекомыми умеют летать, не зная аэродинамики и дифференциального/интегрального исчисления, и рыбы плавают. Можно и без науки жить, кто ж спорит.

Не в этом спор.
Какраз создатель (природа) и знает и  умеет это создавать,а мы нет, исходя только из аэродинамики строим жалкое подобие мухи не умеющее и 1/10 ее возможностей (упрощенная модель) .
А вы говорите можно и без науки жить.
Ну а по поводу вашей книги. Можно написать, вопрос будет ли она востребована сейчас или как с Галилем через 200 лет.
Год назад скончался интересный ученный
Reference
25лет потративший на пробивание своих идей. 2 академических образования физика и биология самостоятельно изучил астрофизику и геохимию. 3 книги, уйма научных статей. Его  теории объясняют многие несостыковки математических расчетов с реальными природными явлениями. Итог : вывод академической науки - дилетант, лженаука. ...Когда они будут востребованы?...
вот его  глава о современной математике
 http://cognitology.n…atemat.htm
П.С.  ... да,  и пока наш Юрий дописывает очередную главу своего эссе предлагаю в перерыве и другим  неравнодушным ( душевным ) пациентам присоединиться к дискуссии.

Цитата: Mikky Mouse от 25.04.2011 23:40:05
<skip>
вот его  глава о современной математике
 http://cognitology.n…atemat.htm
П.С.  ... да,  и пока наш Юрий дописывает очередную главу своего эссе предлагаю в перерыве и другим  неравнодушным ( душевным ) пациентам присоединиться к дискуссии.

Упреки А.Н. БАРБАРАШ к математике не совсем по адресу. Математики развивают и исследуют именно внутренние закономерности своих моделей. А  "запредельным" их применением грешат уже сами прикладные науки, пытающиеся применять математический аппарат. И то, что очень часто они применяют его не по делу, за рамками применимости математических моделей, как справедливо отмечает А.Н. БАРБАРАШ, есть следствие недостаточной математической культуры самих прикладников. Известно, что математика - самый нелюбимый предмет среди студентов всех специальностей, кроме математических факультетов, разумеется. Как учат, так и применяют.
И я вполне допускаю, что утверждения Юрия о допущенных физиками математических ошибках могут оказаться справедливыми.
Сплошь и рядом физики грешат расширением результатов за пределы доказанной области применения. Например, известный закон сохранения энергии выведен в теоретической механике только для строго изолированных систем и в предположении однородности времени. А изолированные системы  на Земле еще надо поискать. Однородность времени в гравитационных полях поставлена под сомнение той же общей теорией относительности. Вместе с тем, не затрудняя себя доказательствами изолированности рассматриваемых систем, и не взирая на гравитацию, повсеместно закон сохранения энергии возводится физиками во всеобщий абсолют. В физике спокойно могут сосуществовать и ОТО, и закон сохранения энергии, несмотря на то, что математически одно отрицает другое. Просто делают вид, что там где сохраняется энергия нет гравитации, а там где есть гравитация не уместен закон сохранения энергии, и чувствует себя очень уверенно в этакой невесомости.

Цитата: Mikky Mouse от 25.04.2011 23:40:05
Да в общем-то и птицы с насекомыми умеют летать, не зная аэродинамики и дифференциального/интегрального исчисления, и рыбы плавают. Можно и без науки жить, кто ж спорит.

Не в этом спор.
Какраз создатель (природа) и знает и  умеет это создавать,а мы нет, исходя только из аэродинамики строим жалкое подобие мухи не умеющее и 1/10 ее возможностей (упрощенная модель) .
А вы говорите можно и без науки жить.

Жить без науки - можно. Как животные. Именно это я имел в виду.

Цитата: Mikky Mouse от 25.04.2011 23:40:05
Ну а по поводу вашей книги. Можно написать, вопрос будет ли она востребована сейчас или как с Галилем через 200 лет.

Вот в том-то и дело. Потому я и не торопился публиковать свои идеи, что не верю, что наука/ученые примут их сейчас, а не через десятилетия. Потому я и задумался о такой демонстрации справедливости моей теории, как искусственная гравитация. Теория сама по себе, сколь бы доказательной она ни была, не способна поколебать привычные воззрения.

Цитата: Mikky Mouse от 25.04.2011 23:40:05
Год назад скончался интересный ученный
http://freakopedia.ru/wiki/%D0%91%D0%B0%D1%80%D0%B1%D0%B0%D1%80%D0%B0%D1%88_%D0%90%D0%BD%D0%B0%D1%82%D0%BE%D0%BB%D0%B8%D0%B9_%D0%9D%D0%B8%D0%BA%D0%B8%D1%84%D0%BE%D1%80%D0%BE%D0%B2%D0%B8%D1%87
25лет потративший на пробивание своих идей. 2 академических образования физика и биология самостоятельно изучил астрофизику и геохимию. 3 книги, уйма научных статей. Его  теории объясняют многие несостыковки математических расчетов с реальными природными явлениями. Итог : вывод академической науки - дилетант, лженаука. ...Когда они будут востребованы?...
вот его  глава о современной математике
 http://cognitology.n…atemat.htm
П.С.  ... да,  и пока наш Юрий дописывает очередную главу своего эссе предлагаю в перерыве и другим  неравнодушным ( душевным ) пациентам присоединиться к дискуссии.

О Барбараше я даже не слышал, что как раз и показывает, насколько трудно пробить стену одиночке, ставящему под сомнение старые догмы. С большинством того, что он пишет в этой главе о математике, я согласен. Почитаю его работы, возможно, будут мне полезны. Спасибо.

Смена парадигмы никогда не приветствуется апологетами "нормальной науки" и, как известно, большинство из них так до конца своей жизни и не принимает новую парадигму. Смена парадигм происходит только со сменой поколений (Планк, если не ошибаюсь). Но, боюсь, не всегда - далеко не все более правильные новые парадигмы побеждают менее правильные старые, многие так и остаются почти никому не известными из-за сопротивления "нормальной науки". Во второй половине ХХ века, в связи с усилением административного контроля над наукой (я не имею в виду со стороны правительств, нет - со стороны самих же ученых, Peer Review), стало почти невозможным опубликовать новые, революционные работы, опровергающие признанные догмы науки. Только появление интернета нарушило эту монополию и сейчас все-таки есть шансы на дальнейшее развитие науки, потому что оно возможно только путем смены парадигм.