Жизнь, Разум, Человек, Религия и Наука
149,922
565
24 года
Карма: 0.00
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Цитата: Поверонов от 26.04.2011 02:33:46
Известно, что математика - самый нелюбимый предмет среди студентов всех специальностей, кроме математических факультетов, разумеется. Как учат, так и применяют.
И в этом самая большая проблема самой математике которая стремиться не дать инженерам свой аппарат применительно к их специальности а некий набор стандартных абстрактных математических решений на все случаи жизни.
В итоге лишь на старших курсах студент проскочивший боком ВМ начинает самостоятельно заново ее изучать применительно к своей специальности. Что касается студентов математических специальностей там еще хуже - подготовка снобов небожителей изучивших божественный язык неподвластный простым смертным....Так они его потом и преподают....
Теперь выскажу мысль по поводу востребованость знаний и теорий не воспринимаемых обществом.
К сожалению революционные теории способные резко поднять уровни знаний и технологий в обществе тормозятся по моему мнению из за нескольких причин и невсегда из-за косности академической науки:
1Новая теория не дает мгновенного прорыва в знаниях
2Старая теория экспериментально полностью не опровергается а несостыковки опускаются за рамки расчетов
3Новая лже теория состыковывает старую теорию с несостыковками выявленными экспериментально
4Религиозный аспект
пример - теория большого взрыва http://barbarashan.narod.ru/razgovor.htm
– Что такое электричество? – спросил однажды профессор студента.– Я знал, но забыл, – ответил студент. – Какая потеря для человечества! – воскликнул профессор. – Никто в мире не знает, что такое электричество. Один человек знал, и тот забыл! Когда вы вс

64 года
Карма: +394.08
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Давайте рассмотрим, как распространяются волны в рамках «нулевого приближения». «Нулевое приближение» означает, что последовательные волны от движущегося источника не взаимодействуют; каждая единичная волна, испущенная в точке (ξ, η, ζ) в момент времени ԏ, распространяется радиально с фазовой скоростью с в покоящейся среде (в первом приближении, среда уже не покоится, но об этом мы будем говорить позже).
Именно так, собственно, и рассматривает распространение волн «официальная физика». С ее точки зрения, если источник покоится, векторы фазовой скорости с и лучей r всех волн направлены радиально из точки, где находится источник. Если источник движется, векторы с и r каждой излучаемой им единичной волны направлены по-прежнему радиально, но теперь не из точки, где находится источник в данный момент, а из точки, где был источник в момент излучения этой волны. Траектории, образуемые векторами с и r для каждой волны – прямые линии как для покоящегося, так и для движущегося источника.
Чтобы проиллюстрировать это, еще раз посмотрим на апплет для эффекта Доплера:
http://www.astro.ubc…ppler.html
Этот апплет показывает распространение фронтов волн от движущегося источника в системе отсчета, где среда покоится. Я сам не могу сделать апплет (я не программист), где распространение волн показано для системы отсчета, связанной с источником. Но это, наверно, и не требуется – достаточно слегка поворачивать голову по мере движения источника и представить себе, что источник покоится, а среда движется (встречный ветер со скоростью –Vи). Можно сказать, что тем самым вы мысленно проделаете преобразования Галилея.
Авторы апплета, я уверен, использовали алгебраическое волновое уравнение типа
(x – Vиt)² + y² + z² = c²(t – ԏ)² или r – rи = c(t – ԏ),
а не искали решение неоднородного дифференциального уравнения. Это было бы в тысячи раз сложнее, а результат, казалось бы, будет одинаков – зачем же мучиться?
Мгновенный снимок волн от движущегося источника, который я уже приводил, выглядит так:
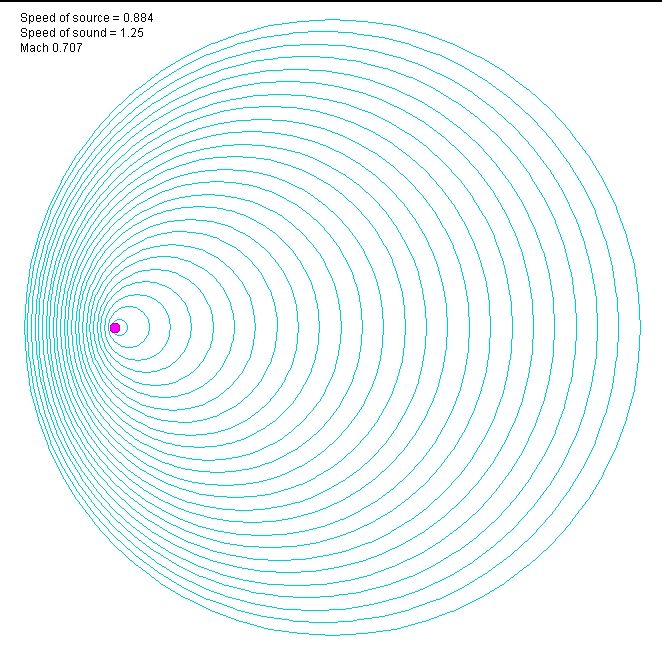
Запомним эту картинку, она нам еще не раз пригодится. Картинка эта, безусловно, имеет физический смысл (если кто-то не согласен, объясните, почему). Это я и имел в виду, когда ранее писал, что это простенькое алгебраическое волновое уравнение полезно использовать как «контроль на физический смысл», для качественной оценки волновых процессов.
Обратите внимание, еще раз – все волны сферические. Не сплюснутые в γ раз. В системе отсчета движущегося относительно среды источника, волны не выглядят так, как будто источник находится в покоящейся среде (где волны радиально распространяются из одного центра с одной и той же скоростью во всех направлениях). Эти сферические волны сдувает встречный ветер, поэтому спереди и сзади от источника волны выглядят отнюдь не симметрично.
Заметьте также, что если мы сделаем мгновенный снимок всех волн в какой-то момент времени, то этот снимок (форма каждой единичной волны и их расположение друг относительно друга) будет выглядеть абсолютно одинаково в обеих системах отсчета, покоящейся и движущейся. Это очень важно. Можно даже сформулировать это правило в виде закона:
Волновое уравнение инвариантно относительно преобразований Галилея. Все члены волнового уравнения должны выглядеть одинаково во всех инерциальных системах отсчета.
Откуда это следует? Ранее я писал, что волновое уравнение выводится из Второго Закона Ньютона и по сути является другой формой записи Второго Закона, эквивалентно ему. Каждый член волнового уравнения представляет собой ту или иную силу. А сила инвариантна относительно преобразований Галилея – вектор силы одинаков в любой инерциальной системе отсчета.
Приведу цитату из книги Гальцов Д.В., Грац Ю.В., Жуковский В.Ч. «Классические Поля», 1991, стр. 6-7:


Авторы этой книги, разумеется, ничего не пишут (и не подозревают, скорее всего) об инвариантности волнового уравнения относительно преобразований Галилея. Я привел эту цитату только для демонстрации самих преобразований Галилея, чтобы у читателя не было подозрений, что я что-то исказил. Инвариантность волнового уравнения – это мое утверждение. В учебниках физики я его не встречал.
Оно отнюдь не тривиально, потому что физика полна волновых уравнений в частных производных, которые выглядят совершенно иначе в разных системах отсчета. В частности, они описывают сжатие волн в γ раз, причем даже в нерелятивистском случае. Не будем пока трогать теорию относительности, ее постулаты и доказательства. Но к звуковым-то волнам преобразования Лоренца, сжатие в γ раз, казалось бы, не могут применяться? Это же – противоречит здравому смыслу?
Здравому смыслу, здравому смыслу. Тоже мне – аргумент. Когда это было препятствием для «настоящей физики» (помните выражение Нильса Бора о теории, достаточно сумасшедшей, чтобы быть правильной)? Физика, как известно, гордится тем, что теория относительности и квантовая механика противоречат здравому смыслу. Противоречие здравому смыслу буквально считается важнейшим достижением современной физики, доказательством высоты человеческого гения – ну как же, необузданный полет воображения привел к таким математическим формулам, физического смысла которых ни один человек не может себе представить. Можно только жонглировать математическими манипуляциями, а пытаться поставить им в соответствие какой-то мысленный образ, какие-то материальные (в смысле классической физики) объекты и процессы – признак глупости и непонимания физики. Есть только мат (math) – за него и держись.
Так вот, если последовательно, по-честному применять математические методы физики к переходу из одной инерциальной системы в другую, то никуда от гаммы и от сжатия звуковых волн вы не денетесь. Потому что они заложены в математическом фундаменте физики, а не в постулатах теории относительности или уравнениях Максвелла.
Продемонстрирую это на примере очень полезной для наших целей книги Блохинцева Д.И. «Акустика неоднородной движущейся среды» (1981), стр. 84-86:



Посмотрите на уравнения (3.12), (3.13) и (3.13'). Для источника, движущегося с дозвуковой скоростью v, автор получил сжатие звуковых волн в γ раз, где
γ = 1/(1 – (v/c) ²)½ , c – скорость звука, а не света.
Эти сжатые волны выглядят как центрально-симметричные эллипсоиды:
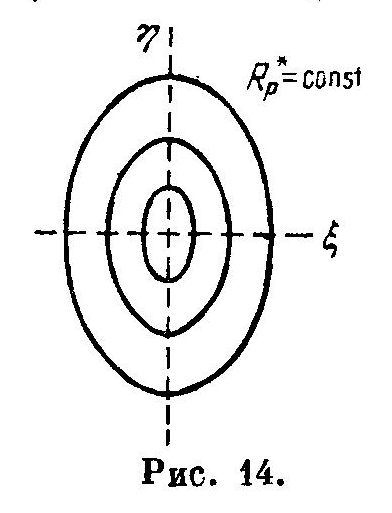

Это, опять же, полностью аналогично теории относительности.
Проверим уравнения Блохинцева на физический смысл. Посмотрим еще раз на апплет для эффекта Доплера, на мгновенный снимок всех волн от движущегося источника, на наш «контроль на физический смысл» r – rи = c(t – ԏ), и сравним с уравнениями Блохинцева. Имеет сжатие звуковых волн в γ раз какой-то физический смысл?
Категорически – нет, нет, нет! Ни в каком случае и никогда! Звуковые волны не бываютзеленого цвета эллиптическими, это вас кто-то обманул. Им полагается быть сферическими. В системе отсчета движущегося источника, их сдувает встречный ветер, из-за чего волновая картина (совокупность последовательных волн) не может быть центрально-симметричной. Даже если математика второй свежести утверждает обратное.
Сейчас физика – это не более чем раздел математики, играет подчиненную роль. А должно быть наоборот. Не может математика считаться истинной, если онатухлая явным образом противоречит реальному миру. Да, математик, основанных на разных аксиомах, может быть много. Но реальный мир, в котором мы живем, - только один. И потому истинной является только та математика, которая действительно соответствует этому реальному миру.
Поскольку, я предполагаю, читать меня будут не только физики, хочу сказать пару слов об авторе. Вот немного о Д.И. Блохинцеве (1908-1979) из Википедии:
«Окончил физический факультет Московского государственного университета (1930). Преподавал там же (с 1936 — профессор, затем заведующий кафедрой теоретической ядерной физики). Был создателем Отделения ядерной физики на физическом факультете МГУ. В 1935—1947 годах работал также в Физическом институте АН СССР (ФИАН). С 1947 года — директор научно-исследовательской лаборатории в Обнинске, на базе которой под его руководством создан Физико-энергетический институт. Руководитель Лаборатории «В» Министерства внутренних дел СССР (выполнение постановления «О проектировании и строительстве объекта 627»), позже на её базе создан ИЯИ РАН.
Был инициатором создания Объединённого института ядерных исследований (ОИЯИ) в Дубне. В 1956 году Комитет Полномочных Представителей одиннадцати стран единогласно избрал его первым директором этого института. В 1956—1965 годах — директор ОИЯИ, с 1965 года — директор Лаборатории теоретической физики ОИЯИ.
Научная деятельность
Работы посвящены теории твердого тела, физике полупроводников, оптике, акустике, квантовой механике и квантовой электронике, ядерной физике, теории ядерных реакторов, квантовой теории поля, физике элементарных частиц, философским и методологическим вопросам физики.
…
В 1944 году построил, исходя из уравнений газогидродинамики, теорию звуковых явлений в движущихся и неоднородных средах, получив уравнения акустики самого общего вида (уравнения Блохинцева), на основе которых вывел ряд акустических законов, объяснил и рассчитал разнообразные акустические явления в движущихся и неоднородных средах (в том числе турбулентных), касающихся, с одной стороны, механизма генерирования шума, а с другой — методов и средств его приема. Сформулировал уравнения геометрической акустики.
И многое другое.»
Так что не думайте, что я где-то раскопал побитую молью книжонку никому не известного автора и радостно хихикаю, что обнаружил там махонькую ошибочку. Это – фундамент данного раздела физики.
Именно так, собственно, и рассматривает распространение волн «официальная физика». С ее точки зрения, если источник покоится, векторы фазовой скорости с и лучей r всех волн направлены радиально из точки, где находится источник. Если источник движется, векторы с и r каждой излучаемой им единичной волны направлены по-прежнему радиально, но теперь не из точки, где находится источник в данный момент, а из точки, где был источник в момент излучения этой волны. Траектории, образуемые векторами с и r для каждой волны – прямые линии как для покоящегося, так и для движущегося источника.
Чтобы проиллюстрировать это, еще раз посмотрим на апплет для эффекта Доплера:
http://www.astro.ubc…ppler.html
Этот апплет показывает распространение фронтов волн от движущегося источника в системе отсчета, где среда покоится. Я сам не могу сделать апплет (я не программист), где распространение волн показано для системы отсчета, связанной с источником. Но это, наверно, и не требуется – достаточно слегка поворачивать голову по мере движения источника и представить себе, что источник покоится, а среда движется (встречный ветер со скоростью –Vи). Можно сказать, что тем самым вы мысленно проделаете преобразования Галилея.
Авторы апплета, я уверен, использовали алгебраическое волновое уравнение типа
(x – Vиt)² + y² + z² = c²(t – ԏ)² или r – rи = c(t – ԏ),
а не искали решение неоднородного дифференциального уравнения. Это было бы в тысячи раз сложнее, а результат, казалось бы, будет одинаков – зачем же мучиться?
Мгновенный снимок волн от движущегося источника, который я уже приводил, выглядит так:

Запомним эту картинку, она нам еще не раз пригодится. Картинка эта, безусловно, имеет физический смысл (если кто-то не согласен, объясните, почему). Это я и имел в виду, когда ранее писал, что это простенькое алгебраическое волновое уравнение полезно использовать как «контроль на физический смысл», для качественной оценки волновых процессов.
Обратите внимание, еще раз – все волны сферические. Не сплюснутые в γ раз. В системе отсчета движущегося относительно среды источника, волны не выглядят так, как будто источник находится в покоящейся среде (где волны радиально распространяются из одного центра с одной и той же скоростью во всех направлениях). Эти сферические волны сдувает встречный ветер, поэтому спереди и сзади от источника волны выглядят отнюдь не симметрично.
Заметьте также, что если мы сделаем мгновенный снимок всех волн в какой-то момент времени, то этот снимок (форма каждой единичной волны и их расположение друг относительно друга) будет выглядеть абсолютно одинаково в обеих системах отсчета, покоящейся и движущейся. Это очень важно. Можно даже сформулировать это правило в виде закона:
Волновое уравнение инвариантно относительно преобразований Галилея. Все члены волнового уравнения должны выглядеть одинаково во всех инерциальных системах отсчета.
Откуда это следует? Ранее я писал, что волновое уравнение выводится из Второго Закона Ньютона и по сути является другой формой записи Второго Закона, эквивалентно ему. Каждый член волнового уравнения представляет собой ту или иную силу. А сила инвариантна относительно преобразований Галилея – вектор силы одинаков в любой инерциальной системе отсчета.
Приведу цитату из книги Гальцов Д.В., Грац Ю.В., Жуковский В.Ч. «Классические Поля», 1991, стр. 6-7:


Авторы этой книги, разумеется, ничего не пишут (и не подозревают, скорее всего) об инвариантности волнового уравнения относительно преобразований Галилея. Я привел эту цитату только для демонстрации самих преобразований Галилея, чтобы у читателя не было подозрений, что я что-то исказил. Инвариантность волнового уравнения – это мое утверждение. В учебниках физики я его не встречал.
Оно отнюдь не тривиально, потому что физика полна волновых уравнений в частных производных, которые выглядят совершенно иначе в разных системах отсчета. В частности, они описывают сжатие волн в γ раз, причем даже в нерелятивистском случае. Не будем пока трогать теорию относительности, ее постулаты и доказательства. Но к звуковым-то волнам преобразования Лоренца, сжатие в γ раз, казалось бы, не могут применяться? Это же – противоречит здравому смыслу?
Здравому смыслу, здравому смыслу. Тоже мне – аргумент. Когда это было препятствием для «настоящей физики» (помните выражение Нильса Бора о теории, достаточно сумасшедшей, чтобы быть правильной)? Физика, как известно, гордится тем, что теория относительности и квантовая механика противоречат здравому смыслу. Противоречие здравому смыслу буквально считается важнейшим достижением современной физики, доказательством высоты человеческого гения – ну как же, необузданный полет воображения привел к таким математическим формулам, физического смысла которых ни один человек не может себе представить. Можно только жонглировать математическими манипуляциями, а пытаться поставить им в соответствие какой-то мысленный образ, какие-то материальные (в смысле классической физики) объекты и процессы – признак глупости и непонимания физики. Есть только мат (math) – за него и держись.
Так вот, если последовательно, по-честному применять математические методы физики к переходу из одной инерциальной системы в другую, то никуда от гаммы и от сжатия звуковых волн вы не денетесь. Потому что они заложены в математическом фундаменте физики, а не в постулатах теории относительности или уравнениях Максвелла.
Продемонстрирую это на примере очень полезной для наших целей книги Блохинцева Д.И. «Акустика неоднородной движущейся среды» (1981), стр. 84-86:



Посмотрите на уравнения (3.12), (3.13) и (3.13'). Для источника, движущегося с дозвуковой скоростью v, автор получил сжатие звуковых волн в γ раз, где
γ = 1/(1 – (v/c) ²)½ , c – скорость звука, а не света.
Эти сжатые волны выглядят как центрально-симметричные эллипсоиды:


Это, опять же, полностью аналогично теории относительности.
Проверим уравнения Блохинцева на физический смысл. Посмотрим еще раз на апплет для эффекта Доплера, на мгновенный снимок всех волн от движущегося источника, на наш «контроль на физический смысл» r – rи = c(t – ԏ), и сравним с уравнениями Блохинцева. Имеет сжатие звуковых волн в γ раз какой-то физический смысл?
Категорически – нет, нет, нет! Ни в каком случае и никогда! Звуковые волны не бывают
Сейчас физика – это не более чем раздел математики, играет подчиненную роль. А должно быть наоборот. Не может математика считаться истинной, если она
Поскольку, я предполагаю, читать меня будут не только физики, хочу сказать пару слов об авторе. Вот немного о Д.И. Блохинцеве (1908-1979) из Википедии:
«Окончил физический факультет Московского государственного университета (1930). Преподавал там же (с 1936 — профессор, затем заведующий кафедрой теоретической ядерной физики). Был создателем Отделения ядерной физики на физическом факультете МГУ. В 1935—1947 годах работал также в Физическом институте АН СССР (ФИАН). С 1947 года — директор научно-исследовательской лаборатории в Обнинске, на базе которой под его руководством создан Физико-энергетический институт. Руководитель Лаборатории «В» Министерства внутренних дел СССР (выполнение постановления «О проектировании и строительстве объекта 627»), позже на её базе создан ИЯИ РАН.
Был инициатором создания Объединённого института ядерных исследований (ОИЯИ) в Дубне. В 1956 году Комитет Полномочных Представителей одиннадцати стран единогласно избрал его первым директором этого института. В 1956—1965 годах — директор ОИЯИ, с 1965 года — директор Лаборатории теоретической физики ОИЯИ.
Научная деятельность
Работы посвящены теории твердого тела, физике полупроводников, оптике, акустике, квантовой механике и квантовой электронике, ядерной физике, теории ядерных реакторов, квантовой теории поля, физике элементарных частиц, философским и методологическим вопросам физики.
…
В 1944 году построил, исходя из уравнений газогидродинамики, теорию звуковых явлений в движущихся и неоднородных средах, получив уравнения акустики самого общего вида (уравнения Блохинцева), на основе которых вывел ряд акустических законов, объяснил и рассчитал разнообразные акустические явления в движущихся и неоднородных средах (в том числе турбулентных), касающихся, с одной стороны, механизма генерирования шума, а с другой — методов и средств его приема. Сформулировал уравнения геометрической акустики.
И многое другое.»
Так что не думайте, что я где-то раскопал побитую молью книжонку никому не известного автора и радостно хихикаю, что обнаружил там махонькую ошибочку. Это – фундамент данного раздела физики.
Отредактировано: Yuri Rus - 21 ноя 2019 03:20:33

64 года
Карма: +394.08
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Итак, если уравнения Блохинцева неверны, где же в них ошибка? Вот здесь:
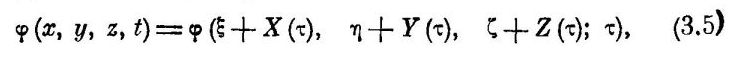

Переход от одной инерциальной системы отсчета к другой осуществлен неверно (это не ошибка Блохинцева, это фундаментальная ошибка всей физики). Дело в том, что функция φ должна зависеть не только от переменных (x, y, z, t), но и от координат источника (ξ, η, ζ, ԏ):
φ = φ(x, y, z, t, ξ, η, ζ, ԏ).
Это неважно, что переменные (ξ, η, ζ, ԏ) можно выразить через (x, y, z, t):
ξ = X(t) по оси х
η = Y(t) по оси у
ζ = Z(t) по оси z
ԏ = t
Как я объяснял на первой странице ветки:
Если источник движется по прямой линии, то оси координат можно выбрать так, чтобы движение происходило только по оси x, а η и ζ в любой момент времени были равны нулю. Тогда их можно исключить из рассмотрения и остаются только x, y, z, ξ, t, ԏ. Если, далее, источник движется с постоянной скоростью v₀, мы можем выразить ξ через ԏ: ξ = v₀ԏ. Это, однако, не позволит нам избавиться и от ξ тоже, поскольку ξ остается переменной. Избавиться можно только от тех переменных, которые в любой момент времени равны нулю или константе. Таким образом, минимальное количество пространственных координат для описания источника, движущегося по прямой линии, должно быть 4, а временных координат – 2.
Сейчас я хочу обратить ваше внимание на то, что здесь дело не в том, что можно выбрать оси координат так, чтобы избавиться от каких-то пространственных координат. Дело в том, что все эти 6 пространственных координат (x, y, z, ξ, η, ζ) принадлежат одной и той же системе отсчета. Остановитесь и подумайте над этой фразой. Это то, чего не понимает физика – ни классическая, ни релятивистская. Более того –теория относительности родилась на свет, в сущности, именно из-за этой ошибки (не только – есть и другие ошибки, но эта одна из важнейших).
Давайте разберемся, как же следует правильно переходить из одной инерциальной системы отсчета в другую (не связанную с источником). Обозначим пространственные координаты системы отсчета, где среда покоится, как (x₀, y₀, z₀, ξ₀, η₀, ζ₀), а некой движущейся системы отсчета – как (x₁, y₁, z₁, ξ₁, η₁, ζ₁). Для простоты, выберем оси (x₁, y₁, z₁, ξ₁, η₁, ζ₁) параллельными осям (x₀, y₀, z₀, ξ₀, η₀, ζ₀). Пусть вторая СО движется относительно покоящейся СО со скоростью v₁ с компонентами (v₁₁, v₁₂, v₁₃) по осям (x₀, y₀, z₀). Временные координаты t и ԏ одинаковы для обеих систем отсчета (то есть мы не вводим отдельно t₀, ԏ₀ и t₁, ԏ₁).
Переход из одной системы отсчета в другую осуществляется следующим образом:
x₁ = x₀ – v₁₁ԏ + C₁
y₁ = y₀ – v₁₂ԏ + C₂
z₁ = z₀ – v₁₃ԏ + C₃
ξ₁ = ξ₀ – v₁₁ԏ + C₄
η₁ = η₀ – v₁₂ԏ + C₅
ζ₁ = ζ₀ – v₁₃ԏ + C₆
где C₁, C₂, C₃, C₄, C₅, C₆ – некие константы. Чтобы они не мешались, примем их все равными нулю. Это не принципиально, а загромождать уравнения не стоит.
Тогда обратный переход:
x₀ = x₁ + v₁₁ԏ
y₀ = y₁ + v₁₂ԏ
z₀ = z₁ + v₁₃ԏ
ξ₀ = ξ₁ + v₁₁ԏ
η₀ = η₁ + v₁₂ԏ
ζ₀ = ζ₁ + v₁₃ԏ
Вместо
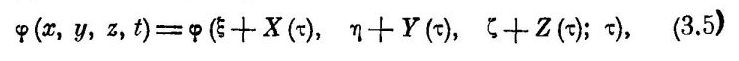
будет
φ(x₀, y₀, z₀, ξ₀, η₀, ζ₀, t, ԏ) = φ(x₁ + v₁₁ԏ, y₁ + v₁₂ԏ, z₁ + v₁₃ԏ, ξ₁ + v₁₁ԏ, η₁ + v₁₂ԏ, ζ₁ + v₁₃ԏ, t, ԏ)
Повторяя манипуляции Блохинцева, получим:
∂φ/∂x₀ = ∂φ/∂x₁ ∂φ/∂y₀ = ∂φ/∂y₁ ∂φ/∂z₀ = ∂φ/∂z₁
∂φ/∂ξ₀ = ∂φ/∂ξ₁ ∂φ/∂η₀ = ∂φ/∂η₁ ∂φ/∂ζ₀ = ∂φ/∂ζ₁
И то же самое для вторых производных:
∂²φ/∂x₀² = ∂²φ/∂x₁² ∂²φ/∂y₀² = ∂²φ/∂y₁² ∂²φ/∂z₀² = ∂²φ/∂z₁²
∂²φ/∂ξ₀² = ∂²φ/∂ξ₁² ∂²φ/∂η₀² = ∂²φ/∂η₁² ∂²φ/∂ζ₀² = ∂²φ/∂ζ₁²
С частной производной по времени несколько сложнее:
∂φ/∂t = ∂φ/∂ԏ - v₁₁(∂φ/∂x₁) - v₁₂(∂φ/∂y₁) - v₁₃(∂φ/∂z₁) - v₁₁(∂φ/∂ξ₁) - v₁₂(∂φ/∂η₁) - v₁₃(∂φ/∂ζ₁)
Я ранее уже писал, что поскольку x и ξ, y и η, z и ζ, t и ԏ всегда встречаются парами:
f = f(x - ξ, y - η, z - ζ, t - ԏ),
то нетрудно убедиться, что
Df = (∂f/∂x)(dx – dξ) + (∂f/∂y)(dy – dη) + (∂f/∂z)(dz – dζ) + (∂f/∂t)(dt – dԏ)
Хотя это очень просто, на всякий случай, я объясню, почему это так.
Допустим, у нас есть функция f от двух переменных p и s, причем в уравнении фигурирует именно их разность: f = f(p – s). Например, f = (p – s)³, или f = ln²(p – s), или f = sin²(p – s), и т.д.
Введем замену переменных: q = p – s. А теперь заметим, что частные производные ∂f/∂p и ∂f/∂s можно выразить через производную df/dq следующим образом:
∂f/∂p = (df/dq) (∂/∂p) (p – s) = df/dq
∂f/∂s = (df/dq) (∂/∂s) (p – s) = – df/dq
Что означает, в то же время, что
∂f/∂p = – ∂f/∂s
Итак, если мы запишем уравнение
∂φ/∂t = ∂φ/∂ԏ - v₁₁(∂φ/∂x₁) - v₁₂(∂φ/∂y₁) - v₁₃(∂φ/∂z₁) - v₁₁(∂φ/∂ξ₁) - v₁₂(∂φ/∂η₁) - v₁₃(∂φ/∂ζ₁)
как
∂φ/∂t = ∂φ/∂ԏ - v₁₁(∂φ/∂x₁ + ∂φ/∂ξ₁) - v₁₂(∂φ/∂y₁ + ∂φ/∂η₁) - v₁₃(∂φ/∂z₁ + ∂φ/∂ζ₁)
и произведем замены
∂φ/∂x₁ = – ∂φ/∂ξ₁
∂φ/∂y₁ = – ∂φ/∂η₁
∂φ/∂z₁ = – ∂φ/∂ζ₁
то это уравнение сокращается до
∂φ/∂t = ∂φ/∂ԏ
Далее, аналогично, легко получить
∂²φ/∂t² = ∂²φ/∂ԏ²
Что, собственно, и следовало ожидать, поскольку волновое уравнение, как и Второй Закон Ньютона, должно быть инвариантно относительно преобразований Галилея.
Здесь есть один нюанс. То, что сказано выше, относится к любой инерциальной системе отсчета – кроме системы отсчета движущегося источника. Потому что координаты (ξ₁, η₁, ζ₁) в этой системе отсчета равны нулю. Источник находится в начале координат и он, по определению, неподвижен. Это, в принципе, понятно и без всяких преобразований, но можно написать и их (в обозначениях Блохинцева):
ξ₀ = X(t)
η₀ = Y(t)
ζ₀ = Z(t)
x₁ = x₀ – X(t)
y₁ = y₀ – Y(t)
z₁ = z₀ – Z(t)
ξ₁ = ξ₀ – X(t) = 0
η₁ = η₀ – Y(t) = 0
ζ₁ = ζ₀ – Z(t) = 0
Как же так? В всех остальных системах отсчета, мы имели 6 пространственных координат, а в системе отсчета источника – только 3? Куда же делись эти пространственные координаты?Эй, источник, координаты лишние есть? А если найду? Ты с какой системы отсчета?
Главное различие между СО покоящейся среды и СО движущегося источника заключается в том, что в СО источника есть встречный ветер со скоростью –v₁ и с компонентами (–v₁₁, –v₁₂, –v₁₃), который сносит все волны. В двух словах, именно в этом ветре и «спрятались» наши исчезнувшие координаты (ξ₁, η₁, ζ₁). Число переменных остается тем же. Подробно разбирать этот вопрос я сейчас не хочу. Сначала нам надо будет получить «правильное» волновое уравнение (точнее, то, что я считаю правильным). Но до этого нам надо будет проделать еще длинный путь.
Можно, конечно, заметить, что в любой другой движущейся СО ветер тоже есть, но есть и координаты (ξ₁, η₁, ζ₁). Но это-то как раз не проблема. Это аналогично тому, что, в зависимости от выбора направлений осей координат, вы можете описать прямую линию в одномерном пространстве, двухмерном или трехмерном. «Лишние» переменные возникают всегда, если направления осей и т.п. выбраны не самым оптимальным образом.
Подведем некоторый итог. Я постарался показать, что сжатие в γ раз возникает из-за того, что, во-первых, вместо полной функции φ(x, y, z, ξ, η, ζ, t, ԏ) используется единичная функция φ(x, y, z, t). Во-вторых, переход из одной инерциальной системы отсчета в другую осуществляется неправильно: должен быть переход от координат (x₀, y₀, z₀, ξ₀, η₀, ζ₀) к (x₁, y₁, z₁, ξ₁, η₁, ζ₁), а не от (x, y, z) к (ξ, η, ζ).
Это не ошибки только Блохинцева – это заложено в фундаменте физики, «спрятано» в ее математическом аппарате. Точно те же ошибки привели в свое время к выводу преобразований Лоренца, которые, напомню, были получены в рамках классической физики, без всяких постулатов о постоянстве скорости света во всех инерциальных системах отсчета и прочих философских интерпретаций полученных формул.
Мы получили очень важный результат: мы увидели, что преобразования Лоренца не вытекают из постулата об ограничении скорости движения материальных тел скоростью света, не вытекают они даже и из уравнений Максвелла. Потому что совершенно аналогичные уравнения были получены Блохинцевым для звуковых волн, которые никак не связаны с электромагнетизмом, а их скорость в миллион раз меньше скорости света. Преобразования Лоренца и Блохинцева вытекают из одного источника – из самых основ математики физики.
Блохинцев, вероятно, честно проделал те же самые математические манипуляции, к которым он привык в электродинамике, теории относительности, квантовой механике, – и получил тот же самый результат. Он, впрочем, остановился в полушаге от замедления времени у движущегося источника, но да ладно, простим ему это. Nobody’s perfect.
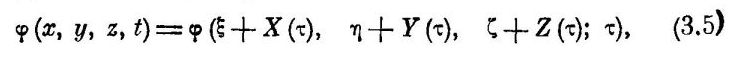

Переход от одной инерциальной системы отсчета к другой осуществлен неверно (это не ошибка Блохинцева, это фундаментальная ошибка всей физики). Дело в том, что функция φ должна зависеть не только от переменных (x, y, z, t), но и от координат источника (ξ, η, ζ, ԏ):
φ = φ(x, y, z, t, ξ, η, ζ, ԏ).
Это неважно, что переменные (ξ, η, ζ, ԏ) можно выразить через (x, y, z, t):
ξ = X(t) по оси х
η = Y(t) по оси у
ζ = Z(t) по оси z
ԏ = t
Как я объяснял на первой странице ветки:
Если источник движется по прямой линии, то оси координат можно выбрать так, чтобы движение происходило только по оси x, а η и ζ в любой момент времени были равны нулю. Тогда их можно исключить из рассмотрения и остаются только x, y, z, ξ, t, ԏ. Если, далее, источник движется с постоянной скоростью v₀, мы можем выразить ξ через ԏ: ξ = v₀ԏ. Это, однако, не позволит нам избавиться и от ξ тоже, поскольку ξ остается переменной. Избавиться можно только от тех переменных, которые в любой момент времени равны нулю или константе. Таким образом, минимальное количество пространственных координат для описания источника, движущегося по прямой линии, должно быть 4, а временных координат – 2.
Сейчас я хочу обратить ваше внимание на то, что здесь дело не в том, что можно выбрать оси координат так, чтобы избавиться от каких-то пространственных координат. Дело в том, что все эти 6 пространственных координат (x, y, z, ξ, η, ζ) принадлежат одной и той же системе отсчета. Остановитесь и подумайте над этой фразой. Это то, чего не понимает физика – ни классическая, ни релятивистская. Более того –теория относительности родилась на свет, в сущности, именно из-за этой ошибки (не только – есть и другие ошибки, но эта одна из важнейших).
Давайте разберемся, как же следует правильно переходить из одной инерциальной системы отсчета в другую (не связанную с источником). Обозначим пространственные координаты системы отсчета, где среда покоится, как (x₀, y₀, z₀, ξ₀, η₀, ζ₀), а некой движущейся системы отсчета – как (x₁, y₁, z₁, ξ₁, η₁, ζ₁). Для простоты, выберем оси (x₁, y₁, z₁, ξ₁, η₁, ζ₁) параллельными осям (x₀, y₀, z₀, ξ₀, η₀, ζ₀). Пусть вторая СО движется относительно покоящейся СО со скоростью v₁ с компонентами (v₁₁, v₁₂, v₁₃) по осям (x₀, y₀, z₀). Временные координаты t и ԏ одинаковы для обеих систем отсчета (то есть мы не вводим отдельно t₀, ԏ₀ и t₁, ԏ₁).
Переход из одной системы отсчета в другую осуществляется следующим образом:
x₁ = x₀ – v₁₁ԏ + C₁
y₁ = y₀ – v₁₂ԏ + C₂
z₁ = z₀ – v₁₃ԏ + C₃
ξ₁ = ξ₀ – v₁₁ԏ + C₄
η₁ = η₀ – v₁₂ԏ + C₅
ζ₁ = ζ₀ – v₁₃ԏ + C₆
где C₁, C₂, C₃, C₄, C₅, C₆ – некие константы. Чтобы они не мешались, примем их все равными нулю. Это не принципиально, а загромождать уравнения не стоит.
Тогда обратный переход:
x₀ = x₁ + v₁₁ԏ
y₀ = y₁ + v₁₂ԏ
z₀ = z₁ + v₁₃ԏ
ξ₀ = ξ₁ + v₁₁ԏ
η₀ = η₁ + v₁₂ԏ
ζ₀ = ζ₁ + v₁₃ԏ
Вместо
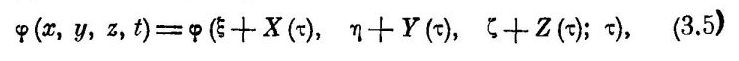
будет
φ(x₀, y₀, z₀, ξ₀, η₀, ζ₀, t, ԏ) = φ(x₁ + v₁₁ԏ, y₁ + v₁₂ԏ, z₁ + v₁₃ԏ, ξ₁ + v₁₁ԏ, η₁ + v₁₂ԏ, ζ₁ + v₁₃ԏ, t, ԏ)
Повторяя манипуляции Блохинцева, получим:
∂φ/∂x₀ = ∂φ/∂x₁ ∂φ/∂y₀ = ∂φ/∂y₁ ∂φ/∂z₀ = ∂φ/∂z₁
∂φ/∂ξ₀ = ∂φ/∂ξ₁ ∂φ/∂η₀ = ∂φ/∂η₁ ∂φ/∂ζ₀ = ∂φ/∂ζ₁
И то же самое для вторых производных:
∂²φ/∂x₀² = ∂²φ/∂x₁² ∂²φ/∂y₀² = ∂²φ/∂y₁² ∂²φ/∂z₀² = ∂²φ/∂z₁²
∂²φ/∂ξ₀² = ∂²φ/∂ξ₁² ∂²φ/∂η₀² = ∂²φ/∂η₁² ∂²φ/∂ζ₀² = ∂²φ/∂ζ₁²
С частной производной по времени несколько сложнее:
∂φ/∂t = ∂φ/∂ԏ - v₁₁(∂φ/∂x₁) - v₁₂(∂φ/∂y₁) - v₁₃(∂φ/∂z₁) - v₁₁(∂φ/∂ξ₁) - v₁₂(∂φ/∂η₁) - v₁₃(∂φ/∂ζ₁)
Я ранее уже писал, что поскольку x и ξ, y и η, z и ζ, t и ԏ всегда встречаются парами:
f = f(x - ξ, y - η, z - ζ, t - ԏ),
то нетрудно убедиться, что
Df = (∂f/∂x)(dx – dξ) + (∂f/∂y)(dy – dη) + (∂f/∂z)(dz – dζ) + (∂f/∂t)(dt – dԏ)
Хотя это очень просто, на всякий случай, я объясню, почему это так.
Допустим, у нас есть функция f от двух переменных p и s, причем в уравнении фигурирует именно их разность: f = f(p – s). Например, f = (p – s)³, или f = ln²(p – s), или f = sin²(p – s), и т.д.
Введем замену переменных: q = p – s. А теперь заметим, что частные производные ∂f/∂p и ∂f/∂s можно выразить через производную df/dq следующим образом:
∂f/∂p = (df/dq) (∂/∂p) (p – s) = df/dq
∂f/∂s = (df/dq) (∂/∂s) (p – s) = – df/dq
Что означает, в то же время, что
∂f/∂p = – ∂f/∂s
Итак, если мы запишем уравнение
∂φ/∂t = ∂φ/∂ԏ - v₁₁(∂φ/∂x₁) - v₁₂(∂φ/∂y₁) - v₁₃(∂φ/∂z₁) - v₁₁(∂φ/∂ξ₁) - v₁₂(∂φ/∂η₁) - v₁₃(∂φ/∂ζ₁)
как
∂φ/∂t = ∂φ/∂ԏ - v₁₁(∂φ/∂x₁ + ∂φ/∂ξ₁) - v₁₂(∂φ/∂y₁ + ∂φ/∂η₁) - v₁₃(∂φ/∂z₁ + ∂φ/∂ζ₁)
и произведем замены
∂φ/∂x₁ = – ∂φ/∂ξ₁
∂φ/∂y₁ = – ∂φ/∂η₁
∂φ/∂z₁ = – ∂φ/∂ζ₁
то это уравнение сокращается до
∂φ/∂t = ∂φ/∂ԏ
Далее, аналогично, легко получить
∂²φ/∂t² = ∂²φ/∂ԏ²
Что, собственно, и следовало ожидать, поскольку волновое уравнение, как и Второй Закон Ньютона, должно быть инвариантно относительно преобразований Галилея.
Здесь есть один нюанс. То, что сказано выше, относится к любой инерциальной системе отсчета – кроме системы отсчета движущегося источника. Потому что координаты (ξ₁, η₁, ζ₁) в этой системе отсчета равны нулю. Источник находится в начале координат и он, по определению, неподвижен. Это, в принципе, понятно и без всяких преобразований, но можно написать и их (в обозначениях Блохинцева):
ξ₀ = X(t)
η₀ = Y(t)
ζ₀ = Z(t)
x₁ = x₀ – X(t)
y₁ = y₀ – Y(t)
z₁ = z₀ – Z(t)
ξ₁ = ξ₀ – X(t) = 0
η₁ = η₀ – Y(t) = 0
ζ₁ = ζ₀ – Z(t) = 0
Как же так? В всех остальных системах отсчета, мы имели 6 пространственных координат, а в системе отсчета источника – только 3? Куда же делись эти пространственные координаты?
Главное различие между СО покоящейся среды и СО движущегося источника заключается в том, что в СО источника есть встречный ветер со скоростью –v₁ и с компонентами (–v₁₁, –v₁₂, –v₁₃), который сносит все волны. В двух словах, именно в этом ветре и «спрятались» наши исчезнувшие координаты (ξ₁, η₁, ζ₁). Число переменных остается тем же. Подробно разбирать этот вопрос я сейчас не хочу. Сначала нам надо будет получить «правильное» волновое уравнение (точнее, то, что я считаю правильным). Но до этого нам надо будет проделать еще длинный путь.
Можно, конечно, заметить, что в любой другой движущейся СО ветер тоже есть, но есть и координаты (ξ₁, η₁, ζ₁). Но это-то как раз не проблема. Это аналогично тому, что, в зависимости от выбора направлений осей координат, вы можете описать прямую линию в одномерном пространстве, двухмерном или трехмерном. «Лишние» переменные возникают всегда, если направления осей и т.п. выбраны не самым оптимальным образом.
Подведем некоторый итог. Я постарался показать, что сжатие в γ раз возникает из-за того, что, во-первых, вместо полной функции φ(x, y, z, ξ, η, ζ, t, ԏ) используется единичная функция φ(x, y, z, t). Во-вторых, переход из одной инерциальной системы отсчета в другую осуществляется неправильно: должен быть переход от координат (x₀, y₀, z₀, ξ₀, η₀, ζ₀) к (x₁, y₁, z₁, ξ₁, η₁, ζ₁), а не от (x, y, z) к (ξ, η, ζ).
Это не ошибки только Блохинцева – это заложено в фундаменте физики, «спрятано» в ее математическом аппарате. Точно те же ошибки привели в свое время к выводу преобразований Лоренца, которые, напомню, были получены в рамках классической физики, без всяких постулатов о постоянстве скорости света во всех инерциальных системах отсчета и прочих философских интерпретаций полученных формул.
Мы получили очень важный результат: мы увидели, что преобразования Лоренца не вытекают из постулата об ограничении скорости движения материальных тел скоростью света, не вытекают они даже и из уравнений Максвелла. Потому что совершенно аналогичные уравнения были получены Блохинцевым для звуковых волн, которые никак не связаны с электромагнетизмом, а их скорость в миллион раз меньше скорости света. Преобразования Лоренца и Блохинцева вытекают из одного источника – из самых основ математики физики.
Блохинцев, вероятно, честно проделал те же самые математические манипуляции, к которым он привык в электродинамике, теории относительности, квантовой механике, – и получил тот же самый результат. Он, впрочем, остановился в полушаге от замедления времени у движущегося источника, но да ладно, простим ему это. Nobody’s perfect.
Отредактировано: Yuri Rus - 21 ноя 2019 03:26:21

64 года
Карма: +394.08
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
А теперь я вам скажу очень странную вещь. Уравнения Блохинцева фундаментально, категорически неверны. Они не имеют никакого физического смысла. Но они ра-бо-та-ют.
Из Предисловия к книге:

Эти уравнения Блохинцева были реализованы «в железе», в комплексах для обнаружения вражеской авиации, которые использовались во время Великой Отечественной войны. В том, что наша страна победила, – заслуга в том числе и Д.И. Блохинцева, его уравнений. Вспомните также, что это было за время, какую ответственность нес Блохинцев за то, что его уравнения, его теория позволят войскам обнаружить и атаковать вражескую авиацию. В случае неуспеха, он отвечал головой. Цена ошибки здесь намного выше, чем для обычных физических экспериментов и теорий, не так ли? Но всё работало, причем с высокой точностью.
Уравнения Блохинцева, воплощенные «в железе», были, конечно, намного более сложными, чем те вводные уравнения, что процитировал я. Но они тоже включали в себя то самое сжатие в γ раз (например, для движущегося приемника звука). Если бы Блохинцев остановился сразу же, как только увидел сжатие в γ раз и подумал, что этого не может быть, это не имеет физического смысла, – он не смог бы создать теорию, позволяющую обнаруживать вражеские самолеты по генерируемому ими звуку. Потому что другой математики у него не было.
При этом, в книге Блохинцева встречаются такие высказывания, как:

Но понимание этого не помешало ему провести все математические манипуляции, все преобразования до логического конца – и принять те уравнения, которые получились.
Возникает, разумеется, вопрос: почему, если уравнения неверны, они приводят к правильным экспериментальным результатам? Как могут «работать» неверные уравнения?
Короткий ответ – потому что в реальных волнах действительно «сидит» γ, но она имеет совсем другой физический смысл, чем в уравнениях Блохинцева или в теории относительности. Сжатия в γ раз нет – есть искривление лучей и силовых линий, в котором фигурирует та самая γ. Длинный ответ будет позже – на то он и длинный, что займет много времени.
Здесь наиболее интересно следующее. Есть полная аналогия уравнений аэроакустики Блохинцева и теории относительности. При этом, мы видим, что уравнения Блохинцева, будучи неверными по своей физической сути, тем не менее, приводят к правильным результатам экспериментов и на их основе были построены и успешно использовались аппараты для обнаружения самолетов. Аналогично, очень похожие уравнения теории относительности приводят к правильным результатам экспериментов и на их основе были построены и успешно используются системы GPS и ГЛОНАСС, строятся Galileo и их китайский и индийский аналоги.
Так вот, я хочу подчеркнуть, что пример уравнений аэроакустики Блохинцева показывает, что успешное применение уравнений теории относительности на практике еще не доказывает, что эта теория верна, что она имеет физический смысл. Таким образом, практика не всегда является критерием истины. Экспериментальное подтверждение предсказаний теории еще не доказывает ее корректность. Как это ни грустно – потому что возникает вопрос: как же тогда отличать правильные теории от неправильных?
Я очень рад, что Блохинцев написал эту книгу. Если бы уравнений Блохинцева не было, мне пришлось бы их придумать, пришлось говорить, что ту же логику, что используется при анализе волновых уравнений электродинамики и приводит к преобразованиям Лоренца, можно применить и к уравнениям для звуковых волн, и мы получим точно такие же результаты, что не имеет физического смысла. Блохинцев проделал эти преобразования за меня и я ему очень признателен.
Из Предисловия к книге:

Эти уравнения Блохинцева были реализованы «в железе», в комплексах для обнаружения вражеской авиации, которые использовались во время Великой Отечественной войны. В том, что наша страна победила, – заслуга в том числе и Д.И. Блохинцева, его уравнений. Вспомните также, что это было за время, какую ответственность нес Блохинцев за то, что его уравнения, его теория позволят войскам обнаружить и атаковать вражескую авиацию. В случае неуспеха, он отвечал головой. Цена ошибки здесь намного выше, чем для обычных физических экспериментов и теорий, не так ли? Но всё работало, причем с высокой точностью.
Уравнения Блохинцева, воплощенные «в железе», были, конечно, намного более сложными, чем те вводные уравнения, что процитировал я. Но они тоже включали в себя то самое сжатие в γ раз (например, для движущегося приемника звука). Если бы Блохинцев остановился сразу же, как только увидел сжатие в γ раз и подумал, что этого не может быть, это не имеет физического смысла, – он не смог бы создать теорию, позволяющую обнаруживать вражеские самолеты по генерируемому ими звуку. Потому что другой математики у него не было.
При этом, в книге Блохинцева встречаются такие высказывания, как:

Но понимание этого не помешало ему провести все математические манипуляции, все преобразования до логического конца – и принять те уравнения, которые получились.
Возникает, разумеется, вопрос: почему, если уравнения неверны, они приводят к правильным экспериментальным результатам? Как могут «работать» неверные уравнения?
Короткий ответ – потому что в реальных волнах действительно «сидит» γ, но она имеет совсем другой физический смысл, чем в уравнениях Блохинцева или в теории относительности. Сжатия в γ раз нет – есть искривление лучей и силовых линий, в котором фигурирует та самая γ. Длинный ответ будет позже – на то он и длинный, что займет много времени.
Здесь наиболее интересно следующее. Есть полная аналогия уравнений аэроакустики Блохинцева и теории относительности. При этом, мы видим, что уравнения Блохинцева, будучи неверными по своей физической сути, тем не менее, приводят к правильным результатам экспериментов и на их основе были построены и успешно использовались аппараты для обнаружения самолетов. Аналогично, очень похожие уравнения теории относительности приводят к правильным результатам экспериментов и на их основе были построены и успешно используются системы GPS и ГЛОНАСС, строятся Galileo и их китайский и индийский аналоги.
Так вот, я хочу подчеркнуть, что пример уравнений аэроакустики Блохинцева показывает, что успешное применение уравнений теории относительности на практике еще не доказывает, что эта теория верна, что она имеет физический смысл. Таким образом, практика не всегда является критерием истины. Экспериментальное подтверждение предсказаний теории еще не доказывает ее корректность. Как это ни грустно – потому что возникает вопрос: как же тогда отличать правильные теории от неправильных?
Я очень рад, что Блохинцев написал эту книгу. Если бы уравнений Блохинцева не было, мне пришлось бы их придумать, пришлось говорить, что ту же логику, что используется при анализе волновых уравнений электродинамики и приводит к преобразованиям Лоренца, можно применить и к уравнениям для звуковых волн, и мы получим точно такие же результаты, что не имеет физического смысла. Блохинцев проделал эти преобразования за меня и я ему очень признателен.
Отредактировано: Yuri Rus - 21 ноя 2019 03:29:22
24 года
Карма: 0.00
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Цитата: Yuri Rus от 12.04.2011 09:08:35
Поехали!
Возможно, легче будет понять меня не действующим физикам (особенно преподавателям мат. физики или электродинамики), а «бывшим», скажем, выпускникам физтеха или физфака, которые в девяностые вынуждены были бросить науку, но физики по крайней мере не боятся и, открыв учебник, легко восстановят свои знания.
Поскольку я не ожидаю быстрого принятия моих идей от профессионального физического сообщества, я ориентируюсь на любителей физики, не владеющих слишком сложным математическим аппаратом. Писать я поэтому стараюсь очень просто, с подробными разъяснениями каждой детали. Понять меня сможет любой неглупый старшеклассник или первокурсник физической специальности (а не понять – профессиональные физики).
Желающим "бывшим" физикам востановить знания по векторным пространствам ссылкаhttp://eqworld.ipmnet.ru/ru/library/books/Sharipov2004ru.pdf
Пробежал взлядом ошибок не нашел.
Кстати вспомнил анекдот:
Энштейн умирает и попадает в рай.
При встрече с Богом он молит-" Господи ну покажи мне формулу мирозданья".
Господь улыбаясь дает ему расчеты - "все очень просто"...
Энштейн долго читает перечитывает-
"Господи но здесь же у тебя ОШИБКА!!!!"
Господь смотрит на помеченное Энштейном.
"...Да действительно ошибка, а я и не заметил......."

Отредактировано: Mikky Mouse - 03 май 2011 19:49:22
– Что такое электричество? – спросил однажды профессор студента.– Я знал, но забыл, – ответил студент. – Какая потеря для человечества! – воскликнул профессор. – Никто в мире не знает, что такое электричество. Один человек знал, и тот забыл! Когда вы вс
24 года
Карма: 0.00
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Пока научная общественность Авантюриста осмысливает заявления Юрия и не вступает в полемику делаю вывод- либо идея не понята либо процесс восстановления утраченных знаний затягивается.
Для ускорения процесса буду выкладывать и далее
( на мой взгляд) интересные ссылки.
Ацюковский Владимир Акимович (р. 16 июня 1930) — российский инженер, член РАЕН, профессор, доктор технических наук.теория эфира. http://www.atsuk.dart.ru/
его цитата
P.S. Есть прогресс. Начал по предложению Юрия искать ошибки в базисе.Пока нашел 1 - в Евклидовой геометрии.
Не хватает основной аксиомы.
Аксиома о точке. ТОЧКА это объект имеющий координаты . Точка это НОЛЬМЕРНОЕ пространство. Тогда возможно определение линии через две точки - это одномерное пространство. Плоскости через 3 точки -двухмерное пространсво и тогда N - мерное пространство определяется n-1 точкой.
Назвал в свою честь - Аксиома Mikky Mouse's (Smole Mouse's). Впервые публикую на авантюристе 07.05.2011.
ВСЕХ С ДНЕМ РАДИО!!!!
Для ускорения процесса буду выкладывать и далее
( на мой взгляд) интересные ссылки.
Ацюковский Владимир Акимович (р. 16 июня 1930) — российский инженер, член РАЕН, профессор, доктор технических наук.теория эфира. http://www.atsuk.dart.ru/
его цитата
Цитата
Обычно исследователи истории естествознания полагают, что по мере своего развития человечество накапливает знания. Это накопление связано, в частности, с выявлением законов природы и использованием их для нужд общества. Этот процесс несомненен. Однако в нем следует выделить этап закрепления знаний, связанный с их освоением общественным производст-вом. Только те знания имеют шанс сохраниться, которые нужны для данного способа производства, и при этом только тот период, пока этот существуют соответствующие технологии.
Если же уже имеющиеся знания не освоены как необходимый элемент технологии, то они остаются незамеченными, утрачива-ются, и в будущем, когда в них возникает необходимость, переоткрываются. А если соответствующая технология на определенном этапе развития оказывается вообще не нужной и она утрачивается, то вместе с ней утрачиваются и относящиеся к ней знания. Не навсегда, конечно, потому что, если вдруг возникнет необходимость, то они могут и переоткрыться.
P.S. Есть прогресс. Начал по предложению Юрия искать ошибки в базисе.Пока нашел 1 - в Евклидовой геометрии.
Не хватает основной аксиомы.
Аксиома о точке. ТОЧКА это объект имеющий координаты . Точка это НОЛЬМЕРНОЕ пространство. Тогда возможно определение линии через две точки - это одномерное пространство. Плоскости через 3 точки -двухмерное пространсво и тогда N - мерное пространство определяется n-1 точкой.
Назвал в свою честь - Аксиома Mikky Mouse's (Smole Mouse's). Впервые публикую на авантюристе 07.05.2011.
ВСЕХ С ДНЕМ РАДИО!!!!

Отредактировано: Mikky Mouse - 08 май 2011 01:17:07
– Что такое электричество? – спросил однажды профессор студента.– Я знал, но забыл, – ответил студент. – Какая потеря для человечества! – воскликнул профессор. – Никто в мире не знает, что такое электричество. Один человек знал, и тот забыл! Когда вы вс
24 года
Карма: 0.00
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Цитата: Yuri Rus
N+1 точкой?
да действительно обшибса.... :) Спасибо за уточнение.
– Что такое электричество? – спросил однажды профессор студента.– Я знал, но забыл, – ответил студент. – Какая потеря для человечества! – воскликнул профессор. – Никто в мире не знает, что такое электричество. Один человек знал, и тот забыл! Когда вы вс
24 года
Карма: 0.00
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Регистрация: 15.04.2011
Сообщений: 9
Читатели: 0
Цитата: Yuri Rus
N+1 точкой?
стыдно... опять не отстоял свое мнение... А все таки она вертится...
N мерное пространство определяется n-1 точкой... точка....
2 точки линия одномерное пространство с одномерными координатами...

– Что такое электричество? – спросил однажды профессор студента.– Я знал, но забыл, – ответил студент. – Какая потеря для человечества! – воскликнул профессор. – Никто в мире не знает, что такое электричество. Один человек знал, и тот забыл! Когда вы вс

64 года
Карма: +394.08
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Я уже говорил о том, как из неверного определения полной функции и полного дифференциала вытекает сжатие электрического поля движущегося заряда в γ раз. Затем я показал, как в акустике из-за неправильного перехода из одной инерциальной системы отсчета в другую возникает аналогичное сжатие звуковых волн в γ раз. На самом деле, я мог еще подчеркнуть, что сжатие в γ раз у Блохинцева возникает также потому, что он использовал неверное определение полной производной по времени. Но в том сообщении я хотел сделать фокус именно на переходе из одной инерциальной системы отсчета в другую, и не хотел распылять ваше внимание. Очень коротко упомяну об этом сейчас.
Напомню, как Блохинцев получил это сжатие:

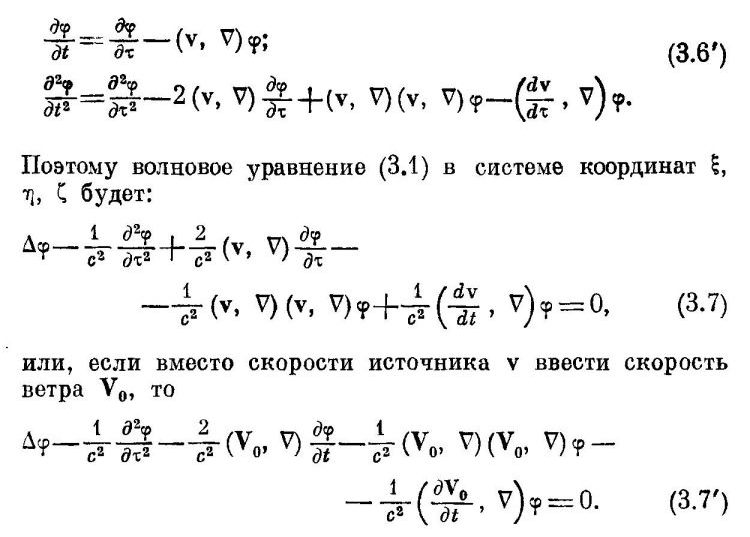
Посмотрим еще раз на первое из уравнений (3.6’):
∂φ/∂t = ∂φ/∂ԏ + (v, ∇)φ
В «раскрытом виде», это выглядит так:
∂φ/∂t = ∂φ/∂ԏ + (∂φ/∂ξ)(dξ/dԏ) + (∂φ/∂η)(dη/dԏ) + (∂φ/∂ζ)(dζ/dԏ)
Хотя это уравнение для частной производной φ по времени, заметим, что оно очень похоже на принятое в физике уравнение полной производной φ по времени:
dφ/dt = ∂φ/∂t + (v, ∇)φ = ∂φ/∂t + (∂φ/∂x)(dx/dt) + (∂φ/∂y)(dy/dt) + (∂φ/∂z)(dz/dt)
Только вместо (x, y, z, t) в уравнении (3.6') Блохинцев использует (ξ, η, ζ, ԏ).
В другом месте книги, Блохинцев для перехода из одной системы отсчета в другую использует именно полную производную по времени:
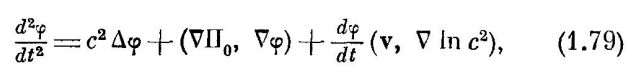


А что такое полная производная функции φ по времени, с точки зрения мат. физики? Это полный дифференциал dφ, разделенный на dt:
dφ = (∂φ/∂t)dt + (∂φ/∂x)dx + (∂φ/∂y)dy + (∂φ/∂z)dz
↓
dφ/dt = ∂φ/∂t + (∂φ/∂x)(dx/dt) + (∂φ/∂y)(dy/dt) + (∂φ/∂z)(dz/dt)
На самом деле, как я очень долго объяснял на первой странице данной ветки, dφ – это не полный дифференциал, а всего лишь единичный. Соответственно, второе уравнение – это уравнение не полной производной по времени, а единичной производной по времени. Мне не хочется все это опять повторять, поэтому я ограничусь ссылкой на первую страницу ветки.
Однако, эти мои аргументы вряд ли способны поколебать позиции теории относительности. Потому что преобразования Лоренца исторически были получены иным способом и в учебниках они вводятся совсем с других позиций, с другой аргументацией. В самом начале второй страницы, отвечая на вопрос Померонова, я привел цитату из книги Фейнмана, где как раз и выводились преобразования Лоренца тем самым способом, который использовал Лоренц (из потенциалов Льенара-Вихерта). Можно сказать, это то, с чего всё и началось (хотя первым эти преобразования получил Фитцджеральд на несколько лет раньше).
В следующих нескольких сообщениях я буду подробно разбирать, шаг за шагом, именно этот вывод преобразований Лоренца в пересказе Фейнмана. Это будет довольно большой текст, со множеством формул и рассуждений. Возможно, следить за логикой изложения будет нелегко, это потребует серьезной концентрации. Но если вы в глубине души допускаете, что сто, двести или триста лет назад где-то в основах физики могли быть допущены ошибки, если это для вас не закрытый вопрос, может быть, это стоит затраченных усилий?
Если же вы абсолютно, на 200 %, уверены, что никаких ошибок в основах физики нет, не было и не будет, читать вам, разумеется, незачем. Разве что, из спортивного интереса, чтобы уличить меня в моих ошибках и непонимании физики или математики. Что ж, и то хлеб. Возможно, кто-то из тех, кто начал меня читать с жгучим желанием уличить и посмеяться, в итоге задумается. Конструктивную критику я, кстати, всегда приветствую. Она помогает улучшить теорию или эксперимент.
Больше всего, я стремлюсь к простоте и ясности, особенно потому, что я ориентируюсь не на профессиональных физиков, а на более широкий круг читателей. Мне кажется, мои идеи будет легче понять, если я не вывалю сразу все детали за один раз, а буду идти от простого к сложному, шаг за шагом, используя метод последовательных приближений. В конце концов, именно так развивалась наука и так пишутся учебники.
Последовательные приближения означают, что те формулы, которые я даю в начале, на самом деле тоже неверны, они не учитывают очень важных моментов. Например, то самое нулевое приближение, о котором я уже говорил, предполагает, что каждая единичная волна распространяется по покоящейся среде (например, звуковые волны в жидкости). Первое приближение уже учитывает, что после прохождения первой же единичной волны среда приходит в движение и все последующие единичные волны распространяются по движущейся среде; волны взаимодействуют друг с другом, благодаря чему, кроме продольных, возникают поперечные волны. Второе приближение учитывает еще и то, что источник звука создает не только акустические волны, но он еще и «расталкивает» жидкость в стороны, приводя ее в движение (см. в учебниках «Движение сферы в жидкости»). Вот только здесь мы сможем перейти к построению теории электричества и магнетизма. Третье приближение учитывает еще взаимодействие поперечных волн. Это, наконец, и дает нам гравитацию.
Когда ранее я писал: «если мы хотим получить уравнения для гравитационного поля, мы не можем более пользоваться грубым «нулевым приближением», мы должны написать уравнения движения зарядов с точностью не менее чем 10⁻⁴²» – я имел в виду именно это. ДядяВася спросил меня, как я представляю себе опыт, для подтверждения правильности уравнения, с точностью до 47 знаков после запятой? Но опыт с такой точностью проводить нет никакой необходимости, потому что природа решила эту проблему за нас. Положительные и отрицательные заряды нейтрализуют друг друга с очень высокой точностью, так что на первый план выходят сначала намного более слабые магнитные поля, а затем, для астрономических объектов, еще более слабые гравитационные поля. Понимание того, как возникает гравитация, позволит, я надеюсь, генерировать искусственное гравитационное поле (при помощи электромагнитных устройств), которое по величине будет сравнимо с магнитным.
Далее, я говорил о том, что квантовая механика неверна и что никаких сильного и слабого взаимодействий не существует. Это, собственно, следует из совсем других соображений, из совсем другой моей теории, которая хронологически появилась намного раньше, чем все то, о чем я написал выше. Начинается она с анализа «стоячих волновых пакетов», потом использует полученные формулы для интерпретации Кулоновского поля и сил, действующих между частицами (частицы, впрочем, неотделимы от самого поля) на малых расстояниях. Оказывается, что поле это должно быть знакопеременным, что снимает необходимость предположения о дополнительных силах.
Это, так сказать, краткий план того, что же именно я собираюсь рассказать про физику в этой ветке на протяжении следующих месяцев. При этом, хочу подчеркнуть, что хотя я утверждаю, что физика неверна, потому что она использует неверную математику, я подхожу к этим проблемам отнюдь не как математик, а как физик. Физика, я полагаю, должна обладать безусловным приоритетом над математикой. Если математические манипуляции, сколь бы корректными они ни выглядели, приводят к бессмысленным с точки зрения физики выводам, следует искать ошибки в математике, а не в физике. Физика – это реальность. Математика – всего лишь модель реальности.
Конечная цель всех этих моих построений – открыть человечеству дорогу в Космос. Потому что только искусственная гравитация позволит нам достичь других звезд и галактик. Как раз сегодня arhivar-rus выложил очень интересные ссылки на видео и интерактивную карту звездного неба:
http://arhivar-rus.l…53060.html
Очень рекомендую – дает перспективу. И цель.
Напомню, как Блохинцев получил это сжатие:

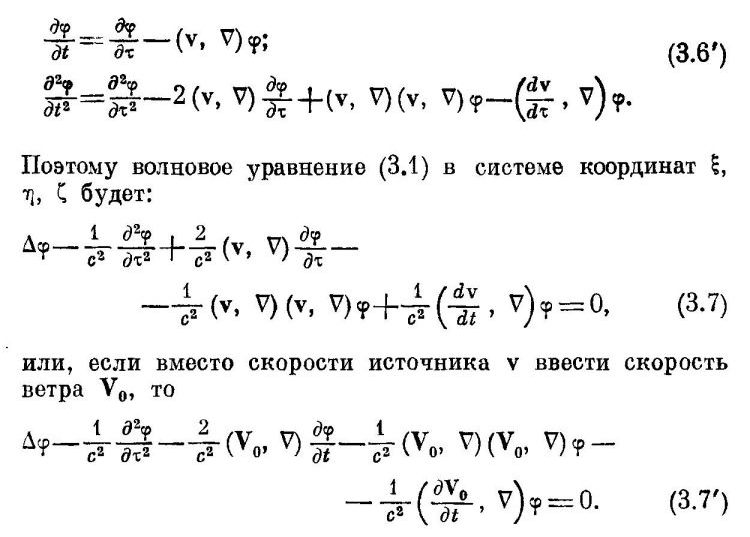
Посмотрим еще раз на первое из уравнений (3.6’):
∂φ/∂t = ∂φ/∂ԏ + (v, ∇)φ
В «раскрытом виде», это выглядит так:
∂φ/∂t = ∂φ/∂ԏ + (∂φ/∂ξ)(dξ/dԏ) + (∂φ/∂η)(dη/dԏ) + (∂φ/∂ζ)(dζ/dԏ)
Хотя это уравнение для частной производной φ по времени, заметим, что оно очень похоже на принятое в физике уравнение полной производной φ по времени:
dφ/dt = ∂φ/∂t + (v, ∇)φ = ∂φ/∂t + (∂φ/∂x)(dx/dt) + (∂φ/∂y)(dy/dt) + (∂φ/∂z)(dz/dt)
Только вместо (x, y, z, t) в уравнении (3.6') Блохинцев использует (ξ, η, ζ, ԏ).
В другом месте книги, Блохинцев для перехода из одной системы отсчета в другую использует именно полную производную по времени:
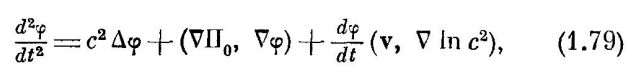


А что такое полная производная функции φ по времени, с точки зрения мат. физики? Это полный дифференциал dφ, разделенный на dt:
dφ = (∂φ/∂t)dt + (∂φ/∂x)dx + (∂φ/∂y)dy + (∂φ/∂z)dz
↓
dφ/dt = ∂φ/∂t + (∂φ/∂x)(dx/dt) + (∂φ/∂y)(dy/dt) + (∂φ/∂z)(dz/dt)
На самом деле, как я очень долго объяснял на первой странице данной ветки, dφ – это не полный дифференциал, а всего лишь единичный. Соответственно, второе уравнение – это уравнение не полной производной по времени, а единичной производной по времени. Мне не хочется все это опять повторять, поэтому я ограничусь ссылкой на первую страницу ветки.
Однако, эти мои аргументы вряд ли способны поколебать позиции теории относительности. Потому что преобразования Лоренца исторически были получены иным способом и в учебниках они вводятся совсем с других позиций, с другой аргументацией. В самом начале второй страницы, отвечая на вопрос Померонова, я привел цитату из книги Фейнмана, где как раз и выводились преобразования Лоренца тем самым способом, который использовал Лоренц (из потенциалов Льенара-Вихерта). Можно сказать, это то, с чего всё и началось (хотя первым эти преобразования получил Фитцджеральд на несколько лет раньше).
В следующих нескольких сообщениях я буду подробно разбирать, шаг за шагом, именно этот вывод преобразований Лоренца в пересказе Фейнмана. Это будет довольно большой текст, со множеством формул и рассуждений. Возможно, следить за логикой изложения будет нелегко, это потребует серьезной концентрации. Но если вы в глубине души допускаете, что сто, двести или триста лет назад где-то в основах физики могли быть допущены ошибки, если это для вас не закрытый вопрос, может быть, это стоит затраченных усилий?
Если же вы абсолютно, на 200 %, уверены, что никаких ошибок в основах физики нет, не было и не будет, читать вам, разумеется, незачем. Разве что, из спортивного интереса, чтобы уличить меня в моих ошибках и непонимании физики или математики. Что ж, и то хлеб. Возможно, кто-то из тех, кто начал меня читать с жгучим желанием уличить и посмеяться, в итоге задумается. Конструктивную критику я, кстати, всегда приветствую. Она помогает улучшить теорию или эксперимент.
Больше всего, я стремлюсь к простоте и ясности, особенно потому, что я ориентируюсь не на профессиональных физиков, а на более широкий круг читателей. Мне кажется, мои идеи будет легче понять, если я не вывалю сразу все детали за один раз, а буду идти от простого к сложному, шаг за шагом, используя метод последовательных приближений. В конце концов, именно так развивалась наука и так пишутся учебники.
Последовательные приближения означают, что те формулы, которые я даю в начале, на самом деле тоже неверны, они не учитывают очень важных моментов. Например, то самое нулевое приближение, о котором я уже говорил, предполагает, что каждая единичная волна распространяется по покоящейся среде (например, звуковые волны в жидкости). Первое приближение уже учитывает, что после прохождения первой же единичной волны среда приходит в движение и все последующие единичные волны распространяются по движущейся среде; волны взаимодействуют друг с другом, благодаря чему, кроме продольных, возникают поперечные волны. Второе приближение учитывает еще и то, что источник звука создает не только акустические волны, но он еще и «расталкивает» жидкость в стороны, приводя ее в движение (см. в учебниках «Движение сферы в жидкости»). Вот только здесь мы сможем перейти к построению теории электричества и магнетизма. Третье приближение учитывает еще взаимодействие поперечных волн. Это, наконец, и дает нам гравитацию.
Когда ранее я писал: «если мы хотим получить уравнения для гравитационного поля, мы не можем более пользоваться грубым «нулевым приближением», мы должны написать уравнения движения зарядов с точностью не менее чем 10⁻⁴²» – я имел в виду именно это. ДядяВася спросил меня, как я представляю себе опыт, для подтверждения правильности уравнения, с точностью до 47 знаков после запятой? Но опыт с такой точностью проводить нет никакой необходимости, потому что природа решила эту проблему за нас. Положительные и отрицательные заряды нейтрализуют друг друга с очень высокой точностью, так что на первый план выходят сначала намного более слабые магнитные поля, а затем, для астрономических объектов, еще более слабые гравитационные поля. Понимание того, как возникает гравитация, позволит, я надеюсь, генерировать искусственное гравитационное поле (при помощи электромагнитных устройств), которое по величине будет сравнимо с магнитным.
Далее, я говорил о том, что квантовая механика неверна и что никаких сильного и слабого взаимодействий не существует. Это, собственно, следует из совсем других соображений, из совсем другой моей теории, которая хронологически появилась намного раньше, чем все то, о чем я написал выше. Начинается она с анализа «стоячих волновых пакетов», потом использует полученные формулы для интерпретации Кулоновского поля и сил, действующих между частицами (частицы, впрочем, неотделимы от самого поля) на малых расстояниях. Оказывается, что поле это должно быть знакопеременным, что снимает необходимость предположения о дополнительных силах.
Это, так сказать, краткий план того, что же именно я собираюсь рассказать про физику в этой ветке на протяжении следующих месяцев. При этом, хочу подчеркнуть, что хотя я утверждаю, что физика неверна, потому что она использует неверную математику, я подхожу к этим проблемам отнюдь не как математик, а как физик. Физика, я полагаю, должна обладать безусловным приоритетом над математикой. Если математические манипуляции, сколь бы корректными они ни выглядели, приводят к бессмысленным с точки зрения физики выводам, следует искать ошибки в математике, а не в физике. Физика – это реальность. Математика – всего лишь модель реальности.
Конечная цель всех этих моих построений – открыть человечеству дорогу в Космос. Потому что только искусственная гравитация позволит нам достичь других звезд и галактик. Как раз сегодня arhivar-rus выложил очень интересные ссылки на видео и интерактивную карту звездного неба:
http://arhivar-rus.l…53060.html
Очень рекомендую – дает перспективу. И цель.
Отредактировано: Yuri Rus - 21 ноя 2019 03:47:12
Карма: +147.41
Регистрация: 05.06.2010
Сообщений: 19,882
Читатели: 8
Регистрация: 05.06.2010
Сообщений: 19,882
Читатели: 8
Цитата: Yuri Rus от 10.05.2011 18:44:14
<skip>
Посмотрим еще раз на первое из уравнений (3.6’):
∂φ/∂t = ∂φ/∂ԏ + (v, ∇)φ
У Блохинцева вроде - ( минус ).
Цитата: Yuri Rus от 10.05.2011 18:44:14
В «раскрытом виде», это выглядит так:
∂φ/∂t = ∂φ/∂ԏ + (∂φ/∂ξ)(dξ/dԏ) + (∂φ/∂η)(dη/dԏ) + (∂φ/∂ζ)(dζ/dԏ)
Хотя это уравнение для частной производной φ по времени, заметим, что оно очень похоже на принятое в физике уравнение полной производной φ по времени:
dφ/dt = ∂φ/∂t + (v, ∇)φ = ∂φ/∂t + (∂φ/∂x)(dx/dt) + (∂φ/∂y)(dy/dt) + (∂φ/∂z)(dz/dt)
Соответственно здесь тоже минус и соответственно не "очень похоже".

64 года
Карма: +394.08
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: Поверонов от 10.05.2011 22:39:02
У Блохинцева вроде - ( минус ).
Соответственно здесь тоже минус и соответственно не "очень похоже".
Да, минус я не заметил. Когда я читал книгу, я больше внимания уделял первому переходу из одной СО в другую (у Блохинцева уравнения (1.79) и (1.85)-(1.86) расположены, разумеется, раньше, чем уравнения (3.5)-(3.7)), и не обратил внимания на то, что во втором случае появляется минус. Впрочем, частная производная в любом случае это не полная производная по времени, так что аргумент этот был косвенным и не принципиальным. Хорошо, вычеркнем его.
59 лет
Карма: +173.90
Регистрация: 20.09.2008
Сообщений: 15,652
Читатели: 11
Регистрация: 20.09.2008
Сообщений: 15,652
Читатели: 11
Цитата: Yuri Rus от 12.04.2011 09:20:01
... Назовем такую функцию y(x, u) в трехмерном пространстве полной функцией (full, or total function), а индивидуальные функции y(x, u) в двухмерном пространстве – единичными функциями (singular functions). (((Вопрос к аудитории: какой термин лучше – единичная функция или индивидуальная функция?))) ...
partial
аналогично терминам - давление, парциальное давление
И при анализе уравнений с параметрами всегда принимается (аксиома!), что параметр это константа, т.е. ∂u = du = 0;
Если параметр не константа, то он считается переменной, на уровне формализма добавляется в список параметров (как Вы и сделали) и далее "как всегда".
По сути Вам не нужно вводить новые сущности (единичный дифференциал соответствует классическому частному дифференциалу в задаче большей размерности (там, где параметр стал переменной)).
То что уже прочитал - вы не опровергаете Матфизику, но меняете постановку задачи (что можно только приветствовать!!!), делая следующее приближение.
Под "следующим приближением" имеется в виду, например, такой ряд задач:
1. Просто неподвижный заряд
2. Заряд "сдвинувшийся на совсем мало" (неподвижный "источник волны")
3. Равномерно медленно движущийся заряд
4. Равномерно медленно движущийся "источник волны"
5. и т.д.
Поэтому естественно то, что при одном приближени было параметром (т.е. константой) при другом становится переменной.
Однородное волновое уравнение описывает распространение невзаимодействующих волн (линейная суперпозиция т.е. амплитуда волны считается бесконечно малой) в среде без источноков.
Отредактировано: BUR - 21 май 2011 03:19:27
Толерантность - термин, означающий невозможность организма распознавать инородные клетки.
Западная борьба с коррупцией в России - борьба за легальную куплю-продажу власти иностранными агентами.
Честность, Справедливость, Состоятельность
Западная борьба с коррупцией в России - борьба за легальную куплю-продажу власти иностранными агентами.
Честность, Справедливость, Состоятельность

Карма: +2.39
Регистрация: 26.10.2008
Сообщений: 1,229
Читатели: 3
Регистрация: 26.10.2008
Сообщений: 1,229
Читатели: 3
Не могу не согласиться с Поверонов, что физика есть суть упрощение, модель реальности, более или менее адекватно пытающуюся описать эту реальность, дабы суметь предсказать поведение оной, согласно нарисованной модели и, соответственно, попользоваться полезным эффектом. И говорить, что в описаниях модели содержаться ошибки,т.к. она несколько неверно описывает реальность, по крайней мере, абсурдно. Само понятие модель и предполагает, что мы преднамеренно упростили реальность, введя некоторые абстрактные понятия, как то: сила, энергия, импульс, волна и т.п. ,(которых в реальности нет, как правильно писал mozgi, есть только возмущения и взаимодействия).
По мере развития, модели уточняются, достигают некоторого предельного уровня, когда пора вводит новый уровень абстракций, старая модель (зарекомедовавшая себя на протяжении веков, а значит на этом уровне приближения абстракции верно описывающая реальность) отнюдь не отбрасывается, а просто становится частным случаем модели более высокого уровня.
Так что громкое заявление «что одной из важнейших внутренних причин грядущей катастрофы является глубокая ошибочность современной физики» ,каГбы наводит на определеные мысли, самая безобидная из которых, что вы не понимаете суть, философию развития жизни. Если бы Вы предложили качественно новую, более высшую ступень абстракции (например, как эту, куда все современное здание науки войдет частным случаем, при определенных допущениях, то честь Вам и хвала, а так ,увы,Вы пытаетесь одну модель современного здания науки, которая уже зарекомендовала себя реальными результатами, заменить своей моделью, у которой лишь громкие заявления. Не более.
Непонятен так же смысл «простыней» на сугубо политико-экономическом форуме, ведь в сети полно чисто физических форумов, где, я думаю, найдутся истинные физики, понимающие досконально не только сами эти формулы, но и то, что это лишь суть абстракции, допущения, математические модели и искать в них ошибки, тоже самое, что возмущаться, почему облака не правильные конусы и элипсы, хотя формулы говорят, что они должны быть такими . И даже сугубо по теории относительности полно форумов, где все эти парадоксы масс и близнецов постоянно жуются. Вот и выложите там свое откровение: "Я считаю, что теория относительности неверна...Теория относительности постулирует, что движение быстрее скорости света невозможно и что по мере приближения скорости космического корабля к скорости света его масса будет стремиться к бесконечности», может найдутся понимающие люди, которые объяснят Вам, что теория относительности, постулирующая бесконечность массы при световой скорости это одно, а реальность несколько иное, и в ней ни какой бесконечной массы не будет, и ниспровергать основ физики Вам не придеться.
. И даже сугубо по теории относительности полно форумов, где все эти парадоксы масс и близнецов постоянно жуются. Вот и выложите там свое откровение: "Я считаю, что теория относительности неверна...Теория относительности постулирует, что движение быстрее скорости света невозможно и что по мере приближения скорости космического корабля к скорости света его масса будет стремиться к бесконечности», может найдутся понимающие люди, которые объяснят Вам, что теория относительности, постулирующая бесконечность массы при световой скорости это одно, а реальность несколько иное, и в ней ни какой бесконечной массы не будет, и ниспровергать основ физики Вам не придеться.
И что у Вас, так все утилитарно: :)"Ресурсы сначала Солнечной системы, затем других звездных систем будут доступны людям – и перевозка тяжелых грузов (металлов и пр. ) от дальних звезд будет вполне рентабельна», возить, ресурсы, что бы делать очередной виток потреблятсва. А как насчет психофизического посещения других планет, без всяких полетов громоздких железок, посредством тонкой субстанции человека. Как насчет развития по пути не роста потреблятсва, все увеличивающегося населения, а как осознанная жизнь в согласии с природой и космосом.
) от дальних звезд будет вполне рентабельна», возить, ресурсы, что бы делать очередной виток потреблятсва. А как насчет психофизического посещения других планет, без всяких полетов громоздких железок, посредством тонкой субстанции человека. Как насчет развития по пути не роста потреблятсва, все увеличивающегося населения, а как осознанная жизнь в согласии с природой и космосом.
По мере развития, модели уточняются, достигают некоторого предельного уровня, когда пора вводит новый уровень абстракций, старая модель (зарекомедовавшая себя на протяжении веков, а значит на этом уровне приближения абстракции верно описывающая реальность) отнюдь не отбрасывается, а просто становится частным случаем модели более высокого уровня.
Так что громкое заявление «что одной из важнейших внутренних причин грядущей катастрофы является глубокая ошибочность современной физики» ,каГбы наводит на определеные мысли, самая безобидная из которых, что вы не понимаете суть, философию развития жизни. Если бы Вы предложили качественно новую, более высшую ступень абстракции (например, как эту, куда все современное здание науки войдет частным случаем, при определенных допущениях, то честь Вам и хвала, а так ,увы,Вы пытаетесь одну модель современного здания науки, которая уже зарекомендовала себя реальными результатами, заменить своей моделью, у которой лишь громкие заявления. Не более.
Непонятен так же смысл «простыней» на сугубо политико-экономическом форуме, ведь в сети полно чисто физических форумов, где, я думаю, найдутся истинные физики, понимающие досконально не только сами эти формулы, но и то, что это лишь суть абстракции, допущения, математические модели и искать в них ошибки, тоже самое, что возмущаться, почему облака не правильные конусы и элипсы, хотя формулы говорят, что они должны быть такими
 . И даже сугубо по теории относительности полно форумов, где все эти парадоксы масс и близнецов постоянно жуются. Вот и выложите там свое откровение: "Я считаю, что теория относительности неверна...Теория относительности постулирует, что движение быстрее скорости света невозможно и что по мере приближения скорости космического корабля к скорости света его масса будет стремиться к бесконечности», может найдутся понимающие люди, которые объяснят Вам, что теория относительности, постулирующая бесконечность массы при световой скорости это одно, а реальность несколько иное, и в ней ни какой бесконечной массы не будет, и ниспровергать основ физики Вам не придеться.
. И даже сугубо по теории относительности полно форумов, где все эти парадоксы масс и близнецов постоянно жуются. Вот и выложите там свое откровение: "Я считаю, что теория относительности неверна...Теория относительности постулирует, что движение быстрее скорости света невозможно и что по мере приближения скорости космического корабля к скорости света его масса будет стремиться к бесконечности», может найдутся понимающие люди, которые объяснят Вам, что теория относительности, постулирующая бесконечность массы при световой скорости это одно, а реальность несколько иное, и в ней ни какой бесконечной массы не будет, и ниспровергать основ физики Вам не придеться.И что у Вас, так все утилитарно: :)"Ресурсы сначала Солнечной системы, затем других звездных систем будут доступны людям – и перевозка тяжелых грузов (металлов и пр.
 ) от дальних звезд будет вполне рентабельна», возить, ресурсы, что бы делать очередной виток потреблятсва. А как насчет психофизического посещения других планет, без всяких полетов громоздких железок, посредством тонкой субстанции человека. Как насчет развития по пути не роста потреблятсва, все увеличивающегося населения, а как осознанная жизнь в согласии с природой и космосом.
) от дальних звезд будет вполне рентабельна», возить, ресурсы, что бы делать очередной виток потреблятсва. А как насчет психофизического посещения других планет, без всяких полетов громоздких железок, посредством тонкой субстанции человека. Как насчет развития по пути не роста потреблятсва, все увеличивающегося населения, а как осознанная жизнь в согласии с природой и космосом.
Отредактировано: wow - 21 май 2011 15:19:50
Карма: +147.41
Регистрация: 05.06.2010
Сообщений: 19,882
Читатели: 8
Регистрация: 05.06.2010
Сообщений: 19,882
Читатели: 8
Цитата: Yuri Rus
К сожалению, термин занят. Пусть не для функций, но для производной и дифференциала. А поскольку ниже я ввожу аналогичный термин для дифференциала, то ради единообразия терминов я не могу использовать "частную" (partial) функцию. Я об этом упомянул.
Коль о терминах возникла речь. Обычно уменьшение размерности путем "замораживания" значения одной или нескольких переменных называют "проекцией" на подпространство. Назовите эти свои функции "проективными" или просто проекциями, если это не внесет путаницы в последующем изложении.
59 лет
Карма: +173.90
Регистрация: 20.09.2008
Сообщений: 15,652
Читатели: 11
Регистрация: 20.09.2008
Сообщений: 15,652
Читатели: 11
Цитата: wow от 21.05.2011 12:36:07
... все современное здание науки войдет частным случаем, при определенных допущениях, то честь Вам и хвала, а так ,увы,Вы пытаетесь одну модель современного здания науки, которая уже зарекомендовала себя реальными результатами, заменить своей моделью, у которой лишь громкие заявления. Не более. ...
Процитированное, вообще говоря, неверно. Вспомните конец 19 века. Теория флогистона (теплорода) работает, дает практические результаты (уравнение теплопроводности). И тут появляется некто и говорит - флогистона нет, есть внутренняя энергия, а ему в ответ Ваш аргумент.
По сути вся современная физика в той или иной степени феноменологична, т.е. в качестве "практического результата" дает математическую модель определенных явлений. Одни и те-же математические модели могут получаться из различных обоснований, например серия Ридберга в спектре водорода получается и при различных построениях модели автома водорода, но эти модели с разной степенью точности "обламываются" уже на атоме гелия. Или уже упомянутое уравнение теплопроводности.
Насчет "увеличения массы при приближении к скорости цвета" в СТО - всё упирается в определение массы (например "масса это коэффициент связывающий ускорение и активную силу в данной среде"). В случае плотной среды (не вакуум) получится, что находясь внутри среды мы использя активную силу (опираясь на среду) не можем разогнать тело до скорости, превышающей скорость взаимодействия в среде. Но мы из физических экспериментов знаем, что частица может двигаться в плотной среде быстрее скорости света (теряя энергию в виде черенковского излучения), но опять-же находясь в плотной среде мы разогнать частицу опираясь на среду до скорости света в среде не можем - будем наблюдать бесконечный рост "массы" (как коэффициента связывающего ускорение и силу) по мере приближения скорости к скорости взаимодействия в среде.
Но в то-же время мы знаем (движение на реактивной тяге в воздухе со сверхзвуковой скоростью), что превысить скорость взаимодействия в среде возможно, если есть запас внутренней энергии (в случае ракеты в виде топлива) и реактивный способ движения (отталкиваемся не от среды, а от кусочка себя). Будет ли (в случеа вакуума) расти до бесконечности масса по мере приближения к скорости взаимодействия в среде, если определить "масса это коэффициент, связывающий реактивную силу с ускорением в данной среде"?
Можно-ли такую формулировку расширить с движения тела с реактивной тягой в плотной среде на движение в вакууме? Как выглядит движение сверхзвукового самолета с точки зрения "наблюдателя" регистрирующего движения только посредством микрофонов? Можно-ли это проверить экспериментально (например наблюдая распад движущейся с субсветовой скоростью частицы и интерпретируя фотоны как черенковское излучение)? На таком уровне рассмотрения мне образования уже не хватает, чтобы сделать осмысленные оценки...
Отредактировано: BUR - 21 май 2011 14:43:08
Толерантность - термин, означающий невозможность организма распознавать инородные клетки.
Западная борьба с коррупцией в России - борьба за легальную куплю-продажу власти иностранными агентами.
Честность, Справедливость, Состоятельность
Западная борьба с коррупцией в России - борьба за легальную куплю-продажу власти иностранными агентами.
Честность, Справедливость, Состоятельность

Карма: +2.39
Регистрация: 26.10.2008
Сообщений: 1,229
Читатели: 3
Регистрация: 26.10.2008
Сообщений: 1,229
Читатели: 3
Цитата: BUR от 21.05.2011 14:26:04
Процитированное, вообще говоря, неверно. Вспомните конец 19 века. Теория флогистона (теплорода) работает, дает практические результаты (уравнение теплопроводности). И тут появляется некто и говорит - флогистона нет, есть внутренняя энергия, а ему в ответ Ваш аргумент.
Хмм..., видно из-за краткости, я не совсем удачно выразился. Я как раз это и хотел сказать, даже привести теорию флогистона
 . Ведь реально формулы остались и перетекли в теплотехнику, значит на этом уровне допущения абстракции реальности, правильно описали эту реальность.
. Ведь реально формулы остались и перетекли в теплотехнику, значит на этом уровне допущения абстракции реальности, правильно описали эту реальность.А как назвать это - флогистон, энергия, некая "вечная субстанция" , это уже уровень абстракции, на который мы по мере развития поднялись, и который более точно описывает реальность. Энергии, как и флогистона, ведь тоже нет. Есть просто абстрактное понятие, коим мы пытаемся более полно, чем флогистон описать некие процессы по передачи НЕЧТО от одного тела к другому, описать некоторые феномены взаимодействия тел. И ваше понятие массы абсолютно верно: в физике это просто коэфициент, ну может еще колличество НЕЧТО, что мы называем вещество. И основная мысль моя -это настороженно относиться ко всем ниспровергателям основ. Что ниспровергать? Свой путь развития? Те абстракции, которые развиваются от простого к сложному, на пути более полного описания реальности?
Отредактировано: wow - 21 май 2011 15:10:33

moscow
Карма: +788.72
Регистрация: 09.01.2011
Сообщений: 12,560
Читатели: 11
Регистрация: 09.01.2011
Сообщений: 12,560
Читатели: 11
Цитата: wow от 21.05.2011 12:36:07
Если бы Вы предложили качественно новую, более высшую ступень абстракции (например, как эту, куда все современное здание науки войдет частным случаем...
Спасибо за любопытную ссылку. Сейчас действительно вошло в моду "квантование" ВСЕГО. Чего только не пишут и о "квантовом" сознании, и о "квантовой" логике просто квантомания какая-то. Похоже замещение столь же популярного в своё время термина Атом/атомный уже окончательно свершилось.
При этом это далеко не каждый конечно может оценить красоту полета фантазии авторов (я обычно классифицирую подобные писания как пси-триллер, жанр Sci-Fi) в поисках Теории Всего, особенно с претензией на "более высшую ступень абстракции"(с), куда им грезится по ходу дела засунуть "все современное здание науки" :)
Вроде, не сильно заметно, тем более в научно-техническом разделе желающих по прочтении "ниспровергателей основ" совершать какие-то малоадекватные социальные действия. ;)
Тем более, что вопросы поднимаемые автором топика стоят на повестке дня весьма давно и по теме имеется большое количество точек зрения, не согласующихся с рядом положений, которые порой носят уже порой ярко выраженный характер догмата, а не гипотетического (пусть сильного ) допущения, которым и является фактически любая современная пусть и общепринятая теория в любом разделе науки (фальсифицируемость).
Кстати, в истории науки далеко не всегда происходит вхождение частным случаем в более общее. Поинтересуйтесь у астрономов что сталось с эпициклами птолемеевской небесной механики, и применяются ли довольно изощрённые для своего времени формулы расчёта нахождения небесных тел на небосклоне (довольно точные) с использованием таблиц эпициклов в наше время (вроде только в астрологии).
ЗЫ. Ув. Yuri Rus ждем продолжения. Термин предложенный Повероновым "проективный" ( projective ) вполне можно рассмотреть.
Народ безмолвствует. А счастлив ли Народ?...
Карма: +147.41
Регистрация: 05.06.2010
Сообщений: 19,882
Читатели: 8
Регистрация: 05.06.2010
Сообщений: 19,882
Читатели: 8
Цитата: wow от 21.05.2011 15:06:11
<skip>
И основная мысль моя -это настороженно относиться ко всем ниспровергателям основ. Что ниспровергать? Свой путь развития? Те абстракции, которые развиваются от простого к сложному, на пути более полного описания реальности?
Основа физики - данные экспериментов. И в этом отношении ничего опровергнуть невозможно, что померяно - то и есть, ну разве что были ошибочные измерения, так это быстро выявляется и опровергается.
А вот интерпретации экспериментальных данных - это неисчерпаемое поле творчества и спекуляций. В принципе всякая теория, дающая те же расчетные значения, что и проверенные экспериментально, ничем не хуже общепринятой, а может быть и лучше, если дает интересные и полезные следствия.

64 года
Карма: +394.08
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: Поверонов от 21.05.2011 13:31:09
Коль о терминах возникла речь. Обычно уменьшение размерности путем "замораживания" значения одной или нескольких переменных называют "проекцией" на подпространство. Назовите эти свои функции "проективными" или просто проекциями, если это не внесет путаницы в последующем изложении.
Я, конечно, тоже встречал термин "проекция" и, наверно, с точки зрения математики он вполне корректен. Но в данном случае, использование терминов "проективная функция", "проективный дифференциал", "проективная волна" все же режет слух и глаз. Особенно для волны, как-то слово "проекция" вызывает совсем другие ассоциации.

64 года
Карма: +394.08
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: BUR от 21.05.2011 02:05:32
И при анализе уравнений с параметрами всегда принимается (аксиома!), что параметр это константа, т.е. ∂u = du = 0;
Если параметр не константа, то он считается переменной, на уровне формализма добавляется в список параметров (как Вы и сделали) и далее "как всегда".
По сути Вам не нужно вводить новые сущности (единичный дифференциал соответствует классическому частному дифференциалу в задаче большей размерности (там, где параметр стал переменной)).
То что уже прочитал - вы не опровергаете Матфизику, но меняете постановку задачи (что можно только приветствовать!!!), делая следующее приближение.
Я бы рад не вводить новые сущности, но ведь учебники-то по физике пока не переписали, а потому мне надо как-то объяснить разницу между принятым в физике понятием полного дифференциала и более общим понятием, которое я ввожу. А введение специального термина часто единственный путь к краткости, иначе вместо одного слова каждый раз придется давать его полное определение.
Далее - я не опровергаю математику. Но пытаюсь показать, что многие принятые в мат. физике понятия и формулы неверны. Дело в том, что мат. физика имеет блочную структуру. Однажды выведенная формула, после первого периода критики и экспериментальной проверки, становится "блоком", кирпичом в строительстве следующих этажей физики. В дальнейшем, эта формула просто считается истинной и ее применяют для вывода каких-то других формул, более не подвергая ее саму сомнению. Примеры: Второй Закон Ньютона, Второй Закон Термодинамики и Принцип Неопределености Гейзенберга. Их просто применяют, как инструменты решения каких-то новых физических задач, почти никогда не ставя вопрос о том, справедливы ли сами эти законы и если да, то в какой области параметров.
Я пытаюсь показать, что на довольно раннем этапе развития физики при создании некоторых ключевых блоков были допущены ошибки. Математика-то в целом верна, но ее применение к созданию определенных физических моделей было неверным. Поскольку этого никто не заметил в первый, "критический" период жизни этих моделей, в последующие уже даже не десятилетия, а столетия, эти модели, эти формулы вошли в виде блоков во все остальное здание мат. физики. И здание это, в итоге, стоит на очень шатком основании.
Чтобы распутать этот детектив, я и начал с анализа единичных vs. полных функций, дифференциалов и волн. Особую роль, по моему мнению, сыграли ошибки в анализе линейного неоднородного волнового уравнения с движущимся источником. Поэтому я уделяю этому уравнению основное внимание.
Цитата: BUR от 21.05.2011 02:05:32
Под "следующим приближением" имеется в виду, например, такой ряд задач:
1. Просто неподвижный заряд
2. Заряд "сдвинувшийся на совсем мало" (неподвижный "источник волны")
3. Равномерно медленно движущийся заряд
4. Равномерно медленно движущийся "источник волны"
5. и т.д.
Поэтому естественно то, что при одном приближени было параметром (т.е. константой) при другом становится переменной.
Однородное волновое уравнение описывает распространение невзаимодействующих волн (линейная суперпозиция т.е. амплитуда волны считается бесконечно малой) в среде без источноков.
Всё верно - принцип суперпозиции выполняется только для линейного однородного волнового уравнения. Но не для неоднородного - и в особенности он не выполняется для движущегося источника. Это как раз я и считаю главной ошибкой мат. физики.
Сейчас на ветке:
1,
Модераторов: 0,
Пользователей: 0,
Гостей: 0,
Ботов: 1