Жизнь, Разум, Человек, Религия и Наука
152.5 K
201
565

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Но вывод уравнения Лиенара-Вихерта, тем не менее, неверен. Никакого множителя вида 1 / (1 – r’∙v / (r’ c)) при движении зарядов или источников звука не появляется. В сообщении, где я анализировал вывод уравнения Лиенара-Вихерта, это было сделано именно что качественно, на пальцах. Упрощать далее довольно трудно. Разве что могу выделить наиболее важный кусочек и изложить его слегка иначе.
Итак, задача формулируется следующим образом. Мы хотим знать, чему равен потенциал от движущегося заряда в момент времени t в покоящейся точке P. Это делается при помощи интеграла по объему от плотности заряда и расстояния до заряда в момент излучения сигнала:
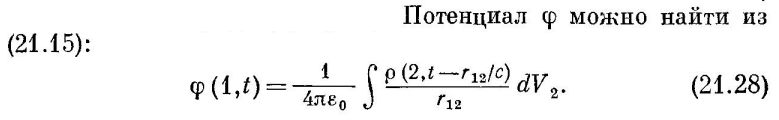
Поскольку заряд движется, то для того, чтобы достичь точки Р одновременно, сигналы от разных частей заряда должны быть излучены в разные моменты времени. Чем дальше от точки Р находится какой-то элемент заряда, тем раньше должен быть излучен сигнал от него. Причем за то время, пока сигнал от самого дальнего элемента заряда дойдет до самого ближнего элемента, этот ближний элемент успеет пройти какое-то расстояние.
Уравнения динамики записываются обычно в 2 формах - лагранжевой и эйлеровой. Уравнения в форме Лагранжа описывают движения индивидуальной частицы жидкости или твердого тела. Уравнения в форме Эйлера описывают то, что происходит в некотором элементе объема пространства. Рассматриваются силы, скорости, смещения и т.д. применительно именно к этому малому элементу пространства; судьба индивидуальных частиц при этом не важна. На примере реки: Лагранж интересуется движением индивидуальных частиц жидкости, а Эйлер – скоростями и пр. в определенной точке пространства, где одни частицы постоянно сменяются другими.
Задача определения потенциала от движущегося заряда является ярким примером подхода Эйлера. Решается она так:
Для простоты, будем считать, что заряд имеет кубическую форму и точка Р находится прямо по направлению движения заряда, на оси движения. Объем пространства, через который пройдет заряд за то время, пока сигнал от самого дальнего от точки Р элемента заряда путешествовал до самого ближнего элемента, разбивается на элементы толщиной w. Суммарный потенциал в точке Р определяется как сумма сигналов от каждого элемента объема, излученных в последовательные моменты времени (разница между которыми dt = w/c). Подчеркиваю – от каждого элемента объема, а не элемента заряда. Допустим, для примера, что скорость источника v = 0.75 c. Процедура суммирования сигналов такова:
Сначала к сумме добавляется сигнал от самого дальнего элемента объема, где в этот момент находится первый элемент заряда с толщиной w и плотностью заряда ρ. Потом мы переходим к следующему элементу объема толщиной w и добавляем к сумме его сигнал, излученный в момент времени dt = w/c. За это время, первый элемент заряда успел частично сместиться во второй элемент объема, так что 75% второго элемента объема будут заполнены первым элементом заряда – и он опять вносит вклад в сигнал, который добавляется к общей сумме. Оставшиеся 25% объема второго элемента объема заполнены вторым элементом заряда, так что плотность заряда остается той же самой – ρ. В следующий момент времени, все тот же первый элемент заряда займет 50% третьего элемента объема – и внесет 50% вклада в сигнал от него; второй элемент заряда тоже внесет 50% вклада. Плотность заряда та же. И т.д.
На следующем рисунке проиллюстрирована эта процедура суммирования для v = 0.75 c.
⦾⦾⦾⦾
⎕⎕⎕⎕⦾⦾⦾⦿
⎕⎕⎕⎕⎕⎕⎕⎕⦾⦾⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦾⦿⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿⦿◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿◍◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿◍◍◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕◍◍◍◍
Здесь ⦾ обозначает 25% первого элемента заряда, ⦿ - 25% второго элемента заряда, ◍ - 25% третьего элемента заряда, ⎕⎕⎕ - элементы объема, которые более не вносят вклад в суммарный потенциал.
Интересно девки пляшут, по четыре сразу в ряд. При такой процедуре суммирования, каждый элемент заряда внесет свой вклад в сигнал не один раз, а 4 раза, потому что он успевает несколько раз «отметиться» в разных элементах объема (вклад всех, кроме первого и последнего элементов заряда, сначала растет от 25% до 100%, потом опять убывает до 25%). В этом и заключается физический смысл уравнения Лиенара-Вихерта. Это уравнение стоит на идее, что суммировать сигнал от заряда надо не по элементам заряда, а по тому объему пространства, через который заряд пройдет за время путешествия сигнала от дальнего конца заряда к ближнему, причем суммирование производится таким образом, что каждый элемент заряда учитывается не один, а много раз.
Я думаю, что намного больше физического смысла имеет иная процедура суммирования (то есть иная процедура взятия интеграла по объему) – по самим элементам заряда. При этой процедуре, каждый элемент заряда вносит вклад в общий потенциал только один раз. Допустим, для v = 0.9 c, суммирование будет выглядеть следующим образом:
В первый момент времени, сигнал излучается самым дальним элементом заряда. Во второй момент времени, сигнал излучается вторым элементом заряда, который за это время успел сместиться на расстояние 9w. В третий момент времени, сигнал излучается третьим элементом заряда, который за это время успел сместиться еще на расстояние 9w. И так далее. В итоге, каждый элемент заряда внесет свой вклад в суммарный потенциал только один раз и уравнение для потенциала будет, все-таки:
g = f / r’
Для иллюстрации:
◘■■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□■◘■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□■■◘■■□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■◘■□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■■◘
Здесь ◘ - элемент заряда, который излучает сигнал в данный момент времени, ■■■ – остальные элементы заряда, сигнал от которых в данный момент не учитывается, □□□ – элементы пустого пространства.
Приведу еще один аргумент. Я ранее писал:
Любая переменная f, для которой можно записать волновое уравнение вида
∂²f/∂t² – c²∇²f = S(x – ξ, y, z, t – ԏ)
имеет фронты волн, распространяющиеся со скоростью c. Производная f по r’ всегда будет приобретать ЛВД множитель 1 / (1– r’∙v / (r’c)), каков бы ни был вид зависимости самой f от r’.
Интересно получается. Производная по расстоянию r’ обязательно должна приводить к появлению ЛВД множителя (вот здесь это уже несомненно – я сам проверил :) ). А Лиенар с Вихертом утверждают, что и интеграл по объему (главный вклад в который вносит именно интеграл по направлению r') – тоже приведет к появлению того же множителя. Как это так? Математические манипуляции, противоположные по смыслу и обычно по своему результату, вдруг приводят к одному и тому же результату?
Иными словами, я утверждаю, что физика пользуется неправильной процедурой интегрирования по объему для процессов, меняющихся со временем (а также рядом других математических процедур, которые мы рассмотрим позже). Те самые "гениальные дикари" XVIII-XIX веков совершили математические ошибки - и эти ошибки стали фундаментом физики.
Это был сравнительно более простой (совсем без математики не получилось) пересказ некоторых идей, высказанных ранее. На самом деле, это всё пока что затянувшееся введение, всё то же набившее, наверно, оскомину «нулевое приближение». Пора мне переходить уже к действительно интересным вещам – к первому приближению, для начала. Здесь я дам действительно качественную трактовку, на пальцах. Может быть, имеет даже смысл коротко, на пальцах дать общую картину моего видения «новой физики», а также того, в чем я вижу основные ошибки математики и примкнувшей к ней физики. Общий обзор, а потом перейдем к деталям. Попробую.
Итак, задача формулируется следующим образом. Мы хотим знать, чему равен потенциал от движущегося заряда в момент времени t в покоящейся точке P. Это делается при помощи интеграла по объему от плотности заряда и расстояния до заряда в момент излучения сигнала:
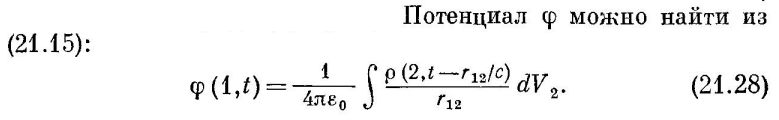
Поскольку заряд движется, то для того, чтобы достичь точки Р одновременно, сигналы от разных частей заряда должны быть излучены в разные моменты времени. Чем дальше от точки Р находится какой-то элемент заряда, тем раньше должен быть излучен сигнал от него. Причем за то время, пока сигнал от самого дальнего элемента заряда дойдет до самого ближнего элемента, этот ближний элемент успеет пройти какое-то расстояние.
Уравнения динамики записываются обычно в 2 формах - лагранжевой и эйлеровой. Уравнения в форме Лагранжа описывают движения индивидуальной частицы жидкости или твердого тела. Уравнения в форме Эйлера описывают то, что происходит в некотором элементе объема пространства. Рассматриваются силы, скорости, смещения и т.д. применительно именно к этому малому элементу пространства; судьба индивидуальных частиц при этом не важна. На примере реки: Лагранж интересуется движением индивидуальных частиц жидкости, а Эйлер – скоростями и пр. в определенной точке пространства, где одни частицы постоянно сменяются другими.
Задача определения потенциала от движущегося заряда является ярким примером подхода Эйлера. Решается она так:
Для простоты, будем считать, что заряд имеет кубическую форму и точка Р находится прямо по направлению движения заряда, на оси движения. Объем пространства, через который пройдет заряд за то время, пока сигнал от самого дальнего от точки Р элемента заряда путешествовал до самого ближнего элемента, разбивается на элементы толщиной w. Суммарный потенциал в точке Р определяется как сумма сигналов от каждого элемента объема, излученных в последовательные моменты времени (разница между которыми dt = w/c). Подчеркиваю – от каждого элемента объема, а не элемента заряда. Допустим, для примера, что скорость источника v = 0.75 c. Процедура суммирования сигналов такова:
Сначала к сумме добавляется сигнал от самого дальнего элемента объема, где в этот момент находится первый элемент заряда с толщиной w и плотностью заряда ρ. Потом мы переходим к следующему элементу объема толщиной w и добавляем к сумме его сигнал, излученный в момент времени dt = w/c. За это время, первый элемент заряда успел частично сместиться во второй элемент объема, так что 75% второго элемента объема будут заполнены первым элементом заряда – и он опять вносит вклад в сигнал, который добавляется к общей сумме. Оставшиеся 25% объема второго элемента объема заполнены вторым элементом заряда, так что плотность заряда остается той же самой – ρ. В следующий момент времени, все тот же первый элемент заряда займет 50% третьего элемента объема – и внесет 50% вклада в сигнал от него; второй элемент заряда тоже внесет 50% вклада. Плотность заряда та же. И т.д.
На следующем рисунке проиллюстрирована эта процедура суммирования для v = 0.75 c.
⦾⦾⦾⦾
⎕⎕⎕⎕⦾⦾⦾⦿
⎕⎕⎕⎕⎕⎕⎕⎕⦾⦾⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦾⦿⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿⦿⦿
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿⦿◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿⦿◍◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⦿◍◍◍
⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕◍◍◍◍
Здесь ⦾ обозначает 25% первого элемента заряда, ⦿ - 25% второго элемента заряда, ◍ - 25% третьего элемента заряда, ⎕⎕⎕ - элементы объема, которые более не вносят вклад в суммарный потенциал.
Интересно девки пляшут, по четыре сразу в ряд. При такой процедуре суммирования, каждый элемент заряда внесет свой вклад в сигнал не один раз, а 4 раза, потому что он успевает несколько раз «отметиться» в разных элементах объема (вклад всех, кроме первого и последнего элементов заряда, сначала растет от 25% до 100%, потом опять убывает до 25%). В этом и заключается физический смысл уравнения Лиенара-Вихерта. Это уравнение стоит на идее, что суммировать сигнал от заряда надо не по элементам заряда, а по тому объему пространства, через который заряд пройдет за время путешествия сигнала от дальнего конца заряда к ближнему, причем суммирование производится таким образом, что каждый элемент заряда учитывается не один, а много раз.
Я думаю, что намного больше физического смысла имеет иная процедура суммирования (то есть иная процедура взятия интеграла по объему) – по самим элементам заряда. При этой процедуре, каждый элемент заряда вносит вклад в общий потенциал только один раз. Допустим, для v = 0.9 c, суммирование будет выглядеть следующим образом:
В первый момент времени, сигнал излучается самым дальним элементом заряда. Во второй момент времени, сигнал излучается вторым элементом заряда, который за это время успел сместиться на расстояние 9w. В третий момент времени, сигнал излучается третьим элементом заряда, который за это время успел сместиться еще на расстояние 9w. И так далее. В итоге, каждый элемент заряда внесет свой вклад в суммарный потенциал только один раз и уравнение для потенциала будет, все-таки:
g = f / r’
Для иллюстрации:
◘■■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□■◘■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□■■◘■■□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■◘■□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■■◘
Здесь ◘ - элемент заряда, который излучает сигнал в данный момент времени, ■■■ – остальные элементы заряда, сигнал от которых в данный момент не учитывается, □□□ – элементы пустого пространства.
Приведу еще один аргумент. Я ранее писал:
Любая переменная f, для которой можно записать волновое уравнение вида
∂²f/∂t² – c²∇²f = S(x – ξ, y, z, t – ԏ)
имеет фронты волн, распространяющиеся со скоростью c. Производная f по r’ всегда будет приобретать ЛВД множитель 1 / (1– r’∙v / (r’c)), каков бы ни был вид зависимости самой f от r’.
Интересно получается. Производная по расстоянию r’ обязательно должна приводить к появлению ЛВД множителя (вот здесь это уже несомненно – я сам проверил :) ). А Лиенар с Вихертом утверждают, что и интеграл по объему (главный вклад в который вносит именно интеграл по направлению r') – тоже приведет к появлению того же множителя. Как это так? Математические манипуляции, противоположные по смыслу и обычно по своему результату, вдруг приводят к одному и тому же результату?
Иными словами, я утверждаю, что физика пользуется неправильной процедурой интегрирования по объему для процессов, меняющихся со временем (а также рядом других математических процедур, которые мы рассмотрим позже). Те самые "гениальные дикари" XVIII-XIX веков совершили математические ошибки - и эти ошибки стали фундаментом физики.
Это был сравнительно более простой (совсем без математики не получилось) пересказ некоторых идей, высказанных ранее. На самом деле, это всё пока что затянувшееся введение, всё то же набившее, наверно, оскомину «нулевое приближение». Пора мне переходить уже к действительно интересным вещам – к первому приближению, для начала. Здесь я дам действительно качественную трактовку, на пальцах. Может быть, имеет даже смысл коротко, на пальцах дать общую картину моего видения «новой физики», а также того, в чем я вижу основные ошибки математики и примкнувшей к ней физики. Общий обзор, а потом перейдем к деталям. Попробую.
Отредактировано: Yuri Rus - 02 дек 2019 в 12:41
- +0.00 / 0
-
Карма: -98.57
Регистрация: 11.08.2007
Сообщений: 1,173
Читатели: 0
Аккаунт заблокирован
Регистрация: 11.08.2007
Сообщений: 1,173
Читатели: 0
Аккаунт заблокирован
Цитата: Yuri Rus от 30.05.2011 05:30:03
Иными словами, я утверждаю, что физика пользуется неправильной процедурой интегрирования по объему для процессов, меняющихся со временем (а также рядом других математических процедур, которые мы рассмотрим позже).
Неправильность в чем состоит можете сформулировать чуть четче?
Мат физика нынешняя занимается тем, что подгоняет матмодель под ряд экспериментальных данных в лучшем случае.И что им можно предьявить?Модель показала хорошую сходимость,берите, используйте..вот и вся аргументация.

P.S.Мы тут.

Отредактировано: SvK - 01 июн 2011 в 09:57
В мире нет ничего Абсолютного..
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: SvK от 01.06.2011 09:55:34
Неправильность в чем состоит можете сформулировать чуть четче?
Мат физика нынешняя занимается тем, что подгоняет матмодель под ряд экспериментальных данных в лучшем случае.И что им можно предьявить?Модель показала хорошую сходимость,берите, используйте..вот и вся аргументация.
P.S.Мы тут.
Для частного случая - интегрирования по объему двигающегося заряда (то есть здесь спрятано интегрирование и по времени, которое более явно видно в процедуре интегрирования при помощи дельта-функции) - я объяснил, что ошибка заключается в том, что каждый элемент заряда вносит вклад в интеграл несколько раз.
Для общего случая (а что тогда является правильной процедурой интегрирования по объему вообще, для любых процессов) - надо подумать. Я собираюсь об этом и близких вопросах вскоре говорить. Это комплекс вопросов и ошибочных (по моему мнению) процедур мат. физики; говорить об одной только ошибке или процедуре мне затруднительно, я вижу это как спутанный клубок. Тут и решение неоднородного волнового уравнения, и принцип суперпозиции, и разделение векторного поля на соленоидное (вихревое) и безвихревое, и ряд других вопросов.
Мой план сейчас такой: сначала я поговорю об эксперименте Майкельсона и его объяснении за счет искривления лучей. Аналогично - поперечный эффект Доплера для света (почему частота уменьшается в гамма раз). Затем дам качественное изложение "первого" и "второго приближений" - взаимодействие последовательных волн, движение сферы в жидкости и пр. Потом уже буду говорить о том, почему это все требует использования другой мат. физики, изменения ряда стандартных мат. операций. Но вначале я буду стараться говорить качественно, на пальцах.
Собственно, хотя я говорю об изменении математики, использовании более сложных диф. уравнений с бОльшим числом переменных, эта математика в тысячу раз проще, чем та математика, которая применяется физиками-теоретиками сейчас. Произойдет небольшое усложнение вначале - для простых задач, типа неоднородного волнового уравнения, - а потом огромное упрощение всех остальных задач, которые сейчас записываются крайне сложным образом.
Мое решение, на самом деле, фантастически, смехотворно простое. Настолько простое, что "так не бывает". И вопрос - почему этого никто не заметил раньше, ведь это безумно просто (или просто безумно, кому как нравится), - будет задан тысячу раз. Почему - не знаю. Но то, что я предлагаю, действительно крайне просто. На уровне 6-7 класса.
Те самые "медведи", о которых я писал в первом сообщении данной ветки.
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Я пишу сейчас статью с разбором эксперимента Майкельсона-Морли и у меня возникла проблема. Лет 8-10 назад, я нашел где-то в интернете фотографии интерференционных полосок, полученных Майкельсоном, Майкельсоном и Морли, Морли и Миллером, и Миллером. Я сохранил их на компьютере, но я сменил несколько компьютеров с того времени и сейчас найти эти фотографии не могу. Жаль; это было бы очень наглядной иллюстрацией того, что я имею сказать по поводу данного метода. Если кому-то попадались такие фотографии, буду благодарен за ссылку, где их можно скачать. Или, если не затруднит, выложите их на каком-то сайте типа Photobucket.
Пока же рекомендую замечательный сайт "Эфирный Ветер" (http://ivanik3.narod.ru/index.html), созданный несколько лет назад новосибирским ученым (я знаю только его имя - Иван). Там собрана прекрасная коллекция классических статей и книг по вопросам, связанным с эфиром, теорией относительности и электродинамикой. Иван сам сканировал их в библиотеке Академгородка, проделал огромную работу. Сайт, к сожалению, работает довольно медленно (он на Народ.ру). Было бы неплохо создать зеркало сайта со всеми статьями и книгами на более быстром сервере, если Иван согласится.
Вот страница этого сайта со статьями. посвященными экспериментам по определению движения Земли относительно эфира с точностью второго порядка (Майкельсон-Морли и подобные):
http://ivanik3.narod.ru/linksMM-VAA.html
В интернете множество "мертвых ссылок" на сайты, которые перестали поддерживаться их создателями. Было бы жаль, если вся эта работа, проделанная Иваном, пропала, если он не сможет заниматься более своим сайтом, по тем или иным причинам. Я сам, к сожалению, не знаю, как скопировать сайт целиком, могу делать это только для отдельных страниц или статей. Никто не подскажет, как это сделать?
Пока же рекомендую замечательный сайт "Эфирный Ветер" (http://ivanik3.narod.ru/index.html), созданный несколько лет назад новосибирским ученым (я знаю только его имя - Иван). Там собрана прекрасная коллекция классических статей и книг по вопросам, связанным с эфиром, теорией относительности и электродинамикой. Иван сам сканировал их в библиотеке Академгородка, проделал огромную работу. Сайт, к сожалению, работает довольно медленно (он на Народ.ру). Было бы неплохо создать зеркало сайта со всеми статьями и книгами на более быстром сервере, если Иван согласится.
Вот страница этого сайта со статьями. посвященными экспериментам по определению движения Земли относительно эфира с точностью второго порядка (Майкельсон-Морли и подобные):
http://ivanik3.narod.ru/linksMM-VAA.html
В интернете множество "мертвых ссылок" на сайты, которые перестали поддерживаться их создателями. Было бы жаль, если вся эта работа, проделанная Иваном, пропала, если он не сможет заниматься более своим сайтом, по тем или иным причинам. Я сам, к сожалению, не знаю, как скопировать сайт целиком, могу делать это только для отдельных страниц или статей. Никто не подскажет, как это сделать?
- +0.00 / 0
-
Карма: +23.58
Регистрация: 21.01.2009
Сообщений: 808
Читатели: 0
Регистрация: 21.01.2009
Сообщений: 808
Читатели: 0
Цитата: Yuri Rus от 26.05.2011 21:28:11
При движении заряженной частицы, ее электрическое поле в направлении движения сокращается в γ раз, где
γ = 1 / (1 - v²/c²)½
Давайте как отправную точку возьмем этот аргумент и обсудим его. Он достаточно простой. Есть вопросы, возражения?
Это не так. (В традиционной физике).
Если аккуратно все проделать (или посмотреть вывод Био-Савара-Лапласа с помощью преобразования Лоренца), то:
поле в направлении движения сокращается, но не в γ раз, а просто домножается на (1 - v²/c²). А в направлении, перпендикулярном к движению, поле _возрастает_ (делится на (1 - v²/c²)½ ). Дело в том, что при переходе к другой с.к. преобразуется по Лоренцу как само поле (4-тензор ранга 2), так и расстояние, на котором оно действует.
Теперь задачка для детей. Есть прямолинейный проводник с током. Будет ли к нему притягиваться или отталкиваться точечный покоящийся заряд из-за того что электроны движутся, а ионы покоятся?
Ответ нет (как легко было догадаться). Я честно все проделал, но для Солнца поленился. Тем более, что там и скорости в среднем не постоянные по объему.
**********************
Короче говоря, Юрий_Рус: что Вы предлагаете? Отказаться от принципа относительности? Тогда будет выделенная система отсчета. Можно разработать и такую физику, кто спорит. Но, скорее всего, Вы получите все те же результаты, но гораздо более сложным и через*опистым образом. Был же опыт у Птолемея с Коперником. У Птолемея все верно, ошибок нет. Но у Коперника проще. У Вас, скорее всего, будет так же. Только хронологически наоборот. В роли Коперника Минковский, а Вы в роли Птолемея.
- +0.00 / 0
-

Москва
21 год
Карма: +385.51
Регистрация: 22.07.2010
Сообщений: 6,015
Читатели: 7
Регистрация: 22.07.2010
Сообщений: 6,015
Читатели: 7
Цитата: Pnb от 04.06.2011 16:39:08
Теперь задачка для детей. Есть прямолинейный проводник с током. Будет ли к нему притягиваться или отталкиваться точечный покоящийся заряд из-за того что электроны движутся, а ионы покоятся?
Задачка некоректная, т.к. скорость упорядочного движения электронов в проводнике под воздействием электрического поля 10-4 - 10-3 м/с, а скорость теплового движения электронов 105 м/с, т.е. эфект с током - без тока на нуле.
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: Pnb от 04.06.2011 16:39:08
Это не так. (В традиционной физике).
Если аккуратно все проделать (или посмотреть вывод Био-Савара-Лапласа с помощью преобразования Лоренца), то:
поле в направлении движения сокращается, но не в γ раз, а просто домножается на (1 - v²/c²). А в направлении, перпендикулярном к движению, поле _возрастает_ (делится на (1 - v²/c²)½ ). Дело в том, что при переходе к другой с.к. преобразуется по Лоренцу как само поле (4-тензор ранга 2), так и расстояние, на котором оно действует.
Да, это моя ошибка, признаю. Я в тот момент, когда это писал, забыл, что электрическое поле движущегося заряда в перпендикулярном направлении возрастает. Странно, что остальные читатели на это сразу же не обратили внимания. Тем не менее, давайте посмотрим, будет ли иметь место полная компенсация уменьшения поля в направлении движения за счет возрастания поля в направлении, перпендикулярном движению. Ведь коэффициенты усиления-ослабления в этих направлениях разные - при малых скоростях, β << 1, для перпендикулярного поля мы имеем усиление на β²/2:
γ - 1 = 1/(1 - β²)½ - 1 ≈ β²/2
а по направлению движения - ослабление на β²
(1 - β²) - 1 = - β²
Разница, получается, все равно на β²/2 = γ - 1. Или я опять что-то напутал?
Как я уже написал, я от этого именно аргумента давным-давно ушел и забыл про него (всех деталей тех старых своих рассуждений уже не помню; я помнил, что поля по направлению движения и перпендикулярно ему, различаются в γ раз, но, вишь, забыл, что поле по направлению движения падает в γ² раз, а перпендикулярно ему - растет в γ раз; что значит давно не заниматься физикой). Сейчас этот аргумент никак не влияет на мое отношение к теории относительности и к классической физике.
Цитата: Pnb от 04.06.2011 16:39:08
Теперь задачка для детей. Есть прямолинейный проводник с током. Будет ли к нему притягиваться или отталкиваться точечный покоящийся заряд из-за того что электроны движутся, а ионы покоятся?
Ответ нет (как легко было догадаться). Я честно все проделал, но для Солнца поленился. Тем более, что там и скорости в среднем не постоянные по объему.
Здесь дело не в том, что внутри Солнца электроны движутся, а ионы покоятся. А в том, что электроны движутся во всех направлениях (так же, как тепловые электроны в проводнике без тока), а потому их магнитные поля компенсируют друг друга. Сами по себе - невзирая на то, что делают ионы.
Цитата: Pnb от 04.06.2011 16:39:08
Короче говоря, Юрий_Рус: что Вы предлагаете? Отказаться от принципа относительности? Тогда будет выделенная система отсчета. Можно разработать и такую физику, кто спорит. Но, скорее всего, Вы получите все те же результаты, но гораздо более сложным и через*опистым образом. Был же опыт у Птолемея с Коперником. У Птолемея все верно, ошибок нет. Но у Коперника проще. У Вас, скорее всего, будет так же. Только хронологически наоборот. В роли Коперника Минковский, а Вы в роли Птолемея.
Да, я предлагаю отказаться от принципа относительности Эйнштейна и использовать только принцип относительности Галилея. Да, будет выделенная система отсчета - она реально регистрируется, кстати. Связанная с микроволновым излучением.
Все наоборот - это Минковский в роли Птолемея, а я - Коперника. Кстати, если Вы откроете "Альмагест" Птолемея (где-то в самом начале, глава не то 6, не то 9), то увидите, что о возможности гелиоцентрической модели и вращения Земли вокруг своей оси он прекрасно знал. Но отвергал ее на основании чего? Правильно, отсутствия наблюдаемого ветра на поверхности Земли. Птолемей не знал о том, что атмосфера Земли вращается вместе с самой Землей, и предполагал, что если бы Земля вращалась вокруг своей оси (а также вокруг Солнца), то мы наблюдали бы сильнейший ветер. Диаметр Земли к тому времени был хорошо известен и рассчитать скорость этого ветра не представляло сложности.
Вам это ничего не напоминает? Отсутствия наблюдаемого эфирного ветра, например, при движении Земли по орбите?
Отредактировано: Yuri Rus - 04 июн 2011 в 19:36
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: ДядяВася
Посмотрите типа этого http://chocasativa.a….php?f=140 , http://chip.com.ua/413011.html или какие либо менеджеры закачки их в инете много в т.ч. бесплатные.
Спасибо, попробую это сделать. На сайте Ивана очень много ценнейших статей, которые самому разыскивать - очень большая работа (и еще нужно знать о их существовании). Будет жаль, если вся эта работа пропадет, когда Иван перестанет поддерживать свой сайт.
Я, кстати, всем рекомендую скачать себе весь сайт Ивана. Кого интересует физика, конечно.
- +0.00 / 0
-
Карма: +23.58
Регистрация: 21.01.2009
Сообщений: 808
Читатели: 0
Регистрация: 21.01.2009
Сообщений: 808
Читатели: 0
Цитата: Yuri Rus от 04.06.2011 19:07:03
будет ли иметь место полная компенсация уменьшения поля в направлении движения за счет возрастания поля в направлении, перпендикулярном движению. Ведь коэффициенты усиления-ослабления в этих направлениях разные - при малых скоростях, β << 1, для перпендикулярного поля мы имеем усиление на β²/2:
γ - 1 = 1/(1 - β²)½ - 1 ≈ β²/2
а по направлению движения - ослабление на β²
(1 - β²) - 1 = - β²
Разница, получается, все равно на β²/2 = γ - 1. Или я опять что-то напутал?
Если через какую-то точку пролетают одновременно большое число зарядов. Все имеют скорости одинаковые по абсолютной величине, но направления скоростей различны и равномерно распределены по сфере. Будет ли электрическое поле, создаваемое этими зарядами таким же, как и случае, когда они все покоятся в этой точке?
Ответ: да.
Т.е. компенсация будет иметь место. Это я зря испугался/поленился. Интеграл по сфере будет точно тот же, что и для линейного проводника (даже берущийся).
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: Pnb от 04.06.2011 20:59:35
Если через какую-то точку пролетают одновременно большое число зарядов. Все имеют скорости одинаковые по абсолютной величине, но направления скоростей различны и равномерно распределены по сфере. Будет ли электрическое поле, создаваемое этими зарядами таким же, как и случае, когда они все покоятся в этой точке?
Ответ: да.
Т.е. компенсация будет иметь место. Это я зря испугался/поленился. Интеграл по сфере будет точно тот же, что и для линейного проводника (даже берущийся).
А вот здесь, пожалуйста, поподробнее. Это откуда следует? Раз уж Вы говорите про интеграл по сфере, так напишите, как он выглядит. А то я не очень понимаю, про какой именно интеграл Вы говорите. И непонятна Ваша логика.
Вот посмотрите: Если мы проведем экви-поверхности электрической напряженности Е (они не совпадают с эквипотенциальными поверхностями φ, потому что вклад в Е вносит еще и А, и форма у эллипсоидов Е будет, как мы выяснили благодаря Вашему напоминанию, более плоской, чем у эллипсоидов φ), то, если так можно выразитья, «объем» этих эллипсоидов Е для движущихся электронов будет меньше в ту же самую γ раз, чем «объем» сферы Е для покоящихся электронов. Математически говорить про «объем» эллипсоидов Е, возможно, неправильно, но смысл, надеюсь, понятен. Ведь тот интеграл, про который Вы говорили, он же должен быть по объему, и вот это отличие «объема» эллипсоидов (они сжаты в γ² раз по оси движения и растянуты в γ раз в перпендикулярной плоскости: γ / γ² = 1 / γ) от объема сферы и должно привести к тому, что суммарное электрическое поле всех движущихся электронов будет ослаблено, по сравнению с полем покоящихся электронов. Я понимаю, что я сейчас выражаюсь неправильно с точки зрения математических терминов, просто, рассуждая «на пальцах», мне проще говорить про «объем» эллипсоида напряженности, чем искать более правильный математический термин.
Итак, все электроны проходят одновременно через одну точку во всех возможных направлениях и с одинаковой скоростью. Мы измеряем поле Е на расстоянии R от этой точки и сравниваем его с полем покоящихся электронов. Поскольку β << 1, мы можем использовать линейную аппроксимацию для отличий полей Е разных электронов от сферического. Тогда в поперечном направлении увеличенное в γ раз поле будет отличаться от сферического на γ – 1 ≈ β²/2, а уменьшенное в γ² раз в направлении движения поле будет отличаться от сферического на (1 - β²) - 1 = - β². И все промежуточные значения для других углов.
Так вот, я очень удивлюсь, если сумма (интеграл) таких сплющенных полей электронов, двигающихся под всеми возможными углами, не будет отражать вот это самое отличие в «объемах» эллипсоида и сферы. Потому что, если Вы представите этот экви-эллипсоид наложенным на сферу, а затем начнете его мысленно поворачивать относительно сферы (эти повернутые эллипсоиды соответствуют разным направлениям движения электронов), то «торчать» над поверхностью сферы будет меньшая часть экви-эллипсоидов, чем недоставать до ее поверхности. Кроме того, «недостающие» экви-эллипсоиды будут недоставать на бОльшую величину, чем «торчащие» - торчать. Я понятно выразился? Та величина, на которую повернутый экви-эллипсоид недостает до поверхности сферы, пропорциональна (в линейной аппроксимации) уменьшению значения Е в этой точке. Аналогично с "торчащими" экви-эллипсоидами - та величина, на которую повернутый экви-эллипсоид торчит выше поверхности сферы, пропорциональна увеличению значения Е в этой точке. Суммируя, мы и должны получить ослабление поля всех электронов, движущихся через одну точку во всех направлениях, примерно в γ раз. Именно как следствие уменьшения «объема» экви-эллипсоида в γ раз.
Далее, в прошлом моем ответе я написал про магнитное поле (там, где Вы говорили о проводнике с током). А сейчас усомнился - а Вы его имели в виду? Пишите более четко, плиз, а то мы, возможно, говорим о разном. дядяВася, кстати, отвечая Вам, писал о скорости миграции электронов в проводнике с током, в противоположность тепловой скорости электронов в том же проводнике. Я и его понял так, что он говорит о магнитном поле. Если же и Вы, и дядяВася говорили все-таки об электрическом поле электронов в проводнике, то это совсем другое дело.
Хорошо, рассмотрим электрическое поле, создаваемое электронами, "мигрирующими" во внешнем электрическом поле со скоростью, скажем, 1 мм/с, то есть 10-3 м/с. Это поле, опять же, в поперечном направлении, будет сильнее в γ раз, чем поле покоящихся ионов. А по оси движения – слабее в γ² раз. Но эта задача совершенно не идентична рассмотренной выше задаче, где электроны одновременно проходили через одну точку во всех возможных направлениях. Потому что электроны проводника более не двигаются во всех направлениях (мы не учитываем тепловое движение), они мигрируют в одном направлении. Все электрические поля сжаты одинаково, по одной и той же оси (вдоль проводника). И «поперечные" поля вносят больший вклад, чем «продольные» поля: они действуют по кратчайшей прямой, связывающей пробный заряд с проводником, а «продольные» поля – под разными углами и на разных расстояниях, всегда бОльших, чем эта кратчайшая прямая.
Вообще говоря, я здесь «на пальцах» не могу сходу сказать, будет ли суммарное поле таким же, как в случае покоящихся ионов или нет. Это более сложный случай. Здесь надо думать и писать более сложные уравнения и интегралы. Не исключаю, что полная компенсация здесь возможна. Но пока не знаю.
Отредактировано: Yuri Rus - 05 июн 2011 в 11:58
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: PnbПопробую.
2) Все ли понятно в условии
Если через какую-то точку пролетают одновременно большое число зарядов. Все имеют скорости одинаковые по абсолютной величине, но направления скоростей различны и равномерно распределены по сфере. Будет ли электрическое поле, создаваемое этими зарядами таким же, как и случае, когда они все покоятся в этой точке?
На всякий случай, что значит направления скоростей равномерно распределены по сфере. Пусть сумма всех зарядов Q. Рассмотрим единичную сферу S и участок этой сферы dS. Тогда суммарный заряд тех частиц, у которых вектор скорости протыкает этот участок, равен dQ = dS * Q / 4π и зависит только от площади участка, но не от его формы или расположения на сфере.
3) Формула, которая не выписывалась, но использование которой подразумевалось.
E = (q / R²) * (1 - v²/c²) / (1 - v²/c²sin²θ)3/2
Здесь θ - угол между направлением движения и радиус-вектором от заряда к точке наблюдения.
Отсюда при θ = 0 и при θ = π/2
E_min = (q / R²) * (1 - v²/c²), E_max = (q / R²) / (1 - v²/c²)1/2 - эти выписывались.
4)Это не эллипсоиды. Может быть, еще и в этом дело: кривая в полярных координатах с уравнением
ρ(θ) = 1 / (1 - v²/c²sin²θ)3/2 - вовсе не эллипс.
5) Пусть теперь у нас есть заряды, пролетающие через какую-то точку P, и точка наблюдения O. Они создают в точке O электрическое поле, равное интегралу по единичной сфере (с центром P, как удобно представлять себе) от
(dQ / R²) * (1 - v²/c²) / (1 - v²/c²sin²θ)3/2,
где: R - расстояние PO, θ - угол между вектором PO и радиус-вектором текущей точки сферы (от P к текущей точке), который соответствует вектору скорости частицы. v - величина скорости частиц (v = const).
Подставим dQ, получим интеграл по единичной сфере от
(dS * Q / 4πR²) * (1 - v²/c²) / (1 - v²/c²sin²θ)3/2.
Он берется и равен Q / R². Не зависит от v.
АУ, т.к. такие пассажи абсолютно не читаемы.
Подставим dQ, получим интеграл по единичной сфере от
(dS * Q / 4πR²) * (1 - v²/c²) / (1 - v²/c²sin²θ)3/2.
Он берется и равен Q / R². Не зависит от v.
Вы слишком торопитесь и следить за Вашей аргументацией очень трудно. Вы просто делаете некое утверждение, а на чем оно основано - догадывайся как хочешь. Предположим, что до этого момента у Вас все было правильно. Но вот решение этого интеграла надо написать подробно. Откуда следует, что он не зависит от v и γ? Я, например, вижу v в подынтегральном выражении. Приведите, пожалуйста, или источник (книгу, где такой интеграл взят) или распишите подробно его решение. Я лично не знаю, чему он равен. Решение определенных интегралов - это отнюдь не тривиальная задачка. Обратите внимание, насколько детально я расписываю вывод всех формул - чтобы любой читатель мог проследить за всеми шагами и не обязан был гадать, откуда что взялось, или верить мне на слово.
Так что не могли бы Вы все-таки детально расписать, откуда у Вас берется независимость Вашего интеграла от скорости? И желательно со ссылками на учебники.
P.S. Скажем, вот вывод уравнения для Е из 2-го тома Ланда-Лившица, стр. 129-130:


Интеграл же (или сумму) по полям Е движущихся электронов я пока нигде не нашел. Отсюда вопрос - Вы решение этого интеграла видели в какой-то книге или сами его решили?
Отредактировано: Yuri Rus - 02 дек 2019 в 12:43
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: PnbСам решил, естественно. Я же говорю, берущийся.
∫∫S(dS * Q / 4πR²) * (1 - v²/c²) / (1 - v²/c²sin²θ)3/2 =
∫dφ∫(Q / 4πR²) (1 - v²/c²) (1 - v²/c²sin²θ)-3/2sinθ dθ;
здесь (φ, θ) - сферические координаты, sinθ - якобиан (dS = sinθ dφdθ). При этом θ - то же что и раньше, φ - полярный угол в плоскости, перпендикулярной к отрезку PO; 0 < φ < 2π, 0 < θ < π.
Выносим все константы и ∫dφ = 2π; обозначаем β² := v²/c², получаем
(Q / 4πR²)2π(1 - β²) ∫(1 - β²sin²θ)-3/2sinθ dθ =
Q (1 - β²) / (2R²) ∫- (1 - β²(1 - cos²θ))-3/2 dcosθ = (замена c := cosθ, -1 < c < 1, + из-за перестановки пределов интеграла) =
Q (1 - β²) / (2R²) ∫+ ((1 - β²) + β²c²)-3/2 dc = (выносим β² и обозначаем λ² := (1 - β²)/β² ) =
Q (1 - β²) β-3/(2R²) ∫(λ² + c²)-3/2 dc =
(замена c = λ tgξ, ξ := arctg(c/λ), -arctg(1/λ) < ξ < arctg(1/λ), λ² + c² = λ²/cos²ξ, dc = λdξ / cos²ξ ) =
Q (1 - β²) β-3/(2R²) ∫λ-3 cos3ξ λ dξ / cos²ξ =
Q (1 - β²) β-3λ-2/(2R²) ∫cosξ dξ =
Q (1 - β²) β-3λ-2/(2R²) sin ξ │(подстановка -arctg(1/λ) < ξ < arctg(1/λ) , при этом
sin (arctg(1/λ)) = 1 / (λ² + 1)1/2 ) =
Q (1 - β²) β-3λ-2 2 / (2R² (λ² + 1)1/2) = (возвращаемся к β, λ² + 1 = 1/β² ) =
Q (1 - β²) β-3 (β² / (1 - β²) ) β / R² =
Q / R² .
********************************
Юрий Рус!!!!
Я понимаю, все со школы забыли, как интегрировать и что такое якобиан, надо все вспоминать. Но зачем мучить этим читателей. Давайте АУ ставить все же на такое.
Pnb - насчет АУ, в этой ветке все-таки довольно много формул и здесь в данный момент, надо полагать, в основном находяься те, кого формулы не пугают. Я согласен, что слишком много это плохо и в какой-то момент надо чистить ветку от лишнего. Но пока дискуссия развивается, ставить на АУ сутки - это мало. А больший срок (3 дня, неделя) форум не позволяет.
Сейчас, кстати, как раз настал такой момент, когда последние страницы можно и почистить. Именно чтобы пожалеть других читателей, которые заглянут на ветку в будущем.
Я признаю, что был неправ относительно того, что суммарные поля "быстрых" электронов в звездах будут слабее суммарных полей "медленных" ионов. Они все-таки компенсируются. Вы меня убедили - у меня была ошибка, которая заключалась в том, что я забыл об усилении электрического поля в поперечном направлении.
В Вашем решении интеграла слишком много замен переменных. Я поступил проще: открыл справочник Градштейн И.С., Рыжик И.М. «Таблицы интегралов, сумм, рядов и произведений», 1963. Там есть такой интеграл (берущийся, да):


Тогда
∫ sinθ dθ / (1 – β²sin²θ)3/2 = – cosθ / ((1 – β²)(1 – β²sin²θ)½)
Должен быть еще множитель (1 – β²):
(1 – β²) ∫ sinθ dθ / (1 – β²sin²θ)3/2 = – cosθ / (1 – β²sin²θ)½
β пока не исчезла, но подставим пределы интегрирования от 0 до π:
cos π = -1, cos 0 = 1, sin² π = 0, sin² 0 = 0.
Так что – cosθ / (1 – β²sin²θ)½ в пределах от 0 до π равен просто 2. Зависимость от скорости исчезла.
Это можно было понять и на пальцах - когда я говорил о том, что объем эллипсоида уменьшается, потому что в продольном направлении сжатие происходит в γ² раз, а в поперечном - расширение в γ раз, я ведь был не прав. Потому что в поперечном направлении расширение происходит и по y, и по z, то есть площадь сечения увеличивается все-таки в γ² раз, так что объем эллипсоида остается таким же, как и у сферы. Вот и все доказательство.
Здесь дело в том, что о том, что поля электронов и протонов не должны компенсировать друг друга, я думал, во-первых, больше 25 лет назад (и большинство деталей забыл). Во-вторых, думал в связи с электронами и протонами отдельных атомов, а не в центре звезды. В атоме, если предположить, что электрон двигается с высокой скоростью по определенной орбите, эллипсоид стоит на месте относительно сферы протона. Есть четкие различия в поле вокруг атома, компенсации нет, пусть даже "объемы" эллипсоида и сферы одинаковые. Тогда для меня главным было именно это - формы полей различаются, несмотря на то, что их "объемы" равны.
Квантовая механика решает этот вопрос тем, что отказывается от орбит и движения электронов вокруг ядра. Есть волны вероятности, а движения, получается, нет. Потому что в случае сферического электронного облака для движущихся электронов еще можно применить тот интеграл, о котором мы сейчас говорили, и компенсация полей будет. Но если электронов несколько и их облака не сферические (восьмерки, скажем), то такие электроны двигаются в узком диапазоне пространства и им будут соответствовать определенные фигуры (не эллипсоиды, а более сложные) электрического поля, которые не будут совпадать со сферами протонов. Так что квантовая механика либо отказывается от применения ТО к атомам, либо отказывается от движения электронов внутри атомов (стоячие волны вероятности).
Сейчас же я вспомнил про эти свои рассуждения, но не хотел говорить про движение электронов в атомах, потому что тогда это не вопрос ТО, а вопрос квантовой механики и здесь можно плутать бесконечно. И я решил переформулировать проблему - применить ее не к атомам, а к звездам. Оказалось, зря. Тем более я в этот момент забыл, не знаю как, что поле в поперечном направлении усиливается.
Так или иначе, это был лишь отправной пункт моих рассуждений, много лет назад. Это далеко не главное.
Сейчас же я просмотрю последние 3 страницы и подумаю, что почистить. Написано слишком много. Оставлю только некоторые эпизоды дискуссии на эту тему, а большинство уберу. Пока пусть повисит еще пару дней, все равно у меня нет времени этим заниматься.
Надеюсь, другие участники дискуссии не обидятся, если я делетирую их сообщения.
Отредактировано: Yuri Rus - 02 дек 2019 в 12:57
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: Dobryаk
Этой декларации было бы достаточно... так как после этого ошибочность любого учебника физики сомнений не вызывает.
Если Вы не забыли, то в самом начале ветки я предвидел, что апофеозом будет опровержение потенциалов Лиенара-Вихерта. Уж не знаю, в чем "непреодолимая притягательность Лиенара-Вихерта" (плагиат из Луиса Бюнуэля), но это доказано экспериментально. Во времена СССР во все научные учреждения неудержимым потоком шли т.н. "Письма Трудящихся". Обычно они поступали вначале в Отдел Науки ЦК КПСС, реже в Министерство Обороны, и совсем редко в Академию наук (самое недостойное в научных вопросах учреждение). Рецензию на "Письма трудящихся" зачастую в тысячи (!) страниц надо было писать на самом серьезном уровне, один пример, когда в середине 1970-х была издана книга в полтыщи страниц на мелованной бумаге (редкий художественный альбом издавали на такой высoкокачественной!), описан мной на первой странице "Тикает". А автора той книги, вышедшей уже не знаю каким изданием (а может это кардинально новая теория, отменяющая предыдущую)
http://rutracker.org…?t=2251298
главным достижением которой был неортодоксальный подход к функциям Бесселя в описании движения зарядом по круговым орбитам, где он положил на все лопатки лауреатов Сталинской премии за теорию синхротронного излучения в лице академиков Л.А.Арцимовича и И.Я.Померанчука и профессора Д.И.Иваненко. За последние 35-40 лет клуб почитателей Ильи Герловина
http://isbaza8.ru/ru…orjat.html
http://isbaza8.ru/pr…teina.html
приобрел Вселенские масштабы. Я не знаю, может и Герловин дорос до Лиенара-Вихерта, но раз в десяток лет авторы "Писем трудящихся", за которые отдувался в институте лично я, опровергали именно эти потенциалы (смотрим Бюнуэля).
Муки с "Письмами" удачно закончились в конце 80-х, когда каждый второй депутат горбачевских съездов считал долгом опубликовать свою собственную теорию относительности, гравитации, космологии... так так уже никакого научного рецензирования не осталось. Тогда в Доме научно-технической книги на Ленинском проспекте в Москве на метре книжной полки в отделе "Физика" можно было редко увидеть одну-две действительно научные книжки.
Сегодня свобода печати и любой автор также может опубликовать все что душа пожелает, но научные книги, издаваемые научными издательствами, все же преобладают.
Добряк, слышали такое выражение: "Уходя - уходи"?
Мне с Вами неинтересно разговаривать. Потому что Вы пока еще ни разу не сказали что-нибудь конструктивное, по теме дискуссии, только брюзжите да ехидничаете. И Ваш высокомерный тон, надо сказать, не имеет под собой ну никакого основания. И он начинает надоедать.
Вот я сделал довольно элементарную, надо сказать, ошибку насчет того, что электрическое поле сжимается в гамма раз по оси движения, тогда как на самом деле, согласно ТО, оно сжимается в гамма в квадрате раз, но зато увеличивается в поперечном направлении в гамма раз. Я эту ошибку сделал, потому что последний раз читал ТО примерно 10 лет назад, а с тех пор (периодически, раз в несколько лет) читал только книги по волнам, гидродинамике и т.п. ТО мне стала полностью неинтересна и я многое забыл. Сейчас начал писать про свою теорию, которая рассматривает "классическую" динамику и механику, а ТО касается только постольку-поскольку, как частный вопрос, и ТО не перечитывал. Зря, конечно, я начал говорить об электрическом поле в рамках ТО, надо было все же открыть учебник.
Но вот Вы несколько раз выступили с критическими замечаниями по поводу этого моего аргумента об электрическом поле в рамках ТО (значит, прочитали, что я написал) - и НЕ ЗАМЕТИЛИ моей элементарной ошибки. Зачем-то завели разговор про разложение Фурье для потенциалов, что к теме данного разговора вообще никакого отношения не имело. А элементарной ошибки, которая просто должна бросаться в глаза любому квалифицированному физику, не заметили. Что ставит вопрос о Вашей квалификации. Другие участники форума, кто прокомментировали, в большинстве своем сейчас физикой не занимаются, им можно. А Вы утверждаете, что читаете студентам лекции как раз в этой области.
Я очень спокойно и даже признательно отношусь к любой конструктивной критике. Потому что я, во-первых, сделал в жизни очень многое и мне не стыдно признать, что в чем-то я могу совершить ошибки; это не отразится на моей самооценке. Не ошибается тот, кто ничего не делает - а кто не рискует, тот шампанского не пьет. Во-вторых, потому что вовремя обнаружить, что ты двигаешься в ложном направлении, означает, что ты не потратишь, возможно, слишком много времени на этот ложный путь, прежде чем сам заметишь свою ошибку. Поэтому я всегда признаю свои ошибки - и благодарю за конструктивную критику.
А вот от вас я пока, повторяю, ни разу ничего конструктивного не слышал. И стал сомневаться, что Вы на это способны. Конструктивная критика, на всякий случай объясняю, это: "вот здесь такая-то ошибка", "а как Вы решите такую-то проблему?" и т.п. А вовсе не такое: "это полная ерунда, здесь нечего даже обсуждать", "Фурье, или Лиенар-Вихерт в таком-то году сказали то-то".
И я сомневаюсь, что Вы понимаете, что Вам говорят, я вижу у Вас только рефлекторные реакции, но не осмысление. Вы сослались на вывод Ландау-Лившицем потенциалов Лиенара-Вихерта. Я Вам несколько раз объяснил, что их вывод основан на 4-векторах, следовательно, на геометрии Минковского, а мы говорим об Эвклидовом пространстве. И за основу берем доказательство Фейнмана. Никакой реакции. Повторяете все то же - одни рефлексы, ни проблеска понимания собеседника. Мои аргументы, почему уравнение Лиенара-Вихерта неверно, Вы конструктивно обсуждать (то есть понять предмет беседы и выдать свои мысли) не можете - можете только выдать ссылку на доказательство Ландау-Лившица (которое относится к другому, неэвклидовому, миру).
Вот Вы, оказывается, "отдувались" (словечко, очень хорошо выражающие Ваше отношение к любым нестандартным идеям, которые поступали не по "официальным" каналам, то есть не от других физиков) в Вашем институте за "письма трудящихся", как Вы их назвали. Вам никогда не приходилось читать биографии великих ученых, математиков 18-19 веков? Если бы читали, то, наверно, обратили бы внимание, сколь многие из них начинали свою научную карьеру с того, что именно посылали письма со своими работами признанным в то время ученым. И те тратили свое время на то, чтобы прочесть и потом помогали опубликовать эти работы, рекомендовали молодых дилетантов на открывающиеся вакансии. Сейчас такое отношение полностью невозможно - особенно в физике. Я сужу не по своему опыту - сам я никогда таких писем не посылал, потому что заранее знал, что это бессмысленно. Я читал во многих книгах и статьях профессоров-физиков полу-жалобы, полу-хвастовство о том. как им надоели эти дилетанты, что бомбардируют их своими теориями, которые, конечно, никто из профессоров не читает.
В общем, хотите участвовать в дискуссии конструктивно - welcome. Не хотите - мы с Вами уже один раз прощались. А брюзжание - просто скучно.
Отредактировано: Yuri Rus - 07 июн 2011 в 05:56
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: Dobryаk
Конструктивное, говорите?
Потенциалы Лиенара-Вихерта выведены для движения по прямолинейной траектории из минус в плюс бесконечность. И пользоваться ими для криволинейного движения посто недопустимо. Это "недопустимо" есть самое конструктивное замечание. Вас оно не устраивает.
Это две совершенно разные темы. Сначала я говорил о потенциалах Л-В - для прямолинейного бесконечного движения. Потом, и это совершенно другая тема, о криволинейном движении электронов в звездах - и я ни разу при этом не упомянул про потенциалы Л-В, только отвечая на Ваши слова и все время повторяя, что я говорю здесь об электрическом поле, а не о потенциалах. То есть это Вы все время переводили разговор на эти потенциалы, говоря о криволинейном движении, а не я.
Цитата: Dobryаk
Вас не устраивает принцип суперпозиции?
Но принцип суперпозиции есть элементарное свойство любых ЛИНЕЙНЫХ уравнений в чатных производных, которое очевидно, если решение записано через функцию Грина. Движение заряда, ака линейное преобразование системы координат, не делает линейные уравнения нелинейными.
О принципе суперпозиции я буду говорить позже. Пока я еще не объяснил, что я имел в виду. Да, это свойство линейных уравнений. О том и речь, что уравнения должны быть нелинейными. Я об этом с самого начала говорил.
Цитата: Dobryаk
Вас не устраивает, что мы живем в мире с метрикой Минковского. Кстати, с аких это пор пространство минковского стало искривленным?
Может предьявите нам тензор кривизны? Можете не стараться: это будет математически строгий ноль. Интерсно, а в каком евклидовом пространстве Вы живете и какая в нем метрика?
Да, меня не устраивает пространство Минковского, я считаю и буду стараться обосновать, что наш мир все-таки Эвклидов. О кривизне пространства Минковского я выразился некорректно.
Цитата: Dobryаk
Вас не устраивает современная матфизика в целом... Это лишает физический мир в Вашем воображении какого-либо пересечения с тем, в котором жило и живет остальное человечество. Вас не устраивает вывод в Ландау-Лифшице: у этих авторов функция Грина даже не написана и поля испущенные в разные моменты времени с разных участков трактории они не складывают, а в силу изощренности ума предпочитаютотвт писать сразу.
Да, меня не устраивает матфизика в целом. Я медленно, постепенно пытаюсь обосновать, в чем я вижу ошибки. Пока сказал лишь малую часть. О выводе в Ландау-Лившице я уже сказал много раз, что пространство у них не той системы.
Цитата: Dobryаk
Разложение Фурье, которое как и вся прочая матфизика, Вас не устраивает, не пустой математический трюк. Именно оно в основе всей квантовой теории поля. В посте от 26 Мая 2011, 19:22:26 со всеми ссылками я пояснил, что именно из разложения потенциала Лиенара-Вихерта по Фурье в свое время Ферми сделал губочайшее заключение, что электромагнитное поле ультрарелятивистской частицы похоже на сумму плоских волн --- и все именно в силу сокращения продольных полей. Не хотите знать Ферми, Вайцзекера и Вильямса --- не надо.
Еще о криволинейном движении, точнее, траекториях из прямолинейных участков. Классический пример: траектория с одним изломом в точке рассеяния, которая входит в задачу о т.н. тормозном излучении. По сути решается с другими граничными условиями та же задача Лиенара-Вихерта, хотя эти имена в связи с тормозным излучением редко когда кроме самых-самых старых уже не читаемых книг упоминаются. А вот Ландау и Померанчук в 1953, а за ними Мигдал, пошли дальше, и показали, что многократное рассеяние, т.е., много-много изломов на траектории, кардинально меняет классические формулы Бете-Гайтлера для тормозного излучения. Как оно и положено, теория Ланда-Пмеранчука-Мигдала на опыте подтверждена великолепно, правда на это ушло какие-то 40 лет... Но это должно быть неинтересно, так как их ответ не имеет ничего общего с суммой потенциалов Лиенара-Вихерта, да и получен с корректным применением матфизики и принципа суперпозиции. Так что это замечание тоже надо признать неконструктивным.
И разложение Фурье, и потенциалы Лиенара-Вихерта, и траектория с изломом - все это не имело прямого отношения к теме разговора: электрическому полю движущихся электронов. Это - неадекватные инструменты для решения поставленной задачи. А адекватный инструмент был один - всего лишь формула для сжатия электрического поля, в которой я сам сделал ошибку. Ошибку, которая должна была быть очевидной для любого специалиста. Больше ничего не требовалось. Pnb на эту ошибку указал - всё, вопросов больше нет. Ваши же ответы были неадекватны вопросу.
Цитата: Dobryаk
От замечания о строгой электронейтральности атома с неподвижным ядром и релятивистскими электронами Вы просто отмахнулись... Звезда от атома не отличается ничем... В уравнения Максвелла для макроскопичеких полей --- я не понял, они у Вас тоже в категории ошибок 19-во века или нет? --- в правой части входят макроскопические заряд и ток. Если звезда ненамагниченная, счтайте ток нулевым. Остался заряд, который тоже нуль нуликом.
Уравнения Максвелла у меня тоже в категории ошибок. Я об этом с самого начала писал. Как и о том, что ТО и квантовая механика являются следствиями именно этих исходных ошибок математики физики.
Цитата: Dobryаk
Напоследок: мне пришлось отдуваться за ту пару конкретных "Писем трудящихся", где война был объявлена именно Лиенару с примкнувшим Вихертом, не надо мои слова ошибочно интерпретировать. Но от других сотрудников знаю, что война с этими космополитами была в большой моде. К сожалению, в своем подходе Вы мало чем отличаетесь от этой армии ниспровергателей основ...
Уйти из этого раздела даже заради Вашего удовольствия не могу. И не уйду.
Я пока свою теорию полностью не изложил. Сказал только про некоторые принципы - использование большего числа переменных, в частности, для описания волн от движущегося источника. Закончу - можно будет судить.
Об уходе из раздела речи не было. Я говорил о ветке - это Вы заявили, что больше в этой ветке не появитесь. Я Вас не гнал и не гоню - но огульные заявления мне не интересно слушать. Конкретные замечания готов выслушать - типа, как я уже сказал, здесь-то и здесь-то такие-то ошибки.
Еще общее замечание - я обсуждаю самые основы физики, самые первые шаги, самые, если хотите, примитивные ее элементы, кирпичики. Я пытаюсь объяснить, в чем я вижу ошибки в этих основах, допущенные, скажем, во времена Ньютона, Гука, Эйлера, Пуассона, Дюамеля. И язык, и аппарат должны быть соответствующими этим самым исходным понятиям. Обращаться же сейчас к самым верхним этажам физики в данной дискуссии я считаю просто бессмысленным. Потому что - для меня, по крайней мере, - это всё, вполне вероятно, всего лишь эпициклы на эпициклах, и разбираться в них у меня просто нет желания. Для меня вся современная физика после Максвелла просто не существует. Вы, разумеется, в нее верите - а я нет. Потому у нас действительно нет общего фундамента для разговора (впрочем, когда я говорил об электрическом поле электронов в звезде, я говорил об этом в рамках ТО и общий фундамент был, временно).
Я говорю о построении новой матфизики. Где волновые уравнения нелинейны, принцип суперпозиции не выполняется, векторные поля нельзя разделить на соленоидные и безвихревые компоненты. И многое другое.
Насколько мне это удастся - увидим, когда я изложу это. Хотите участвовать - пожалуйста. Не хотите - не надо.
- +0.00 / 0
-

Москва
25 лет
Карма: +0.16
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: Dobryаk
Мне понятен интересен публики к ниспровержению этзой непонятной им науки --- все книги взять бы да и сжечь! --- но мне искренне досадно, что все это красуется в этом разделе ГА.
В данной ветке Вы являетесь обычным участником, а не модератором. У нас заранее была договоренность с ConstB - и с Вами персонально - что модерировать эту ветку буду только я. Так что никакой ответственности за ее содержание Вы не несете и показываться Вам здесь незачем.
Наука же, к Вашему сведению, развивается не прямолинейно. Время от времени происходит смена парадигмы. Современная физика является наукой ровно в той же степени, что и теория Птолемея с эпициклами, и теория теплорода (эти две - вполне научные теории). Рано или поздно она будет заменена другими теориями (и это большой вопрос, сколь многое из нынешней физики сохранится).
Физика развивалась очень быстро в 18-19 веках, когда была свобода высказывать любые гипотезы и теории. Сейчас же в физике опять существует почти столь же жесткая система научной цензуры, как и в средневековье, и опубликовать что-либо новое в научных журналах (физических) стало невозможным. Заметно, как Вас раздражает, что сейчас в интернете можно опубликовать что угодно, или что в конце 80-х в СССР стали публиковать много "еретических" книг.
Но именно среди этих еретических теорий можно ожидать найти те, которые сформируют новую физику. Пусть даже 99.99% из них являются ерундой. Кроме того, история науки показывает, что почти все действительно революционные теории вначале категорически отвергались адептами "нормальной науки" и только потом, постепенно получили признание - у следующего поколения ученых. Смена научных парадигм происходит со сменой поколений ученых (Планк). Точнее, происходила - до внедрения жесткой научной цензуры.
Эта ветка - альтернативная наука. Не только физика. Я вначале хотел говорить о других науках и только в конце перейти к физике. Но в итоге начал все же с физики. Я, кроме того, сразу предупредил (всех модераторов и персонально Вас, в личном письму), что я собираюсь говорить о "ненаучных" вопросах с точки зрения науки: таких как религии, инопланетяне и пр. Вы сказали, что у Вас нет возражений насчет того, чтобы это было в научном разделе и чтобы модерировал свою ветку только я сам. Сейчас же - еще задолго до того, как я дошел до "ненаучных" вопросов - Вам уже стало "искренне досадно, что все это красуется в этом разделе ГА."
Это - не Ваша ответственность. Это - не Ваш личный раздел. Наука не ограничивается теми рамками, которые Вам лично кажутся единственно возможными.
P.S. В конце недели я просмотрю ветку и очень сильно сокращу и удалю ряд сообщений, своих и чужих. В частности, наши с Вами препирательства.
- +0.00 / 0
-

Козлодоевск
25 лет
Карма: +19.43
Регистрация: 26.04.2011
Сообщений: 345
Читатели: 0
Регистрация: 26.04.2011
Сообщений: 345
Читатели: 0
Цитата: Yuri Rus от 07.06.2011 18:12:04
Наука не ограничивается теми рамками, которые Вам лично кажутся единственно возможными.
Юрий, мне хотелось бы Вас поддержать.
Насколько я понимаю, Вы хотели бы апробировать Вашу теорию в более-менее неформальной обстановке, без официоза. Поскольку официоз немедленно пустит в ход огульные отрицания типа «ЭТОГО НЕ МОЖЕТ БЫТЬ ПОТОМУ, ЧТО НЕ МОЖЕТ БЫТЬ НИКОГДА!» и вешание ярлыков типа "Это антинаучно!" "Это лженаука!" и "Это бред!"
Гносеологически Вы совершенно правы, развитие идет не равномерно и прямолинейно, а некими скачками. Нужно пытаться создавать что-то новое и ранее не виданное, иначе - застой и смерть.
И даже если выяснится, что Вы неправы, Ваша попытка будет заслуживать величайшего уважения, потому что её альтернатива - бронзоветь в уютненьком болотце.
Прошу Вас, продолжайте.
История: Описание, чаще всего лживое, действий, чаще всего маловажных, совершенных правителями, чаще всего плутами, и солдатами, чаще всего глупцами. (с) Амброз Бирс, "Словарь Сатаны"
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: ABahus от 07.06.2011 20:50:38
Юрий, мне хотелось бы Вас поддержать.
Насколько я понимаю, Вы хотели бы апробировать Вашу теорию в более-менее неформальной обстановке, без официоза. Поскольку официоз немедленно пустит в ход огульные отрицания типа «ЭТОГО НЕ МОЖЕТ БЫТЬ ПОТОМУ, ЧТО НЕ МОЖЕТ БЫТЬ НИКОГДА!» и вешание ярлыков типа "Это антинаучно!" "Это лженаука!" и "Это бред!"
Гносеологически Вы совершенно правы, развитие идет не равномерно и прямолинейно, а некими скачками. Нужно пытаться создавать что-то новое и ранее не виданное, иначе - застой и смерть.
И даже если выяснится, что Вы неправы, Ваша попытка будет заслуживать величайшего уважения, потому что её альтернатива - бронзоветь в уютненьком болотце.
Прошу Вас, продолжайте.
Спасибо.
Добряк удалил все свои посты в ветке; хорошо. Я написал письмо модераторам Научно-Технического раздела и ConstB, что я не хочу, чтобы Добряк имел права модерации в моей ветке. Свое мнение он может иметь, но не должен иметь права запрещать и не пущать. Если надо, пусть эта ветка будет перенесена в Пользовательские, меня это не волнует. Правда, все модераторы Научно-Технического раздела, включая Добряка, одновременно являются и модераторами пользовательских, плюс еще несколько человек.
Я буду продолжать только при условии, что модерировать эту ветку буду только я один. На всякий случай, вот о чем я собираюсь писать в будущем:
Здесь и здесь я написал модераторам, о чем я планирую писать на своей ветке.
Я не хочу тратить свое время, чтобы потом увидеть, что Добряк или кто-то еще решил, что это лже-наука и делетировал это.
- +0.00 / 0
-

64 года
Карма: +401.03
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 3,937
Читатели: 2
Модератор ветки
Цитата: mozgi
Я вот никак понять не могу, чего орать то благим матом что вас тут зажимают. Условия тут какието выдвигаете. Добряк вас тут что, нещадно удалял, или рот затыкал? Он же ни разу не воспользовался своим правом модерировать. Человек отстаивает свою позицию и пытается вам доказать, что вы не правы. Вот уже и почитатели ваших работ, из которых мы имели счастье узреть только введение, кричат что злые ученые все скрывают и огульно обвиняют. Я в упор не видел здесь, чтобы хоть кто-то орал что это все вранье и огульно все отрицал. Вы же сами в своих же выкладках путаетесь беспрерывно, и как только, кто-то тыкнет пальцем в нестыковки в ваших же рассуждениях или вычислениях, тут же говорите что это на самом деле неважно. А коли неважно, зачем это все постить тогда? Как только возникают неудобные вопросы - вы от них отмахиваетесь, да еще и удалить все хотите. Я еще раз повторю, ведите дискуссию по-человечески. А то выглядит, как минимум, смешно, сплошные передергивания и виляния.
P.S. АУ потому что не по теме, но это в самом деле уже переходит все границы. Я, Я, Я, Ветка моя, никто сюда не ходите, только я буду тут писать. кого хочу буду удалять.
mozgi, я пока еще ни чьи сообщения не удалял. С Вами я разговаривать не хочу, потому что пришел к выводу, что Вы тролль, и предупреждал, чтобы Вы здесь не появлялись. Но раз Вы поставили свое сообщение на АУ, отвечу один раз.
Удалить я хочу большую часть дискуссии, которая последовала в результате моей небрежности, потому что написано слишком много. Я оставлю небольшую часть, где будет сформулировано, что я в данном случае ошибся. Но я не вижу смысла заставлять будущих посетителей ветки читать всю эту длинную дискуссию и пытаться уследить за аргументами, чтобы в конце увидеть, что это все зря.
Это знак уважения к читателям, не более того. Не заметание следов своих ошибок.
Отредактировано: Yuri Rus - 09 июн 2011 в 01:55
- +0.00 / 0
-

Карма: +113.64
Регистрация: 15.10.2008
Сообщений: 1,034
Читатели: 0
Регистрация: 15.10.2008
Сообщений: 1,034
Читатели: 0
Юрий, Добряк, к сожалению, слишком эмоционален там, где не нужно. Ему бы холодный ум включить, а не горячее сердце, было бы больше пользы, всем.
Я, может быть, вперед забегаю, но у меня вопрос - как ваша теория согласуется с теорией Ритца, которая объясняет очень много эффектов, наблюдаемых в космосе (цефеиды, сверхновые и т.п.) на основе механики Галилея (эффекта Ритца) без всех этих заумей типа ОТО и СТО?
Я, может быть, вперед забегаю, но у меня вопрос - как ваша теория согласуется с теорией Ритца, которая объясняет очень много эффектов, наблюдаемых в космосе (цефеиды, сверхновые и т.п.) на основе механики Галилея (эффекта Ритца) без всех этих заумей типа ОТО и СТО?
- +0.00 / 0
-
Сейчас на ветке:
2,
Модераторов: 0,
Пользователей: 0,
Гостей: 0,
Ботов: 2