Жизнь, Разум, Человек, Религия и Наука
149,880
565

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: wow от 21.05.2011 12:36:07
Не могу не согласиться с Поверонов, что физика есть суть упрощение, модель реальности, более или менее адекватно пытающуюся описать эту реальность, дабы суметь предсказать поведение оной, согласно нарисованной модели и, соответственно, попользоваться полезным эффектом. И говорить, что в описаниях модели содержаться ошибки,т.к. она несколько неверно описывает реальность, по крайней мере, абсурдно. Само понятие модель и предполагает, что мы преднамеренно упростили реальность, введя некоторые абстрактные понятия, как то: сила, энергия, импульс, волна и т.п. ,(которых в реальности нет, как правильно писал mozgi, есть только возмущения и взаимодействия).
По мере развития, модели уточняются, достигают некоторого предельного уровня, когда пора вводит новый уровень абстракций, старая модель (зарекомедовавшая себя на протяжении веков, а значит на этом уровне приближения абстракции верно описывающая реальность) отнюдь не отбрасывается, а просто становится частным случаем модели более высокого уровня.
Так что громкое заявление «что одной из важнейших внутренних причин грядущей катастрофы является глубокая ошибочность современной физики» ,каГбы наводит на определеные мысли, самая безобидная из которых, что вы не понимаете суть, философию развития жизни. Если бы Вы предложили качественно новую, более высшую ступень абстракции (например, как эту, куда все современное здание науки войдет частным случаем, при определенных допущениях, то честь Вам и хвала, а так ,увы,Вы пытаетесь одну модель современного здания науки, которая уже зарекомендовала себя реальными результатами, заменить своей моделью, у которой лишь громкие заявления. Не более.
Про эпициклы Вам уже ответили. Но есть и другие примеры - например, на протяжении не веков, а тысячелетий, жрецы предсказывали разливы рек (Нила, напр.), приход весны, сезона дождей и пр., используя свои собственные модели мироздания. Их модели - работали, то есть позволяли делать практические предсказания, которые подтверждались экспериментами.
Это весьма распространенная среди физиков точка зрения, что уравнения современной физики в основном верны и все последующие более общие теории обязаны включить нынешнюю физику как частный случай. Подобно тому, как Ньютоновская механика входит в теорию относительности или квантовую механику. На самом деле, это весьма самонадеянно.
Если разобраться, физики убеждены в справедливости своей нынешней картины мира в основном потому, что она очень сложная, со множеством формул, тонких эффектов, с высокой точностью экспериментов. Точно так же, как последователи Птолемея были убеждены в справедливости геоцентрической модели - тоже очень сложной и точной. Модель Коперника вначале уступала модели Птолемея по всем этим параметрам - и по точности, и по сложности. И тем не менее - вся эта цветущая сложность оказалось ложной. Ничего этого в реальности не существовало.
Цитата: wow от 21.05.2011 12:36:07
Непонятен так же смысл «простыней» на сугубо политико-экономическом форуме, ведь в сети полно чисто физических форумов, где, я думаю, найдутся истинные физики, понимающие досконально не только сами эти формулы, но и то, что это лишь суть абстракции, допущения, математические модели и искать в них ошибки, тоже самое, что возмущаться, почему облака не правильные конусы и элипсы, хотя формулы говорят, что они должны быть такими. И даже сугубо по теории относительности полно форумов, где все эти парадоксы масс и близнецов постоянно жуются. Вот и выложите там свое откровение: "Я считаю, что теория относительности неверна...Теория относительности постулирует, что движение быстрее скорости света невозможно и что по мере приближения скорости космического корабля к скорости света его масса будет стремиться к бесконечности», может найдутся понимающие люди, которые объяснят Вам, что теория относительности, постулирующая бесконечность массы при световой скорости это одно, а реальность несколько иное, и в ней ни какой бесконечной массы не будет, и ниспровергать основ физики Вам не придеться.
Разговор на тему о моей физической теории начался на ветке Вселенная, жизнь, разум... Сначала я не предполагал писать здесь о физике, тем более с обилием формул, но несколько участников форума предложили мне все-таки написать об этом, поскольку здесь есть довольно много людей с физическим образованием и они вполне способны оценить мои идеи. Чтобы мои слова не выглядели голословными, пустым хвастовством, я в итоге согласился. Сначала я планировал писать здесь в основном на темы (см. название ветки) Жизнь, Разум, Человек, Религия и Наука. Но начал все-таки с физики - как сказано во втором сообщении ветки, из-за перехода мирового кризиса в горячую фазу.
На других, физических форумах, я позже тоже выложу свои тексты.
Цитата: wow от 21.05.2011 12:36:07
И что у Вас, так все утилитарно: :)"Ресурсы сначала Солнечной системы, затем других звездных систем будут доступны людям – и перевозка тяжелых грузов (металлов и пр.) от дальних звезд будет вполне рентабельна», возить, ресурсы, что бы делать очередной виток потреблятсва. А как насчет психофизического посещения других планет, без всяких полетов громоздких железок, посредством тонкой субстанции человека. Как насчет развития по пути не роста потреблятсва, все увеличивающегося населения, а как осознанная жизнь в согласии с природой и космосом.
Ну что поделать. Вот такой я приземленный человек. Забочусь не столько о путешествиях тонких субстанций по Вселенной, сколько о выживании человечества прямо сейчас, в ближайшие годы и десятилетия, и о полете к звездам грубых материальных тел людей. Можете назвать это и потреблятством.

Карма: +2.39
Регистрация: 26.10.2008
Сообщений: 1,224
Читатели: 3
Регистрация: 26.10.2008
Сообщений: 1,224
Читатели: 3
Yuri Rus, я просмотрел Вашу ссылку. Ну что ж, излагайте, желательно научно-популярно, как просили некотрые камрады. . Просто уж такие заявы(с той ветки): "P.S. Я всего лишь утверждаю, что теория Максвелла неверна. Как следствие - неверна теория относительности (СТО и ОТО), а также вся современная космология (Big Bang etc.). Неверна квантовая механика. Частично - неверны оптика и акустика", смотрятся уж очень ,( мягко говоря), экстравагантно. Как говориться факты в студию. Вот Поверонов пишет: " В принципе всякая теория, дающая те же расчетные значения, что и проверенные экспериментально, ничем не хуже общепринятой, а может быть и лучше, если дает интересные и полезные следствия.". Здесь ключевое слово полезные.
. Просто уж такие заявы(с той ветки): "P.S. Я всего лишь утверждаю, что теория Максвелла неверна. Как следствие - неверна теория относительности (СТО и ОТО), а также вся современная космология (Big Bang etc.). Неверна квантовая механика. Частично - неверны оптика и акустика", смотрятся уж очень ,( мягко говоря), экстравагантно. Как говориться факты в студию. Вот Поверонов пишет: " В принципе всякая теория, дающая те же расчетные значения, что и проверенные экспериментально, ничем не хуже общепринятой, а может быть и лучше, если дает интересные и полезные следствия.". Здесь ключевое слово полезные.
 . Просто уж такие заявы(с той ветки): "P.S. Я всего лишь утверждаю, что теория Максвелла неверна. Как следствие - неверна теория относительности (СТО и ОТО), а также вся современная космология (Big Bang etc.). Неверна квантовая механика. Частично - неверны оптика и акустика", смотрятся уж очень ,( мягко говоря), экстравагантно. Как говориться факты в студию. Вот Поверонов пишет: " В принципе всякая теория, дающая те же расчетные значения, что и проверенные экспериментально, ничем не хуже общепринятой, а может быть и лучше, если дает интересные и полезные следствия.". Здесь ключевое слово полезные.
. Просто уж такие заявы(с той ветки): "P.S. Я всего лишь утверждаю, что теория Максвелла неверна. Как следствие - неверна теория относительности (СТО и ОТО), а также вся современная космология (Big Bang etc.). Неверна квантовая механика. Частично - неверны оптика и акустика", смотрятся уж очень ,( мягко говоря), экстравагантно. Как говориться факты в студию. Вот Поверонов пишет: " В принципе всякая теория, дающая те же расчетные значения, что и проверенные экспериментально, ничем не хуже общепринятой, а может быть и лучше, если дает интересные и полезные следствия.". Здесь ключевое слово полезные.
Отредактировано: wow - 21 май 2011 21:19:04
59 лет
Карма: +173.90
Регистрация: 20.09.2008
Сообщений: 15,636
Читатели: 11
Регистрация: 20.09.2008
Сообщений: 15,636
Читатели: 11
Цитата: Yuri Rus от 21.05.2011 19:45:13
Я бы рад не вводить новые сущности, но ведь учебники-то по физике пока не переписали, а потому мне надо как-то объяснить разницу между принятым в физике понятием полного дифференциала и более общим понятием, которое я ввожу.
Да не вводите вы нового.. вы переводите то, что было параметром модели в переменную, создавая новую, более сложную модель. Не вводите новых сущностей там, где их нет.
Цитата: Yuri Rus от 21.05.2011 19:45:13 Но пытаюсь показать, что многие принятые в мат. физике понятия и формулы неверны. Дело в том, что мат. физика имеет блочную структуру. Однажды выведенная формула, после первого периода критики и экспериментальной проверки, становится "блоком", кирпичом в строительстве следующих этажей физики. В дальнейшем, эта формула просто считается истинной и ее применяют для вывода каких-то других формул, более не подвергая ее саму сомнению. Примеры: Второй Закон Ньютона, Второй Закон Термодинамики и Принцип Неопределености Гейзенберга. Их просто применяют, как инструменты решения каких-то новых физических задач, почти никогда не ставя вопрос о том, справедливы ли сами эти законы и если да, то в какой области параметров.
Вы путате модели, которые имеют ограниченную область применимости (то что Вы называете "формулы") и понятия.
Цитата: Yuri Rus от 21.05.2011 19:45:13
... Чтобы распутать этот детектив, я и начал с анализа единичных vs. полных функций, дифференциалов и волн. Особую роль, по моему мнению, сыграли ошибки в анализе линейного неоднородного волнового уравнения с движущимся источником. Поэтому я уделяю этому уравнению основное внимание.
Всё верно - принцип суперпозиции выполняется только для линейного однородного волнового уравнения. Но не для неоднородного - и в особенности он не выполняется для движущегося источника. Это как раз я и считаю главной ошибкой мат. физики.
Сознательное упрощение модели, чтобы получить достаточные (на момент создания упрощенной модели) результаты делается сознательно (хотя при этом выглядит типа "а выкинем тот небольший член, который не можем аналитически посчитать" довольно волюнтаристски) и "главной ошибкой матфизики" не является. Это сознательно сделанное упрощение. Вы можете столь-же сознательно его не делать и продвинуться на шаг дальше или упереться в недостаточность мат. аппарата и будете вынуждены упрощать модель...
Толерантность - термин, означающий невозможность организма распознавать инородные клетки.
Западная борьба с коррупцией в России - борьба за легальную куплю-продажу власти иностранными агентами.
Честность, Справедливость, Состоятельность
Западная борьба с коррупцией в России - борьба за легальную куплю-продажу власти иностранными агентами.
Честность, Справедливость, Состоятельность

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: BUR от 23.05.2011 16:31:18Да не вводите вы нового.. вы переводите то, что было параметром модели в переменную, создавая новую, более сложную модель. Не вводите новых сущностей там, где их нет.
Вы путате модели, которые имеют ограниченную область применимости (то что Вы называете "формулы") и понятия.
Сознательное упрощение модели, чтобы получить достаточные (на момент создания упрощенной модели) результаты делается сознательно (хотя при этом выглядит типа "а выкинем тот небольший член, который не можем аналитически посчитать" довольно волюнтаристски) и "главной ошибкой матфизики" не является. Это сознательно сделанное упрощение. Вы можете столь-же сознательно его не делать и продвинуться на шаг дальше или упереться в недостаточность мат. аппарата и будете вынуждены упрощать модель...
Мне, честно говоря, стало непонятно, о чем мы спорим. Сначала вроде разговор шел о том, что мне не было необходимости вводить новые сущности (я понял так, что Вы имели в виду новые термины - единичный vs. полный дифференциалы, и ответил, что без нового термина пока что не обойтись), потому что то, что я пишу, вполне в рамках мат. физики, просто то, что раньше считалось параметрами, я считаю полноценными переменными. Сейчас же, если я правильно Вас понял, Вы утверждаете, что переводя некую величину, которая в более ранних моделях считалась параметром, в статус полноценной переменной, мы получим новую, более полную модель, но старая модель при этом все равно останется справедливой (в своей области параметров). Более того, Вы утверждаете, что более ранние модели (с параметрами вместо переменных) делали это упрощение сознательно. И это не является "главной ошибкой мат. физики" - если же усилить Вашу мысль, то это вообще не является ошибкой, просто "старая" модель имеет свою область применимости, где она справедлива (так большинство формул физики имеют ограниченную область применимости, это нормально).
Вообще-то, главной ошибкой мат. физики я называл не это, а неправильное решение неоднородного волнового уравнения (до детального объяснения того, в чем же здесь ошибка, я пока так и не дошел; но дойду). Теперь, насколько важно это различие - параметр или переменная. На первой странице ветки, я приводил цитаты из книг Leigh Page и Petr Beckmann, в которых на основании определения полного дифференциала, зависящего только от переменных x, y, z и t, выводилось сжатие поля и частиц в гамма раз. То есть, неверное (как я считаю) понимание того, что является параметром, а что переменной, привело к тому, что физика более чем на столетие погрузилась в бесплодную схоластику. Я сейчас как раз нашел подобную аргументацию на русском языке (на первой странице ветки я спрашивал, не встречал ли кто что-то подобное на русском; но теперь заменить текст Leigh Page я не могу, потому что цитирую его много раз). Более того, в данной книге на этом аргументе (то есть на определении полного дифференциала) построен весь вывод теории относительности, ее обоснование. Так что, для целей демонстрации важности понимания того, сколько же у нас переменных, эта книга еще лучше.
Итак, Беккер Р. «Теория Электричества. Том 2. Электронная теория» (1941), стр. 44, 48-52:






И так далее - потом выводятся все остальные уравнения ТО. Подчеркиваю – выводятся из неправильного определения того, сколько переменных имеется в уравнениях для электрического и магнитного полей (или потенциалов φ и A).
Но дело обстоит еще интереснее. Даже если в уравнениях физики некоторые величины явным образом вводятся как переменные (а не параметры), к ним все равно не относятся как к переменным (например, их частные производные все равно не входят в полный дифференциал соответствующей функции; по ним не дифференцируют и не интегрируют).
В физике есть такое понятие – функции Грина. Если посмотреть на функции Грина для волнового уравнения с движущимся источником, то, безусловно, они выглядят очень близкими по смыслу к тому, о чем писал я.
Джексон Дж. «Классическая электродинамика» (1965), стр. 209-212:




Казалось бы, векторы x, из начала координат к произвольной точке пространства (x, y, z) в момент времени t, и x', из начала координат к источнику (x’, y’, z’) в запаздывающий момент времени t’, являются точно такими же переменными, как у меня (x, y, z), для произвольной точки пространства в момент t, и (ξ, η, ζ), для положения источника в момент ԏ. Что еще нужно?
И тем не менее, разница есть, и существенная. Я говорю, что все 6 пространственных координат и 2 временные являются переменными и относиться к ним надо соответственно. Например, включать их частные производные в определение полного дифференциала и полной производной по времени. Например, интегрировать по всем 6 пространственным координатам, а не только по 3 из них; по 2 временным координатам, а не по одной. Между прочим, для запаздывающих функций обычно интегрируют по запаздывающим координатам источника и по запаздывающему времени, а не по координатам точки наблюдения в настоящий момент времени. При этом, координаты (x, y, z) и время t вообще не учитываются (они являются параметрами, в Вашей трактовке?). А если речь идет о сравнении "замороженного" поля частицы в точке (x, y, z) в момент t и в точке (x + vdt, y, z) в момент t + dt, то внезапно забывают про переменные координаты (x', y', z' ) и время t' и перепрыгивают на x, y, z, t.
Это всё имеет совсем другой математический смысл – и приводит совсем к другим результатам. Главное здесь то, что эти результаты не «расширяют» старые модели на новые области применения, а отменяют старые результаты – вообще.
Отредактировано: Yuri Rus - 02 дек 2019 03:25:50

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Примечание: я пользуюсь Firefox и он показывает все формулы нормально. Но сейчас я глянул на формулы в Google Chrome и Internet Explorer и обнаружил, что по крайней мере одну букву они оба не показывают (нижний индекс маленькую а):
pₐ = pa
Если есть возможность, лучше смотреть в Firefox.
-------------------------
Сейчас я собираюсь обсудить вопрос о выводе преобразований Лоренца. Однако, если я сразу начну говорить о движении электрического заряда и волновом уравнении для электростатического потенциала φ, во-первых, возникнет впечатление, что это относится только к волнам, распространяющимся со скоростью света. Во-вторых, это будет не очень очевидно, потому что «пощупать пальцами» явления, происходящие со скоростью света, нельзя. Как следить за динамикой распространения таких волн, за промежуточными этапами? Даже измерить скорость света в одном направлении – и то нельзя; можно только туда и обратно. Кроме того, все слишком привыкли к идее, что скорость света играет особенную роль, там всё по-другому. Поэтому я решил начать со звуковых волн, как более наглядных, понятных, которые сравнительно медленные и процесс распространения которых можно наблюдать в динамике. А потом уже мы применим полученные результаты к движущимся зарядам и сравним с тем, что говорит общепринятая физическая теория.
Формул будет довольно много, но они очень простые. Единственная трудность – форма записи, в одну линию, со множеством скобок. Я не хочу переводить каждую формулу в jpg формат, это займет слишком много времени. А иного способа дать формулы на форуме в привычном виде я не знаю. Хорошо хоть, нашел возможность делать subscript и superscript индексы маленькими цифрами и некоторыми буквами (а то было бы, допустим, ∂2u/∂t2, а не ∂²u/∂t²).
Начну я с «нулевого приближения» – это означает, что последовательные волны от движущегося источника не взаимодействуют; каждая единичная волна распространяется радиально с фазовой скоростью с в покоящейся среде. Рассмотрим движущийся источник звуковых волн (продольных) в жидкости. Здесь есть такая проблема. Я уже говорил, что решение Дюамеля неоднородного волнового уравнения неверно. Кроме того, само волновое уравнение в случае наличия источника должно записываться совсем не так:
∂²u/∂t² – c²∇²u = S(x, y, z, t)
В нем должны присутствовать координаты источника (ξ, η, ζ) и время излучения единичной волны ԏ. Я пока не хочу вводить это более сложное уравнение. Я хочу показать, что к выводам об ошибочности волнового уравнения (и как следствие – почти всей физики) можно прийти даже в рамках существующего математического аппарата физики. Мне кажется, большинству читателей будет легче понять, в чем заключаются эти ошибки, если изложение не будет привязано к новому мат. аппарату, если мы будем пользоваться привычным математическим языком «старой» физики. Потом уже можно говорить и о новом мат. аппарате.
Достичь этой цели можно, если, вместо неоднородного, мы будем пользоваться однородным волновым уравнением
∂²p/∂t² – c²∇²p = 0,
где p – звуковое давление (разность между полным давлением и равновесным давлением в жидкости).
Это однородное уравнение действительно решено правильно (Д'Аламбером и Пуассоном), никаких претензий я не имею. И для него мы действительно можем обойтись лишь тремя пространственными координатами и одной временной – (x, y, z, t).
Пусть в момент времени t=0 среда покоится, причем p и dp/dt равны нулю везде, кроме точки (0, 0, 0), где находится источник. Источник не точечный, он представляет собой сферу радиуса a. Обозначим давление на поверхности этой сферы как pₐ(t). В нулевой момент времени оно равно pₐ(0) – некое давление, которое мы выбрали. Мы можем найти решение этого однородного уравнения, пользуясь формулой Пуассона (см. цитаты из книги Кошлякова и др. на второй странице ветки). Это – единичная сферическая волна, распространяющаяся со скоростью с, центром которой является точка (0, 0, 0). Мы также можем описать распространение этой волны при помощи более простого уравнения:
r₁(t) = ct = i x(t) + j y(t) + k z(t)
где с – вектор скорости звука; r₁(t) – радиус-вектор первой единичной волны: x(t), y(t), z(t) – координаты какой-то точки на этом фронте в момент времени t.
r₁(t) = (x²(t) + y²(t) + z²(t))½
В СО покоящейся среды, последовательные стадии распространения одной единичной волны в разные моменты времени выглядит следующим образом:
Здесь и везде, когда я использую термин «единичная волна», имеется в виду маленький кусочек волны, излученной за промежуток времени dt. Этот термин имеет совсем другой смысл, чем волна длительностью λ с периодом 2π. Пардон, если это внесло путаницу в мои предыдущие сообщения.
За время dt источник сместился в точку (v dt, 0, 0), и давление на его поверхности стало pₐ(dt). Мы можем найти решение этого уравнения, опять пользуясь формулой Пуассона, причем опять полагая, что вся остальная среда покоится. Распространение второй единичной волны подчиняется закону:
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Затем мы можем найти решение для распространения единичной сферической волны, излученной в момент времени 2dt, из следующей точки – (2v dt, 0, 0).
r₃(t) – i 2v dt = c(t – 2dt)
(x(t) – 2v dt)² + y²(t) + z²(t) = c² (t – 2dt)²
И так далее. В СО покоящейся среды, мгновенный снимок последовательных единичных волн выглядит так:
В СО движущегося источника, эта же картинка описывает как распространение единичной волны в разные моменты времени, так и мгновенный снимок последовательных фронтов волн.
Этот подход с единичными волнами, каждая из которых описывается однородным волновым уравнением, очень похож на описание проблемы излучения из книги Куранта «Методы математической физики», т. 2, стр. 191 (уже цитированной на второй странице ветки):

Пара слов о терминах. Сила, действующая на элемент объема ΔV, пропорциональна градиенту давления:
ΔF = – ∇p ΔxΔyΔz
Это уравнение очень похоже на уравнение для силы гравитации F как градиента гравитационного потенциала φ
F = – m ∇φ
и уравнение для силы электростатического взаимодействия двух зарядов как градиента электростатического потенциала φ
F = – q ∇φ = q E
E = – ∇φ
Для гравитации, φ m, и для электростатики, φ q, имеют размерность энергии и представляют собой потенциальную энергию. Аналогично, p ΔV имеет размерность энергии и представляет собой часть потенциальной энергии жидкости или газа (напомню, что энтальпия H = U + pV, внутренняя энергия плюс давление, умноженное на объем). Давление, таким образом, это удельная потенциальная энергия (часть оной): потенциальная энергия, разделенная на единицу объема. Зачем я это подчеркиваю? Затем, что есть такое часто используемое понятие как «эквипотенциальные поверхности», и все привыкли, что сила перпендикулярна этим поверхностям. Тогда как понятие «поверхности равного давления» используется намного реже и, мне кажется, если я стану его применять, читателям будет не настолько очевидно, что сила давления должна быть перпендикулярна этим поверхностям. Так что я буду в дальнейшем, говоря об эквипотенциальных поверхностях, иметь в виду поверхности равного давления. В данном случае, они имеют один и тот же смысл.
Далее, напомню определение: «ФРОНТ ВОЛНЫ - поверхность, окружающая источник колебаний, все точки которой имеют одинаковые фазы колебаний. Фронт волны может быть сферой (сферическая волна) или иметь более сложную форму». Понятие единичной волны, которым я здесь пользуюсь, в принципе, совпадает с понятием фронта волны.
В статическом случае, когда источник звуковых волн неподвижен, каждый фронт волны совпадает с сферической эквипотенциальной поверхностью – давление во всех точках любого фронта одинаково. Сила направлена по нормали к поверхности фронта волны – радиально (сила, по определению, направлена по нормали к эквипотенциальной поверхности).
Сделаем предположение, что при движении источника фронт каждой волны тоже совпадает с эквипотенциальной поверхностью, то есть давление во всех его точках одинаково и сила направлена по нормали к поверхности фронта волны. Возможно, это предположение выполняется не всегда или вообще не выполняется, тогда в будущем мы его скорректируем. Сейчас же построим модель распространения звуковых волн, исходя из этого предположения.
Это означает, что в любой момент времени давление в каждой точке какой-либо единичной волны одинаково – если одинаково давление на всей поверхности источника pₐ(t). А это давление определяется внешней силой, которую мы задаем сами. Примем, что внешняя сила одинакова на поверхности источника – значит, будет одинаковой.
Тогда при распространении первой единичной волны, излученной в момент времени 0 из точки (0, 0, 0), давление в каждой ее точке будет меняться по закону:
p₁(x, y, z, t) = pₐ(0) a / r₁(t) = pₐ(0) a / (ct)
Давление в каждой точке второй единичной волны будет меняться по закону:
p₂(x, y, z, t) = pₐ(dt) a / |r₂(t) – v dt| = pₐ(dt) a / (c (t – dt))
Третьей:
p₃(x, y, z, t) = pₐ(2dt) a / |r₃(t) – 2v dt| = pₐ(2dt) a / (c (t – 2dt))
Как я буду писать ниже, в электродинамике для потенциалов движущихся зарядов используется формула Лиенара-Вихерта, с дополнительным множителем 1 / (1 – r’∙v / (r’c)), таким же, как в уравнении Доплера. Но мы этот множитель сейчас вводить не будем. Он играет фундаментальную роль в рождении теории относительности и я буду очень долго о нем говорить немного позже. Пока же обойдемся без него.
Давайте еще более упростим нашу модель. Пусть длина волны λ (уже не единичной волны, а волны с периодом 2π) много больше, чем радиус a источника. Тогда, если нас интересуют волны вблизи от источника, мы можем считать, что за то время, когда волны проходят расстояние порядка нескольких десятков радиусов источника, величина pₐ практически не меняется: pₐ ≈ const. Пусть, далее, pₐ > 0, то есть сила, действующая на частицы среды, направлена от источника.
Еще раз посмотрим на эту картинку:
Согласно нашему предположению о совпадении фронтов волн с эквипотенциальными поверхностями, эти сферы – поверхности равного давления. Сила, как градиент давления, направлена по нормали к поверхности этих сфер. Проведем непрерывные силовые линии от источника таким образом, чтобы они были перпендикулярны всем этим сферам. Легко видеть, что силовые линии должны быть кривыми, причем загнутыми вперед, по направлению движения источника:
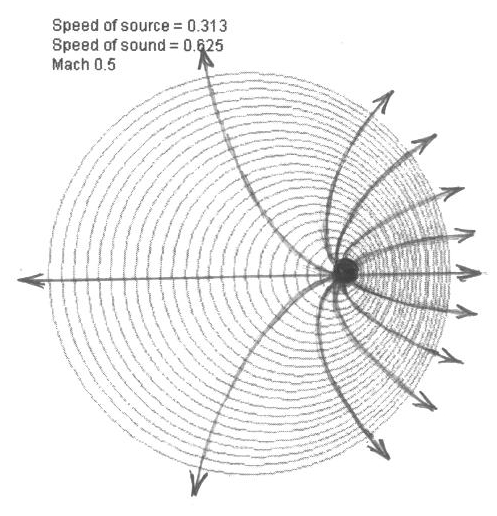
Если вы смотрите на эти силовые линии из СО покоящейся среды, в этом нет ничего удивительного, ведь это относится к последовательным единичным волнам, излученным из разных точек. Но напомню, что в СО источника так выглядят не только силовые линии, перпендикулярные фронтам последовательных единичных волн, но и силовые линии, перпендикулярные фронту одной и той же единичной волны в разные моменты времени. Обратите внимание, как сгущаются силовые линии перед источником: через единицу поверхности перед источником проходит намного больше силовых линий, чем сзади от него. Никакой симметрии «перед-зад» здесь и в помине нет.
pₐ = pa
Если есть возможность, лучше смотреть в Firefox.
-------------------------
Сейчас я собираюсь обсудить вопрос о выводе преобразований Лоренца. Однако, если я сразу начну говорить о движении электрического заряда и волновом уравнении для электростатического потенциала φ, во-первых, возникнет впечатление, что это относится только к волнам, распространяющимся со скоростью света. Во-вторых, это будет не очень очевидно, потому что «пощупать пальцами» явления, происходящие со скоростью света, нельзя. Как следить за динамикой распространения таких волн, за промежуточными этапами? Даже измерить скорость света в одном направлении – и то нельзя; можно только туда и обратно. Кроме того, все слишком привыкли к идее, что скорость света играет особенную роль, там всё по-другому. Поэтому я решил начать со звуковых волн, как более наглядных, понятных, которые сравнительно медленные и процесс распространения которых можно наблюдать в динамике. А потом уже мы применим полученные результаты к движущимся зарядам и сравним с тем, что говорит общепринятая физическая теория.
Формул будет довольно много, но они очень простые. Единственная трудность – форма записи, в одну линию, со множеством скобок. Я не хочу переводить каждую формулу в jpg формат, это займет слишком много времени. А иного способа дать формулы на форуме в привычном виде я не знаю. Хорошо хоть, нашел возможность делать subscript и superscript индексы маленькими цифрами и некоторыми буквами (а то было бы, допустим, ∂2u/∂t2, а не ∂²u/∂t²).
Начну я с «нулевого приближения» – это означает, что последовательные волны от движущегося источника не взаимодействуют; каждая единичная волна распространяется радиально с фазовой скоростью с в покоящейся среде. Рассмотрим движущийся источник звуковых волн (продольных) в жидкости. Здесь есть такая проблема. Я уже говорил, что решение Дюамеля неоднородного волнового уравнения неверно. Кроме того, само волновое уравнение в случае наличия источника должно записываться совсем не так:
∂²u/∂t² – c²∇²u = S(x, y, z, t)
В нем должны присутствовать координаты источника (ξ, η, ζ) и время излучения единичной волны ԏ. Я пока не хочу вводить это более сложное уравнение. Я хочу показать, что к выводам об ошибочности волнового уравнения (и как следствие – почти всей физики) можно прийти даже в рамках существующего математического аппарата физики. Мне кажется, большинству читателей будет легче понять, в чем заключаются эти ошибки, если изложение не будет привязано к новому мат. аппарату, если мы будем пользоваться привычным математическим языком «старой» физики. Потом уже можно говорить и о новом мат. аппарате.
Достичь этой цели можно, если, вместо неоднородного, мы будем пользоваться однородным волновым уравнением
∂²p/∂t² – c²∇²p = 0,
где p – звуковое давление (разность между полным давлением и равновесным давлением в жидкости).
Это однородное уравнение действительно решено правильно (Д'Аламбером и Пуассоном), никаких претензий я не имею. И для него мы действительно можем обойтись лишь тремя пространственными координатами и одной временной – (x, y, z, t).
Пусть в момент времени t=0 среда покоится, причем p и dp/dt равны нулю везде, кроме точки (0, 0, 0), где находится источник. Источник не точечный, он представляет собой сферу радиуса a. Обозначим давление на поверхности этой сферы как pₐ(t). В нулевой момент времени оно равно pₐ(0) – некое давление, которое мы выбрали. Мы можем найти решение этого однородного уравнения, пользуясь формулой Пуассона (см. цитаты из книги Кошлякова и др. на второй странице ветки). Это – единичная сферическая волна, распространяющаяся со скоростью с, центром которой является точка (0, 0, 0). Мы также можем описать распространение этой волны при помощи более простого уравнения:
r₁(t) = ct = i x(t) + j y(t) + k z(t)
где с – вектор скорости звука; r₁(t) – радиус-вектор первой единичной волны: x(t), y(t), z(t) – координаты какой-то точки на этом фронте в момент времени t.
r₁(t) = (x²(t) + y²(t) + z²(t))½
В СО покоящейся среды, последовательные стадии распространения одной единичной волны в разные моменты времени выглядит следующим образом:

Здесь и везде, когда я использую термин «единичная волна», имеется в виду маленький кусочек волны, излученной за промежуток времени dt. Этот термин имеет совсем другой смысл, чем волна длительностью λ с периодом 2π. Пардон, если это внесло путаницу в мои предыдущие сообщения.
За время dt источник сместился в точку (v dt, 0, 0), и давление на его поверхности стало pₐ(dt). Мы можем найти решение этого уравнения, опять пользуясь формулой Пуассона, причем опять полагая, что вся остальная среда покоится. Распространение второй единичной волны подчиняется закону:
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Затем мы можем найти решение для распространения единичной сферической волны, излученной в момент времени 2dt, из следующей точки – (2v dt, 0, 0).
r₃(t) – i 2v dt = c(t – 2dt)
(x(t) – 2v dt)² + y²(t) + z²(t) = c² (t – 2dt)²
И так далее. В СО покоящейся среды, мгновенный снимок последовательных единичных волн выглядит так:

В СО движущегося источника, эта же картинка описывает как распространение единичной волны в разные моменты времени, так и мгновенный снимок последовательных фронтов волн.
Этот подход с единичными волнами, каждая из которых описывается однородным волновым уравнением, очень похож на описание проблемы излучения из книги Куранта «Методы математической физики», т. 2, стр. 191 (уже цитированной на второй странице ветки):

Пара слов о терминах. Сила, действующая на элемент объема ΔV, пропорциональна градиенту давления:
ΔF = – ∇p ΔxΔyΔz
Это уравнение очень похоже на уравнение для силы гравитации F как градиента гравитационного потенциала φ
F = – m ∇φ
и уравнение для силы электростатического взаимодействия двух зарядов как градиента электростатического потенциала φ
F = – q ∇φ = q E
E = – ∇φ
Для гравитации, φ m, и для электростатики, φ q, имеют размерность энергии и представляют собой потенциальную энергию. Аналогично, p ΔV имеет размерность энергии и представляет собой часть потенциальной энергии жидкости или газа (напомню, что энтальпия H = U + pV, внутренняя энергия плюс давление, умноженное на объем). Давление, таким образом, это удельная потенциальная энергия (часть оной): потенциальная энергия, разделенная на единицу объема. Зачем я это подчеркиваю? Затем, что есть такое часто используемое понятие как «эквипотенциальные поверхности», и все привыкли, что сила перпендикулярна этим поверхностям. Тогда как понятие «поверхности равного давления» используется намного реже и, мне кажется, если я стану его применять, читателям будет не настолько очевидно, что сила давления должна быть перпендикулярна этим поверхностям. Так что я буду в дальнейшем, говоря об эквипотенциальных поверхностях, иметь в виду поверхности равного давления. В данном случае, они имеют один и тот же смысл.
Далее, напомню определение: «ФРОНТ ВОЛНЫ - поверхность, окружающая источник колебаний, все точки которой имеют одинаковые фазы колебаний. Фронт волны может быть сферой (сферическая волна) или иметь более сложную форму». Понятие единичной волны, которым я здесь пользуюсь, в принципе, совпадает с понятием фронта волны.
В статическом случае, когда источник звуковых волн неподвижен, каждый фронт волны совпадает с сферической эквипотенциальной поверхностью – давление во всех точках любого фронта одинаково. Сила направлена по нормали к поверхности фронта волны – радиально (сила, по определению, направлена по нормали к эквипотенциальной поверхности).
Сделаем предположение, что при движении источника фронт каждой волны тоже совпадает с эквипотенциальной поверхностью, то есть давление во всех его точках одинаково и сила направлена по нормали к поверхности фронта волны. Возможно, это предположение выполняется не всегда или вообще не выполняется, тогда в будущем мы его скорректируем. Сейчас же построим модель распространения звуковых волн, исходя из этого предположения.
Это означает, что в любой момент времени давление в каждой точке какой-либо единичной волны одинаково – если одинаково давление на всей поверхности источника pₐ(t). А это давление определяется внешней силой, которую мы задаем сами. Примем, что внешняя сила одинакова на поверхности источника – значит, будет одинаковой.
Тогда при распространении первой единичной волны, излученной в момент времени 0 из точки (0, 0, 0), давление в каждой ее точке будет меняться по закону:
p₁(x, y, z, t) = pₐ(0) a / r₁(t) = pₐ(0) a / (ct)
Давление в каждой точке второй единичной волны будет меняться по закону:
p₂(x, y, z, t) = pₐ(dt) a / |r₂(t) – v dt| = pₐ(dt) a / (c (t – dt))
Третьей:
p₃(x, y, z, t) = pₐ(2dt) a / |r₃(t) – 2v dt| = pₐ(2dt) a / (c (t – 2dt))
Как я буду писать ниже, в электродинамике для потенциалов движущихся зарядов используется формула Лиенара-Вихерта, с дополнительным множителем 1 / (1 – r’∙v / (r’c)), таким же, как в уравнении Доплера. Но мы этот множитель сейчас вводить не будем. Он играет фундаментальную роль в рождении теории относительности и я буду очень долго о нем говорить немного позже. Пока же обойдемся без него.
Давайте еще более упростим нашу модель. Пусть длина волны λ (уже не единичной волны, а волны с периодом 2π) много больше, чем радиус a источника. Тогда, если нас интересуют волны вблизи от источника, мы можем считать, что за то время, когда волны проходят расстояние порядка нескольких десятков радиусов источника, величина pₐ практически не меняется: pₐ ≈ const. Пусть, далее, pₐ > 0, то есть сила, действующая на частицы среды, направлена от источника.
Еще раз посмотрим на эту картинку:

Согласно нашему предположению о совпадении фронтов волн с эквипотенциальными поверхностями, эти сферы – поверхности равного давления. Сила, как градиент давления, направлена по нормали к поверхности этих сфер. Проведем непрерывные силовые линии от источника таким образом, чтобы они были перпендикулярны всем этим сферам. Легко видеть, что силовые линии должны быть кривыми, причем загнутыми вперед, по направлению движения источника:

Если вы смотрите на эти силовые линии из СО покоящейся среды, в этом нет ничего удивительного, ведь это относится к последовательным единичным волнам, излученным из разных точек. Но напомню, что в СО источника так выглядят не только силовые линии, перпендикулярные фронтам последовательных единичных волн, но и силовые линии, перпендикулярные фронту одной и той же единичной волны в разные моменты времени. Обратите внимание, как сгущаются силовые линии перед источником: через единицу поверхности перед источником проходит намного больше силовых линий, чем сзади от него. Никакой симметрии «перед-зад» здесь и в помине нет.
Отредактировано: Yuri Rus - 02 дек 2019 03:31:43

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Чему равна сила звукового давления ΔF, действующая на элемент объема? Напомню, мы рассматриваем упрощенный вариант, где величина pₐ практически не меняется: pₐ ≈ const.
Вначале рассмотрим, чему равна сила звукового давления, создаваемая покоящимся источником. Волны давления разбегаются от источника, но поскольку мы считаем, что pₐ ≈ const, то на смену одной волне тут же приходит другая, с тем же самым значением давления в этой точке. Соответственно, сила давления в этой точке тоже будет примерно константой. Поэтому, мы можем убрать индексы 1, 2, 3… единичных волн, а писать просто p₀ и ΔF₀ (0 обозначает СО покоящейся среды); они не зависят от времени. Эта ситуация аналогична электростатике в классической физике, потому она для нас особо интересна. Можно сказать, что классическая электростатика описывает источник с бесконечной длиной волны (в квантовой механике появляются длины волн Де Бройля и Комптона).
Очевидно, сила ΔF₀ должна быть обратно пропорциональна квадрату расстояния r от источника, так же, как сила гравитации и Кулоновская сила. Величина же звукового давления p₀ обратно пропорциональна расстоянию от источника:
p₀ = pₐa / r = pₐa / (ct)
ΔF₀ = – ∇p ΔxΔyΔz = (pₐa r / r³) ΔxΔyΔz = (pₐa c / (c³t²)) ΔxΔyΔz
Допустим, на оси х давление в точках (x, 0, 0) и (x – Δx, 0, 0) равно
p₀(x, 0, 0) = pₐa/x
p₀(x – Δx, 0, 0) = pₐa/(x – Δx)
Δp₀/Δx = (p₀(x, 0, 0) – p₀(x – Δx, 0, 0))/Δx =
= (1 – 1/(1 – Δx/x)) pₐa/(x Δx) ≈ (1 – (1 + Δx/x)) pₐa/(x Δx) = – pₐa/x²
Рассмотрим теперь источник, движущийся по оси х со скоростью v. Обозначим β = v/c. Пусть в момент времени t=0 источник находился в начале координат и излучил первую единичную волну, которая за время t₁ распространилась во все стороны на расстояние r₁’(t₁) = ct₁ (в СО покоящейся среды) и образовала сферическую поверхность, во всех точках которой звуковое давление одинаково и равно
p₁(t₁) = pₐa / r₁’(t₁) = pₐa / (ct₁)
Штрих у r₁’ введен для единообразия обозначений с книгой Фейнмана, чтобы легче было сравнивать.
Чему будет равна сила, создаваемая звуковым давлением в точке Q₁(x₁, y₁, z₁) на этой сфере? Пусть угол между направлением движения источника и направлением от источника к точке Q₁ в момент излучения равен α₁. Казалось бы, можно просто воспользоваться формулой
ΔF₁ = – ∇p₁ ΔxΔyΔz = (pₐa r₁'/r₁’³) ΔxΔyΔz
Но это не так – дело в том, что выражение для p₁ относится только к одной единичной волне, распространение которой удовлетворяет уравнению
r₁'(t) = ct = i x(t) + j y(t) + k z(t)
Как я детально объяснял ранее, точки (x, y, z) и (x – dx, y, z) относятся либо к разным моментам времени у одной единичной волны, либо к разным единичным волнам в один момент времени. Градиент же давления, по определению, мы должны искать в один и тот же момент времени, но в разных точках пространства. Следовательно, чтобы найти градиент давления в точке Q₁ в определенный момент времени, мы должны использовать не одну, а, как минимум, две разных единичных волны.
В момент времени dt источник излучает вторую единичную волну:
r₂’(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
За время dt, источник сместился на расстояние v dt по оси х от начала координат. Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке Q₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки Q₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию вектора v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – β cos α₁)
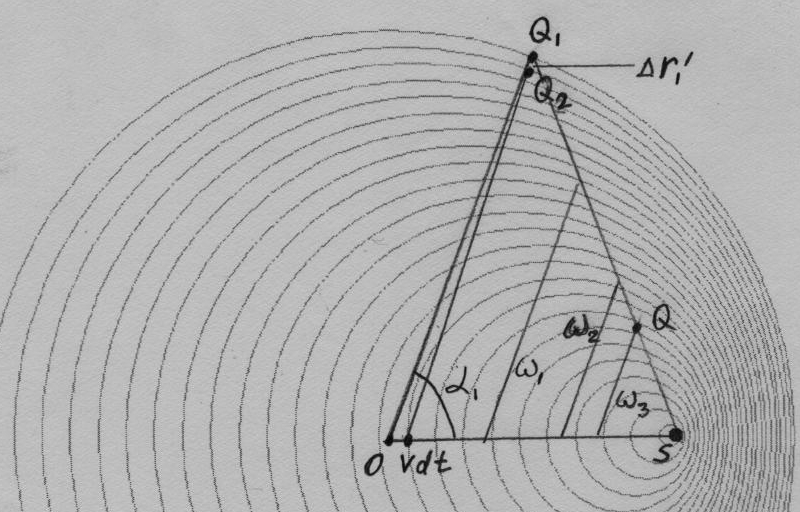
При этом, давление во всех точках сферы, образованной второй единичной волной, в момент t₁ равно
p₂(t₁) = pₐa / |r₂’(t₁) – v dt| = pₐa / (c (t₁ – dt))
Вектор градиента давления должен быть параллелен нормали к эквипотенциальной поверхности (поверхности равного давления). Поскольку мы исходим из предположения, что фронт каждой волны совпадает с эквипотенциальной поверхностью, то градиент давления в каждой точке будет параллелен вектору r'. Это означает, что градиент давления можно найти, просто продифференцировав Δp по Δr’ в каждой точке (в один и тот же момент времени). Для точки Q₁(x₁, y₁, z₁) это будет:
Δp₁(x₁, y₁, z₁, t₁) / Δr₁’ = (p₁(t₁) – p₂(t₁)) / (c dt (1 – β cos α₁)) =
= – pₐa / (r₁’² (1 – β cos α₁)) = – pₐa / ((c t₁)² (1 – β cos α₁))
ΔF₁(x₁, y₁, z₁, t₁) = pₐa r₁' / (r₁’³ (1 – β cos α₁)) ΔxΔyΔz = pₐa c / (c³t₁² (1 – β cos α₁)) ΔxΔyΔz
Кстати:
1 / (1 – β cos α₁) ≡ 1 / (1 – r₁'∙v / (r₁’c))
То есть, как видите, множитель вида 1 / (1 – r'∙v / (r’c)) у нас все-таки появился. Но он появился не для давления (то есть потенциала), а для силы давления. Есть разница (об этом ниже).
Вектор r₁' и угол α₁ относятся к положению источника в запаздывающий, нулевой момент времени, тогда как давление p₁ и сила ΔF₁ определяются в момент времени t₁. За время t₁, пока волна проходила расстояние r₁’ до точки Q₁, источник сместился по оси х на расстояние vt₁ = βr₁’ от начала координат. Обозначим расстояние от источника S(vt₁, 0, 0) до точки Q₁ (x₁, y₁, z₁) как r₁:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
Далее обозначим
u₁ = x₁ – vt₁ = x₁ – βr₁’.
Давайте перепишем уравнения для p₁ и ΔF₁ в точке Q₁ относительно r₁, u₁, y₁, и z₁, вместо r₁’, x₁, y₁, и z₁, то есть относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Воспользуемся уравнением:
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁² ,
Раскрыв скобки и перенеся все налево, мы можем выразить r₁' через u₁, y₁, z₁ и β путем решения квадратного уравнения
(1 – β²) r₁’² – 2 β u₁ r₁’ – (u₁² + y₁² + z₁²) = 0
Получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
Давление в точке Q₁ тогда равно:
p₁ = pₐa/r₁’ = pₐa (1 – β²) / (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)
Так же мы можем выразить ΔF₁ (в скалярной форме) через u₁, y₁, z₁ и β:
cos α₁ = x₁ / r₁'
А поскольку x₁ = u₁ + βr₁’ , то
cos α₁ = β + u₁ / r₁’
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
ΔF₁ = pₐa / (r₁’² (1 – β cos α₁)) ΔxΔyΔz =
= pₐa / ((β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
В векторной форме, ΔF₁ нужно умножить на единичный вектор в направлении r₁':
ΔF₁ = ΔF₁ r₁'/r₁' = ΔF (r₁ + vt₁) / |r₁ + vt₁| = pₐa (r₁ + vt₁) / (|r₁ + vt₁| (β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
Получилось довольно громоздкое выражение. Однако, все эти x₁, y₁, z₁, u₁, t₁ – не переменные, а фиксированные значения. Они относятся только к одной единичной волне, к одному моменту времени и к трем точкам (начало координат О, положение источника в момент t₁ и точка Q₁). Как будут выглядеть уравнения для p и ΔF для разных моментов времени, где x, y, z, u, t – это переменные, а не фиксированные значения?
Проведем прямую линию от положения источника в момент времени t₁ (точка S) к точке Q₁ (первая единичная волна из начала координат достигает ее также в момент t₁). Попробуем определить, чему равны давление p и сила ΔF в момент t₁ в других точках прямой SQ₁. Введем переменные при помощи переменного коэффициента ω:
u = ω u₁
Из вышеприведенного рисунка (где нарисованы первая и вторая единичные волны, точки О, S, Q₁ и Q₂) видно, что тогда остальные переменные, относящиеся к этой прямой и к моменту t₁, тоже можно выразить через ω (ω₁, ω₂, ω₃ – разные значения):
y = ω y₁ z = ω z₁ r = ω r₁
Давление в произвольной точке Q(u, y, z) будет равно
p = p₁ / ω = pₐa (1 – β²) / (ω (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)) =
= pₐa (1 – β²) / (ω (β u/ω + ((u/ω)² + (1 – β²) ((y/ω)² + (z/ω)²))½)) =
= pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
Аналогично, для силы мы получим
ΔF = pₐa / ((β u / (1 – β²)½ + (u² / (1 – β²) + y² + z²)½) (u² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Очень хорошо, мы избавились от ω и оказалось, что для переменных x, y, z, u это уравнение выглядит точно так же, как и для фиксированных значений x₁, y₁, z₁, u₁. А поскольку угол α₁ в первоначальном уравнении мог быть произвольным и он определялся соотношением между x₁ и r₁’, то уравнения для p и ΔF справедливы не только для прямой SQ₁, но во всем пространстве. Заметим, что время t₁ или t в этих уравнениях вообще не фигурирует, потому что они записаны для системы отсчета источника, и здесь на место одной единичной волны сразу же приходит другая, с теми же значениями p и ΔF (см. выше об источнике в СО покоящейся среды и аналогии с электростатикой).
Однако время, безусловно, должно фигурировать в уравнениях для СО покоящейся среды. Давайте совершим обратный переход в эту СО. Заменим
u = x – vt
где vt – это положение источника в момент t.
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½) =
= pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
ΔF = pₐa / ((β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
ΔF = pₐa (r + vt) / (|r + vt| (β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Читатель, конечно, уже обратил внимание, что здесь «напрашивается» та же самая замена, что и в преобразовани Лоренца для координаты:
x' = (x – vt)/(1 – β²)½ = γ (x – vt)
Да, уравнения для p и ΔF при этом немного упростятся:
p = pₐa / (γ (β x' + (x'² + y² + z²)½)
ΔF = pₐa / ((β x' + (x'² + y² + z²)½) (x'² + y² + z²)½) ΔxΔyΔz
Ну и что? Что это нам дает? Абсолютно ничего. А вот на что следует обратить особое внимание, это на то, что уравнения в СО покоящейся среды и в СО источника выглядят совершенно одинаково по форме и переход между ними осуществляется согласно преобразованию Галилея:
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
↓
p = pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
Уравнения для ΔF в разных системах отсчета выглядят тоже одинаково. В уравнениях в обеих СО, есть и (1 – β²), и β, и корень квадратный – в одинаковых местах. Более того, для вывода этих уравнений нам понадобилось перейти из СО покоящейся среды в СО источника при помощи преобразования Галилея, а потом обратно.
Между прочим, обратите внимание, что эти уравнения вовсе не описывают распространение сферических волн со скоростью c. Они описывают эквипотенциальные поверхности, которые, хотя и совпадают с мгновенным снимком фронтов волн, в отличие от последних, «заморожены» относительно источника. В СО источника, эквипотенциальные поверхности неподвижны. В СО покоящейся среды, они двигаются вместе с источником, с той же скоростью v. Как я уже говорил, это происходит потому, что на место одной единичной волны с определенными значениями p и ΔF тут же приходит другая волна, с теми же значениями. Это не статика в том смысле, что никакого движения нет; это динамическое равновесие.
Что касается фронтов волн, то они двигаются и в СО источника. Выведем формулу их распространения.
В СО покоящейся среды, фронты волн распространяются по формуле:
(x – ξ)² + y² + z² = c²(t – ԏ)²
где ξ – координата источника по оси x в момент времени ԏ, когда была излучена соответствующая единичная волна. Если источник движется с постоянной скоростью v, то ξ = vԏ.
При переходе в СО источника, мы должны воспользоваться преобразованием Галилея
u = x – vt или x = u + vt
Получим
(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²
Чтобы смысл этого уравнения был более понятен, запишем его немного по-другому, через единичные волны. Пусть первая единичная волна была излучена в момент dt (а не в нулевой, как я раньше писал; сейчас я меняю нумерацию ради получения более простого уравнения, чтобы там не было i -1), вторая – в момент 2 dt, третья – в момент 3 dt, а i-ая – в момент i dt. Тогда уравнение распространения i-ой волны можно записать как
(x – v i dt)² + y² + z² = c² (t – i dt)²
где ԏ = i dt, ξ(ԏ) = v i dt.
Перейдем в СО источника, произведя замену x = u + v t:
(u + v (t – i dt))² + y² + z² = c² (t – i dt)²
Это уравнение, действительно, описывает те самые сферические единичные волны, распространяющиеся со скоростью c и «сдуваемые» встречным ветром со скоростью –v. Так что описание волн давления в обеих СО выглядит полностью аналогичным. Галилей рулит.
Напомню еще раз, что всё это относится к упрощенному случаю очень большой длины волны, где мы можем считать, что давление на поверхности источника pₐ ≈ const, причем pₐ > 0. Пара слов о случае, когда pₐ < 0 и при этом pₐ ≈ const. Здесь просто зеркальное отражение случая pₐ > 0. Вся разница в том, что силовые линии направлены не от источника, а к источнику. Все остальное то же самое – силовые линии искривляются точно так же, все формулы просто меняют знаки плюс на минус и наоборот.
В случае переменного давления, когда pₐ более не константа и постоянно меняет знак, формулы для звукового давления p и силы ΔF более выполняться не будут, они будут иметь более сложный характер. На каком-то участке волны сила ΔF будет направлена от источника, на другом участке – к источнику (точнее, к той точке, где был источник в момент излучения данной единичной волны).
Но что важно: силовые линии останутся теми же самыми, искривленными точно так же (хотя на каждой силовой линии ΔF будет многократно менять знак и величину). Потому что фронты волн давления, совпадающие с эквипотенциальными поверхностями, будут распространяться точно так же, а сила перпендикулярна эквипотенциальным поверхностям.
Вначале рассмотрим, чему равна сила звукового давления, создаваемая покоящимся источником. Волны давления разбегаются от источника, но поскольку мы считаем, что pₐ ≈ const, то на смену одной волне тут же приходит другая, с тем же самым значением давления в этой точке. Соответственно, сила давления в этой точке тоже будет примерно константой. Поэтому, мы можем убрать индексы 1, 2, 3… единичных волн, а писать просто p₀ и ΔF₀ (0 обозначает СО покоящейся среды); они не зависят от времени. Эта ситуация аналогична электростатике в классической физике, потому она для нас особо интересна. Можно сказать, что классическая электростатика описывает источник с бесконечной длиной волны (в квантовой механике появляются длины волн Де Бройля и Комптона).
Очевидно, сила ΔF₀ должна быть обратно пропорциональна квадрату расстояния r от источника, так же, как сила гравитации и Кулоновская сила. Величина же звукового давления p₀ обратно пропорциональна расстоянию от источника:
p₀ = pₐa / r = pₐa / (ct)
ΔF₀ = – ∇p ΔxΔyΔz = (pₐa r / r³) ΔxΔyΔz = (pₐa c / (c³t²)) ΔxΔyΔz
Допустим, на оси х давление в точках (x, 0, 0) и (x – Δx, 0, 0) равно
p₀(x, 0, 0) = pₐa/x
p₀(x – Δx, 0, 0) = pₐa/(x – Δx)
Δp₀/Δx = (p₀(x, 0, 0) – p₀(x – Δx, 0, 0))/Δx =
= (1 – 1/(1 – Δx/x)) pₐa/(x Δx) ≈ (1 – (1 + Δx/x)) pₐa/(x Δx) = – pₐa/x²
Рассмотрим теперь источник, движущийся по оси х со скоростью v. Обозначим β = v/c. Пусть в момент времени t=0 источник находился в начале координат и излучил первую единичную волну, которая за время t₁ распространилась во все стороны на расстояние r₁’(t₁) = ct₁ (в СО покоящейся среды) и образовала сферическую поверхность, во всех точках которой звуковое давление одинаково и равно
p₁(t₁) = pₐa / r₁’(t₁) = pₐa / (ct₁)
Штрих у r₁’ введен для единообразия обозначений с книгой Фейнмана, чтобы легче было сравнивать.
Чему будет равна сила, создаваемая звуковым давлением в точке Q₁(x₁, y₁, z₁) на этой сфере? Пусть угол между направлением движения источника и направлением от источника к точке Q₁ в момент излучения равен α₁. Казалось бы, можно просто воспользоваться формулой
ΔF₁ = – ∇p₁ ΔxΔyΔz = (pₐa r₁'/r₁’³) ΔxΔyΔz
Но это не так – дело в том, что выражение для p₁ относится только к одной единичной волне, распространение которой удовлетворяет уравнению
r₁'(t) = ct = i x(t) + j y(t) + k z(t)
Как я детально объяснял ранее, точки (x, y, z) и (x – dx, y, z) относятся либо к разным моментам времени у одной единичной волны, либо к разным единичным волнам в один момент времени. Градиент же давления, по определению, мы должны искать в один и тот же момент времени, но в разных точках пространства. Следовательно, чтобы найти градиент давления в точке Q₁ в определенный момент времени, мы должны использовать не одну, а, как минимум, две разных единичных волны.
В момент времени dt источник излучает вторую единичную волну:
r₂’(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
За время dt, источник сместился на расстояние v dt по оси х от начала координат. Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке Q₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки Q₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию вектора v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – β cos α₁)

При этом, давление во всех точках сферы, образованной второй единичной волной, в момент t₁ равно
p₂(t₁) = pₐa / |r₂’(t₁) – v dt| = pₐa / (c (t₁ – dt))
Вектор градиента давления должен быть параллелен нормали к эквипотенциальной поверхности (поверхности равного давления). Поскольку мы исходим из предположения, что фронт каждой волны совпадает с эквипотенциальной поверхностью, то градиент давления в каждой точке будет параллелен вектору r'. Это означает, что градиент давления можно найти, просто продифференцировав Δp по Δr’ в каждой точке (в один и тот же момент времени). Для точки Q₁(x₁, y₁, z₁) это будет:
Δp₁(x₁, y₁, z₁, t₁) / Δr₁’ = (p₁(t₁) – p₂(t₁)) / (c dt (1 – β cos α₁)) =
= – pₐa / (r₁’² (1 – β cos α₁)) = – pₐa / ((c t₁)² (1 – β cos α₁))
ΔF₁(x₁, y₁, z₁, t₁) = pₐa r₁' / (r₁’³ (1 – β cos α₁)) ΔxΔyΔz = pₐa c / (c³t₁² (1 – β cos α₁)) ΔxΔyΔz
Кстати:
1 / (1 – β cos α₁) ≡ 1 / (1 – r₁'∙v / (r₁’c))
То есть, как видите, множитель вида 1 / (1 – r'∙v / (r’c)) у нас все-таки появился. Но он появился не для давления (то есть потенциала), а для силы давления. Есть разница (об этом ниже).
Вектор r₁' и угол α₁ относятся к положению источника в запаздывающий, нулевой момент времени, тогда как давление p₁ и сила ΔF₁ определяются в момент времени t₁. За время t₁, пока волна проходила расстояние r₁’ до точки Q₁, источник сместился по оси х на расстояние vt₁ = βr₁’ от начала координат. Обозначим расстояние от источника S(vt₁, 0, 0) до точки Q₁ (x₁, y₁, z₁) как r₁:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
Далее обозначим
u₁ = x₁ – vt₁ = x₁ – βr₁’.
Давайте перепишем уравнения для p₁ и ΔF₁ в точке Q₁ относительно r₁, u₁, y₁, и z₁, вместо r₁’, x₁, y₁, и z₁, то есть относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Воспользуемся уравнением:
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁² ,
Раскрыв скобки и перенеся все налево, мы можем выразить r₁' через u₁, y₁, z₁ и β путем решения квадратного уравнения
(1 – β²) r₁’² – 2 β u₁ r₁’ – (u₁² + y₁² + z₁²) = 0
Получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
Давление в точке Q₁ тогда равно:
p₁ = pₐa/r₁’ = pₐa (1 – β²) / (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)
Так же мы можем выразить ΔF₁ (в скалярной форме) через u₁, y₁, z₁ и β:
cos α₁ = x₁ / r₁'
А поскольку x₁ = u₁ + βr₁’ , то
cos α₁ = β + u₁ / r₁’
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
ΔF₁ = pₐa / (r₁’² (1 – β cos α₁)) ΔxΔyΔz =
= pₐa / ((β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
В векторной форме, ΔF₁ нужно умножить на единичный вектор в направлении r₁':
ΔF₁ = ΔF₁ r₁'/r₁' = ΔF (r₁ + vt₁) / |r₁ + vt₁| = pₐa (r₁ + vt₁) / (|r₁ + vt₁| (β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
Получилось довольно громоздкое выражение. Однако, все эти x₁, y₁, z₁, u₁, t₁ – не переменные, а фиксированные значения. Они относятся только к одной единичной волне, к одному моменту времени и к трем точкам (начало координат О, положение источника в момент t₁ и точка Q₁). Как будут выглядеть уравнения для p и ΔF для разных моментов времени, где x, y, z, u, t – это переменные, а не фиксированные значения?
Проведем прямую линию от положения источника в момент времени t₁ (точка S) к точке Q₁ (первая единичная волна из начала координат достигает ее также в момент t₁). Попробуем определить, чему равны давление p и сила ΔF в момент t₁ в других точках прямой SQ₁. Введем переменные при помощи переменного коэффициента ω:
u = ω u₁
Из вышеприведенного рисунка (где нарисованы первая и вторая единичные волны, точки О, S, Q₁ и Q₂) видно, что тогда остальные переменные, относящиеся к этой прямой и к моменту t₁, тоже можно выразить через ω (ω₁, ω₂, ω₃ – разные значения):
y = ω y₁ z = ω z₁ r = ω r₁
Давление в произвольной точке Q(u, y, z) будет равно
p = p₁ / ω = pₐa (1 – β²) / (ω (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)) =
= pₐa (1 – β²) / (ω (β u/ω + ((u/ω)² + (1 – β²) ((y/ω)² + (z/ω)²))½)) =
= pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
Аналогично, для силы мы получим
ΔF = pₐa / ((β u / (1 – β²)½ + (u² / (1 – β²) + y² + z²)½) (u² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Очень хорошо, мы избавились от ω и оказалось, что для переменных x, y, z, u это уравнение выглядит точно так же, как и для фиксированных значений x₁, y₁, z₁, u₁. А поскольку угол α₁ в первоначальном уравнении мог быть произвольным и он определялся соотношением между x₁ и r₁’, то уравнения для p и ΔF справедливы не только для прямой SQ₁, но во всем пространстве. Заметим, что время t₁ или t в этих уравнениях вообще не фигурирует, потому что они записаны для системы отсчета источника, и здесь на место одной единичной волны сразу же приходит другая, с теми же значениями p и ΔF (см. выше об источнике в СО покоящейся среды и аналогии с электростатикой).
Однако время, безусловно, должно фигурировать в уравнениях для СО покоящейся среды. Давайте совершим обратный переход в эту СО. Заменим
u = x – vt
где vt – это положение источника в момент t.
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½) =
= pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
ΔF = pₐa / ((β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
ΔF = pₐa (r + vt) / (|r + vt| (β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Читатель, конечно, уже обратил внимание, что здесь «напрашивается» та же самая замена, что и в преобразовани Лоренца для координаты:
x' = (x – vt)/(1 – β²)½ = γ (x – vt)
Да, уравнения для p и ΔF при этом немного упростятся:
p = pₐa / (γ (β x' + (x'² + y² + z²)½)
ΔF = pₐa / ((β x' + (x'² + y² + z²)½) (x'² + y² + z²)½) ΔxΔyΔz
Ну и что? Что это нам дает? Абсолютно ничего. А вот на что следует обратить особое внимание, это на то, что уравнения в СО покоящейся среды и в СО источника выглядят совершенно одинаково по форме и переход между ними осуществляется согласно преобразованию Галилея:
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
↓
p = pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
Уравнения для ΔF в разных системах отсчета выглядят тоже одинаково. В уравнениях в обеих СО, есть и (1 – β²), и β, и корень квадратный – в одинаковых местах. Более того, для вывода этих уравнений нам понадобилось перейти из СО покоящейся среды в СО источника при помощи преобразования Галилея, а потом обратно.
Между прочим, обратите внимание, что эти уравнения вовсе не описывают распространение сферических волн со скоростью c. Они описывают эквипотенциальные поверхности, которые, хотя и совпадают с мгновенным снимком фронтов волн, в отличие от последних, «заморожены» относительно источника. В СО источника, эквипотенциальные поверхности неподвижны. В СО покоящейся среды, они двигаются вместе с источником, с той же скоростью v. Как я уже говорил, это происходит потому, что на место одной единичной волны с определенными значениями p и ΔF тут же приходит другая волна, с теми же значениями. Это не статика в том смысле, что никакого движения нет; это динамическое равновесие.
Что касается фронтов волн, то они двигаются и в СО источника. Выведем формулу их распространения.
В СО покоящейся среды, фронты волн распространяются по формуле:
(x – ξ)² + y² + z² = c²(t – ԏ)²
где ξ – координата источника по оси x в момент времени ԏ, когда была излучена соответствующая единичная волна. Если источник движется с постоянной скоростью v, то ξ = vԏ.
При переходе в СО источника, мы должны воспользоваться преобразованием Галилея
u = x – vt или x = u + vt
Получим
(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²
Чтобы смысл этого уравнения был более понятен, запишем его немного по-другому, через единичные волны. Пусть первая единичная волна была излучена в момент dt (а не в нулевой, как я раньше писал; сейчас я меняю нумерацию ради получения более простого уравнения, чтобы там не было i -1), вторая – в момент 2 dt, третья – в момент 3 dt, а i-ая – в момент i dt. Тогда уравнение распространения i-ой волны можно записать как
(x – v i dt)² + y² + z² = c² (t – i dt)²
где ԏ = i dt, ξ(ԏ) = v i dt.
Перейдем в СО источника, произведя замену x = u + v t:
(u + v (t – i dt))² + y² + z² = c² (t – i dt)²
Это уравнение, действительно, описывает те самые сферические единичные волны, распространяющиеся со скоростью c и «сдуваемые» встречным ветром со скоростью –v. Так что описание волн давления в обеих СО выглядит полностью аналогичным. Галилей рулит.
Напомню еще раз, что всё это относится к упрощенному случаю очень большой длины волны, где мы можем считать, что давление на поверхности источника pₐ ≈ const, причем pₐ > 0. Пара слов о случае, когда pₐ < 0 и при этом pₐ ≈ const. Здесь просто зеркальное отражение случая pₐ > 0. Вся разница в том, что силовые линии направлены не от источника, а к источнику. Все остальное то же самое – силовые линии искривляются точно так же, все формулы просто меняют знаки плюс на минус и наоборот.
В случае переменного давления, когда pₐ более не константа и постоянно меняет знак, формулы для звукового давления p и силы ΔF более выполняться не будут, они будут иметь более сложный характер. На каком-то участке волны сила ΔF будет направлена от источника, на другом участке – к источнику (точнее, к той точке, где был источник в момент излучения данной единичной волны).
Но что важно: силовые линии останутся теми же самыми, искривленными точно так же (хотя на каждой силовой линии ΔF будет многократно менять знак и величину). Потому что фронты волн давления, совпадающие с эквипотенциальными поверхностями, будут распространяться точно так же, а сила перпендикулярна эквипотенциальным поверхностям.
Отредактировано: Yuri Rus - 02 дек 2019 03:33:35

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Давайте посмотрим, как Фейнман выводит первое преобразование Лоренца, также известное как сокращение длины Фитцджеральда-Лоренца.
Фейнман Р., Лейтон Р., Сэндс М. «Фейнмановские Лекции по Физике», т. 6 «Электродинамика», гл. 21, § 5-6, стр. 156-163:


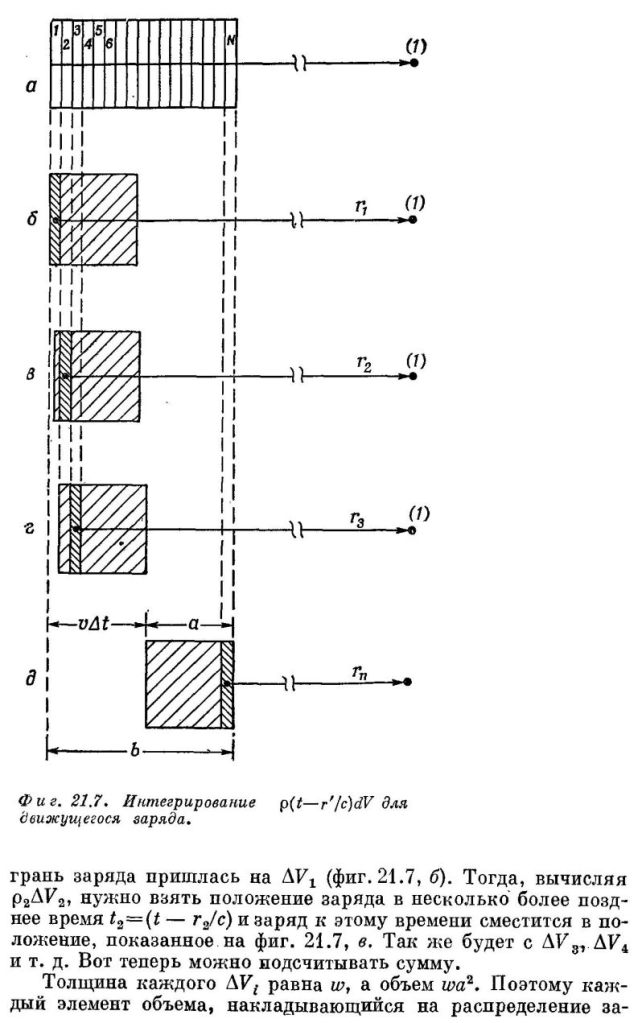





Здесь в формуле (21.39) опечатка – отсутствует знак корня у второго выражения (1 – β²). Вот эта формула из английского издания:
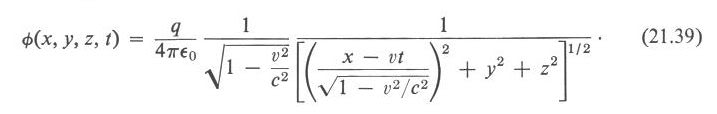
Пойдем по порядку. Уравнения (21.33) и (21.34), запаздывающие потенциалы Лиенара-Вихерта, по сравнению с используемым мной выше уравнением для звукового давления, содержат дополнительный множитель, такой же, как в эффекте Доплера (назовем его ЛВД множителем, Лиенара-Вихерта-Доплера):
1 / (1 – r’∙v / (r’c)) ≡ 1 / (1 – β cos α)
Именно благодаря наличию ЛВД множителя у потенциала φ, вместо уравнения
φ(x, y, z, t) = q (1 – β²) / (4πε₀ (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½))
возникает уравнение (21.39).
Таким образом, уравнения Лиенара-Вихерта, можно сказать, ответственны за возникновение преобразований Лоренца и теории относительности (хотя, как я уже писал, они вытекают и из определения полного дифференциала, и вообще из самого мат. аппарата физики). Я пока не хочу анализировать вывод этих уравнений для запаздывающих потенциалов; я это сделаю несколько позже. Сейчас же, временно, примем, что эти уравнения правильные, ЛВД множитель должен присутствовать в уравнениях для потенциалов. Сразу же можно сказать, что тогда этот множитель должен присутствовать и в уравнении для звукового давления, генерируемого движущимся источником. В выводе уравнений Лиенара-Вихерта нет ничего, что привязывало бы их только к уравнениям Максвелла и к абсолютному пределу – скорости света. Особенно это очевидно, когда вывод делается при помощи функций Грина и дельта-функции Дирака.
Стоит отметить следующее. В предыдущем разделе, когда я выводил формулы для звукового давления и силы давления, я сначала получил формулы для фиксированных значениях координат и времени: для одной единичной волны, излученной в начальный момент времени из начала координат, которая оказалась в определенной точке в фиксированный момент времени. Потом я перешел в СО источника и пересчитал давление и силу для этой точки в координатах источника. Только потом я распространил эти результаты на переменные координаты и время, и из СО источника вернулся в СО покоящейся среды. Из этого анализа было очевидно, что в обеих системах отсчета уравнения выглядят одинаково, а переход между ними осуществляется при помощи преобразования Галилея. Два наблюдателя, один в СО покоящейся среды и другой в СО источника, будут видеть распространение волн абсолютно одинаково.
Фейнман же использовал другой, более короткий вывод уравнения для потенциала, оставаясь все время только в СО покоящейся среды. В самом конце он, глядя на полученную формулу, делает предположение, что в СО источника это уравнение должно выглядеть совершенно иначе – а именно, так, как выглядело бы уравнение покоящегося источника в покоящейся среде. Я говорю «Фейнман» – подразумеваю всех физиков. Не он первым получил это уравнение и в книге дана не его личная, а общепринятая в современной физике интерпретация этого уравнения (в конце XIX века, оно интерпретировалось с позиции теории эфира).
Если же мы повторим ту же стратегию вывода уравнений для φ в системах отсчета покоящейся среды и источника, как в предыдущем разделе было сделано для звукового давления, мы увидим, что в обеих системах отсчета эти уравнения выглядят одинаково, что переход между этими СО осуществляется при помощи преобразования Галилея и что наблюдатель в СО источника будет регистрировать «сдувание встречным ветром» излучаемых источником волн.
Итак, проделаем весь анализ заново. Вначале я буду следовать Фейнману и покажу, что означает его вывод для фиксированных значений (их фиксированность подчеркнута нижним индексом 1 или 2).
Обратим внимание, что в главе 6 у Фейнмана выбор нулевого момента времени произволен, так же как и выбор начала координат. Мы можем выбрать их любым удобным для нас способом – и самым удобным в данной ситуации является такой вариант, при котором t' = 0 и в этот нулевой момент времени заряд находится в начале координат. То есть отсчет времени логично начинать в тот момент, когда заряд излучает сферическую волну потенциала φ₁, которая в момент времени t₁ достигает точки P(x₁, y₁, z₁), тогда как заряд в момент t₁ оказывается в точке с координатами (vt₁, 0, 0). Это позволяет нам значительно упростить все рассуждения, нисколько не меняя их смысла, и формулы Фейнмана будут переписаны так:
t₁ = r₁’/c (21.35)’
r₁’ = (x₁² + y₁² + z₁²)½ (21.36)’
Следующие 2 уравнения, при t’ = 0, сводятся к
c²t₁² = x₁² + y₁² + z₁²
К этому же выражению сводится и уравнение
t₁ – vx₁/c² = ((x₁ – vt₁)² + (1 – β²) (y₁² + z₁²))½) / c (21.37)’
которое, после возведения левой и правой частей в квадрат, станет
c²t₁² (1 – β²) = x₁² (1 – β²) + (y₁² + z₁²) (1 – β²)
то есть опять же превратится в
c²t₁² = x₁² + y₁² + z₁²
Далее, r₁' = ct₁, а уравнение для потенциала φ₁ станет
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (r₁’ – r₁’∙v / c)) (21.38 )’
Составляющая v в направлении r₁' равна vx₁/r₁', так что v∙r₁' просто равно vx₁, а весь знаменатель равен
ct₁ – vx₁/c = c (t₁ – vx₁/c²)
Подставив это в уравнение (21.38 ), получим
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
То есть это всё то же уравнение для потенциала Лиенара-Вихерта (для фиксированной точки, фиксированного момента времени и одной единичной волны, излученной в нулевой момент времени), а не
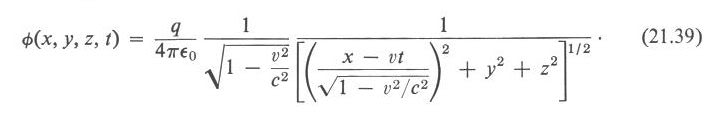
Теперь, чтобы получить уравнения для φ в системах отсчета покоящейся среды и источника при переменных координатах и времени, воспользуемся той же стратегией, как в предыдущем разделе было сделано для звукового давления.
Пусть в момент времени t = 0 заряд излучает первую сферическую единичную волну потенциала φ, которая распространяется по закону
r₁(t) = ct = i x(t) + j y(t) + k z(t)
или
x²(t) + y²(t) + z²(t) = c²t²
Будем полагать, что потенциал φ₁ в каждой точке этой единичной волны меняется по формуле Лиенара-Вихерта:
φ₁(x, y, z, t) = q / (4πε₀ ((x² + y² + z²)½ – vx/c)) = q / (4πε₀ (ct – vx/c))
В момент времени t₁, первая волна достигает точки P₁(x₁, y₁, z₁). Потенциал φ₁ в этой точке равен
φ₁(x₁, y₁, z₁, t₁) = q / (4πε₀ ((x₁² + y₁² + z₁²)½ – vx₁/c)) = q / (4πε₀ (ct₁ – vx₁/c))
Из-за ЛВД множителя, эквипотенциальные поверхности больше не совпадают с фронтами волн φ, поэтому вектор ∇φ более не параллелен вектору r’. Мы, конечно, можем определить направление градиента по частям, определив значения ∂φ/∂x, ∂φ/∂y, ∂φ/∂z, а потом еще добавить ∂Ax/∂t, ∂Ay/∂t, ∂Az/∂t. Именно так делал Фейнман в главе 26. Но мы пока этого делать не будем, это только даст много непринципиальной писанины. Возможно, потом.
Сейчас определим только, чему равна производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁, т.е. Δφ₁ / Δr₁’. Это будет нам более полезно.
За время dt, источник сместился из начала координат в точку (v dt, 0, 0). В момент времени dt, источник излучает вторую сферическую единичную волну φ, которая распространяется по закону
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Потенциал φ₂ в каждой точке второй единичной волны будет меняться по закону:
φ₂(x, y, z, t) = q / (4πε₀ (((x – v dt)² + y² + z²)½ – v(x – v dt)/c)) = q / (4πε₀ (c(t – dt) – v(x – v dt)/c))
Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке P₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки P₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию расстояния v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – r₁’∙v / (r₁’c)) ≡ c dt (1 – β cos α₁).
Потенциал φ₂ в этой точке равен
φ₂( x₂, y₂, z₂, t₁) = q / (4πε₀c (t₁ – dt) (1 – β cos α₁))
Итак, производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁ будет равна:
Δφ₁ / Δr₁’ = (φ₁(t₁) – φ₂(t₁)) / (c dt (1 – β cos α₁)) =
= – q / (4πε₀ (r₁’² (1 – β cos α₁)²)) = – q / (4πε₀ ((c t₁)² (1 – β cos α₁)²))
Мы видим, что Δφ₁ / Δr₁’ отличается от φ₁ появлением второго ЛВД множителя, то есть 1 / (1 – β cos α₁). В предыдущем разделе, когда мы предположили, что фронты волн и эквипотенциальные поверхности совпадают, Δp₁ / Δr₁’ отличалась от p₁ точно таким же ЛВД множителем. Этот же множитель появляется и для частоты звуковой волны, если источник движется. Везде – по той же самой причине. Для простоты, примем, что наблюдатель (детектор) находится на оси х. Спереди от источника, фронты волн будут расположены в 1/(1 – β) раз чаще, а сзади – в 1/(1 + β) раз реже, чем у покоящегося источника. Но эти фронты волн соответствуют разным значениям φ или p. Чем чаще расположены фронты последовательных волн, тем круче падение кривой φ или p, тем больше значение соответствующей производной.
Любая переменная f, для которой можно записать волновое уравнение вида
∂²f/∂t² – c²∇²f = S(x – ξ, y, z, t – ԏ)
имеет фронты волн, распространяющиеся со скоростью c. Производная f по r’ всегда будет приобретать ЛВД множитель, каков бы ни был вид зависимости самой f от r’.
Теперь перейдем в СО источника, используя преобразование Галилея для координат:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
u₁ = x₁ – vt₁ = x₁ – βr₁’
и перепишем уравнение для φ₁ в точке P₁ относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Полностью аналогично тому, как это было сделано выше для звукового давления, из уравнения
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁²
раскрыв скобки в (u₁ + βr₁’)² и перенеся все налево, путем решения квадратного уравнения относительно степеней r₁', мы получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
Тогда φ₁ в СО источника равен:
φ₁(u₁, y₁, z₁) = q / (4πε₀ (u₁² + (1 – β²) (y₁² + z₁²))½)
Остановимся на секунду. До сих пор все эти рассуждения и уравнения относились только к фиксированным значениям (одна единичная волна, излученная в нулевой момент времени и в другой момент достигающая определенной точки). Обратите внимание – только когда мы перешли в СО источника, воспользовавшись для этого преобразованием Галилея, а не Лоренца, мы получили уравнение, аналогичное уравнению (21.39) Фейнмана.
Тогда как раньше, напомню, для этих же фиксированных значений в СО покоящейся среды мы имели всего лишь уравнение для потенциала Лиенара-Вихерта:
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
Теперь перейдем от фиксированных значений x₁, y₁, z₁, u₁, t₁ к переменным x, y, z, u, t. Введем их при помощи переменного коэффициента ω:
u = ω u₁ y = ω y₁ z = ω z₁ r = ω r₁
Тогда φ в произвольной точке P(u, y, z) будет равен:
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
Теперь давайте совершим обратный переход в СО покоящейся среды. Заменим
u = x – vt
где vt – это положение источника в момент t.
φ(x, y, z, t) = q / (4πε₀ ((x – vt)² + (1 – β²) (y² + z²))½) ≡
≡ q / (4πε₀ (1 – β²)½ ((x – vt)² / (1 – β²) + y² + z²)½)
Это уравнение полностью совпадает с уравнением Фейнмана (21.39). Здесь Фейнман написал:

Однако, как мы видели, это не так: для вывода этих уравнений, мы из СО покоящейся среды перешли в СО источника, причем именно при помощи преобразования Галилея u = x – vt, затем обратно. И в обеих этих системах отсчета, уравнения для φ выглядят совершенно одинаково (единственная разница – замена u на x – vt). Потенциал φ в СО источника выглядит как
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
а вовсе не как
φ(u, y, z) = q / (4πε₀ (u² + y² + z²)½)
Это я и имел в виду, когда писал, что Фейнман дает формуле (21.39) совершенно неправильную интерпретацию, в частности, потому, что у него отсутствует переход из одной системы отсчета в другую при выводе этих уравнений.
Фейнман Р., Лейтон Р., Сэндс М. «Фейнмановские Лекции по Физике», т. 6 «Электродинамика», гл. 21, § 5-6, стр. 156-163:








Здесь в формуле (21.39) опечатка – отсутствует знак корня у второго выражения (1 – β²). Вот эта формула из английского издания:
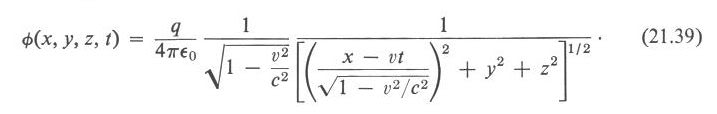
Пойдем по порядку. Уравнения (21.33) и (21.34), запаздывающие потенциалы Лиенара-Вихерта, по сравнению с используемым мной выше уравнением для звукового давления, содержат дополнительный множитель, такой же, как в эффекте Доплера (назовем его ЛВД множителем, Лиенара-Вихерта-Доплера):
1 / (1 – r’∙v / (r’c)) ≡ 1 / (1 – β cos α)
Именно благодаря наличию ЛВД множителя у потенциала φ, вместо уравнения
φ(x, y, z, t) = q (1 – β²) / (4πε₀ (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½))
возникает уравнение (21.39).
Таким образом, уравнения Лиенара-Вихерта, можно сказать, ответственны за возникновение преобразований Лоренца и теории относительности (хотя, как я уже писал, они вытекают и из определения полного дифференциала, и вообще из самого мат. аппарата физики). Я пока не хочу анализировать вывод этих уравнений для запаздывающих потенциалов; я это сделаю несколько позже. Сейчас же, временно, примем, что эти уравнения правильные, ЛВД множитель должен присутствовать в уравнениях для потенциалов. Сразу же можно сказать, что тогда этот множитель должен присутствовать и в уравнении для звукового давления, генерируемого движущимся источником. В выводе уравнений Лиенара-Вихерта нет ничего, что привязывало бы их только к уравнениям Максвелла и к абсолютному пределу – скорости света. Особенно это очевидно, когда вывод делается при помощи функций Грина и дельта-функции Дирака.
Стоит отметить следующее. В предыдущем разделе, когда я выводил формулы для звукового давления и силы давления, я сначала получил формулы для фиксированных значениях координат и времени: для одной единичной волны, излученной в начальный момент времени из начала координат, которая оказалась в определенной точке в фиксированный момент времени. Потом я перешел в СО источника и пересчитал давление и силу для этой точки в координатах источника. Только потом я распространил эти результаты на переменные координаты и время, и из СО источника вернулся в СО покоящейся среды. Из этого анализа было очевидно, что в обеих системах отсчета уравнения выглядят одинаково, а переход между ними осуществляется при помощи преобразования Галилея. Два наблюдателя, один в СО покоящейся среды и другой в СО источника, будут видеть распространение волн абсолютно одинаково.
Фейнман же использовал другой, более короткий вывод уравнения для потенциала, оставаясь все время только в СО покоящейся среды. В самом конце он, глядя на полученную формулу, делает предположение, что в СО источника это уравнение должно выглядеть совершенно иначе – а именно, так, как выглядело бы уравнение покоящегося источника в покоящейся среде. Я говорю «Фейнман» – подразумеваю всех физиков. Не он первым получил это уравнение и в книге дана не его личная, а общепринятая в современной физике интерпретация этого уравнения (в конце XIX века, оно интерпретировалось с позиции теории эфира).
Если же мы повторим ту же стратегию вывода уравнений для φ в системах отсчета покоящейся среды и источника, как в предыдущем разделе было сделано для звукового давления, мы увидим, что в обеих системах отсчета эти уравнения выглядят одинаково, что переход между этими СО осуществляется при помощи преобразования Галилея и что наблюдатель в СО источника будет регистрировать «сдувание встречным ветром» излучаемых источником волн.
Итак, проделаем весь анализ заново. Вначале я буду следовать Фейнману и покажу, что означает его вывод для фиксированных значений (их фиксированность подчеркнута нижним индексом 1 или 2).
Обратим внимание, что в главе 6 у Фейнмана выбор нулевого момента времени произволен, так же как и выбор начала координат. Мы можем выбрать их любым удобным для нас способом – и самым удобным в данной ситуации является такой вариант, при котором t' = 0 и в этот нулевой момент времени заряд находится в начале координат. То есть отсчет времени логично начинать в тот момент, когда заряд излучает сферическую волну потенциала φ₁, которая в момент времени t₁ достигает точки P(x₁, y₁, z₁), тогда как заряд в момент t₁ оказывается в точке с координатами (vt₁, 0, 0). Это позволяет нам значительно упростить все рассуждения, нисколько не меняя их смысла, и формулы Фейнмана будут переписаны так:
t₁ = r₁’/c (21.35)’
r₁’ = (x₁² + y₁² + z₁²)½ (21.36)’
Следующие 2 уравнения, при t’ = 0, сводятся к
c²t₁² = x₁² + y₁² + z₁²
К этому же выражению сводится и уравнение
t₁ – vx₁/c² = ((x₁ – vt₁)² + (1 – β²) (y₁² + z₁²))½) / c (21.37)’
которое, после возведения левой и правой частей в квадрат, станет
c²t₁² (1 – β²) = x₁² (1 – β²) + (y₁² + z₁²) (1 – β²)
то есть опять же превратится в
c²t₁² = x₁² + y₁² + z₁²
Далее, r₁' = ct₁, а уравнение для потенциала φ₁ станет
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (r₁’ – r₁’∙v / c)) (21.38 )’
Составляющая v в направлении r₁' равна vx₁/r₁', так что v∙r₁' просто равно vx₁, а весь знаменатель равен
ct₁ – vx₁/c = c (t₁ – vx₁/c²)
Подставив это в уравнение (21.38 ), получим
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
То есть это всё то же уравнение для потенциала Лиенара-Вихерта (для фиксированной точки, фиксированного момента времени и одной единичной волны, излученной в нулевой момент времени), а не
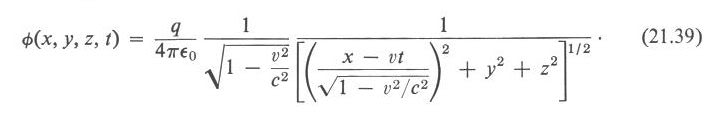
Теперь, чтобы получить уравнения для φ в системах отсчета покоящейся среды и источника при переменных координатах и времени, воспользуемся той же стратегией, как в предыдущем разделе было сделано для звукового давления.
Пусть в момент времени t = 0 заряд излучает первую сферическую единичную волну потенциала φ, которая распространяется по закону
r₁(t) = ct = i x(t) + j y(t) + k z(t)
или
x²(t) + y²(t) + z²(t) = c²t²
Будем полагать, что потенциал φ₁ в каждой точке этой единичной волны меняется по формуле Лиенара-Вихерта:
φ₁(x, y, z, t) = q / (4πε₀ ((x² + y² + z²)½ – vx/c)) = q / (4πε₀ (ct – vx/c))
В момент времени t₁, первая волна достигает точки P₁(x₁, y₁, z₁). Потенциал φ₁ в этой точке равен
φ₁(x₁, y₁, z₁, t₁) = q / (4πε₀ ((x₁² + y₁² + z₁²)½ – vx₁/c)) = q / (4πε₀ (ct₁ – vx₁/c))
Из-за ЛВД множителя, эквипотенциальные поверхности больше не совпадают с фронтами волн φ, поэтому вектор ∇φ более не параллелен вектору r’. Мы, конечно, можем определить направление градиента по частям, определив значения ∂φ/∂x, ∂φ/∂y, ∂φ/∂z, а потом еще добавить ∂Ax/∂t, ∂Ay/∂t, ∂Az/∂t. Именно так делал Фейнман в главе 26. Но мы пока этого делать не будем, это только даст много непринципиальной писанины. Возможно, потом.
Сейчас определим только, чему равна производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁, т.е. Δφ₁ / Δr₁’. Это будет нам более полезно.
За время dt, источник сместился из начала координат в точку (v dt, 0, 0). В момент времени dt, источник излучает вторую сферическую единичную волну φ, которая распространяется по закону
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Потенциал φ₂ в каждой точке второй единичной волны будет меняться по закону:
φ₂(x, y, z, t) = q / (4πε₀ (((x – v dt)² + y² + z²)½ – v(x – v dt)/c)) = q / (4πε₀ (c(t – dt) – v(x – v dt)/c))
Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке P₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки P₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию расстояния v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – r₁’∙v / (r₁’c)) ≡ c dt (1 – β cos α₁).
Потенциал φ₂ в этой точке равен
φ₂( x₂, y₂, z₂, t₁) = q / (4πε₀c (t₁ – dt) (1 – β cos α₁))
Итак, производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁ будет равна:
Δφ₁ / Δr₁’ = (φ₁(t₁) – φ₂(t₁)) / (c dt (1 – β cos α₁)) =
= – q / (4πε₀ (r₁’² (1 – β cos α₁)²)) = – q / (4πε₀ ((c t₁)² (1 – β cos α₁)²))
Мы видим, что Δφ₁ / Δr₁’ отличается от φ₁ появлением второго ЛВД множителя, то есть 1 / (1 – β cos α₁). В предыдущем разделе, когда мы предположили, что фронты волн и эквипотенциальные поверхности совпадают, Δp₁ / Δr₁’ отличалась от p₁ точно таким же ЛВД множителем. Этот же множитель появляется и для частоты звуковой волны, если источник движется. Везде – по той же самой причине. Для простоты, примем, что наблюдатель (детектор) находится на оси х. Спереди от источника, фронты волн будут расположены в 1/(1 – β) раз чаще, а сзади – в 1/(1 + β) раз реже, чем у покоящегося источника. Но эти фронты волн соответствуют разным значениям φ или p. Чем чаще расположены фронты последовательных волн, тем круче падение кривой φ или p, тем больше значение соответствующей производной.
Любая переменная f, для которой можно записать волновое уравнение вида
∂²f/∂t² – c²∇²f = S(x – ξ, y, z, t – ԏ)
имеет фронты волн, распространяющиеся со скоростью c. Производная f по r’ всегда будет приобретать ЛВД множитель, каков бы ни был вид зависимости самой f от r’.
Теперь перейдем в СО источника, используя преобразование Галилея для координат:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
u₁ = x₁ – vt₁ = x₁ – βr₁’
и перепишем уравнение для φ₁ в точке P₁ относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Полностью аналогично тому, как это было сделано выше для звукового давления, из уравнения
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁²
раскрыв скобки в (u₁ + βr₁’)² и перенеся все налево, путем решения квадратного уравнения относительно степеней r₁', мы получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
Тогда φ₁ в СО источника равен:
φ₁(u₁, y₁, z₁) = q / (4πε₀ (u₁² + (1 – β²) (y₁² + z₁²))½)
Остановимся на секунду. До сих пор все эти рассуждения и уравнения относились только к фиксированным значениям (одна единичная волна, излученная в нулевой момент времени и в другой момент достигающая определенной точки). Обратите внимание – только когда мы перешли в СО источника, воспользовавшись для этого преобразованием Галилея, а не Лоренца, мы получили уравнение, аналогичное уравнению (21.39) Фейнмана.
Тогда как раньше, напомню, для этих же фиксированных значений в СО покоящейся среды мы имели всего лишь уравнение для потенциала Лиенара-Вихерта:
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
Теперь перейдем от фиксированных значений x₁, y₁, z₁, u₁, t₁ к переменным x, y, z, u, t. Введем их при помощи переменного коэффициента ω:
u = ω u₁ y = ω y₁ z = ω z₁ r = ω r₁
Тогда φ в произвольной точке P(u, y, z) будет равен:
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
Теперь давайте совершим обратный переход в СО покоящейся среды. Заменим
u = x – vt
где vt – это положение источника в момент t.
φ(x, y, z, t) = q / (4πε₀ ((x – vt)² + (1 – β²) (y² + z²))½) ≡
≡ q / (4πε₀ (1 – β²)½ ((x – vt)² / (1 – β²) + y² + z²)½)
Это уравнение полностью совпадает с уравнением Фейнмана (21.39). Здесь Фейнман написал:

Однако, как мы видели, это не так: для вывода этих уравнений, мы из СО покоящейся среды перешли в СО источника, причем именно при помощи преобразования Галилея u = x – vt, затем обратно. И в обеих этих системах отсчета, уравнения для φ выглядят совершенно одинаково (единственная разница – замена u на x – vt). Потенциал φ в СО источника выглядит как
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
а вовсе не как
φ(u, y, z) = q / (4πε₀ (u² + y² + z²)½)
Это я и имел в виду, когда писал, что Фейнман дает формуле (21.39) совершенно неправильную интерпретацию, в частности, потому, что у него отсутствует переход из одной системы отсчета в другую при выводе этих уравнений.
Отредактировано: Yuri Rus - 25 фев 2020 17:59:59

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Но давайте дальше разберемся, что же означает уравнение (21.39), что именно у нас будет сплюснуто в γ раз. А сплюснутыми оказываются эквипотенциальные поверхности, которые «заморожены» относительно источника:
В то же время, сферические фронты волн φ по-прежнему распространяются со скоростью света во все стороны от тех точек, где находился источник в момент их излучения:
Подчеркну, что так выглядит картина распространения фронтов волн и эквипотенциальные поверхности в обеих системах отсчета (точнее, во всех инерциальных СО). В СО покоящейся среды, фронты волн распространяются по формуле:
(x – ξ)² + y² + z² = c²(t – ԏ)²
или, для i-ой единичной волны:
(x – v i dt)² + y² + z² = c² (t – i dt)²
При переходе в СО источника, воспользуемся преобразованием Галилея x = u + vt. Получим
(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²
или
(u + v (t – i dt))² + y² + z² = c² (t – i dt)²
Это уравнение описывает сферические фронты волн, распространяющиеся со скоростью c и «сдуваемые» встречным ветром со скоростью –v. Галилей по-прежнему рулит, хотя теперь эквипотенциальные поверхности больше не выглядят так же, как фронты волн (см. предыдущий раздел).
Как я уже говорил, вывод уравнения Лиенара-Вихерта не содержит в себе ничего специфического только для уравнений Максвелла, для скорости света. Если уравнение для запаздывающего потенциала φ действительно корректно, то оно должно относиться ко всем другим волнам. В частности, тогда уравнение для звукового давления тоже должно включать в себя ЛВД множитель:
p = pₐa / (r’ – r’∙v / c)) = pₐa / (r’ (1 – β cos α)).
При одном и том же значении r' (т.е. на поверхности сферы радиусом r' ), значения p будут отличаться – они будут максимальны спереди от движущегося источника и минимальны сзади от него. Давайте посмотрим, что произойдет, если мы будем постепенно уменьшать радиус r'. Очевидно, величина p будет возрастать обратно пропорционально уменьшению r', тогда как относительные значения p в разных местах сферы меньшего радиуса останутся такими же, как у сферы большего радиуса (в сферических координатах, зависимость p от углов θ и φ одинакова при любом r' ). Все более уменьшая r', в пределе мы дойдем до поверхности источника – сферы радиуса a. Прямо над этой поверхностью, давление pₐ тоже должно подчиняться зависимости
pₐ= pₐ₀ / (1 – β cos α)
где pₐ₀ – давление на поверхности источника (радиуса a), когда источник покоится относительно среды; оно одинаково во всех точках этой поверхности.
То есть pₐ(a, α) более не одинакова во всех точках поверхности источника, как мы постулировали вначале.
Но это означает, что в вышеприведенное уравнение для давления должно входить не pₐ, а pₐ₀:
p = pₐ₀a / (r’ – r’∙v / c)) = pₐ₀a / (r’ (1 – β cos α))
что эквивалентно
p = pₐ(a, α) a / r’
Давайте разберемся, что это означает. Во-первых, это означает, что при движении источника в разных точках его поверхности давление различается. Спереди от источника (угол α меньше 90°), давление становится больше в 1 / (1 – β cos α) раз, а сзади (угол α больше 90°) – меньше. Вообще говоря, эта идея кажется достаточно логичной: благодаря движению источника, спереди от него жидкость, действительно, может стать плотнее, а сзади – более разреженной, по сравнению с покоящимся источником. Во-вторых, это означает, что давление на расстоянии от источника определяется именно распределением давления на поверхности источника, оно передается во все стороны без искажений (в «нулевом приближении»). А это означает, что уравнение Лиенара-Вихерта неверно.
Как это? А вот так – при выводе этого уравнения утверждается, что ЛВД множитель возникает именно из-за запаздывания, из-за того, что интеграл как-то там проносится над зарядом и т.д. Если же этот множитель возникает из-за того, что давление в разных точках поверхности источника неодинаково и имеет следующую зависимость
pₐ= pₐ₀ / (1 – β cos α)
то запаздывание и процедура интегрирования в движении здесь совершенно ни при чем. Собственно говоря, если зависимость pₐ от, допустим, углов θ и φ, в сферических координатах, имеет другой характер, то и давление на расстоянии от источника будет иметь точно такой же характер. Потому что совсем не обязательно, чтобы pₐ имела непременно такую зависимость:
pₐ= pₐ₀ / (1 – β cos α)
Зависимость эту надо определять отдельно, из других физических соображений. Даже если, допустим, для сферы зависимость именно такая, то для источника с другой формой поверхности она будет подчиняться какому-то другому уравнению.
Аналогично, для движущегося сферического заряда радиуса a мы получим, что потенциал φ у самой его поверхности подчиняется уравнению
φₐ= φₐ₀ / (1 – β cos α)
где φₐ₀ – потенциал рядом с поверхностью заряда (на бесконечно малом расстоянии от нее), когда заряд покоится относительно среды.
Это, по-видимому, означает, что при движении заряда его поверхностная плотность не одинакова в разных точках или объемная плотность неодинакова во всем объеме заряда. Теоретически, это можно проверить, если исследовать движение заряженной сферы в вакууме и перераспределение зарядов на ее поверхности. Причем измерять надо не напряженность электрического поля вокруг заряда (потому что одни и те же изменения поля можно интерпретировать по-разному, как в рамках «классической» теории, так и в рамках моей теории), а само распределение зарядов (или токи) на поверхности сферы. Но при тех скоростях, которые достижимы в настоящее время, зарегистрировать такое перераспределение зарядов будет не так просто.

В то же время, сферические фронты волн φ по-прежнему распространяются со скоростью света во все стороны от тех точек, где находился источник в момент их излучения:

Подчеркну, что так выглядит картина распространения фронтов волн и эквипотенциальные поверхности в обеих системах отсчета (точнее, во всех инерциальных СО). В СО покоящейся среды, фронты волн распространяются по формуле:
(x – ξ)² + y² + z² = c²(t – ԏ)²
или, для i-ой единичной волны:
(x – v i dt)² + y² + z² = c² (t – i dt)²
При переходе в СО источника, воспользуемся преобразованием Галилея x = u + vt. Получим
(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²
или
(u + v (t – i dt))² + y² + z² = c² (t – i dt)²
Это уравнение описывает сферические фронты волн, распространяющиеся со скоростью c и «сдуваемые» встречным ветром со скоростью –v. Галилей по-прежнему рулит, хотя теперь эквипотенциальные поверхности больше не выглядят так же, как фронты волн (см. предыдущий раздел).
Как я уже говорил, вывод уравнения Лиенара-Вихерта не содержит в себе ничего специфического только для уравнений Максвелла, для скорости света. Если уравнение для запаздывающего потенциала φ действительно корректно, то оно должно относиться ко всем другим волнам. В частности, тогда уравнение для звукового давления тоже должно включать в себя ЛВД множитель:
p = pₐa / (r’ – r’∙v / c)) = pₐa / (r’ (1 – β cos α)).
При одном и том же значении r' (т.е. на поверхности сферы радиусом r' ), значения p будут отличаться – они будут максимальны спереди от движущегося источника и минимальны сзади от него. Давайте посмотрим, что произойдет, если мы будем постепенно уменьшать радиус r'. Очевидно, величина p будет возрастать обратно пропорционально уменьшению r', тогда как относительные значения p в разных местах сферы меньшего радиуса останутся такими же, как у сферы большего радиуса (в сферических координатах, зависимость p от углов θ и φ одинакова при любом r' ). Все более уменьшая r', в пределе мы дойдем до поверхности источника – сферы радиуса a. Прямо над этой поверхностью, давление pₐ тоже должно подчиняться зависимости
pₐ= pₐ₀ / (1 – β cos α)
где pₐ₀ – давление на поверхности источника (радиуса a), когда источник покоится относительно среды; оно одинаково во всех точках этой поверхности.
То есть pₐ(a, α) более не одинакова во всех точках поверхности источника, как мы постулировали вначале.
Но это означает, что в вышеприведенное уравнение для давления должно входить не pₐ, а pₐ₀:
p = pₐ₀a / (r’ – r’∙v / c)) = pₐ₀a / (r’ (1 – β cos α))
что эквивалентно
p = pₐ(a, α) a / r’
Давайте разберемся, что это означает. Во-первых, это означает, что при движении источника в разных точках его поверхности давление различается. Спереди от источника (угол α меньше 90°), давление становится больше в 1 / (1 – β cos α) раз, а сзади (угол α больше 90°) – меньше. Вообще говоря, эта идея кажется достаточно логичной: благодаря движению источника, спереди от него жидкость, действительно, может стать плотнее, а сзади – более разреженной, по сравнению с покоящимся источником. Во-вторых, это означает, что давление на расстоянии от источника определяется именно распределением давления на поверхности источника, оно передается во все стороны без искажений (в «нулевом приближении»). А это означает, что уравнение Лиенара-Вихерта неверно.
Как это? А вот так – при выводе этого уравнения утверждается, что ЛВД множитель возникает именно из-за запаздывания, из-за того, что интеграл как-то там проносится над зарядом и т.д. Если же этот множитель возникает из-за того, что давление в разных точках поверхности источника неодинаково и имеет следующую зависимость
pₐ= pₐ₀ / (1 – β cos α)
то запаздывание и процедура интегрирования в движении здесь совершенно ни при чем. Собственно говоря, если зависимость pₐ от, допустим, углов θ и φ, в сферических координатах, имеет другой характер, то и давление на расстоянии от источника будет иметь точно такой же характер. Потому что совсем не обязательно, чтобы pₐ имела непременно такую зависимость:
pₐ= pₐ₀ / (1 – β cos α)
Зависимость эту надо определять отдельно, из других физических соображений. Даже если, допустим, для сферы зависимость именно такая, то для источника с другой формой поверхности она будет подчиняться какому-то другому уравнению.
Аналогично, для движущегося сферического заряда радиуса a мы получим, что потенциал φ у самой его поверхности подчиняется уравнению
φₐ= φₐ₀ / (1 – β cos α)
где φₐ₀ – потенциал рядом с поверхностью заряда (на бесконечно малом расстоянии от нее), когда заряд покоится относительно среды.
Это, по-видимому, означает, что при движении заряда его поверхностная плотность не одинакова в разных точках или объемная плотность неодинакова во всем объеме заряда. Теоретически, это можно проверить, если исследовать движение заряженной сферы в вакууме и перераспределение зарядов на ее поверхности. Причем измерять надо не напряженность электрического поля вокруг заряда (потому что одни и те же изменения поля можно интерпретировать по-разному, как в рамках «классической» теории, так и в рамках моей теории), а само распределение зарядов (или токи) на поверхности сферы. Но при тех скоростях, которые достижимы в настоящее время, зарегистрировать такое перераспределение зарядов будет не так просто.
Отредактировано: Yuri Rus - 02 дек 2019 04:01:08

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Давайте, наконец, рассмотрим вывод самого уравнения Лиенара-Вихерта. Где же там могут быть ошибки?
Будем опять следовать Фейнману. Я перескажу его доказательство своими словами, чтобы сделать его более ясным и усилить некоторые моменты. Дело в том, что некоторые ключевые вещи он прямо не говорит, о них можно только догадаться по его рисункам и формулам. Если я неправильно понял Фейнмана, прошу меня поправить. Уравнение Лиенара-Вихерта играет ключевую роль для вывода преобразований Лоренца и для теории относительности, поэтому этот вопрос заслуживает того, чтобы на него потратить какое-то время, чтобы добиться полной ясности.
Итак, Фейнман сначала оговаривает, что точечный заряд – это очень маленький заряженный шарик с плотностью заряда ρ(x, y, z). Потом пишет:

И ниже:

Сейчас я перехожу к своей интерпретации аргументации Фейнмана, поскольку у него это не сформулировано достаточно явно и четко.
Потенциал φ в точке (1) в момент времени t является суммой единичных волн потенциала, каждая из которых была излучена в разные моменты времени и на разных расстояниях от точки (1). Причем за то время, пока сигнал от самого дальнего элемента заряда дойдет до самого ближнего элемента, этот ближний элемент успеет пройти какое-то расстояние. Вместо стороны куба a, эффективная длина заряда становится a/(1 – v/c), причем считается, что плотность заряда ρ не меняется. Судя по рисунку 21.7, логика здесь такая: объем (не заряд, а именно объем пространства!) размерами a ⨯ a ⨯ a/(1 – v/c), через который проходит заряд за время путешествия сигнала от самого дальнего до самого ближнего участка заряда, разбивается на некоторое число элементов толщиной w. Затем сигналы от этих элементов объема суммируются следующим образом: сначала к сумме добавляется сигнал (единичная волна потенциала) от самого дальнего элемента объема, где в этот момент находится первый элемент заряда с толщиной w и плотностью заряда ρ. Потом мы переходим к следующему элементу объема толщиной w и добавляем к сумме его сигнал, излученный в следующий момент времени (чтобы сигналы от всех элементов объема достигли точки (1) одновременно). При этом, первый элемент заряда, который был раньше в первом элементе объема, успел частично сместиться во второй элемент объема. Допустим, скорость заряда v = 0.9 c и мы измеряем потенциал спереди от движущегося заряда. Это означает, что 90% второго элемента объема будут заполнены первым элементом заряда – и он опять вносит вклад в сигнал, который добавляется к общей сумме. Оставшиеся 10% объема второго элемента объема заполнены вторым элементом заряда, так что плотность заряда остается той же самой – ρ. В следующий момент времени, все тот же первый элемент заряда займет 80% третьего элемента объема – и внесет 80% вклада в сигнал от него, второй элемент заряда внесет 20% вклада. Плотность заряда та же. И т.д.
Поскольку мне пару раз напоминали, что ГА – это политико-экономический форум и не место длядискуссий физики, предложу политико-экономическую аналогию этому процессу. На злобу дня: представьте себе, что М. Каддафи прогнал всех аль-каидовцев из Ливии и они собрались на острове Лампедуза. И требуют еды и воды, мы же, мол, для вас демократию и гуманитарные бомбардировки, то есть ценности, защищали. И привезли добросердечные итальянцы им еды и воды на 10 дней на 10 грузовиках, и сказали: «Становитесь в очереди к грузовикам. Каждый получит рацион на один день только. Завтра получите рацион еще на один день». А хитрые аль-каидовцы, зная, что итальянцы их друг от друга отличить не смогут, каждый заняли 10 очередей ко всем 10 грузовикам. И в итоге итальянцы обнаружили, что все грузовики оказались пустыми всего за один день. И каждый день они привозят по 10 грузовиков, и всегда те загадочным образом опустошаются, хотя они очень следят, чтобы на руки выдавать только по одному рациону. А раскормленные аль-каидовцы требуют еще и еще.
Думаю, требование политико-экономичности я выполнил? Можно вернуться к физике?
Для v = 0.9 c, поправочный (ЛВД) множитель равен 1 / (1 – 0.9) = 10. Это означает, что каждый элемент заряда внесет свой вклад в сигнал не один раз, а 10 раз, потому что суммирование производится не по элементам заряда, а по элементам объема, так что каждый элемент заряда успевает «отметиться» в разных элементах объема (вклад всех, кроме первого и последнего элементов заряда, сначала растет от 10% до 100%, потом опять убывает до 10%). В этом и заключается смысл уравнения Лиенара-Вихерта.
Мда. Свистнуто, не спорю, действительно свистнуто, но, если говорить беспристрастно, свистнуто очень средне! Отметьте, это уравнение – один из краеугольных камней современной физики, на нем стоит теория относительности. А само это уравнение стоит на идее, что суммировать сигнал от элементов заряда надо не по самим элементам заряда, а по тому объему пространства, через который они прошли за время путешествия сигнала от дальнего конца заряда к ближнему, причем суммирование производится таким образом, что каждый элемент заряда учитывается не один, а много раз.
Не слишком ли это шаткое основание для современной физики?
Я думаю, что намного больше физического смысла имеет иная процедура суммирования – по самим элементам заряда. При этой процедуре, каждый элемент заряда вносит вклад в общий потенциал только один раз. Допустим, для v = 0.9 c, суммирование будет выглядеть следующим образом:
◘■■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□■◘■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□■■◘■■□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■◘■□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■■◘
В первый момент времени, сигнал излучается самым дальним элементом заряда. Во второй момент времени, сигнал излучается вторым элементом заряда, который за это время успел сместиться на расстояние 9w. В третий момент времени, сигнал излучается третьим элементом заряда, который за это время успел сместиться еще на расстояние 9w. И так далее. В итоге, каждый элемент заряда внесет свой вклад в суммарный потенциал только один раз и уравнение для потенциала будет, все-таки,
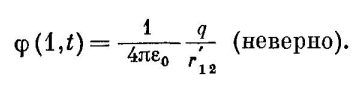
На первой странице ветки, я написал:
Я буду в основном говорить о волнах и волновом уравнении. Отмечу, что уравнения динамики жидкости и твердого тела в классической механике обычно выражаются в двух формах – лагранжевой и эйлеровой. Уравнения в форме Лагранжа описывают движения индивидуальной частицы жидкости или твердого тела (точнее, некоторого элемента объема, состоящего из многих частиц). Координаты (x, y, z) частицы считаются функциями времени и трех параметров (a, b, c), в качестве которых часто выбираются координаты частицы при t = 0. Уравнения в форме Эйлера описывают то, что происходит в некоторой точке пространства (x, y, z) (точнее, с неким бесконечно малым элементом длины, поверхности или объема) на протяжении некоторого промежутка времени. Рассматриваются силы, скорости, смещения и т.д. применительно именно к этому малому элементу, и для него выводятся дифференциальные уравнения. Для полного описания поведения системы, задаются еще начальные и граничные условия.
Я предлагаю третий подход. Вместо того, чтобы рассматривать силы, скорости и смещения некого элемента среды (или некой частицы), расположенного в произвольной точке пространства, мы будем начинать анализ распространения волн с их источника. Есть источник, он создает какую-то силу, действующую на окружающие его элементы среды (которые не расположены где-то далеко, а прямо и непосредственно контактируют с источником), эта сила вызывает смещение этих элементов, которые приобретают ускорение, скорость, далее они воздействуют на соседние с ними элементы среды, и т.д. Причем, что важно с физической точки зрения – источник создает не единичную волну, которая затем распространяется по покоящейся среде, а множество волн, непрерывно генерирует их. Кроме того, если мы хотим обсудить теорию относительности, мы должны рассмотреть движение источника относительно среды.
Суммирование по элементам заряда, то есть по элементам источника, и есть пример этого третьего подхода.
Это очень важный момент. Уравнение Лиенара-Вихерта является типичным уравнением в форме Эйлера – и решено в полном соответствии с правилами решений этих уравнений мат. физики. Мне не попадалась его запись в форме Лагранжа, но, надо думать, и в том виде его решение было бы точно таким же, поскольку, вроде бы, принципиальных расхождений между подходами Лагранжа и Эйлера до сих пор не наблюдалось. Та ошибка, на которую я указываю, в рамках мат. физики ошибкой вовсе не считается. Мат. физика полна подобных уравнений – таковы очень многие уравнения динамики материальных сред, в частности, гидродинамики и электродинамики. Я имею в виду те уравнения, где один и тот же элемент массы или заряда, благодаря своему движению относительно элемента пространства, учитывается не один раз, а k раз, где k может быть и больше, и меньше единицы.
Это только одна из серьезных ошибок мат. физики, которые, как я считаю, и привели к тому, что почти вся физика (и классическая тоже) как наука к настоящему времени неверна.
Я опирался на подход Фейнмана к выводу уравнения Лиенара-Вихерта, но в учебниках встречаются и другие подходы. Допустим, в книге Беккер Р. «Теория Электричества. Том 2. Электронная теория» (1941), на стр. 61-65 приводится другой вариант этого вывода. В книге Джексон Дж. «Классическая электродинамика» (1965), на стр. 509-510 приводится вывод этого уравнения при помощи функций Грина и δ-функции Дирака. Я приведу цитаты в конце этого сообщения.
Смысл всех этих подходов, при внешних различиях, один и тот же. Все они исходят из того, что вклад элементов заряда надо учитывать много раз, по мере их прохождения через разные элементы объема. Изложение Фейнмана мне просто нравится больше – из-за большей наглядности и «физичности». В отличие от многих физиков, он стремился найти и объяснить именно физический смысл уравнений физики, не считал, что уравнения и есть вся физика.
Итак, подытожим. Уравнение Лиенара-Вихерта неверно – запаздывание не приводит к появлению дополнительного множителя у потенциала, распространяющегося от источника. Тем не менее, дополнительный (по сравнению с покоящимся источником) множитель может появиться – из-за изменения формы заряда при движении или перераспределения плотности заряда; для источника звука – из-за изменения плотности среды вокруг источника. Именно это изменение плотности заряда или среды вокруг источника и передается во все стороны – в «нулевом приближении», без искажений. Запаздывание же к этому никакого отношения не имеет.
Беккер Р. «Теория Электричества. Том 2. Электронная теория» (1941), стр. 61-65:





Джексон Дж. «Классическая электродинамика» (1965), стр. 509-510:


Будем опять следовать Фейнману. Я перескажу его доказательство своими словами, чтобы сделать его более ясным и усилить некоторые моменты. Дело в том, что некоторые ключевые вещи он прямо не говорит, о них можно только догадаться по его рисункам и формулам. Если я неправильно понял Фейнмана, прошу меня поправить. Уравнение Лиенара-Вихерта играет ключевую роль для вывода преобразований Лоренца и для теории относительности, поэтому этот вопрос заслуживает того, чтобы на него потратить какое-то время, чтобы добиться полной ясности.
Итак, Фейнман сначала оговаривает, что точечный заряд – это очень маленький заряженный шарик с плотностью заряда ρ(x, y, z). Потом пишет:

И ниже:

Сейчас я перехожу к своей интерпретации аргументации Фейнмана, поскольку у него это не сформулировано достаточно явно и четко.
Потенциал φ в точке (1) в момент времени t является суммой единичных волн потенциала, каждая из которых была излучена в разные моменты времени и на разных расстояниях от точки (1). Причем за то время, пока сигнал от самого дальнего элемента заряда дойдет до самого ближнего элемента, этот ближний элемент успеет пройти какое-то расстояние. Вместо стороны куба a, эффективная длина заряда становится a/(1 – v/c), причем считается, что плотность заряда ρ не меняется. Судя по рисунку 21.7, логика здесь такая: объем (не заряд, а именно объем пространства!) размерами a ⨯ a ⨯ a/(1 – v/c), через который проходит заряд за время путешествия сигнала от самого дальнего до самого ближнего участка заряда, разбивается на некоторое число элементов толщиной w. Затем сигналы от этих элементов объема суммируются следующим образом: сначала к сумме добавляется сигнал (единичная волна потенциала) от самого дальнего элемента объема, где в этот момент находится первый элемент заряда с толщиной w и плотностью заряда ρ. Потом мы переходим к следующему элементу объема толщиной w и добавляем к сумме его сигнал, излученный в следующий момент времени (чтобы сигналы от всех элементов объема достигли точки (1) одновременно). При этом, первый элемент заряда, который был раньше в первом элементе объема, успел частично сместиться во второй элемент объема. Допустим, скорость заряда v = 0.9 c и мы измеряем потенциал спереди от движущегося заряда. Это означает, что 90% второго элемента объема будут заполнены первым элементом заряда – и он опять вносит вклад в сигнал, который добавляется к общей сумме. Оставшиеся 10% объема второго элемента объема заполнены вторым элементом заряда, так что плотность заряда остается той же самой – ρ. В следующий момент времени, все тот же первый элемент заряда займет 80% третьего элемента объема – и внесет 80% вклада в сигнал от него, второй элемент заряда внесет 20% вклада. Плотность заряда та же. И т.д.
Поскольку мне пару раз напоминали, что ГА – это политико-экономический форум и не место для
Думаю, требование политико-экономичности я выполнил? Можно вернуться к физике?
Для v = 0.9 c, поправочный (ЛВД) множитель равен 1 / (1 – 0.9) = 10. Это означает, что каждый элемент заряда внесет свой вклад в сигнал не один раз, а 10 раз, потому что суммирование производится не по элементам заряда, а по элементам объема, так что каждый элемент заряда успевает «отметиться» в разных элементах объема (вклад всех, кроме первого и последнего элементов заряда, сначала растет от 10% до 100%, потом опять убывает до 10%). В этом и заключается смысл уравнения Лиенара-Вихерта.
Мда. Свистнуто, не спорю, действительно свистнуто, но, если говорить беспристрастно, свистнуто очень средне! Отметьте, это уравнение – один из краеугольных камней современной физики, на нем стоит теория относительности. А само это уравнение стоит на идее, что суммировать сигнал от элементов заряда надо не по самим элементам заряда, а по тому объему пространства, через который они прошли за время путешествия сигнала от дальнего конца заряда к ближнему, причем суммирование производится таким образом, что каждый элемент заряда учитывается не один, а много раз.
Не слишком ли это шаткое основание для современной физики?
Я думаю, что намного больше физического смысла имеет иная процедура суммирования – по самим элементам заряда. При этой процедуре, каждый элемент заряда вносит вклад в общий потенциал только один раз. Допустим, для v = 0.9 c, суммирование будет выглядеть следующим образом:
◘■■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□■◘■■■□□□□□□□□□□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□■■◘■■□□□□□□□□□□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■◘■□□□□□□□□□
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□■■■■◘
В первый момент времени, сигнал излучается самым дальним элементом заряда. Во второй момент времени, сигнал излучается вторым элементом заряда, который за это время успел сместиться на расстояние 9w. В третий момент времени, сигнал излучается третьим элементом заряда, который за это время успел сместиться еще на расстояние 9w. И так далее. В итоге, каждый элемент заряда внесет свой вклад в суммарный потенциал только один раз и уравнение для потенциала будет, все-таки,
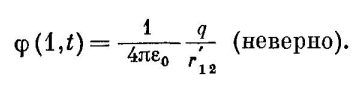
На первой странице ветки, я написал:
Я буду в основном говорить о волнах и волновом уравнении. Отмечу, что уравнения динамики жидкости и твердого тела в классической механике обычно выражаются в двух формах – лагранжевой и эйлеровой. Уравнения в форме Лагранжа описывают движения индивидуальной частицы жидкости или твердого тела (точнее, некоторого элемента объема, состоящего из многих частиц). Координаты (x, y, z) частицы считаются функциями времени и трех параметров (a, b, c), в качестве которых часто выбираются координаты частицы при t = 0. Уравнения в форме Эйлера описывают то, что происходит в некоторой точке пространства (x, y, z) (точнее, с неким бесконечно малым элементом длины, поверхности или объема) на протяжении некоторого промежутка времени. Рассматриваются силы, скорости, смещения и т.д. применительно именно к этому малому элементу, и для него выводятся дифференциальные уравнения. Для полного описания поведения системы, задаются еще начальные и граничные условия.
Я предлагаю третий подход. Вместо того, чтобы рассматривать силы, скорости и смещения некого элемента среды (или некой частицы), расположенного в произвольной точке пространства, мы будем начинать анализ распространения волн с их источника. Есть источник, он создает какую-то силу, действующую на окружающие его элементы среды (которые не расположены где-то далеко, а прямо и непосредственно контактируют с источником), эта сила вызывает смещение этих элементов, которые приобретают ускорение, скорость, далее они воздействуют на соседние с ними элементы среды, и т.д. Причем, что важно с физической точки зрения – источник создает не единичную волну, которая затем распространяется по покоящейся среде, а множество волн, непрерывно генерирует их. Кроме того, если мы хотим обсудить теорию относительности, мы должны рассмотреть движение источника относительно среды.
Суммирование по элементам заряда, то есть по элементам источника, и есть пример этого третьего подхода.
Это очень важный момент. Уравнение Лиенара-Вихерта является типичным уравнением в форме Эйлера – и решено в полном соответствии с правилами решений этих уравнений мат. физики. Мне не попадалась его запись в форме Лагранжа, но, надо думать, и в том виде его решение было бы точно таким же, поскольку, вроде бы, принципиальных расхождений между подходами Лагранжа и Эйлера до сих пор не наблюдалось. Та ошибка, на которую я указываю, в рамках мат. физики ошибкой вовсе не считается. Мат. физика полна подобных уравнений – таковы очень многие уравнения динамики материальных сред, в частности, гидродинамики и электродинамики. Я имею в виду те уравнения, где один и тот же элемент массы или заряда, благодаря своему движению относительно элемента пространства, учитывается не один раз, а k раз, где k может быть и больше, и меньше единицы.
Это только одна из серьезных ошибок мат. физики, которые, как я считаю, и привели к тому, что почти вся физика (и классическая тоже) как наука к настоящему времени неверна.
Я опирался на подход Фейнмана к выводу уравнения Лиенара-Вихерта, но в учебниках встречаются и другие подходы. Допустим, в книге Беккер Р. «Теория Электричества. Том 2. Электронная теория» (1941), на стр. 61-65 приводится другой вариант этого вывода. В книге Джексон Дж. «Классическая электродинамика» (1965), на стр. 509-510 приводится вывод этого уравнения при помощи функций Грина и δ-функции Дирака. Я приведу цитаты в конце этого сообщения.
Смысл всех этих подходов, при внешних различиях, один и тот же. Все они исходят из того, что вклад элементов заряда надо учитывать много раз, по мере их прохождения через разные элементы объема. Изложение Фейнмана мне просто нравится больше – из-за большей наглядности и «физичности». В отличие от многих физиков, он стремился найти и объяснить именно физический смысл уравнений физики, не считал, что уравнения и есть вся физика.
Итак, подытожим. Уравнение Лиенара-Вихерта неверно – запаздывание не приводит к появлению дополнительного множителя у потенциала, распространяющегося от источника. Тем не менее, дополнительный (по сравнению с покоящимся источником) множитель может появиться – из-за изменения формы заряда при движении или перераспределения плотности заряда; для источника звука – из-за изменения плотности среды вокруг источника. Именно это изменение плотности заряда или среды вокруг источника и передается во все стороны – в «нулевом приближении», без искажений. Запаздывание же к этому никакого отношения не имеет.
Беккер Р. «Теория Электричества. Том 2. Электронная теория» (1941), стр. 61-65:





Джексон Дж. «Классическая электродинамика» (1965), стр. 509-510:


Отредактировано: Yuri Rus - 02 дек 2019 04:10:55

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: Yuri Rus от 23.05.2011 20:46:23
Казалось бы, векторы x, из начала координат к произвольной точке пространства (x, y, z) в момент времени t, и x', из начала координат к источнику (x’, y’, z’) в запаздывающий момент времени t’, являются точно такими же переменными, как у меня (x, y, z), для произвольной точки пространства в момент t, и (ξ, η, ζ), для положения источника в момент ԏ. Что еще нужно?
И тем не менее, разница есть, и существенная. Я говорю, что все 6 пространственных координат и 2 временные являются переменными и относиться к ним надо соответственно. Например, включать их частные производные в определение полного дифференциала и полной производной по времени. Например, интегрировать по всем 6 пространственным координатам, а не только по 3 из них; по 2 временным координатам, а не по одной. Между прочим, для запаздывающих функций обычно интегрируют по запаздывающим координатам источника и по запаздывающему времени, а не по координатам точки наблюдения в настоящий момент времени.
После этого, я хотел написать пару фраз, но забыл:
При этом, координаты (x, y, z) и время t вообще не учитываются (они являются параметрами, в Вашей трактовке?). А если речь идет о сравнении "замороженного" поля частицы в точке (x, y, z) в момент t и в точке (x + vdt, y, z) в момент t + dt, то внезапно забывают про переменные координаты (x', y', z' ) и время t' и перепрыгивают на x, y, z, t.
Я внесу это исправление в оригинальное сообщение.
Отредактировано: Yuri Rus - 10 июн 2012 07:01:34

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Ну что, померла так померла?
Я правильно понял, что такие длинные тексты, с хотя и очень простыми, но слишком многими формулами, ни у кого сил нет читать и вникать?
Могу почти без формул, на пальцах, качественно. Формулы могу добавить потом, когда суть будет понята.
Так?
Я правильно понял, что такие длинные тексты, с хотя и очень простыми, но слишком многими формулами, ни у кого сил нет читать и вникать?
Могу почти без формул, на пальцах, качественно. Формулы могу добавить потом, когда суть будет понята.
Так?

Карма: +113.64
Регистрация: 15.10.2008
Сообщений: 1,039
Читатели: 0
Регистрация: 15.10.2008
Сообщений: 1,039
Читатели: 0
Да, пожалуй, так будет удобнее.
Я Физфак университета в закончил почти 20 лет назад, тяжело восстанавливать в памяти формулы, ооооочень медленно дело идёт.
Я Физфак университета в закончил почти 20 лет назад, тяжело восстанавливать в памяти формулы, ооооочень медленно дело идёт.
Карма: +9.19
Регистрация: 12.01.2008
Сообщений: 1,126
Читатели: 0
Регистрация: 12.01.2008
Сообщений: 1,126
Читатели: 0
Цитата: Yuri Rus от 26.05.2011 08:58:37
Ну что, померла так померла?
Я правильно понял, что такие длинные тексты, с хотя и очень простыми, но слишком многими формулами, ни у кого сил нет читать и вникать?
Могу почти без формул, на пальцах, качественно. Формулы могу добавить потом, когда суть будет понята.
Так?
Лично для меня -- именно так. Сижу жду резюме на человеческом языке, чтобы понять, имеет ли смысл разбираться в формулах.

Москва
24 года
Карма: +0.16
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0
Регистрация: 28.01.2011
Сообщений: 36
Читатели: 0
Цитата: Yuri Rus от 26.05.2011 08:58:37
Ну что, померла так померла?
Я правильно понял, что такие длинные тексты, с хотя и очень простыми, но слишком многими формулами, ни у кого сил нет читать и вникать?
Могу почти без формул, на пальцах, качественно. Формулы могу добавить потом, когда суть будет понята.
Так?
Юрий, большинству конечно сложно, но в любом случае вы, со своей стороны, делаете правильные действия (действия направленные на развитие физики; а критика это тоже развитие), и не ваша вина в том что большая часть не всё понимает, ваши действия в любом случае, мне кажется, в правильном русле...
Скажу тоже за себя: идёт сложно (7 лет назад закончил Физтех), но я думаю, что не у всех так.
и, конечно, добавить объяснений на пальцах было бы отлично!


moscow
Карма: +788.72
Регистрация: 09.01.2011
Сообщений: 12,560
Читатели: 11
Регистрация: 09.01.2011
Сообщений: 12,560
Читатели: 11
Цитата: PublicJoke от 26.05.2011 12:00:10
Лично для меня -- именно так. Сижу жду резюме на человеческом языке, чтобы понять, имеет ли смысл разбираться в формулах.
Вполне правильно озвучен подход.
Озвучте "генеральную линию", так сказать.
Это вполне вписывается в стандартный формат любого исследовательского материала.
Без резюме никак. Можно и в формате введения/преамбулы.
Здесь конечно есть своя доля риска - самоназванных охранителей догматики ставшего уже фактически религией современности "научного сциентизма" довольно много.
Но если уж решились огласить публично нечто придётся смириться с подобным явлением: тут главное их не прикармливать. ;)
А кроме того ГА хоть и отличается изрядным процентом представительства "физико-математиков" (так уж повелось начиная с основателя) открыта для всех слоёв широкой публики.
Народ безмолвствует. А счастлив ли Народ?...

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Хорошо. Давайте я расскажу краткую историю того, как я пришел к выводу, что математика физики фундаментально неверна и физику нужно строить заново, почти с нуля.
В 1982 г. я окончил ФТФ НЭТИ (ныне НГТУ), специальность «инженерная электрофизика», кафедра электрофизических установок и ускорителей (она была расположена не в самом НЭТИ, а в ИЯФ в Академгородке, и лекции нам читали в основном сотрудники ИЯФ). Никаких сомнений в истинности теории относительности у меня не было – я с ней познакомился еще в девятом классе и все мне было понятно. Пишу об этом только потому, что большинство физиков свято убеждено, что критиковать теорию относительности могут лишь те, кто в ней не разобрался, не может примирить ее со своим "обыденным опытом". На самом деле, ничего сложного в ТО нет – и те, кто имеет дело с ускорителями, менее всего склонны в ней сомневаться. Как раз перед окончанием, мне пришли в голову некоторые идеи и я был очень захвачен ими, настолько, что не занимался даже своим дипломом. Потом понял, что без бумажки ты букашка и за несколько дней написал дипломную работу.
Идеи эти были связаны с волновыми пакетами. В начале 20-х годов, это было популярное направление развития квантовой механики, но потом от него отказались из-за, казалось бы, непреодолимой проблемы дисперсии пакетов, их расплывания со временем. В итоге, была принята вероятностная интерпретация волн, а вкупе с принципом неопределенности задавать вопросы типа «что такое частица», «где она находится», «не является ли поле частью частицы» и пр., стало неприличным. Утверждалось, что в квантовой механике такие вопросы не имеют смысла.
Я к этому подошел по другому – сначала я рассматривал не двигающуюся частицу, а покоящуюся, и представлял частицу как «стоячий волновой пакет». Здесь сразу же получалось, что огибающая этого пакета – 1 / r, как у потенциала Кулоновского или гравитационного поля. Далее у меня вытекало, что этот волновой пакет – знакопеременный, с центральным пиком и чередованием положительных и отрицательных областей по мере удаления от центра. Это давало совершенно иное объяснение, почему протоны в ядре не разлетаются в разные стороны. Никакого сильного взаимодействия не требовалось. Получалось естественное объяснение и многих других явлений.
Однако, при релятивистских скоростях это поле, неотделимое от частицы, должно было сокращаться в γ раз. А ведь отрицательно заряженные частицы в известной нам части Вселенной, в основном, представлены электронами, тогда как положительно заряженные частицы – протонами, массы которых различаются в 1836 раз. Большинство из этих частиц сосредоточено в звездах, с температурами от нескольких тысяч градусов на поверхности до многих миллионов градусов в центре, так что, во-первых, практически все эти частицы ионизированы, во-вторых, они двигаются с довольно высокими скоростями. Причем средние скорости электронов во много раз больше, чем у протонов, именно потому, что у них меньше масса. Скорости протонов в центре звезды могут быть порядка сотен и даже тысяч километров в секунду (скорости молекул газа при комнатной температуре - несколько сотен метров в секунду), тогда как скорости электронов будут намного больше и релятивистские поправки для них будут вполне заметными. Это означает, что никакой компенсации положительных и отрицательных полей (слово "полей" было пропущено и вставлено позже, после замечания читателя wow) зарядов, двигающихся с разными скоростями, не будет. Электрическое поле протонов было бы значительно сильнее поля электронов (см. ниже) – у всех звезд. Чего, как известно, не наблюдается. Электрического поля во Вселенной в целом практически нет, поля положительно и отрицательно заряженных частиц компенсируют друг друга с большой точностью. Вселенная в целом электрически нейтральна.
То есть, вроде бы, моя теория противоречила наблюдаемым фактам. Но я быстро понял, что этот аргумент – отсутствие компенсации электрических полей движущихся частиц – в полной мере относится к самой ТО. Он не имеет никакого отношения к моей теории, он является неизбежным следствием именно ТО. Ведь электрическое поле движущейся частицы сокращается в γ раз согласно ТО, а не согласно моей теории. Именно этот аргумент заставил меня задуматься о том, что ТО должна быть неверна. Он, в принципе, достаточно очевиден и, надо полагать (?), кто-то раньше его уже высказывал. Но я его нигде не встречал.
Я начал читать книги по ТО и искать работы критиков ТО, чтобы разобраться, где же здесь могут быть ошибки. В критиках-то ТО недостатка как раз нет, но их аргументы меня не удовлетворили. Чтобы разобраться, мне пришлось залезать в основы физики, в основы математики все глубже и глубже. В итоге, я пришел к выводу, что математика физики содержит очень многие фундаментальные (базовые, исходные, элементарные) ошибки. Причем эти ошибки образуют замкнутый порочный круг, поддерживают друг друга. В основном, они были совершены еще в XVIII-XIX веках, такими учеными, как Эйлер, Дюамель и др. Потом они закостенели, стали догмами – стали законами, из которых выводится всё остальное. См. это мое сообщение.
Дело еще в том, что основы математики физики были заложены не физиками, а математиками. А они думают совсем по-другому. Абстрактно. Математический способ построения любой математической теории (или «естественной науки» типа физики, химии, биологии, и пр.) таков: принимаются некие аксиомы, постулаты, из которых затем выводятся следствия. Если речь идет о чисто математической теории, то этим все и ограничивается, теория лишь все более усложняется, по своим внутренним законам. В случае естественной науки, следствия теории сравниваются с практикой, с экспериментом. В случае несовпадения с теорией, выдвигаются дополнительные постулаты, вводятся новые сущности (например, от идеальной жидкости переходят к сжимаемой, вязкой). Но исходные постулаты при этом почти никогда не пересматриваются – они «отлиты в граните». В частности, еще и потому, что над последующими поколениями довлеет авторитет классиков.
При этом, для математика каждая такая теория, основанная на неких исходных аксиомах, имеет самоценность. Неважно, соответствует ли она реальности – ведь математическая модель, если она правильно построена и непротиворечива, справедлива сама по себе. Лобачевский построил первую неэвклидову геометрию. Потом появились другие геометрии, а сейчас их я даже не знаю сколько (вообще говоря, бесконечно большое число, но только некоторая часть из них исследована). И все они, с точки зрения математики, справедливы. Но с точки зрения физики, это не так (должно быть не так) – только ОДНА из них действительно соответствует реальному миру.
Проблема в том, что «правильная» математическая теория, даже если она не соответствует реальному миру, выглядит «слишком убедительно». Ведь в ней нет формальных математических ошибок! Есть исходные постулаты, из которых выводятся все остальные формулы. Все логично, самосогласованно, непротиворечиво – математически. И не соответствует реальности. Но и это не беда – если обнаружено несоответсвие предсказаний математической теории экспериментальным фактам, всегда можно добавить еще один «эпицикл». Так и было совершено большинство так называемых крупнейших физических открытий ХХ века. Обнаружены всякие все более «тонкие эффекты».
Пересматривать надо не верхние этажи (а теория относительности и квантовая механика относятся к верхним этажам), а фундамент физики, ее исходные постулаты. Только так можно вырваться из порочного круга.
По мере того, как я залезал в этот фундамент, я обнаруживал все новые и новые ошибки, связанные между собой в тот самый порочный круг. Сейчас я вообще не знаю, можно ли полагаться хоть на какие-то формулы, законы физики. Я нахожусь в XVIII веке – только недавно были изобретены дифференциальное и интегральное исчисления. Все нужно строить заново. Я знаю, что сам я, один, не смогу построить новое здание физики. Если я смогу убедить кого-то еще, что математика физики неверна, тогда это можно будет сделать.
Я, конечно, не ограничиваюсь тем, что тыкаю пальцем в ошибки. Я предлагаю что-то взамен. Но я работаю с самым фундаментом – а за последние 300 лет здание физики все-таки несколько выросло. Заново возводить надо очень много этажей. Я считаю это большим плюсом – потому что те, кто построят эти этажи, могут рассчитывать сами стать классиками науки. То есть у них будет личная заинтересованность – а если быть реалистами, это является решающим в поведении людей. Так что, в принципе, за судьбу новой физики я спокоен – если, конечно, смогу доказать, что я прав. А доказать это наиболее эффективным образом я смогу, если экспериментально получу искусственную гравитацию. Тогда за месяц вся физика будет переписана молодыми и амбициозными физиками.
Кроме моей предыстории и некоторых общих рассуждений о математике и физике, я здесь высказал главный аргумент, который заставил меня прийти к выводу, что теория относительности неверна. Вот он:
При движении заряженной частицы, ее электрическое поле в направлении движения сокращается в γ раз, где
γ = 1 / (1 - v²/c²)½
У протонов и альфа-частиц γ относительно невелика, ей можно пренебречь – по сравнению с γ электронов. Электроны двигаются в разных направлениях и в каждый момент времени у части электронов имеется сжатие электрического поля по любому выбранному направлению, так что суммарное отрицательное электрическое поле электронов центра будет сжато в Аγ раз, где А – некоторый коэффициент, меньший единицы. Положительное поле протонов и альфа-частиц не имеет значительного сжатия и не может компенсировать ослабленное электрическое поле намного более быстрых электронов. Таким образом, центр звезды будет иметь очень сильное положительное поле протонов. Это вызовет приток дополнительных электронов в центр звезды и отталкивание протонов и альфа-частиц от центра на периферию Попав в центр, дополнительные электроны приобретут высокие скорости и их поле тоже сожмется. Тем не менее, в итоге в центре будет достигнут баланс полей электронов и протонов/альфа-частиц.
На периферии же звезды будет огромный избыток протонов и альфа-частиц. Они будут отталкиваться друг от друга с огромной силой и вылетать с поверхности звезды. В конечном итоге, если регистрировать электрическое поле звезды снаружи, звезда будет выглядеть электрически нейтральной. Но вне звезд, будет большой избыток протонов и альфа-частиц – и не будет достаточного количества электронов, чтобы компенсировать этот избыток. То есть Вселенная в целом была бы положительно заряжена. Заряжена не чуть-чуть, а очень сильно. Дисбаланс был бы, вероятно, на малые доли процента от общего числа протонов и электронов: пусть одна миллионная процента. Пусть одна миллиардная. Пусть одна триллионная. Пусть даже 10-20, 10-30. Даже это - слишком много. Потому что Кулоновское поле очень сильное – в 10³⁶ раз сильнее, чем гравитационное взаимодействие двух протонов. На фоне этого дисбаланса, гравитационное поле вообще не было бы заметно. Дисбаланс положительно заряженных частиц не был бы заметен, только если он значительно меньше, чем 10⁻³⁶. Но быстрые электроны в звездах должны привести к на много порядков большему дисбалансу. Нет, дисбаланса этого, безусловно, нет – а если бы ТО была справедлива, он должен был бы быть.
Давайте как отправную точку возьмем этот аргумент и обсудим его. Он достаточно простой. Есть вопросы, возражения?
P.S. Для новых читателей ветки: этот аргумент ошибочный. Ниже Pnb указал мне на допущенную ошибку. Была длительная дискуссия, большую часть которой я в итоге решил удалить, чтобы не загромождать ветку и не заставлять новых читеталей тратить свое время на детали ошибочного аргумента.
В 1982 г. я окончил ФТФ НЭТИ (ныне НГТУ), специальность «инженерная электрофизика», кафедра электрофизических установок и ускорителей (она была расположена не в самом НЭТИ, а в ИЯФ в Академгородке, и лекции нам читали в основном сотрудники ИЯФ). Никаких сомнений в истинности теории относительности у меня не было – я с ней познакомился еще в девятом классе и все мне было понятно. Пишу об этом только потому, что большинство физиков свято убеждено, что критиковать теорию относительности могут лишь те, кто в ней не разобрался, не может примирить ее со своим "обыденным опытом". На самом деле, ничего сложного в ТО нет – и те, кто имеет дело с ускорителями, менее всего склонны в ней сомневаться. Как раз перед окончанием, мне пришли в голову некоторые идеи и я был очень захвачен ими, настолько, что не занимался даже своим дипломом. Потом понял, что без бумажки ты букашка и за несколько дней написал дипломную работу.
Идеи эти были связаны с волновыми пакетами. В начале 20-х годов, это было популярное направление развития квантовой механики, но потом от него отказались из-за, казалось бы, непреодолимой проблемы дисперсии пакетов, их расплывания со временем. В итоге, была принята вероятностная интерпретация волн, а вкупе с принципом неопределенности задавать вопросы типа «что такое частица», «где она находится», «не является ли поле частью частицы» и пр., стало неприличным. Утверждалось, что в квантовой механике такие вопросы не имеют смысла.
Я к этому подошел по другому – сначала я рассматривал не двигающуюся частицу, а покоящуюся, и представлял частицу как «стоячий волновой пакет». Здесь сразу же получалось, что огибающая этого пакета – 1 / r, как у потенциала Кулоновского или гравитационного поля. Далее у меня вытекало, что этот волновой пакет – знакопеременный, с центральным пиком и чередованием положительных и отрицательных областей по мере удаления от центра. Это давало совершенно иное объяснение, почему протоны в ядре не разлетаются в разные стороны. Никакого сильного взаимодействия не требовалось. Получалось естественное объяснение и многих других явлений.
Однако, при релятивистских скоростях это поле, неотделимое от частицы, должно было сокращаться в γ раз. А ведь отрицательно заряженные частицы в известной нам части Вселенной, в основном, представлены электронами, тогда как положительно заряженные частицы – протонами, массы которых различаются в 1836 раз. Большинство из этих частиц сосредоточено в звездах, с температурами от нескольких тысяч градусов на поверхности до многих миллионов градусов в центре, так что, во-первых, практически все эти частицы ионизированы, во-вторых, они двигаются с довольно высокими скоростями. Причем средние скорости электронов во много раз больше, чем у протонов, именно потому, что у них меньше масса. Скорости протонов в центре звезды могут быть порядка сотен и даже тысяч километров в секунду (скорости молекул газа при комнатной температуре - несколько сотен метров в секунду), тогда как скорости электронов будут намного больше и релятивистские поправки для них будут вполне заметными. Это означает, что никакой компенсации положительных и отрицательных полей (слово "полей" было пропущено и вставлено позже, после замечания читателя wow) зарядов, двигающихся с разными скоростями, не будет. Электрическое поле протонов было бы значительно сильнее поля электронов (см. ниже) – у всех звезд. Чего, как известно, не наблюдается. Электрического поля во Вселенной в целом практически нет, поля положительно и отрицательно заряженных частиц компенсируют друг друга с большой точностью. Вселенная в целом электрически нейтральна.
То есть, вроде бы, моя теория противоречила наблюдаемым фактам. Но я быстро понял, что этот аргумент – отсутствие компенсации электрических полей движущихся частиц – в полной мере относится к самой ТО. Он не имеет никакого отношения к моей теории, он является неизбежным следствием именно ТО. Ведь электрическое поле движущейся частицы сокращается в γ раз согласно ТО, а не согласно моей теории. Именно этот аргумент заставил меня задуматься о том, что ТО должна быть неверна. Он, в принципе, достаточно очевиден и, надо полагать (?), кто-то раньше его уже высказывал. Но я его нигде не встречал.
Я начал читать книги по ТО и искать работы критиков ТО, чтобы разобраться, где же здесь могут быть ошибки. В критиках-то ТО недостатка как раз нет, но их аргументы меня не удовлетворили. Чтобы разобраться, мне пришлось залезать в основы физики, в основы математики все глубже и глубже. В итоге, я пришел к выводу, что математика физики содержит очень многие фундаментальные (базовые, исходные, элементарные) ошибки. Причем эти ошибки образуют замкнутый порочный круг, поддерживают друг друга. В основном, они были совершены еще в XVIII-XIX веках, такими учеными, как Эйлер, Дюамель и др. Потом они закостенели, стали догмами – стали законами, из которых выводится всё остальное. См. это мое сообщение.
Дело еще в том, что основы математики физики были заложены не физиками, а математиками. А они думают совсем по-другому. Абстрактно. Математический способ построения любой математической теории (или «естественной науки» типа физики, химии, биологии, и пр.) таков: принимаются некие аксиомы, постулаты, из которых затем выводятся следствия. Если речь идет о чисто математической теории, то этим все и ограничивается, теория лишь все более усложняется, по своим внутренним законам. В случае естественной науки, следствия теории сравниваются с практикой, с экспериментом. В случае несовпадения с теорией, выдвигаются дополнительные постулаты, вводятся новые сущности (например, от идеальной жидкости переходят к сжимаемой, вязкой). Но исходные постулаты при этом почти никогда не пересматриваются – они «отлиты в граните». В частности, еще и потому, что над последующими поколениями довлеет авторитет классиков.
При этом, для математика каждая такая теория, основанная на неких исходных аксиомах, имеет самоценность. Неважно, соответствует ли она реальности – ведь математическая модель, если она правильно построена и непротиворечива, справедлива сама по себе. Лобачевский построил первую неэвклидову геометрию. Потом появились другие геометрии, а сейчас их я даже не знаю сколько (вообще говоря, бесконечно большое число, но только некоторая часть из них исследована). И все они, с точки зрения математики, справедливы. Но с точки зрения физики, это не так (должно быть не так) – только ОДНА из них действительно соответствует реальному миру.
Проблема в том, что «правильная» математическая теория, даже если она не соответствует реальному миру, выглядит «слишком убедительно». Ведь в ней нет формальных математических ошибок! Есть исходные постулаты, из которых выводятся все остальные формулы. Все логично, самосогласованно, непротиворечиво – математически. И не соответствует реальности. Но и это не беда – если обнаружено несоответсвие предсказаний математической теории экспериментальным фактам, всегда можно добавить еще один «эпицикл». Так и было совершено большинство так называемых крупнейших физических открытий ХХ века. Обнаружены всякие все более «тонкие эффекты».
Пересматривать надо не верхние этажи (а теория относительности и квантовая механика относятся к верхним этажам), а фундамент физики, ее исходные постулаты. Только так можно вырваться из порочного круга.
По мере того, как я залезал в этот фундамент, я обнаруживал все новые и новые ошибки, связанные между собой в тот самый порочный круг. Сейчас я вообще не знаю, можно ли полагаться хоть на какие-то формулы, законы физики. Я нахожусь в XVIII веке – только недавно были изобретены дифференциальное и интегральное исчисления. Все нужно строить заново. Я знаю, что сам я, один, не смогу построить новое здание физики. Если я смогу убедить кого-то еще, что математика физики неверна, тогда это можно будет сделать.
Я, конечно, не ограничиваюсь тем, что тыкаю пальцем в ошибки. Я предлагаю что-то взамен. Но я работаю с самым фундаментом – а за последние 300 лет здание физики все-таки несколько выросло. Заново возводить надо очень много этажей. Я считаю это большим плюсом – потому что те, кто построят эти этажи, могут рассчитывать сами стать классиками науки. То есть у них будет личная заинтересованность – а если быть реалистами, это является решающим в поведении людей. Так что, в принципе, за судьбу новой физики я спокоен – если, конечно, смогу доказать, что я прав. А доказать это наиболее эффективным образом я смогу, если экспериментально получу искусственную гравитацию. Тогда за месяц вся физика будет переписана молодыми и амбициозными физиками.
Кроме моей предыстории и некоторых общих рассуждений о математике и физике, я здесь высказал главный аргумент, который заставил меня прийти к выводу, что теория относительности неверна. Вот он:
При движении заряженной частицы, ее электрическое поле в направлении движения сокращается в γ раз, где
γ = 1 / (1 - v²/c²)½
У протонов и альфа-частиц γ относительно невелика, ей можно пренебречь – по сравнению с γ электронов. Электроны двигаются в разных направлениях и в каждый момент времени у части электронов имеется сжатие электрического поля по любому выбранному направлению, так что суммарное отрицательное электрическое поле электронов центра будет сжато в Аγ раз, где А – некоторый коэффициент, меньший единицы. Положительное поле протонов и альфа-частиц не имеет значительного сжатия и не может компенсировать ослабленное электрическое поле намного более быстрых электронов. Таким образом, центр звезды будет иметь очень сильное положительное поле протонов. Это вызовет приток дополнительных электронов в центр звезды и отталкивание протонов и альфа-частиц от центра на периферию Попав в центр, дополнительные электроны приобретут высокие скорости и их поле тоже сожмется. Тем не менее, в итоге в центре будет достигнут баланс полей электронов и протонов/альфа-частиц.
На периферии же звезды будет огромный избыток протонов и альфа-частиц. Они будут отталкиваться друг от друга с огромной силой и вылетать с поверхности звезды. В конечном итоге, если регистрировать электрическое поле звезды снаружи, звезда будет выглядеть электрически нейтральной. Но вне звезд, будет большой избыток протонов и альфа-частиц – и не будет достаточного количества электронов, чтобы компенсировать этот избыток. То есть Вселенная в целом была бы положительно заряжена. Заряжена не чуть-чуть, а очень сильно. Дисбаланс был бы, вероятно, на малые доли процента от общего числа протонов и электронов: пусть одна миллионная процента. Пусть одна миллиардная. Пусть одна триллионная. Пусть даже 10-20, 10-30. Даже это - слишком много. Потому что Кулоновское поле очень сильное – в 10³⁶ раз сильнее, чем гравитационное взаимодействие двух протонов. На фоне этого дисбаланса, гравитационное поле вообще не было бы заметно. Дисбаланс положительно заряженных частиц не был бы заметен, только если он значительно меньше, чем 10⁻³⁶. Но быстрые электроны в звездах должны привести к на много порядков большему дисбалансу. Нет, дисбаланса этого, безусловно, нет – а если бы ТО была справедлива, он должен был бы быть.
Давайте как отправную точку возьмем этот аргумент и обсудим его. Он достаточно простой. Есть вопросы, возражения?
P.S. Для новых читателей ветки: этот аргумент ошибочный. Ниже Pnb указал мне на допущенную ошибку. Была длительная дискуссия, большую часть которой я в итоге решил удалить, чтобы не загромождать ветку и не заставлять новых читеталей тратить свое время на детали ошибочного аргумента.
Отредактировано: Yuri Rus - 08 июн 2011 07:03:59

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: Dobryаk
У всех свои пророки. Я не знаю вывода потенциалов Лиенарда-Вихерта проще и однозначнее, чем описано в томе 2 "Теория поля" Ландау-Лифшица (у меня старое издание, в нем это параграф 63). Нет никаких сомнений в том, что Ландау с Лифшицем не путаются в переменных и умеют дифференцировать, что классические ответы (63.8) и (63.9) правильные, проверены на опыте и никаких других на белом свете не существует. Это если оставаться в рамках классической теории поля.
В-общем, опровержение потенциалов Лиенарда-Вихерта не та точка опоры, подперев о которую ломик как рычаг, можно перевернуть основы мироздания с ног на голову.
Я посмотрел том 2. Вывод Ландау-Лифшица основан на теории относительности, сделан в рамках искривленного пространства-времени Минковского, при помощи 4-векторов. Соответственно, он не имеет никакой доказательной силы, поскольку потенциалы Лиенара-Вихерта там уже заложены в геометрию этого пространства, в его исходные аксиомы (точнее, в геометрию заложены преобразования Лоренца, а потенциал Лиенара-Вихерта однозначно выводится из этих преобразований, точно так же, как и преобразования Лоренца выводятся из потенциала Лиенара-Вихерта).
Кроме того, не забывайте, что потенциалы эти были выведены в рамках классической электродинамики. Без 4-векторов - и без функции Грина с δ-функцией. Эти более поздние способы получения той же самой формулы должны ставиться под сомнение уже потому, что их авторы имели перед собой такую цель - добиться соответствия с первоначальным решением, как минимум подсознательно подгоняли свой ответ под ранее известный. Потому анализировать надо именно первоначальный метод вывода, а не более поздние, использующие иной мат. аппарат, зачастую специально созданный для этой именно цели (как аппарат СТО).
Отредактировано: Yuri Rus - 27 май 2011 01:55:54

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Цитата: mozgi
Я далеко не специалист в астрофизике поэтому не стану делать вид, что досконально понимаю поведение вырожденного электронного газа в недрах звезд, однако очень настораживает самое последнее Ваше утверждение, о том, что электроны и протоны сталкиваются как обычные частицы газа, это откуда следует? Особенно про поля непонятно. Если мы об электрическом поле, то у электронов и протонов вроде как разный знак заряда, как минимум. Что за поля такие заставляют их вести себя по отношению друг к другу как упругие тела? Этот момент совершенно неясен.
Я вообще-то не специалист по плазме или процессам внутри звезд и читал об этом последний раз много лет назад. Но то, что я читал, однозначно говорит о том, что скорости электронов внутри звезд во много раз больше скоростей ионов.
Вообще-то, даже очень короткий поиск в Гугле дал бы Вам ответы на Ваши вопросы. Даже Википедия имеет эти ответы. И есть масса книг, конечно. Library Genesis, допустим.
О Кулоновском взаимодействии электронов и ионов в плазме:
http://en.wikipedia.…_collision
Взаимодействие электронов и ионов (где поле каждой частицы влияет на все соседние частицы) в плазме, конечно, отличается от столкновений нейтральных частиц в газе.
In a plasma a Coulomb collision rarely results in a large deflection. The cumulative effect of the many small angle collisions, however, is often larger than the effect of the few large angle collisions...
Fast particles are "slippery" and thus dominate many transport processes. The efficiency of velocity-matched interactions is also the reason that fusion products tend to heat the electrons rather than (as would be desirable) the ions. If an electric field is present, the faster electrons feel less drag and become even faster in a "run-away" process.
In passing through a field of ions with density n, an electron will have many such encounters simultaneously, with various impact parameters and directions. The cumulative effect can be described as a diffusion of the perpendicular momentum.
О плазме:
http://ru.wikipedia.…0%BC%D0%B0
http://en.wikipedia.…physics%29
В неравновесной плазме электронная температура существенно превышает температуру ионов. Это происходит из-за различия в массах иона и электрона, которое затрудняет процесс обмена энергией.
В равновесной плазме обе температуры равны. Поскольку для осуществления процесса ионизации необходимы температуры, сравнимые с потенциалом ионизации, равновесная плазма обычно является горячей (с температурой больше нескольких тысяч K).
Понятие высокотемпературная плазма употребляется обычно для плазмы термоядерного синтеза, который требует температур в миллионы K.
тепловая скорость электрона, формула для оценки скорости электронов при распределении Максвелла. Средняя скорость, наиболее вероятная скорость и среднеквадратичная скорость отличаются от этого выражения лишь множителями порядка единицы:

тепловая скорость иона, формула для оценки скорости ионов при распределении Максвелла:

---------
Из формул для скоростей электронов и протонов, предполагая, что они имеют одинаковую температуру (здесь она выражена в eV), видно, что скорости электронов в 43 раза больше, чем скорости протонов, и в 86 раз больше, чем скорости альфа-частиц. Для релятивистских электронов, это различие, конечно, меньше.
Отредактировано: Yuri Rus - 27 май 2011 06:56:39

64 года
Карма: +394.05
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Регистрация: 20.10.2008
Сообщений: 4,380
Читатели: 1
Модератор ветки
Допустим, температура в центре звезды равна 20 миллионов градусов.
Из соотношения 1 eV --> 11600 К (см. ссылку о плазме в предыдущем сообщении), получим (синим исправленный текст, первоначально была ошибка):
20 000 000 К --> 1724 eV
Подставив 1724 eV вместо Te в формуле

получим скорость электрона
ve = 17400 км/сек
Это вполне значимая скорость, для которой релятивистские поправки уже весьма ощутимы.
β = v/c = 0.058
γ ≈ 1 + β² / 2 = 1.0017
Конечно, это γe только в центре звезды (для одной тысячной массы звезды? одной десятитысячной?). Основная масса электронов имеет намного меньшие скорости и для них релятивистский эффект сжатия электрического поля намного меньше.
Это неважно - сравнивать нам ведь надо с гравитационным полем, которое в 10³⁶ раз слабее, чем Кулоновское.
Давайте сравним релятивистский эффект для поверхности звезды - скажем, 6000 К:
ve = 300 км/сек
γe = 1.0000005
Тоже вполне заметно.
По сравнению с гравитационным полем, это тоже даст более чем заметную разницу между положительным полем ионов и отрицательным полем электронов. Скажем, для 6000 К эта разница будет примерно 0.0000005 от поля всех протонов и альфа-частиц верхних слоев звезды. Это чудовищная сила.
Конечно, все частицы и поля в любой момент времени стремятся к положению равновесия, такой дисбаланс никогда не вознинет даже на долю секунды. Просто (если ТО верна) по мере нагревания центра звезды к нему будет стремиться всё больше электронов, а всё больше ионов будут двигаться от центра и вскоре покинут поверхность звезды, которая в целом останется почти нейтральной. Так или иначе, в межзвездном пространстве будет накапливаться все больше протонов и альфа-частиц, для которых просто нет достаточного числа электронов. С другой стороны, до образования звезд никакого избытка электронов, который компенсировался бы потом выбрасыванием "лишних" протонов, быть не могло - такой отрицательно заряженный газ никогда не сформировал бы газопылевое облако и не сжался бы в прото-звезду.
Из соотношения 1 eV --> 11600 К (см. ссылку о плазме в предыдущем сообщении), получим (синим исправленный текст, первоначально была ошибка):
20 000 000 К --> 1724 eV
Подставив 1724 eV вместо Te в формуле

получим скорость электрона
ve = 17400 км/сек
Это вполне значимая скорость, для которой релятивистские поправки уже весьма ощутимы.
β = v/c = 0.058
γ ≈ 1 + β² / 2 = 1.0017
Конечно, это γe только в центре звезды (для одной тысячной массы звезды? одной десятитысячной?). Основная масса электронов имеет намного меньшие скорости и для них релятивистский эффект сжатия электрического поля намного меньше.
Это неважно - сравнивать нам ведь надо с гравитационным полем, которое в 10³⁶ раз слабее, чем Кулоновское.
Давайте сравним релятивистский эффект для поверхности звезды - скажем, 6000 К:
ve = 300 км/сек
γe = 1.0000005
Тоже вполне заметно.
По сравнению с гравитационным полем, это тоже даст более чем заметную разницу между положительным полем ионов и отрицательным полем электронов. Скажем, для 6000 К эта разница будет примерно 0.0000005 от поля всех протонов и альфа-частиц верхних слоев звезды. Это чудовищная сила.
Конечно, все частицы и поля в любой момент времени стремятся к положению равновесия, такой дисбаланс никогда не вознинет даже на долю секунды. Просто (если ТО верна) по мере нагревания центра звезды к нему будет стремиться всё больше электронов, а всё больше ионов будут двигаться от центра и вскоре покинут поверхность звезды, которая в целом останется почти нейтральной. Так или иначе, в межзвездном пространстве будет накапливаться все больше протонов и альфа-частиц, для которых просто нет достаточного числа электронов. С другой стороны, до образования звезд никакого избытка электронов, который компенсировался бы потом выбрасыванием "лишних" протонов, быть не могло - такой отрицательно заряженный газ никогда не сформировал бы газопылевое облако и не сжался бы в прото-звезду.
Отредактировано: Yuri Rus - 08 июн 2011 07:08:08

Карма: +2.39
Регистрация: 26.10.2008
Сообщений: 1,224
Читатели: 3
Регистрация: 26.10.2008
Сообщений: 1,224
Читатели: 3
Ознакомившись с некоторыми доводами, я сделал вывод.
1. Неумение объяснить простым доступным языком, на примере одной координаты, хотя бы как у того же Феймана, что наводит на мысль, что Фейман досконально понимает о чем пишет, а автор не совсем.
2. Построение своей некой «идеальной» теории, могущей, якобы объяснить практически все противоречия современной физики, что наравне с громкими заявлениями о низвержении всех основ, наводит на мысль о непонимании философии развития жизни и науки в частности.
3. Это влечет за собой коренную методологическую ошибку, автор берется описать систему изнутри, просто подставляя другие параметры, хотя не трудно понять, что это в принципе невозможно. Надо подниматься на следующую ступень понимания реальности.
Я уже давал ссылку о попытки проделать такой шаг. Это пишут физики, которые реально двигаются вверх в понимании вселенной, они опираются на современные опыты и многие парадоксы нелокальности и дуализма разрешаются на этих уровнях.
Вот просто небольшая выдержка:
Весь материальный классический мир, согласно квантовой теории, не является основой реальности. Совокупная квантовая реальность гораздо богаче и шире. Классический мир — это лишь «картинка», видимость, внешнее проявление одной из сторон квантовой реальности.
Нелокальный источник реальности, из которого «проецируется» наш плотный мир — это довольно глубокое понятие. Может ввести в заблуждение сам термин «нелокальный». Речь идет о квантовой нелокальности, которая не имеет отношения к волнам, полям, к классическим энергиям любого вида и типа. Квантовая нелокальность вообще не может быть описана классической физикой.
Нелокальный квантовый источник реальности — это мир, в котором вообще нет никакой массы и потоков энергии. Это пустота, которая, тем не менее, содержит в себе всю полноту классических (тварных) энергий в нелокальной суперпозиции. Все тварные энергии (в том числе на тонких уровнях) как бы компенсируют друг друга и в своей совокупности образуют Всеобъемлющую Пустоту. Пустоту лишь в том смысле, что этот мир невидим в своей целостности. На уровне Универсума остается только одна возможность — оперировать квантовой информацией, кроме которой там ничего больше и нет.
Нелокальный источник реальности не является материальным, поскольку в нем нет массы и энергии, и вообще в нем нет ничего, что имело бы отношение к классической физике. Можно условно назвать его единым информационным полем, которое содержит в себе информацию о внутренней структуре Универсума, а декогеренция — это своеобразное проявление этой информации в виде той или иной классической реальности (проекции) — проявление «картинки», которое сопровождается потоками тварных энергий (в том числе на тонких уровнях, где выше мера квантовой запутанности).
Нет общей классической реальности, общего мира, единого для всех частей (подсистем). Квантовая теория позволяет гораздо шире взглянуть на окружающую реальность, и, в отличие от классической физики, которая предполагает, что есть некий единый, общий для всех материальный мир, говорит о том, что могут существовать другие миры из тварных энергий различной плотности (различные по мере квантовой запутанности). В моей интерпретации декогеренция, как фундаментальный физический процесс, имеет место не только среди плотных энергий привычного нам мира классической реальности, но и других более «тонких» энергий. Там «собираются» уже другие «картинки», другие проекции реальности.
У них уже реально проходят опыты по "телепортации" частиц. Вполне обсуждаемы проявления изменеий гравитации, как другие проявления нелокального источника реальности. И главное никаких основ они не низвергают, а просто двигаются вверх в познании мира.
1. Неумение объяснить простым доступным языком, на примере одной координаты, хотя бы как у того же Феймана, что наводит на мысль, что Фейман досконально понимает о чем пишет, а автор не совсем.
2. Построение своей некой «идеальной» теории, могущей, якобы объяснить практически все противоречия современной физики, что наравне с громкими заявлениями о низвержении всех основ, наводит на мысль о непонимании философии развития жизни и науки в частности.
3. Это влечет за собой коренную методологическую ошибку, автор берется описать систему изнутри, просто подставляя другие параметры, хотя не трудно понять, что это в принципе невозможно. Надо подниматься на следующую ступень понимания реальности.
Я уже давал ссылку о попытки проделать такой шаг. Это пишут физики, которые реально двигаются вверх в понимании вселенной, они опираются на современные опыты и многие парадоксы нелокальности и дуализма разрешаются на этих уровнях.
Вот просто небольшая выдержка:
Весь материальный классический мир, согласно квантовой теории, не является основой реальности. Совокупная квантовая реальность гораздо богаче и шире. Классический мир — это лишь «картинка», видимость, внешнее проявление одной из сторон квантовой реальности.
Нелокальный источник реальности, из которого «проецируется» наш плотный мир — это довольно глубокое понятие. Может ввести в заблуждение сам термин «нелокальный». Речь идет о квантовой нелокальности, которая не имеет отношения к волнам, полям, к классическим энергиям любого вида и типа. Квантовая нелокальность вообще не может быть описана классической физикой.
Нелокальный квантовый источник реальности — это мир, в котором вообще нет никакой массы и потоков энергии. Это пустота, которая, тем не менее, содержит в себе всю полноту классических (тварных) энергий в нелокальной суперпозиции. Все тварные энергии (в том числе на тонких уровнях) как бы компенсируют друг друга и в своей совокупности образуют Всеобъемлющую Пустоту. Пустоту лишь в том смысле, что этот мир невидим в своей целостности. На уровне Универсума остается только одна возможность — оперировать квантовой информацией, кроме которой там ничего больше и нет.
Нелокальный источник реальности не является материальным, поскольку в нем нет массы и энергии, и вообще в нем нет ничего, что имело бы отношение к классической физике. Можно условно назвать его единым информационным полем, которое содержит в себе информацию о внутренней структуре Универсума, а декогеренция — это своеобразное проявление этой информации в виде той или иной классической реальности (проекции) — проявление «картинки», которое сопровождается потоками тварных энергий (в том числе на тонких уровнях, где выше мера квантовой запутанности).
Нет общей классической реальности, общего мира, единого для всех частей (подсистем). Квантовая теория позволяет гораздо шире взглянуть на окружающую реальность, и, в отличие от классической физики, которая предполагает, что есть некий единый, общий для всех материальный мир, говорит о том, что могут существовать другие миры из тварных энергий различной плотности (различные по мере квантовой запутанности). В моей интерпретации декогеренция, как фундаментальный физический процесс, имеет место не только среди плотных энергий привычного нам мира классической реальности, но и других более «тонких» энергий. Там «собираются» уже другие «картинки», другие проекции реальности.
У них уже реально проходят опыты по "телепортации" частиц. Вполне обсуждаемы проявления изменеий гравитации, как другие проявления нелокального источника реальности. И главное никаких основ они не низвергают, а просто двигаются вверх в познании мира.
Отредактировано: wow - 27 май 2011 08:57:57
Сейчас на ветке:
3,
Модераторов: 0,
Пользователей: 0,
Гостей: 0,
Ботов: 3