Тред №319458

Давайте рассмотрим, как распространяются волны в рамках «нулевого приближения». «Нулевое приближение» означает, что последовательные волны от движущегося источника не взаимодействуют; каждая единичная волна, испущенная в точке  (ξ, η, ζ)  в момент времени  ԏ,  распространяется радиально с фазовой скоростью  с  в покоящейся среде (в первом приближении, среда уже не покоится, но об этом мы будем говорить позже).

Именно так, собственно, и рассматривает распространение волн «официальная физика».  С ее точки зрения, если источник покоится, векторы фазовой скорости  с  и лучей   r  всех волн направлены радиально из точки, где находится источник. Если источник движется, векторы  с  и  r  каждой излучаемой им единичной волны направлены по-прежнему радиально, но теперь не из точки, где находится источник в данный момент, а из точки, где был источник в момент излучения этой волны. Траектории, образуемые векторами  с  и  r  для каждой волны – прямые линии как для покоящегося, так и для движущегося источника.

Чтобы проиллюстрировать это, еще раз посмотрим на апплет для эффекта Доплера:

http://www.astro.ubc…ppler.html

Этот апплет показывает распространение фронтов волн от движущегося источника в системе отсчета, где среда покоится. Я сам не могу сделать апплет (я не программист), где распространение волн показано для системы отсчета, связанной с источником. Но это, наверно, и не требуется – достаточно слегка поворачивать голову по мере движения источника и представить себе, что источник покоится, а среда движется (встречный ветер со скоростью  –V_и). Можно сказать, что тем самым вы мысленно проделаете преобразования Галилея.

Авторы апплета, я уверен, использовали алгебраическое волновое уравнение типа

(x – V_иt)² + y² + z² = c²(t – ԏ)²  или  r – r_и = c(t – ԏ),

а не искали решение неоднородного дифференциального уравнения. Это было бы в тысячи раз сложнее, а результат, казалось бы, будет одинаков – зачем же мучиться?

Мгновенный снимок волн от движущегося источника, который я уже приводил, выглядит так:
 

 
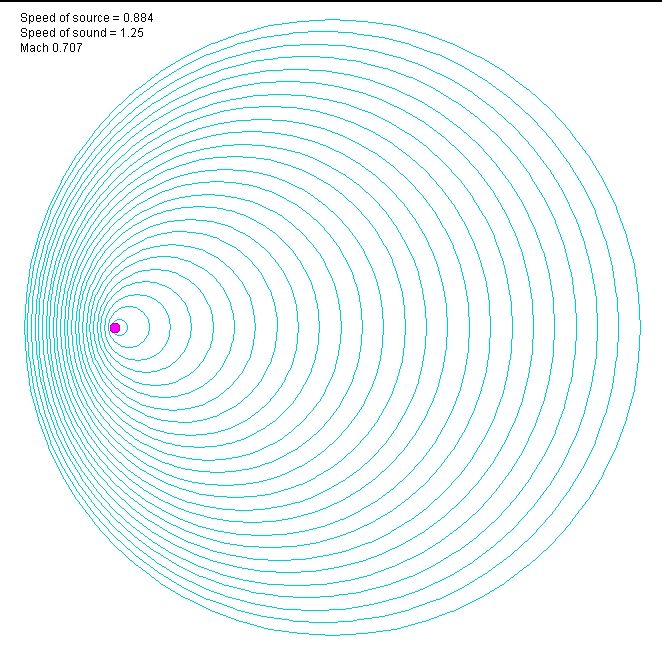
Запомним эту картинку, она нам еще не раз пригодится. Картинка эта, безусловно, имеет физический смысл (если кто-то не согласен, объясните, почему). Это я и имел в виду, когда ранее писал, что это простенькое алгебраическое волновое уравнение полезно использовать как «контроль на физический смысл», для качественной оценки волновых процессов.

Обратите внимание, еще раз – все волны сферические. Не сплюснутые в  γ  раз. В системе отсчета движущегося относительно среды источника, волны не выглядят так, как будто источник находится в покоящейся среде (где волны радиально распространяются из одного центра с одной и той же скоростью во всех направлениях). Эти сферические волны сдувает встречный ветер, поэтому спереди и сзади от источника волны выглядят отнюдь не симметрично.

Заметьте также, что если мы сделаем мгновенный снимок всех волн в какой-то момент времени, то этот снимок (форма каждой единичной волны и их расположение друг относительно друга) будет выглядеть абсолютно одинаково в обеих системах отсчета, покоящейся и движущейся. Это очень важно. Можно даже сформулировать это правило в виде закона:

Волновое уравнение инвариантно относительно преобразований Галилея. Все члены волнового уравнения должны выглядеть одинаково во всех инерциальных системах отсчета.

Откуда это следует? Ранее я писал, что волновое уравнение выводится из Второго Закона Ньютона и по сути является другой формой записи Второго Закона, эквивалентно ему. Каждый член волнового уравнения представляет собой ту или иную силу. А сила инвариантна относительно преобразований Галилея – вектор силы одинаков в любой инерциальной системе отсчета.

Приведу цитату из книги  Гальцов Д.В., Грац Ю.В., Жуковский В.Ч. «Классические Поля», 1991, стр. 6-7:
 


  
Авторы этой книги, разумеется, ничего не пишут (и не подозревают, скорее всего) об инвариантности волнового уравнения относительно преобразований Галилея. Я привел эту цитату только для демонстрации самих преобразований Галилея, чтобы у читателя не было подозрений, что я что-то исказил. Инвариантность волнового уравнения – это мое утверждение. В учебниках физики я его не встречал.

Оно отнюдь не тривиально, потому что физика полна волновых уравнений в частных производных, которые выглядят совершенно иначе в разных системах отсчета. В частности, они описывают сжатие волн в  γ  раз, причем даже в нерелятивистском случае. Не будем пока трогать теорию относительности, ее постулаты и доказательства. Но к звуковым-то волнам преобразования Лоренца, сжатие в  γ  раз, казалось бы, не могут применяться? Это же – противоречит здравому смыслу?

Здравому смыслу, здравому смыслу. Тоже мне – аргумент. Когда это было препятствием для «настоящей физики» (помните выражение Нильса Бора о теории, достаточно сумасшедшей, чтобы быть правильной)? Физика, как известно, гордится тем, что теория относительности и квантовая механика противоречат здравому смыслу. Противоречие здравому смыслу буквально считается важнейшим достижением современной физики, доказательством высоты человеческого гения – ну как же, необузданный полет воображения привел к таким математическим формулам, физического смысла которых ни один человек не может себе представить. Можно только жонглировать математическими манипуляциями, а пытаться поставить им в соответствие какой-то мысленный образ, какие-то материальные (в смысле классической физики) объекты и процессы – признак глупости и непонимания физики. Есть только мат (math) – за него и держись.

Так вот, если последовательно, по-честному применять математические методы физики к переходу из одной инерциальной системы в другую, то никуда от гаммы и от сжатия звуковых волн вы не денетесь. Потому что они заложены в математическом фундаменте физики, а не в постулатах теории относительности или уравнениях Максвелла.

Продемонстрирую это на примере очень полезной для наших целей книги Блохинцева Д.И. «Акустика неоднородной движущейся среды» (1981), стр. 84-86:
 



 
Посмотрите на уравнения (3.12), (3.13) и (3.13'). Для источника, движущегося с дозвуковой скоростью  v,  автор получил сжатие звуковых волн в  γ  раз, где

γ = 1/(1 – (v/c) ²)^½ ,   c – скорость звука, а не света.

Эти сжатые волны выглядят как центрально-симметричные эллипсоиды:
 

 

 
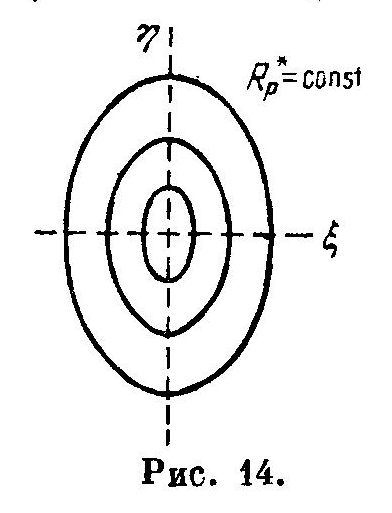
Это, опять же, полностью аналогично теории относительности.

Проверим уравнения Блохинцева на физический смысл. Посмотрим еще раз на апплет для эффекта Доплера, на мгновенный снимок всех волн от движущегося источника, на наш «контроль на физический смысл»  r – r_и = c(t – ԏ),  и сравним с уравнениями Блохинцева. Имеет сжатие звуковых волн в  γ  раз какой-то физический смысл?

Категорически – нет, нет, нет! Ни в каком случае и никогда! Звуковые волны не бывают зеленого цвета эллиптическими,  это вас кто-то обманул. Им полагается быть сферическими. В системе отсчета движущегося источника, их сдувает встречный ветер, из-за чего волновая картина (совокупность последовательных волн) не может быть центрально-симметричной. Даже если математика второй свежести утверждает обратное.

Сейчас физика – это не более чем раздел математики, играет подчиненную роль. А должно быть наоборот. Не может математика считаться истинной, если она тухлая явным образом противоречит реальному миру. Да, математик, основанных на разных аксиомах, может быть много. Но реальный мир, в котором мы живем, - только один. И потому истинной является только та математика, которая действительно соответствует этому реальному миру.

Поскольку, я предполагаю, читать меня будут не только физики, хочу сказать пару слов об авторе. Вот немного о Д.И. Блохинцеве (1908-1979) из Википедии:

«Окончил физический факультет Московского государственного университета (1930). Преподавал там же (с 1936 — профессор, затем заведующий кафедрой теоретической ядерной физики). Был создателем Отделения ядерной физики на физическом факультете МГУ. В 1935—1947 годах работал также в Физическом институте АН СССР (ФИАН). С 1947 года — директор научно-исследовательской лаборатории в Обнинске, на базе которой под его руководством создан Физико-энергетический институт. Руководитель Лаборатории «В» Министерства внутренних дел СССР (выполнение постановления «О проектировании и строительстве объекта 627»), позже на её базе создан ИЯИ РАН.

Был инициатором создания Объединённого института ядерных исследований (ОИЯИ) в Дубне. В 1956 году Комитет Полномочных Представителей одиннадцати стран единогласно избрал его первым директором этого института. В 1956—1965 годах — директор ОИЯИ, с 1965 года — директор Лаборатории теоретической физики ОИЯИ.

Научная деятельность

Работы посвящены теории твердого тела, физике полупроводников, оптике, акустике, квантовой механике и квантовой электронике, ядерной физике, теории ядерных реакторов, квантовой теории поля, физике элементарных частиц, философским и методологическим вопросам физики.
…
В 1944 году построил, исходя из уравнений газогидродинамики, теорию звуковых явлений в движущихся и неоднородных средах, получив уравнения акустики самого общего вида (уравнения Блохинцева), на основе которых вывел ряд акустических законов, объяснил и рассчитал разнообразные акустические явления в движущихся и неоднородных средах (в том числе турбулентных), касающихся, с одной стороны, механизма генерирования шума, а с другой — методов и средств его приема. Сформулировал уравнения геометрической акустики.

И многое другое.»

Так что не думайте, что я где-то раскопал побитую молью книжонку никому не известного автора и радостно хихикаю, что обнаружил там махонькую ошибочку. Это – фундамент данного раздела физики.