Тред №325722

Попробую качественно пересказать некоторые ранее написанные вещи – немного другими словами и значительно короче. Совсем без формул обойтись нельзя, но я не буду давать их детальный вывод (он уже дан), только их качественную интерпретацию, их смысл. Здесь даже следует говорить не о физическом смысле, а о геометрическом, которому был придан глобальный физический смысл, совершенно им не заслуженный.

Давайте я уже введу более короткие обозначения для системы отсчета источника и системы отсчета покоящейся среды: СОИ и СОПС. Даже выделю их цветом и размером, на случай, если кто в будущем забудет, чтобы легче было найти их в тексте: 

СОИ – СОПС

Мы имеем некий источник волн, который двигается с постоянной скоростью по прямой линии, по оси  х.  Рассмотрим одну единичную волну (импульс, если угодно), которую этот источник излучил в нулевой момент времени  t = 0.  В СОПС, распространение этой волны в последовательные моменты времени будет выглядеть следующим образом:
 

 
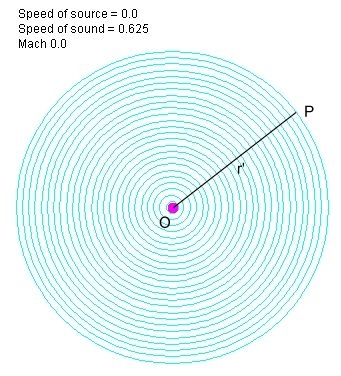
В момент  t,  эта волна достигает точки Р. Расстояние от точки О, в которой находился источник в момент излучения этой единичной волны, до точки Р обозначено как  r'.

В СОИ, распространение этой же единичной волны в последовательные моменты времени будет выглядеть иначе:
 

 
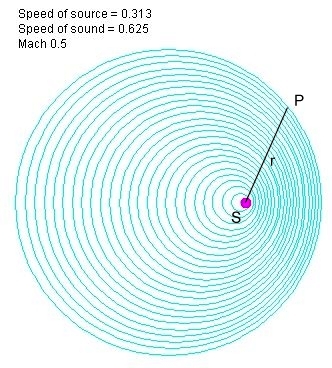
В СОИ, расстояние от источника (точка S) до точки Р обозначено как  r.

За то время, пока эта единичная волна достигла точки Р, в СОПС источник сместился на расстояние OS. Это расстояние равно скорости источника  v,  умноженной на время  t, которое понадобилось волне, чтобы пройти расстояние  r'.  Легко увидеть, что время это равно расстоянию  r’,  разделенному на скорость волны  с.  То есть источник сместился на расстояние  vt = vr' / c.

В координатах СОПС, расстояние  r'  равно

r’ = (x² + y² + z²)^½

В СОИ, вместо  х  введем координату  u.  Расстояние  r  равно

r = (u² + y² + z²)^½

При этом, координата  u  СОИ связана с  координатой  х  СОПС следующим соотношением:

u = x – vt

Далее, нам известно, что некий потенциал, характеризующий наши волны, зависит от расстояния  r'  следуюшим образом:

g = f / r’

То есть  g  зависит от расстояния до источника в момент излучения волны, а не от расстояния до источника в тот момент, где он окажется, когда волна наконец-то придет в некую отдаленную точку.

Возникает вопрос: как нам выразить потенциал  g  в координатах СОИ, а не в координатах СОПС (r'  выражен именно в координатах СОПС)?

Это довольно простая геометрическая задачка. Как уже сказано,  u  и  х  связаны соотношением

u = x – vt

Отсюда

x = u + vt = u + vr' / c

Подставив это вместо  х  в выражение для  расстояния  r':

r’² = (u + vr' / c)² + y² + z²

и решив обычное квадратное уравнение относительно  r',  мы сможем выразить  r’  в координатах СОИ:

r' = (β u + (u² + (1 – β²) (y² + z²))^½) / (1 – β²)

где  β = v/c.

Мы видим, что в этом выражении появилась «знаменитая» гамма:

γ = 1 / (1 – β²)^½

Но появилась она здесь из чистой геометрии (простейшей, заметьте). Никакой «физики» в ней нет.

Вернемся к потенциалу  g.  В координатах СОИ, когда мы подставим выражение для  r',  g  будет выглядеть как:

g = f / r’ = f (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))^½)

Немного неуклюжее выражение, да с него не воду пить. Подчеркну еще раз: это выражение для  g,  записанное относительно координат источника (сам источник находится в начале координат СОИ).

Теперь мы, по каким-то соображениям, решили, что даже в СОПС нам неудобно записывать выражение для  g  относительно запаздывающих координат источника (координат той точки, где был источник в момент излучения волны). Мы хотим выразить  g  в любой точке в момент времени  t  (то есть в настоящий момент) через координаты источника в этот же момент времени  t.  Как нам это сделать?

Очень просто: мы возьмем уже готовое выражение для  g  в координатах источника в СОИ и подставим везде  x – vt  вместо  u:

g = f (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))^½)

Вуаля – мы имеем выражение для  g  в СОПС в любой момент времени. Мы его получили при помощи двойного применения преобразования Галилея для координат: сначала использовали  x = u + vt,  чтобы перейти из СОПС в СОИ, затем обратный переход при помощи  u = x – vt.

Как будут выглядеть поверхности, соответствующие фиксированным значениям  g  в определенный момент времени? То есть эквипотенциальные поверхности, где  g = g₁,  g = g₂,  g = g₃,  g = g₄,  и т.д.? Вот так:
 

 
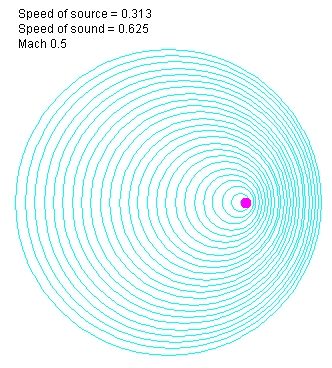
Где-то мы ее видели, не правда ли? Итак, эквипотенциальные поверхности, «замороженные» относительно источника, в этом случае будут выглядеть точно так же, как и «мгновенный снимок» волн, распространяющихся от источника со скоростью  с.

Обратите внимание еще раз - весь смысл этого уравнения для  g  заключается в том, что  g  выражается через координаты источника. Потому что  x - vt  в этом уравнении - это именно расстояние от источника (по оси  х;  значения по осям  y  и  z  у СОИ и СОПС совпадают) в момент времени  t  до любой точки, где мы хотим определить значение  g.

В обеих системах отсчета, время течет одинаково; никакого «сжатия» по направлению движения нет и в помине. Все детали процесса распространения волн выглядят абсолютно одинаково и описываются одинаковыми формулами (с единственной разницей:  u  ↔  x – vt).

Теперь посмотрим внимательнее на множитель  f  в выражении для  g:

g = f / r’

Чему он равен? Точнее, зависит ли он от расстояния  r',  от скорости источника  v,  от чего-то еще? Если  f  не зависит от  x, y, z  и  v,  а также не зависит от времени (для простоты, я не рассматривал зависимость от времени, в частности, потому, что аналогичный множитель для потенциала электрического поля от времени не зависит), то выражение для  g  в момент времени  t  будет таким, как записано выше.

Но предположим, что  f  как раз зависит от  r'  и  v.  Допустим,  мы имеем такую зависимость:

f = f₀ / (1 – r’∙v / (r’ c))

или, что то же самое:

f = f₀ / (1 – β cos α)

где  α – угол между векторами  r’  и  v.

Полная зависимость  g  от расстояния  r’  и скорости  v  станет:

g = f₀ / (r’ – r’∙v / c)

Нам, опять же, даже в СОПС неудобно записывать выражение для  g  относительно запаздывающих координат источника (r' - это вектор от той точки, где был источник в момент излучения волны, до точки измерения  g).  Гораздо удобнее выразить  g  в любой точке в момент времени  t  (то есть в настоящий момент) через координаты источника в этот же момент времени  t.  Путем, опять же, простых геометрических манипуляций мы легко получим:

r’ – r’∙v / c = (u² + (1 – β²) (y² + z²))^½

Это выражение даже несколько проще, чем просто для  r'.  Итак, в координатах источника, мы получили

g = f₀ / (u² + (1 – β²) (y² + z²))^½

При фиксированных значениях  g  (g = g₁,  g = g₂,  g = g₃,  g = g₄,  и т.д.), это уравнение описывает эквипотенциальные поверхности, «замороженные» относительно источника. Сплющенные по координате  u  в  1 / (1 – β²)^½  раз, причем, обратите внимание, симметричные спереди и сзади: 
 

 
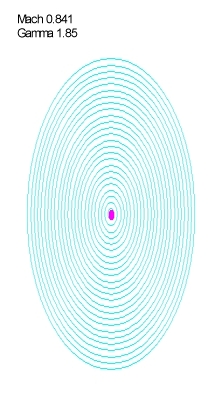
Еще раз – сплющенные по координате  u, в системе отсчета источника. Наблюдатель в СОИ будет видеть, что эквипотенциальные поверхности при движении источника сжимаются в гамма раз по направлению движения. Этот наблюдатель отнюдь не будет считать, что никакого сжатия эквипотенциальных поверхностей нет, что все происходит так, как будто источник покоится (тогда выражение для  g  было бы  g = f₀ / (u² + y² + z²)^½). Он увидит сжатие точно так же, как и наблюдатель, покоящийся относительно среды.

Для этого, второго, наблюдателя из СОПС, выражение для  g  будет выглядеть так:

g = f₀ / ((x – vt)² + (1 – β²) (y² + z²))^½

То есть мы опять произвели замену переменных при помощи преобразования Галилея  u = x – vt.  Оба наблюдателя видят абсолютно одинаковую картину распространения волн и сжатия эквипотенциальных поверхностей.

И еще раз обратите внимание - весь смысл этого уравнения для  g  (хотя оно и записано в СОПС) заключается в том, что  g  выражается через координаты источника. Потому что  x - vt  в этом уравнении - это именно расстояние от источника (по оси  х;  значения  y  и  z  в СОИ и СОПС совпадают) в момент времени  t  до любой точки, где мы хотим определить значение  g.  Это голая геометрия - и никакой "физики", которая заставила бы движущееся тело изменить свои размеры. Ничего не изменилось - мы просто выразили координаты источника в СОПС через координаты этого же источника в СОИ.

Я пытался показать, что сам вывод этого уравнения для сжатого по оси движения потенциала происходил при помощи перехода в СОИ, был сделан изначально в координатах источника. Да, можно вывести это же уравнение и без Галилеевского перехода в СОИ, как и сделал Фейнман. Ну и что? Смысл этого уравнения все равно остается тем же самым: это результат решения простой геометрической задачки, а именно - как выразить расстояние  r'  в координатах СОПС через  r  в координатах СОИ. Никакого глубокого физического смысла здесь нет. Только элементарная геометрия – на уровне что, класса шестого?

При этом, сферические фронты волн  g,  невзирая на сжатие (или отсутствие сжатия) "замороженных" эквипотенциальных поверхностей, по-прежнему распространяются со скоростью  с  во все стороны от тех точек, где находился источник в момент их излучения (мысленно представьте, что они двигаются):
 

 
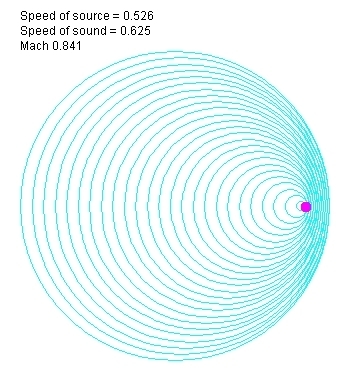
Подчеркну, что так выглядит картина распространения фронтов волн в обеих системах отсчета (точнее, во всех инерциальных СО). В СОПС, фронты волн распространяются по формуле:

(x – vԏ)² + y² + z² = c²(t – ԏ)²

или, для  i-ой единичной волны:

(x – v i dt)² + y² + z² = c² (t – i dt)²

В СОИ фронты волн распространяются так (замена  x = u + vt):

(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²

или

(u + v (t – i dt))² + y² + z² = c² (t – i dt)²

Это уравнение описывает сферические фронты волн, распространяющиеся со скоростью  c  и «сдуваемые» встречным ветром со скоростью  –v.

Обратите внимание, сжатие эквипотенциальных поверхностей произошло по одной-единственной причине: из-за введения дополнительного множителя  1 / (1 – r’∙v / (r’ c)).  Давайте теперь перейдем к этому множителю Лиенара-Вихерта-Доплера (ЛВД).

Не вдаваясь пока в детали, заметим, что этот множитель выводится из самого факта движения источника волн. Он не имеет никакой специфической привязки к электромагнитным волнам и процессам. Если вывод уравнения Лиенара-Вихерта справедлив, то он справедлив для любых волн. В том числе для звуковых. Значит, следуя логике теории относительности, для звуковых волн и их источников тоже надо вводить преобразования Лоренца для координат и времени. При приближении скорости источника к скорости звука, его линейные размеры в направлении движения должны уменьшаться, а время – замедляться. Собственно, именно к необходимости сжатия в направлении движения для звуковых волн и пришел Блохинцев, правда, он почему-то не стал высказываться в пользу замедления времени при приближении источника к скорости звука. Но первый шаг, относительно сжатия по оси  х,  он все же сделал – потому что математика физики заставила его сделать его. Я не смеюсь и не издеваюсь над Блохинцевым, ровно наоборот. Ему хватило научной смелости сделать этот шаг. Благодаря этому, мне легче аргументировать, что все те математические манипуляции, которые обычно делаются при выводе преобразований Лоренца, точно так же применимы ко всем волнам, а не только к электромагнитным, ко всем источникам.

Хм... Как-то я не вполне убежден, что у меня получилось пересказать на пальцах и без формул. Но по крайней мере, их меньше.