Тред №581168

Картины в масле 2

Поставим еще несколько экспериментов с движением объектов в масле. Правда, сейчас влияние гравитации нам не нужно, будет только отвлекать. Можно поставить эксперименты на орбите, в невесомости (когда-нибудь, обязательно).

Итак, космонавт Вася держит в руках дробовик с низкой кучностью (то есть дробь вылетает из него довольно широким пучком). Рядом с ним находится брусок мягкого сливочного масла М₁, неподвижный относительно Васи. Дробовик направлен в сторону этого бруска (по оси  y). С другой стороны бруска, вплотную к нему по оси  х  со скоростью  v₂₁  двигается очень большой брусок масла М₂. В момент времени  t₁, как раз когда бруски поровнялись, Вася стреляет. Дробинки, которые летят под разными углами, проходят сначала брусок М₁ и входят в брусок М₂. Теперь мы не будем пренебрегать сопротивлением масла, так что все дробинки в конце концов остановятся (относительно М₂). В направлении оси  z  (сверху), имеются несколько удаленных наблюдателей (двигающихся с разными скоростями) с телескопами. Что они увидят?

Пусть часть телескопов настроена на брусок М₁. В эти телескопы все наблюдатели увидят, как дробь двигается от дробовика сквозь масло М₁. В момент времени  t₂   дробь достигнет конца бруска М₁ и выйдет из него. Если наблюдатели в этот момент сделают мгновенные снимки системы, то все они увидят следующее:
 

 
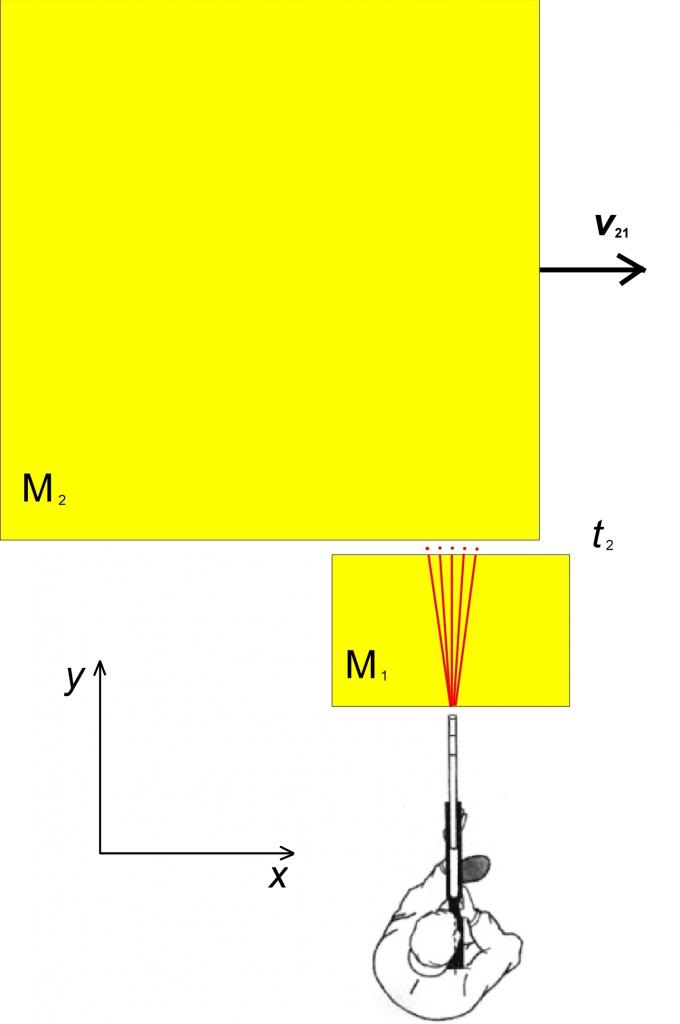
Каждая дробинка оставила трек в масле М₁ – прямую линию (веер красных линий от ствола дробовика). Сами дробинки «висят» в воздухе между М₁ и М₂.

Далее дробинки входят в брусок масла М₂ и продолжают движение уже в нем, пока в момент времени  t₃  не остановятся из-за сопротивления масла. Пусть другая часть телескопов была заранее настроена на брусок М₂. Что увидят наблюдатели в эти телескопы в момент  t₃? Поскольку для них брусок М₂ неподвижно находится в центре поля зрения телескопа, они считают, что это брусок М₁ и стрелок Вася двигаются влево со скоростью  –v₂₁. За время  t₃ – t₂,  которое понадобилось на замедление дроби до полной остановки, брусок М₁ и стрелок успеют сместиться на некоторое расстояние:
 

  
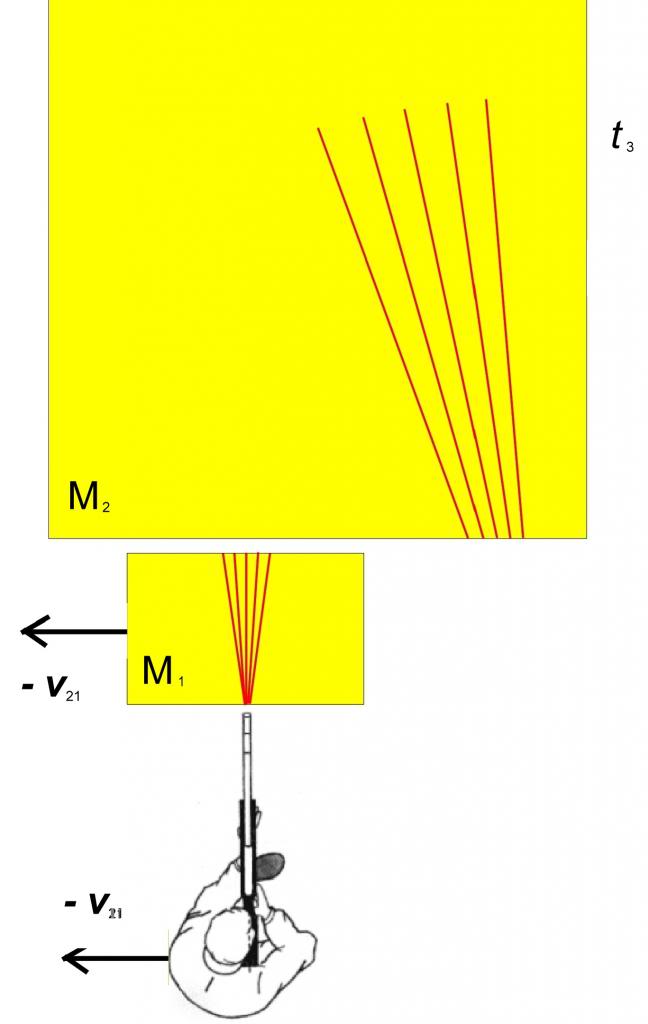
Что здесь важно? Во-первых, при переходе из М₁ в М₂, двигающийся относительно М₁ со скоростью   v₂₁, скорость  per medium  дробинки резко меняется. Пусть скорость дробинки относительно бруска М₁ (с внутренней системой координат X₁Y₁ Z₁) на выходе из М₁ была равна  V₁(V_X₁, V_Y₁, V_Z₁). Тогда при входе дробинки в М₂ ее скорость относительно внутренней системы координат М₂, то есть  X₂Y₂ Z₂,  будет равна

V₂ (V_X₂, V_Y₂, V_Z₂) = V₁(V_X₁, V_Y₁, V_Z₁) –  v₂₁

Это тот самый Принцип Аберрации Движения, о котором я уже упоминал и о котором мы будем еще очень много говорить. Сейчас мы рассматриваем этот принцип в рамках механики, но наиболее важен он для распространения волн и сил. Этот принцип, ни много ни мало, позволит нам построить новую электродинамику. Принципиально отличную от электродинамики Максвелла. При этом, очень простую и наглядную.

Для материальных тел, этот принцип формулируется следующим образом:

Аксиома 9 (Принцип Аберрации Скорости Движения Тел): При переходе из среды 1 в среду 2, двигающуюся относительно среды 1 со скоростью  v₂₁, скорость тела в среде 2 будет равна скорости этого тела в среде 1 минус скорость  v₂₁.

Во-вторых, обратите внимание, треки (следы в масле) дробинок в бруске М₂ (как, впрочем, и в бруске М₁), это прямые линии. Реальные, материальные, объективно существующие прямые линии, подчиняющиеся Аксиоме 8, то есть выглядящие одинаково для всех наблюдателей во всех системах отсчета.

В отличие от треков русики, физику интересуют «воображаемые» траектории дробинок (о том, почему я называю траектории воображаемыми, см. мое предыдущее сообщение) в координатах СО неких наблюдателей, двигающихся с разными скоростями. Скажем, траектории движения дробинок с позиции наблюдателя, находящегося в одной СО с Васей, но расположенного над ним, должны выглядеть вот так:
 

 
Это отнюдь не прямые линии, а кривые, поскольку из-за сопротивления масла дробинки двигались с замедлением, а кроме того, когда они двигались сквозь брусок М₂, на них слева дул «масляный ветер». Собственно, воображаемые траектории будут кривыми во всех СО.

Треки же русики, еще раз, – прямые линии. Их «прямизна» является следствием того факта, что при движении дробинки сквозь брусок масла система отсчета, связанная с этим бруском, является выделенной, поскольку силы, действующие на дробинку полностью определяются именно ее взаимодействием со средой. Конечно, если бы на дробинку действовали дополнительные силы, скажем, сила тяжести или тяга ракетных двигателей, то ее трек был бы совсем не прямым. Но для того мы и выбрали такой упрощенный вариант, чтобы вычленить главное. А главным является то, что важнейшей характеристикой движения тела является именно его движение сквозь среду  (per medium).  Движение же тела относительно некой системы отсчета  (ad aspicientis)  является, в этом смысле, второстепенной характеристикой. Хотя для полного описания движения тела нужны оба вида движения.

Попробую объяснить значение движения тела сквозь среду другими словами. Давайте представим себе, что дробинки у нас живые (как пассажир, который ехал на открытой дрезине сквозь масло). То есть они могут чувствовать, какие силы на них действуют. Или они неживые, но их поверхность утыкана нанодатчиками давления, которые позволяют нам измерить силы, действующие на них со стороны среды. Как дробинки будут «чувствовать» ветер? Очень просто – среда оказывает давление на всю поверхность дробинки; если давление со всех сторон одинаково, ветра нет. Если давление с определенной стороны больше, чем с противоположной, то ветер дует с того направления, где давление максимально.

Если дробинка двигается сквозь среду с какой-то скоростью, то для нее это эквивалентно встречному ветру с той же скоростью, но противоположного направления. С точки зрения дробинки, откуда, с какого направления на нее дует встречный ветер, когда она двигается сквозь среду М₁ по оси y? Ветер дует на нее также по оси  y, но в противоположном направлении. Элементарно, Ватсон. Теперь дробинка входит в среду М₂. Откуда ветер дует теперь? А как раз с направления, противоположного вектору ее скорости относительно внутренней системы координат М₂:

V₂(V_X₂, V_Y₂, V_Z₂) = V₁(V_X₁, V_Y₁, V_Z₁) –  v₂₁

То есть дробинка «чувствует» встречный ветер именно с того направления, откуда он должен дуть в среде отсчета бруска М₂. Но «чувства» дробинки – это лирика. А какая (грубая, материальная) сила действует на дробинку со стороны среды М₂? Сила сопротивления, то есть. В каком направлении?

В том же самом, что и встречный ветер. Поскольку градиент давления – это сила, а направление, откуда на дробинку дует встречный ветер, мы определяем тоже как градиент давления. А согласно физике, сила, между прочим, инвариантна относительно преобразований Галилея – вектор силы одинаков в любой инерциальной системе отсчета. Хотя преобразования Галилея и инерциальные системы отсчета не играют в русике такую же роль, как в физике, русика здесь согласна с физикой.