Тред №596774

д) Луч 5

Напомню, что луч 1 – поперечный. Лучи 2, 3 и 4 падают на элемент М₂ хоть и под углом, но «вдогонку»: он удаляется от источника. Лучи 5 и 6 «встречные» – элемент М₂ приближается к источнику.

Пусть фронт волны падает на границу раздела М₁ и М₂ под углом  ψ, который для луча 5 больше 90° (угол WBC). В момент  t₀  фронт касается границы в точке А / A'. Через промежуток времени  ∆t,  элемент М₂ сдвинется вправо на расстояние  v∆t,  в том числе сдвинется точка A’, а фронт волны сдвинется влево-вверх на расстояние  c∆t  (вектор СВ). Согласно Аксиоме 10, точка A' станет источником вторичной сферической волны радиуса  c∆t,  распространяющейся в элементе М₂. Чтобы получить фронт волны в элементе М₂, мы должны соединить точки B и D; соответствующий луч перпендикулярен этому фронту.
 

 
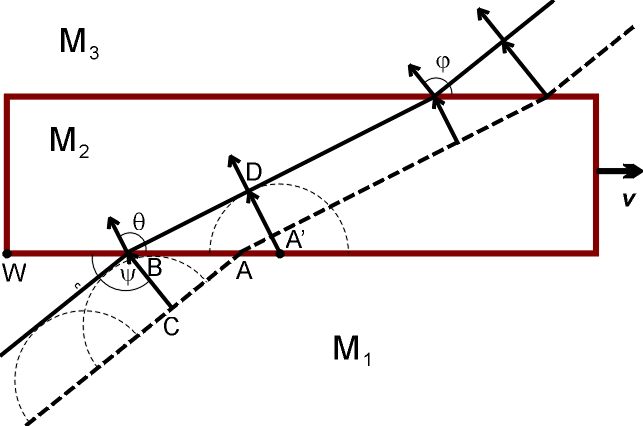
Из рисунка видно, что луч 5, так же как и луч 2, отклоняется в том же направлении, в котором двигается элемент М₂. Все формулы для углов  ψ, θ, φ  и длин волн  λ₁, λ₂, λ₃,  написанные выше для луча 2, собственно, справедливы и для луча 5. При этом

0° <  ψ  < 180°

е) Луч 6

Луч 6 отличается от луча 5 тем, что он направлен почти по касательной к границе раздела М₁ и М₂, то есть угол  ψ  почти равен 180°:
 

 
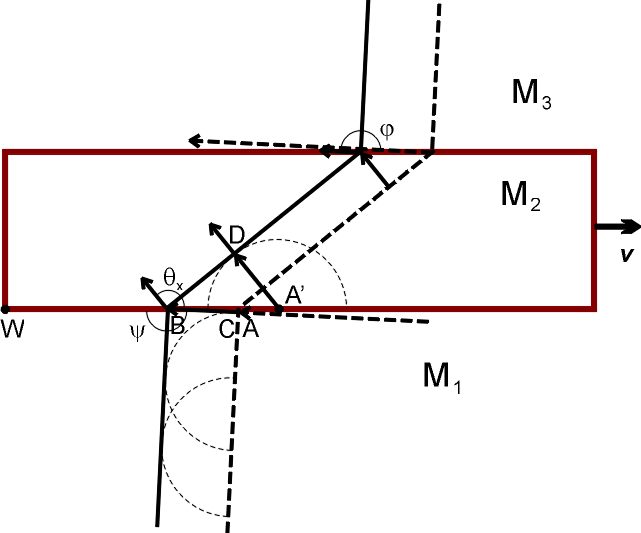
Подставив  ψ = 180°  в уравнение  cosθ = 1/(1/cosψ – v/c), мы получим критический, или максимальный, угол  θₓ:

cosθₓ = – 1/(1 + v/c)

При малых скоростях элемента М₂, то есть при  v ≪ c,  угол  θₓ  будет стремиться к 135°.