Тред №608832

Откуда берутся 100 км.

Читаем http://www.astronet.ru/db/msg/1201995

2. Поле тяготения невращающейся черной дыры

Движение тел в поле тяготения Шварцшильда обладает рядом особенностей. В теории Ньютона движение по окружности вокруг тяготеющего центра возможно на любом расстоянии R от него. В теории Эйнштейна это не так. Чем ближе к Ч.д., тем больше скорость кругового движения. На окружности с R=1,5 r_g скорость движения достигает световой. Ближе к Ч.д. движение по окружности, очевидно, вообще невозможно. В действительности же движение по окружности становится неустойчивым на значительно больших расстояниях, а именно: начиная с R=3 r_g, когда скорость движения составляет всего половину световой. Только на расстояниях, превышающих 3r_g, возможно устойчивое круговое движение. На пределе устойчивости круговых орбит энергия связи частицы \Delta\varepsilon=0,06 mc², где m - масса частицы.

Особый интерес представляет возможность гравитац. захвата черной дырой тел, прилетающих из бесконечности к тяготеющей массе, описывает около нее параболу или гиперболу и (если не испытывает соударения с тяготеющей массой) снова улетает в бесконечность. Гравитац. захват в этой задаче невозможен.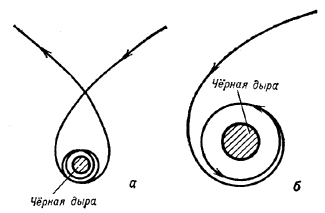


Рис. 1.
Иначе обстоит дело в поле тяготения Ч.д. Конечно, если тело движется на больших расстояниях от Ч.д. (R>r_g), где поле тяготения уже слабо и справедлива с большой точностью теория Ньютона, то траектория движения почти точно совпадает с параболой или гиперболой. В достаточной близости от Ч.д. траектория резко отличается от ньютоновской. Так, если скорость тела вдали от Ч.д. много меньшн световой и траектория его движения подходит близко к окружности с R=2 r_g, то тело совершит много оборотов вокруг Ч.д., прежде чем снова улетит в космос (рис. 1, а).

Наконец, если тело подойдет вплотную к указанной окружности, то его орбита будет неограниченно навиватсья на окружность. Тело окажется гравитационно захваченным Ч.д. и никогда снова не улетит в космос (рис. 1, б). Если же тело подлетит еще ближе к Ч.д., то после неск. оборотов или даже не успев сделать ни одного оборота, оно упадет в Ч.д.