Жизнь, Разум, Человек, Религия и Наука
149,896
565
|
Yuri Rus ( Слушатель ) |
| 02 сен 2013 15:16:21 |
Тред №611238
новая дискуссия Дискуссия 256
Эксперимент Майкельсона-Морли
Видите ли, в чем дело. Сама постановка экспериментов Миллера (см. здесь), так же как и экспериментов Майкельсона-Морли, Ives–Stilwell и Kennedy–Thorndike, неверна. Неверна и их интерпретация. Причем ошибок там много. Некоторые из них можно было заметить и в рамках физики (еще в XIX веке), другие – только в рамках русики.
Полный разбор всех ошибок ЭМ-М занял бы слишком много времени; кроме того, для этого нам понадобилось бы сначала разобраться с аберрацией света (в частности, с аберрацией преломления). К сожалению, я никак не доберусь до аберрации света (а она, как я подчеркивал, происходит совсем иначе, чем аберрация звука). Слишком много у меня сейчас проблем.
Но нам совсем не обязательно делать полный разбор всех ошибок ЭМ-М прямо сейчас. Здесь как в известном историческом анекдоте про Наполеона: однажды он потребовал объяснений, почему комендант некой крепости не дал в честь его прибытия пушечный салют. Комендант сказал: «У меня есть 21 причина, почему я не мог этого сделать. Первая – нет пороха…» «Достаточно», – прервал его Наполеон.
Так что давайте отложим аберрацию преломления света на потом, а сейчас ограничимся анализом аберрации отражения света от 3 зеркал ЭМ-М. Мы увидим, что меняются как углы, под которыми лучи света отражаются от движущихся зеркал, так и длины волн отраженного света. Этого «достаточно», чтобы понять, что общепринятая в течение последних примерно 125 лет интерпретация ЭМ-М неверна – потому что она слишком упрощенная.
Цитата из статьи Майкельсона и Морли 1887 г. (та самая общепринятая интерпретация):
Перевод на русский:
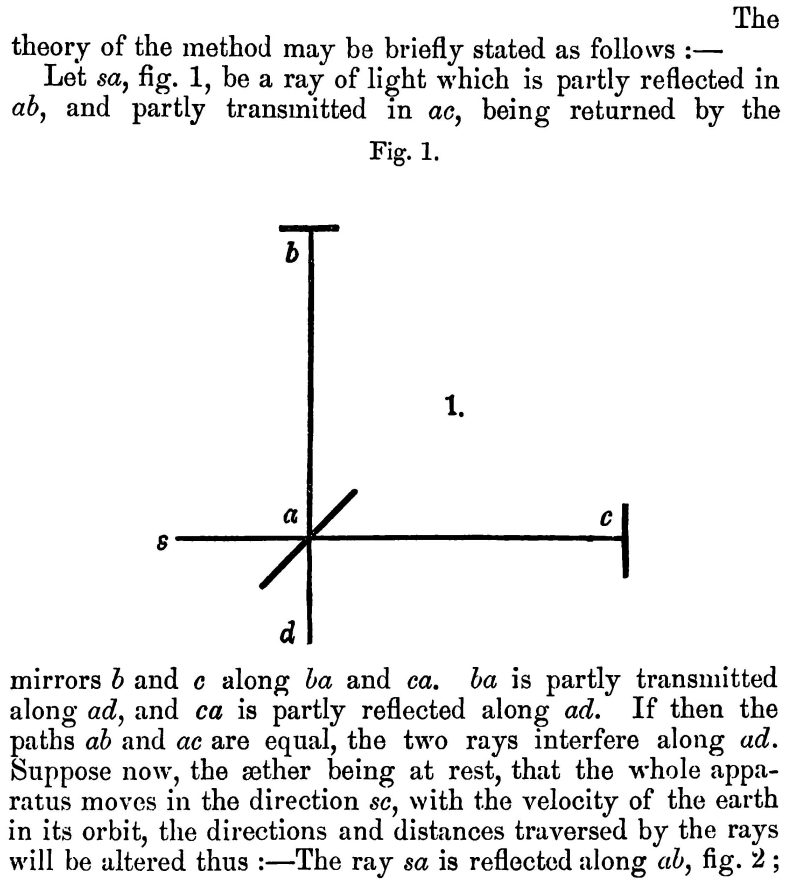
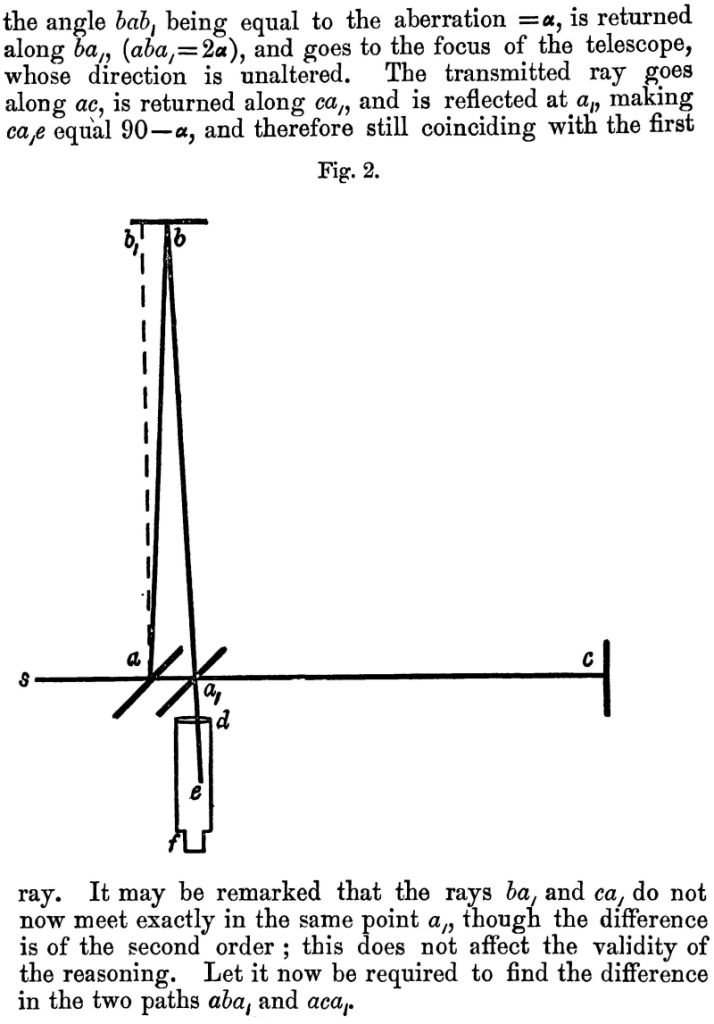
Теорию метода можно вкратце сформулировать следующим образом. Пусть sa рис. 1 – это луч света, который частично отражается в ab, а частично проходит через стекло в ас, возвращаясь при помощи зеркал b и с вдоль ba и ca. ba частично проходит через стекло вдоль ad, а ac частично отражается вдоль ad. Если отрезки аb и ас равны, то эти два луча интерферируют вдоль ad. Предположим теперь, что эфир находится в покое и что весь аппарат движется в направлении sc со скоростью Земли по ее орбите, тогда направления и расстояния, проходимые лучами, будут меняться таким образом: луч sa отражается вдоль ab рис. 2 (угол bab₁ равен аберрации α), возвращается вдоль ba₁ (aba₁ = 2α) и идет в фокус телескопа, направление которого остается неизменным. Луч, прошедший сквозь стекло, идет вдоль ас, возвращается вдоль ca, и отражается в a₁, делая ca₁e равным 90 – α и, таким образом, вновь совпадая с первым лучом. Следует отметить, что лучи ba₁ и ca₁ не встречаются точно в одной и той же точке a₁, хотя разница здесь второго порядка; это не влияет на справедливость вывода. Давайте теперь найдем разницу двух путей aba₁ и аса₁.
В самом низу страницы 7 данной ветки я приводил цитату из книги М. Борна “Эйнштейновская Теория Относительности”, М., Мир, 1972, стр. 209-214, где как раз имеется вывод времен, которые тратят продольный и поперечный лучи на прохождение этих путей. Это – суть ЭМ-М и это основа теории относительности.
Что же здесь неверно? Казалось бы, логика ЭМ-М обсуждалась столько раз, что для ошибки тут места просто нет (с чем, впрочем, не согласятся альты). Неверно здесь то, что интерферометр Майкельсона – это не секундомер и не линейка. Он не меряет ни время, затраченное лучами, ни пройденное ими расстояние. Интерферометр – это, пардон за тавтологию, устройство, которое имеет дело с волнами и их длинами. Поэтому нам совершенно недостаточно знать, сколько времени (теоретически) затратят лучи света на путешествия между зеркалами a, b и c. Мы должны еще определить, как при этих отражениях изменятся длины волн этого света и углы, под которыми лучи попадают в детектор. А они изменятся (surprise!). И насколько мне известно, за все 125 лет с момента публикации статьи Майкельсона-Морли, вопрос, что же происходит с длинами волн и углами отраженных лучей, никто не анализировал.
Этим мы сейчас и займемся. Всё, что нам для этого анализа нужно, – это принцип Гюйгенса (даже не в формулировке Аксиомы 10 русики, а в более простой формулировке физики). Будем обозначать зеркала и прочее так же, как в оригинальной статье Майкельсона-Морли.
Пусть в момент времени t₀ на полупрозрачное зеркало a, расположенное под углом 45 градусов к лучам света, падают два последовательных волновых фронта, расстояние между которыми равно λ₁. Фронт 1 касается зеркала в точке Е, фронт 2 – в точке А. Фронты падающих волн обозначены светло-синими линиями, падающие лучи – светло-зелеными стрелками.
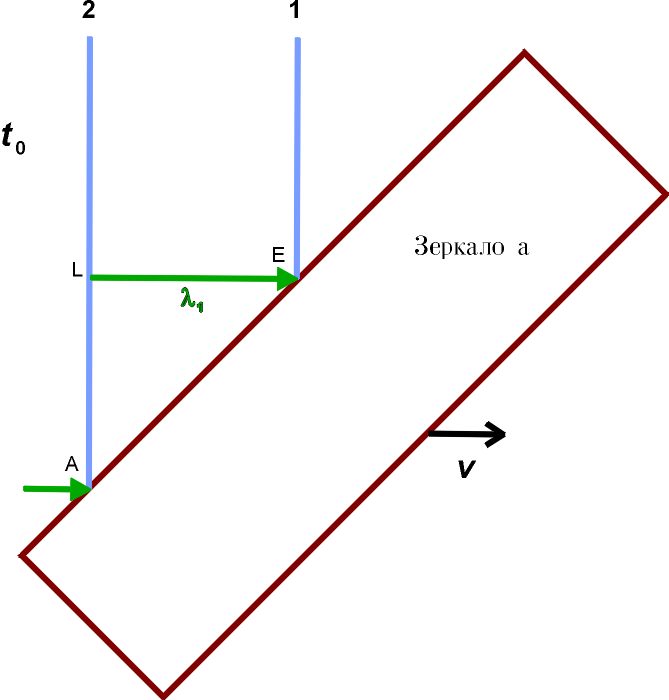
Через промежуток времени Δt, фронт волны 2 займет место фронта волны 1 (то есть λ₁ = c Δt). За это время, зеркало а сдвинется вправо на расстояние λ₁ v/c. Согласно Принципу Гюйгенса, точки A и E станут источниками вторичных сферических волн, распространяющихся в воздухе. Радиус этих волн будет равен λ₁. Чтобы получить фронт отраженной волны 1’ (темно-синяя линия), нам надо провести касательную линию между точкой H, в которой падающий фронт 1 касается зеркала в момент t₀ + Δt, и окружностью радиуса λ₁ с центром в точке Е. Аналогично, чтобы получить фронт отраженной волны 2’ (темно-синяя линия), надо провести касательную линию между точкой В, в которой падающий фронт 2 касается зеркала в момент t₀ + Δt, и окружностью радиуса λ₁ с центром в точке А. Соответствующие лучи (темно-зеленые стрелки) перпендикулярны этим фронтам.
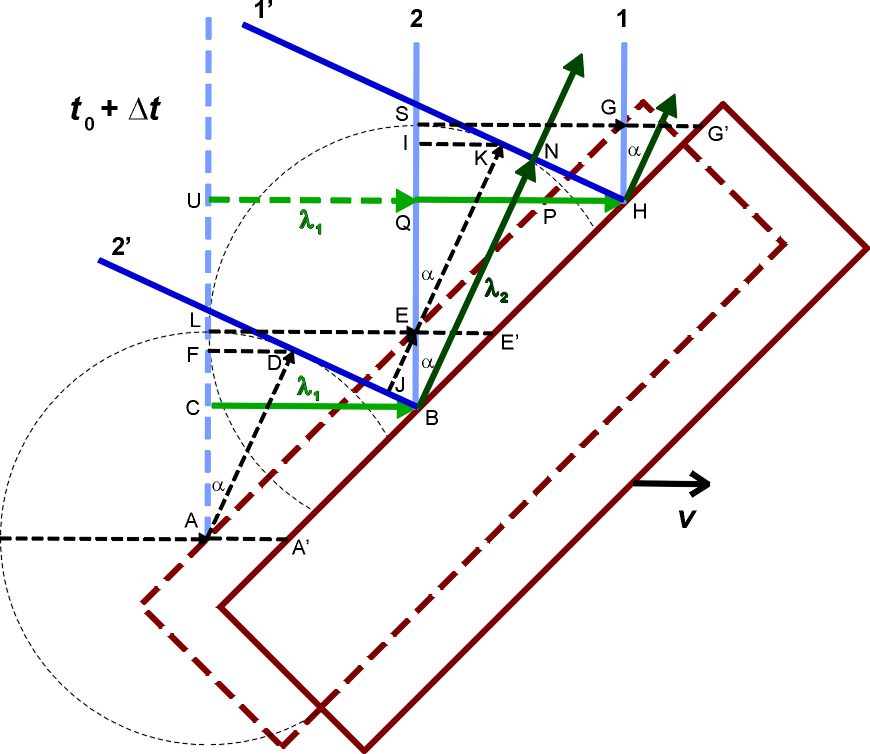
Как и у Майкельсона-Морли, обозначим угол аберрации отражения α. При помощи несколько громоздких геометрических манипуляций (долго писать, поэтому пока их не привожу; но если появятся вопросы, могу выложить доказательство), мы можем получить следующие уравнения для угла аберрации α луча, отраженного от двигающегося зеркала, расположенного под углом 45 градусов:
sin α = (1 – (1 – β)²) / (1 + (1 – β)²) = (β – β²/2) / (1 – β + β²/2)
cos α = 2 (1 – β) / (1 + (1 – β)²) = (1 – β) / (1 – β + β²/2)
Здесь β = v/c, как общепринято в физике.
Обратите внимание, что длина отраженной волны λ₂ больше длины падающей волны λ₁. Мы легко можем получить соотношение между ними:
λ₂ = |EK| + |JE| = λ₁ + λ₁ β cos α = λ₁ (2 – β²) / (1 + (1 – β)²) = (1 – β²/2) / (1 – β + β²/2)
На что еще стоит обратить внимание: если зеркало а расположено действительно под углом 45 градусов, то отраженный луч будет немного «забегать вперед». Что имеется в виду: за время Δt, зеркало а сместится на расстояние λ₁ β. Скажем, точка Е сместится в точку Е': |EE’| = λ₁ β. За это же время, отраженный луч из той же точки Е сместится в точку K. Так вот, расстояние |IK| больше расстояния |EE’|, то есть отраженный луч будет двигаться не строго напротив той точки на зеркале а, от которой он отразился, а чуть-чуть впереди ее. Это очевидно из уравнения для sin α:
|IK| = λ₁ sin α = λ₁ (β – β²/2) / (1 – β + β²/2)
Скажем, для β = 0.5, |EE’| = 0.5 λ₁, а |IK| = 0.6 λ₁.
При β ≪ 1, |IK| ≈ λ₁ β (1 + β), тогда как |EE’| = λ₁ β.
Нет, все-таки придется мне дать полный вывод уравнения для sin α. Но чуть позже.
Затем эти лучи, отраженные от зеркала а, доходят до зеркала b и отражаются от него. Если зеркало b расположено как показано на рисунке у Майкельсона, то есть параллельно вектору движения интерферометра относительно Солнца (или вообще относительно эфира), то никакой аберрации при отражении от зеркала b не будет. На место одних точек зеркала все время становятся другие точки, так что ни угол, ни длина волны отраженного луча не изменятся.
Далее, для простоты, будем полагать, что лучи, отраженные от зеркала b, не проходят сквозь полупрозрачное зеркало а (для этого нам пришлось бы анализировать аберрацию преломления света, а мы до этого еще не дошли), а просто проходят сквозь щель в зеркале а. Обойдемся пока упрощенным вариантом ЭМ-М – для доказательства ошибочности общепринятой интерпретации этого эксперимента, нам «достаточно» и анализа аберрации отражения.
Пусть второй луч, аналогично, не проходит сквозь полупрозрачное зеркало a, как у Майкельсона-Морли, а всего лишь проходит сквозь щель в нем (без преломления) и следует далее до зеркала c. Рассмотрим опять два последовательных волновых фронта, расстояние между которыми равно λ₁. После отражения от зеркала с, длина отраженной волны станет равна
λ₃ = λ₁ (1 + β) / (1 – β)
Это просто эффект Доплера для отражения света от двигающегося объекта; на этом основано применение радаров для определения, скажем, скоростей автомобилей.
Затем эти фронты возвращаются к зеркалу а и отражаются от него вниз – опять с аберрацией. Сейчас я прервусь, завтра-послезавтра сделаю картинки и напишу формулы для этого отражения.
Но думаю, сказанного уже достаточно, чтобы показать, что интерферометр Майкельсона измерял не совсем то, что предполагали Майкельсон и Морли, а за ними и все их последователи. И лучи были направлены не так, и длины волн этих лучей были не те. Нет, ребята, всё не так, всё не так, как надо.
Видите ли, в чем дело. Сама постановка экспериментов Миллера (см. здесь), так же как и экспериментов Майкельсона-Морли, Ives–Stilwell и Kennedy–Thorndike, неверна. Неверна и их интерпретация. Причем ошибок там много. Некоторые из них можно было заметить и в рамках физики (еще в XIX веке), другие – только в рамках русики.
Полный разбор всех ошибок ЭМ-М занял бы слишком много времени; кроме того, для этого нам понадобилось бы сначала разобраться с аберрацией света (в частности, с аберрацией преломления). К сожалению, я никак не доберусь до аберрации света (а она, как я подчеркивал, происходит совсем иначе, чем аберрация звука). Слишком много у меня сейчас проблем.
Но нам совсем не обязательно делать полный разбор всех ошибок ЭМ-М прямо сейчас. Здесь как в известном историческом анекдоте про Наполеона: однажды он потребовал объяснений, почему комендант некой крепости не дал в честь его прибытия пушечный салют. Комендант сказал: «У меня есть 21 причина, почему я не мог этого сделать. Первая – нет пороха…» «Достаточно», – прервал его Наполеон.
Так что давайте отложим аберрацию преломления света на потом, а сейчас ограничимся анализом аберрации отражения света от 3 зеркал ЭМ-М. Мы увидим, что меняются как углы, под которыми лучи света отражаются от движущихся зеркал, так и длины волн отраженного света. Этого «достаточно», чтобы понять, что общепринятая в течение последних примерно 125 лет интерпретация ЭМ-М неверна – потому что она слишком упрощенная.
Цитата из статьи Майкельсона и Морли 1887 г. (та самая общепринятая интерпретация):
Перевод на русский:
Теорию метода можно вкратце сформулировать следующим образом. Пусть sa рис. 1 – это луч света, который частично отражается в ab, а частично проходит через стекло в ас, возвращаясь при помощи зеркал b и с вдоль ba и ca. ba частично проходит через стекло вдоль ad, а ac частично отражается вдоль ad. Если отрезки аb и ас равны, то эти два луча интерферируют вдоль ad. Предположим теперь, что эфир находится в покое и что весь аппарат движется в направлении sc со скоростью Земли по ее орбите, тогда направления и расстояния, проходимые лучами, будут меняться таким образом: луч sa отражается вдоль ab рис. 2 (угол bab₁ равен аберрации α), возвращается вдоль ba₁ (aba₁ = 2α) и идет в фокус телескопа, направление которого остается неизменным. Луч, прошедший сквозь стекло, идет вдоль ас, возвращается вдоль ca, и отражается в a₁, делая ca₁e равным 90 – α и, таким образом, вновь совпадая с первым лучом. Следует отметить, что лучи ba₁ и ca₁ не встречаются точно в одной и той же точке a₁, хотя разница здесь второго порядка; это не влияет на справедливость вывода. Давайте теперь найдем разницу двух путей aba₁ и аса₁.
В самом низу страницы 7 данной ветки я приводил цитату из книги М. Борна “Эйнштейновская Теория Относительности”, М., Мир, 1972, стр. 209-214, где как раз имеется вывод времен, которые тратят продольный и поперечный лучи на прохождение этих путей. Это – суть ЭМ-М и это основа теории относительности.
Что же здесь неверно? Казалось бы, логика ЭМ-М обсуждалась столько раз, что для ошибки тут места просто нет (с чем, впрочем, не согласятся альты). Неверно здесь то, что интерферометр Майкельсона – это не секундомер и не линейка. Он не меряет ни время, затраченное лучами, ни пройденное ими расстояние. Интерферометр – это, пардон за тавтологию, устройство, которое имеет дело с волнами и их длинами. Поэтому нам совершенно недостаточно знать, сколько времени (теоретически) затратят лучи света на путешествия между зеркалами a, b и c. Мы должны еще определить, как при этих отражениях изменятся длины волн этого света и углы, под которыми лучи попадают в детектор. А они изменятся (surprise!). И насколько мне известно, за все 125 лет с момента публикации статьи Майкельсона-Морли, вопрос, что же происходит с длинами волн и углами отраженных лучей, никто не анализировал.
Этим мы сейчас и займемся. Всё, что нам для этого анализа нужно, – это принцип Гюйгенса (даже не в формулировке Аксиомы 10 русики, а в более простой формулировке физики). Будем обозначать зеркала и прочее так же, как в оригинальной статье Майкельсона-Морли.
Пусть в момент времени t₀ на полупрозрачное зеркало a, расположенное под углом 45 градусов к лучам света, падают два последовательных волновых фронта, расстояние между которыми равно λ₁. Фронт 1 касается зеркала в точке Е, фронт 2 – в точке А. Фронты падающих волн обозначены светло-синими линиями, падающие лучи – светло-зелеными стрелками.
Через промежуток времени Δt, фронт волны 2 займет место фронта волны 1 (то есть λ₁ = c Δt). За это время, зеркало а сдвинется вправо на расстояние λ₁ v/c. Согласно Принципу Гюйгенса, точки A и E станут источниками вторичных сферических волн, распространяющихся в воздухе. Радиус этих волн будет равен λ₁. Чтобы получить фронт отраженной волны 1’ (темно-синяя линия), нам надо провести касательную линию между точкой H, в которой падающий фронт 1 касается зеркала в момент t₀ + Δt, и окружностью радиуса λ₁ с центром в точке Е. Аналогично, чтобы получить фронт отраженной волны 2’ (темно-синяя линия), надо провести касательную линию между точкой В, в которой падающий фронт 2 касается зеркала в момент t₀ + Δt, и окружностью радиуса λ₁ с центром в точке А. Соответствующие лучи (темно-зеленые стрелки) перпендикулярны этим фронтам.
Как и у Майкельсона-Морли, обозначим угол аберрации отражения α. При помощи несколько громоздких геометрических манипуляций (долго писать, поэтому пока их не привожу; но если появятся вопросы, могу выложить доказательство), мы можем получить следующие уравнения для угла аберрации α луча, отраженного от двигающегося зеркала, расположенного под углом 45 градусов:
sin α = (1 – (1 – β)²) / (1 + (1 – β)²) = (β – β²/2) / (1 – β + β²/2)
cos α = 2 (1 – β) / (1 + (1 – β)²) = (1 – β) / (1 – β + β²/2)
Здесь β = v/c, как общепринято в физике.
Обратите внимание, что длина отраженной волны λ₂ больше длины падающей волны λ₁. Мы легко можем получить соотношение между ними:
λ₂ = |EK| + |JE| = λ₁ + λ₁ β cos α = λ₁ (2 – β²) / (1 + (1 – β)²) = (1 – β²/2) / (1 – β + β²/2)
На что еще стоит обратить внимание: если зеркало а расположено действительно под углом 45 градусов, то отраженный луч будет немного «забегать вперед». Что имеется в виду: за время Δt, зеркало а сместится на расстояние λ₁ β. Скажем, точка Е сместится в точку Е': |EE’| = λ₁ β. За это же время, отраженный луч из той же точки Е сместится в точку K. Так вот, расстояние |IK| больше расстояния |EE’|, то есть отраженный луч будет двигаться не строго напротив той точки на зеркале а, от которой он отразился, а чуть-чуть впереди ее. Это очевидно из уравнения для sin α:
|IK| = λ₁ sin α = λ₁ (β – β²/2) / (1 – β + β²/2)
Скажем, для β = 0.5, |EE’| = 0.5 λ₁, а |IK| = 0.6 λ₁.
При β ≪ 1, |IK| ≈ λ₁ β (1 + β), тогда как |EE’| = λ₁ β.
Нет, все-таки придется мне дать полный вывод уравнения для sin α. Но чуть позже.
Затем эти лучи, отраженные от зеркала а, доходят до зеркала b и отражаются от него. Если зеркало b расположено как показано на рисунке у Майкельсона, то есть параллельно вектору движения интерферометра относительно Солнца (или вообще относительно эфира), то никакой аберрации при отражении от зеркала b не будет. На место одних точек зеркала все время становятся другие точки, так что ни угол, ни длина волны отраженного луча не изменятся.
Далее, для простоты, будем полагать, что лучи, отраженные от зеркала b, не проходят сквозь полупрозрачное зеркало а (для этого нам пришлось бы анализировать аберрацию преломления света, а мы до этого еще не дошли), а просто проходят сквозь щель в зеркале а. Обойдемся пока упрощенным вариантом ЭМ-М – для доказательства ошибочности общепринятой интерпретации этого эксперимента, нам «достаточно» и анализа аберрации отражения.
Пусть второй луч, аналогично, не проходит сквозь полупрозрачное зеркало a, как у Майкельсона-Морли, а всего лишь проходит сквозь щель в нем (без преломления) и следует далее до зеркала c. Рассмотрим опять два последовательных волновых фронта, расстояние между которыми равно λ₁. После отражения от зеркала с, длина отраженной волны станет равна
λ₃ = λ₁ (1 + β) / (1 – β)
Это просто эффект Доплера для отражения света от двигающегося объекта; на этом основано применение радаров для определения, скажем, скоростей автомобилей.
Затем эти фронты возвращаются к зеркалу а и отражаются от него вниз – опять с аберрацией. Сейчас я прервусь, завтра-послезавтра сделаю картинки и напишу формулы для этого отражения.
Но думаю, сказанного уже достаточно, чтобы показать, что интерферометр Майкельсона измерял не совсем то, что предполагали Майкельсон и Морли, а за ними и все их последователи. И лучи были направлены не так, и длины волн этих лучей были не те. Нет, ребята, всё не так, всё не так, как надо.
Отредактировано: Yuri Rus - 06 дек 2019 19:21:22
ОТВЕТЫ (10)
|
существо с антитентуры ( Слушатель ) |
| 11 сен 2013 19:23:04 |
Цитата: Yuri Rus от 02.09.2013 15:16:21
Ещё как анализировал. В 1958 году Седархольм пытался повторить эксперимент Майкельсона-Морли, но начал измерять как раз доплеровский эффект изменения частот, на чём и погорел.
Вот в этой книге вся эта история довольно подробно разобрана.
http://ether-wind.narod.ru/Atsukovsky_Ether_2011/Atsukovsky_Ether_2011.pdf
|
|
Yuri Rus ( Слушатель ) |
| 12 сен 2013 03:48:27 |
1. Я имел в виду - никто не анализировал так, как это делаю я (в частности, используя принцип Гюйгенса).
2. В 1958 и 1959 гг. Седархольм и соавторы НЕ пытались повторить эксперимент Майкельсона-Морли. Они поставили совершенно независимые от ЭМ-М эксперименты, где, по их утверждениям, они пытались зарегистрировать эффект движения Земли в эфире первого порядка (а не второго порядка, как в ЭМ-М). Два мазера были направлены друг навстречу другу и за счет доплеровского эффекта ожидались биения. Почему - непонятно, ведь и оба мазера и детектор двигались с одинаковой скоростью относительно эфира. В статье нет даже схемы эксперимента, взаимного расположения мазеров, детектора, детального объяснения того, что должно получиться согласно теории эфира (какой, кстати, теории? их много).
Там есть ссылка на более раннюю работу Møller, C., Nuovo Cimento, 6, Supp., 381-398 (1957), где, насколько можно понять, как раз и была предложена идея этого эксперимента и детальное обоснование ожидаемых результатов. Я нашел эту статью на сайте Springer - http://link.springer…BF02724794. Но скачать, к сожалению, не могу, у меня нет бесплатного университетского доступа к статьям. Если кто-то, у кого есть такой доступ, может прислать статью мне на rus-yuri@yandex.ru, буду благодарен.
|
|
существо с антитентуры ( Слушатель ) |
| 14 сен 2013 14:51:24 |
Цитата: Yuri Rus от 12.09.2013 03:48:27
Ну это понятно. У них и установка была совершенно другая, не имеющая ничего общего с интерферометром. Я имел ввиду, что они так же пытались поймать следы эфира. Но неудачно.
Попробую задать вопрос в этой ветке, если автор не против. Хотел спросить на "как оно тикает", но там наверно сразу забанят за "лженауку"
, а мне всё-таки хотелось бы получить аргументированный ответ.Я тут немного попытался разобраться в вопросах эфирной теории, в частности Ацюковского. Уж очень на многие непонятные для меня вопросы она давала ответы буквально на пальцах, и объясняла те необъяснимые наукой эффекты, с которыми приходилось сталкиваться в жизни. И решил поискать нормальный разбор и опровержение её в сети. Но не нашёл.
Всё, что нашёл, так это пустое словоблудие, противоречащее себе же, а так же придирки к отдельным словам и положениям, не затрагивающим основы. Короче опровержение ещё более неубедительно, чем сама теория. Даже читал переписку каких-то физтехов, так они там сами переругались, но так и не пришли к общему мнению 
Ацюковский сам говорил в каком-то интервью, что опровергнуть его теорию невозможно, неужели он прав? Как вы считаете, есть ли у эфирной теории шанс на развитие? Простое приклеивание ярлыков от господ учёных "лженаука" без объяснения причин что-то не очень устраивает.
|
Свой ( Слушатель ) |
| 14 сен 2013 15:46:30 |
Расслабьтесь. Очень похожий вопрос, пользуясь служебным положением, я задал в Петербургском союзе ученых. На что мне доверительно ответили, что они и сами могут сходу предложить еще полтора десятка "неопровержимых альтернативных теорий". Но пока наблюдаемые явления и прикладные разработки вписываются в ОТО -- на разбор "альтернативки" никто тупо не желает тратить времени.
Так что опровержений -- не будет.
|
|
существо с антитентуры ( Слушатель ) |
| 14 сен 2013 16:10:44 |
Цитата: Свой от 14.09.2013 15:46:30
Спасибо, я что-то подобное и предполагал. Но в принципе я и не искал опровержение "официальное". Ясно, что учёные дяди до такого не опустятся. Мне вполне достаточно было и любительского, просто аргументированного, но даже этого мне не попадалось. А вопрос на самом деле очень непростой, имеет ли смысл тратить своё время и силы на более глубокое изучение и развитие этого направления. Можно конечно просто отмахнуться, но, а вдруг
|
|
expentel ( Слушатель ) |
| 15 сен 2013 16:29:43 |
А почему нет? Автор этой ветки - Yuri Rus - вполне находит время, чтобы тратить его не только на изучение, но и на рассказы нам о том, к чему он пришёл. За что ему искреннее спасибо!
|
|
Yuri Rus ( Слушатель ) |
| 16 сен 2013 04:20:29 |
Это вопрос, насколько я понимаю, не ко мне лично, а ко всем. От себя могу сказать, что я считаю, что эфир есть. Русика именно об этом - см. исходные аксиомы на предыдущей странице ветки. Что же касается Ацюковского и многих других авторов теорий эфира, то, хотя я согласен с ними, что эфир есть, я или не согласен с какими-то деталями их теорий, или мне просто непонятно, откуда они взяли какие-то свои утверждения. Прежде всего, давайте не забывать, что я иду намного дальше, чем все "альтернативщики", вместе взятые: я утверждаю, что практически вся физика неверна, потому что неверны ее исходные аксиомы. В частности, неверно определение полного дифференциала (см. первые страницы ветки). Неверен Принцип Относительности Галилея (вместо него я ввожу Принцип Дуализма Движения). Физика совершенно не понимает явления аберрации (света или звука), а в русике он играет фундаментальную роль (я просто никак не могу закончить с его изложением, лишь частично описал аберрацию для звука, но еще не сделал это для света и электрического поля). Практически все альтернативщики же являются безусловными сторонниками классической физики, они пытаются описать в ее рамках те явления, которые "официальная" физика описывает с позиции теории относительности и квантовой механики.
У Ацюковского эфир - это обычный газ, а частицы представляют из себя вихри эфира. Это означает, что при движении вещества (скажем, телескопа) эфир, составляющий это вещество, движется с той же скоростью, то есть эфир полностью увлекается веществом. Опыты же по аберрации света и опыт Физо показывают, что это не так. В XIX веке было принято считать, что эти опыты доказывают, что эфир лишь частично увлекается веществом. Я собираюсь доказать, что эфир не увлекается веществом совсем.
Далее, мне совершенно непонятно, откуда, из каких соображений Ацюковский пришел, допустим, к выводу, что протон - это тороидальный вихрь эфира, окруженный температурным пограничным слоем эфира, а нейтрон - это тот же протон, дополнительно окруженный еще пограничным градиентным слоем? Где последовательные логические шаги, которые привели его к этому выводу? Очень многие другие "альтернативщики" поступают точно так же - они вываливают на читателя некую модель элементарных частиц (тороидальные вихри, кстати, очень популярны), которая неизвестно откуда взялась. Я надеюсь, что не от инопланетян (шютка).
Прошу не интерпретировать мои слова как априорное отрицание всех альтернативных гипотез и моделей. Может быть, в каких-то из этих моделей есть зерно истины. Но я лично могу тратить свое время только на те модели, каждый шаг которых обоснован и детально описан (начиная с самых исходных понятий и постулатов). Если авторы предоставляют мне только некий конечный результат, тот самый тор, я вынужден проигнорировать его, потому что мне непонятно, откуда что взялось.
При этом я считаю, что только у альтернативщиков есть надежда найти хоть какие-то ценные идеи, но не у представителей "официальной" физики. Там, полностью, на 100% одни эпициклы. Потому что физика (напоминаю, классическая, со времени Галилея) - почти полностью ошибочна. Что я и пытаюсь здесь доказать.
|
|
существо с антитентуры ( Слушатель ) |
| 16 сен 2013 12:04:58 |
Цитата: Yuri Rus от 16.09.2013 04:20:29
Ну что значит неверна, надо же и от чего-то отталкиваться. Та же кинематика. Или что может быть проще геометрической оптики, вроде все измерено и перемеряно вдоль и поперёк.
Цитата: Yuri Rus от 16.09.2013 04:20:29
Ацюковский там у себя кстати развенчивает опыт Физо и доказывает, что в то время и с теми возможностями технологии его просто невозможно было поставить.
Цитата: Yuri Rus от 16.09.2013 04:20:29
Т.е. эфир - это кристаллическая решётка? В это поверить даже потруднее, чем в газ:)
Цитата: Yuri Rus от 16.09.2013 04:20:29
Ну он вроде объяснял, что вся его теория основана на чистой логике. Почему эфир - газ он там объясняет, ну а если эфир - газ, то.... ну а дальше пошло-поехало, газовая динамика, вихри, тороиды и т.д.
Цитата: Yuri Rus от 16.09.2013 04:20:29
К сожалению тут не за что ухватиться. Нужен какой-то прибор, который позволит этот эфир поймать. Можно конечно клеймить Майкельсона и Миллера, но если они неправы, то нужна какая-то альтернатива.
|
|
существо с антитентуры ( Слушатель ) |
| 16 сен 2013 21:59:25 |
Цитата: Yuri Rus от 16.09.2013 18:55:51
Вот здесь
https://disk.yandex.…&locale=ru
на 75 странице он объясняет, почему эфир - газ.