Все врут
07 дек 2020 в 08:27
Doctor_D
|
|---|
|
https://www.medrxiv.…1.full.pdf
ЦитатаВышла занятная статья, в которой оценили, на сколько отчеты по заболеваемости ковидом в 171 странах похожи на правдивые. Очередное спасибо https://chuka-lis.livejournal.com/ за интересное.
|
|
|
ОТВЕТЫ (37)
|
|
basilevs ( Слушатель ) |
| 07 дек 2020 в 10:14 |
Цитата: Doctor_D от 07.12.2020 08:27:23
Прочитал статью. Дикий математикообразный бред. Объясняю.
Я дико извиняюсь, но с какого перепугу "Закон Берфорда" применим к коронавирусной статистике? Это правило, которое по смыслу означает, что везде события экспоненциального роста развиваются по одинаковому сценарию. А с чего это он обязан быть одинаковым? На заражаемость действует такая куча факторов, что этот закон оказыается в пролёте - там нет чистой незамутнённой экспоненты в самой сути явления.
Ну и вишенка на торте - к числу "правильных" стран по этому исследованию относятся Гаити и Афганистан. Это, видимо, страны с хорошо налаженным механизмом диагностики и высокоразвитой медицинской системой. Да уж.
Имеем типичный случай применения хорошего математического аппарата без понимания его сути. Ставим Ахмаду Килани (Department of Comparative Politics, RUDN University, Moscow - Факультет , институт Учебно-научный институт сравнительной образовательной политики Российского Университета Дружбы Народов) и Георгиусу Георгию (Department of Languages and Literature, University of Nicosia, знатный математик и спец по статистике, сразу видно!)
- +0.33 / 17
-
|
|
normalized_ ( Слушатель ) |
| 07 дек 2020 в 10:22 |
Цитата: Doctor_D от 07.12.2020 08:27:23
Любопытно, но ИМХО закон Бенфорда может быть неприменим.
Авторы считают, что числа "reported daily cases of Covid-19" у каждой страны должны подчиняться Закону Бенфорда.
Проверяют гипотезу для каждой страны критерием Хи-квадрат (согласие Пирсона), подчиняются ли "новые подтвержденные заражения за день" или нет.
Если брать массив чисел по всем странам, то наверняка подчинится. Они все разного масштаба.
Но, боюсь, что закон Бенфорда нельзя распространять на ежедневные новые подтвержденные случаи для каждой страны. Потому что данные в какие-то длительные промежутки времени находятся в каком-то естественном диапазоне, а это "звоночек" для применимости. Например, между волнами данные находятся на более-менее одном уровне и не скачут в три раза.
Рассуждения на скорую руку, возможно, ошибочные:
Чтоб проверить можно ли использовать закон Бенфорда для выявления фальсификаций, можно поиграть масштабом.
Для данных подчиняющихся Закону Бенфорда результат таблицы критериев не должен существенно измениться, если изменить масштаб.
Можно пересчитать таблицу результата критериев, разделив все исходные данные стран на заранее выбранное число. Желательно не подгоняя это число к желаемому результату, а выбрав его до эксперимента перерасчета.
В зависимости от того, насколько изменится таблица результатов, существенно ли, или вплоть до изменения у некоторых стран на противоположенные, выяснится насколько закон Бенфорда применим к рассматриваемым данным.
Например, по России июль-июнь числа новых случаев болтались около 4000-7000.
Даже если данные фальсифицировали, это не означает что реальные должны должны были болтаться от 1 000 - 20 000 на этом промежутке времени.
Критерий Хи- квадрат покажет, что данные за весь период (март-ноябрь) скорее всего выбиваются из закона Бенфорда.
За цифрами критерия скрыто, но мы понимаем почему так: слишком много пятерок и шестерок в первых цифрах ежедневно поступающих данных было летом.
За июнь-сентябрь данные практически ни разу не начинались с "1".
А если разделить данные по России на 4, то получившиеся числа за лето и сентябрь будут начинаться на "1" очень часто.
А значит, к таким данным Бенфорд, Пирсон и Фишер станут более благосклонны.
- +0.25 / 12
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 11:21 |
Он и есть неприменим. Потому что число выявленных заражений - фактически линейная функция от числа тестов.
А вот если нормировать, например "на тысячу тестов" - то уже можно посмотреть.
- +0.06 / 3
-
|
|
Alex_new ( Слушатель ) |
| 07 дек 2020 в 17:58 |
Цитата: Sergey B. от 07.12.2020 11:21:22
Он не применим уже по тому, что это не случайное распределение. А функция от смеси случайного распределения и воздействия людей. Организованного, но не равномерного.
Которое из за величины воздействия меняет скорость заражения....
Этот же спор уже был в начале пандемии. Когда уважаемый Навигатор искал общее в приведенных графиках заражений по странам и на основании опыта КНР утверждал, о победе над вирусом на 90 день.
В КНР то победили- так как применяли соответствующие меры- другие , кто не применял, получили, что имеем...
Личная точка зрения.
- +0.07 / 4
-
|
|
normalized_ ( Слушатель ) |
| 07 дек 2020 в 21:56 |
Цитата: Sergey B. от 07.12.2020 11:21:22
Нет, не линейная.
Вот, пожалуйста, посмотрите:
На пером изображении показано отношение числа потраченных тестов на число выявленных. накопительным итогом (с марта):
В Латвии 157, в России около 40, где-то 2.
И меняется во времени .
Если бы было линейно по странам, то весь пучок линий был бы узким, и горизонтальным.
На втором изображении тоже самое, но в среднем за неделю.
Разница "линейности" в странах от 2 до 5000.
И даже в пределах одной страны может на несколько порядков зависеть от даты, (т.е. и от ситуации)
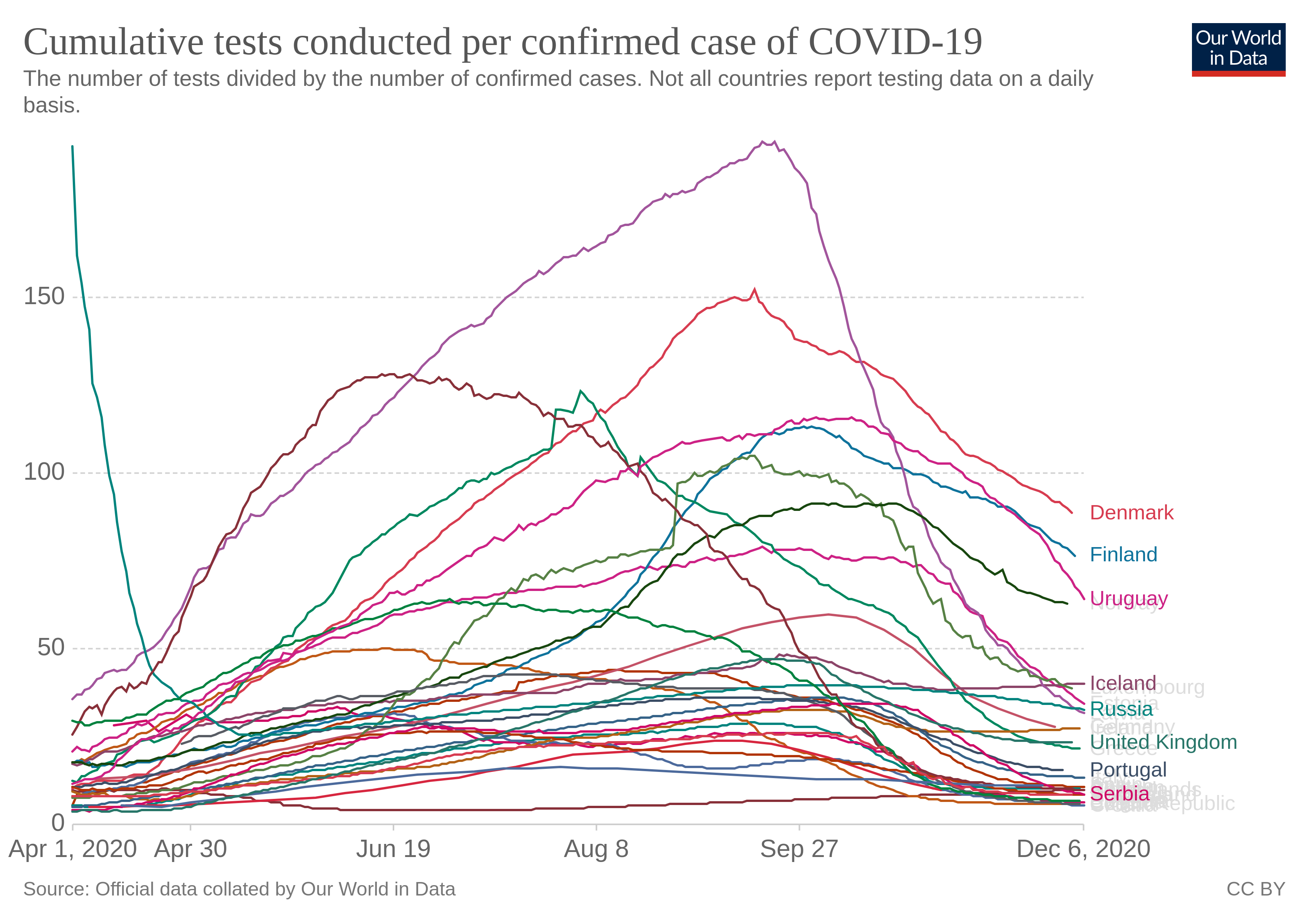
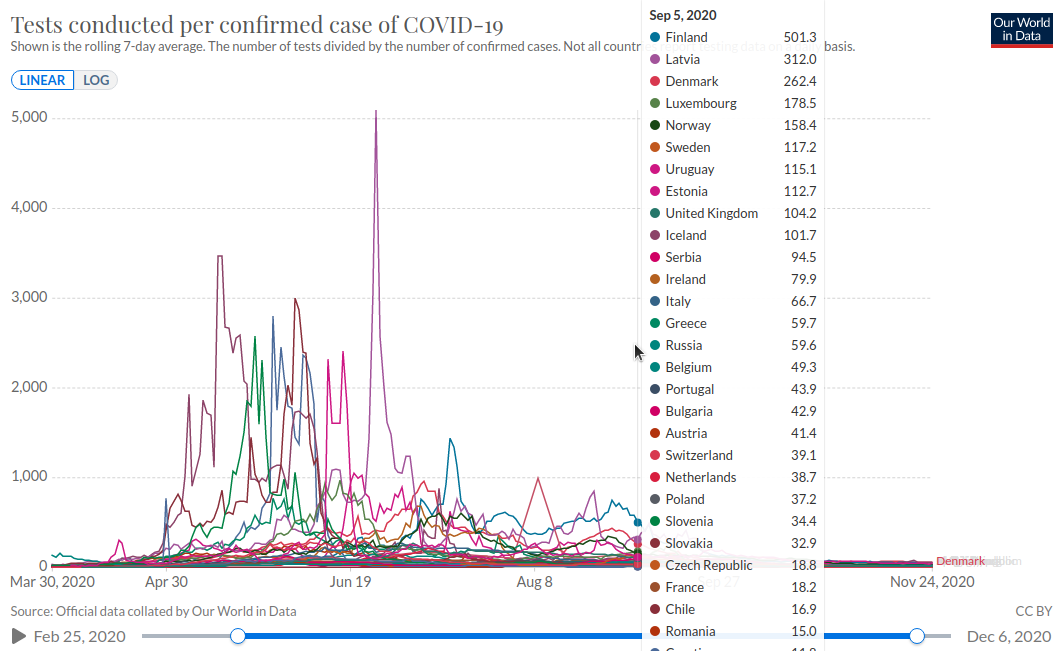
Ссылка
- +0.08 / 4
-
|
|
Doctor_D ( Слушатель ) |
| 07 дек 2020 в 11:23 |
Ну, поскольку я ни разу не статистик и еще меньше- математик
 я и вынес материал на суд общественности.
я и вынес материал на суд общественности.По моему внутреннему убеждению, абсолютно достоверных данных не предоставляет никто: вопрос очень политизирован (факторы и внутренней и внешней политики), плюс сильное влияние на экономику всех публикуемых цифр, что создает соблазн поиграться с биржами.
Плюс, во многих местах фактор недостатка ресурсов и/или общего раздолбайства и низкой квалификации.
- +0.12 / 6
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 11:27 |
Цитата: Doctor_D от 07.12.2020 11:23:59
Чтобы предоставить наиболее достоверные данные, необходимо ежедневное тестирование всего населения.
 Иначе можно говорить лишь о некоей величине, которая в своем абсолютном значении ни о чем не говорит.
Иначе можно говорить лишь о некоей величине, которая в своем абсолютном значении ни о чем не говорит.Т.е., в качестве примера:
Берем вчерашний день vs 12.05.2020
1 Итерация:
Абсолютные цифры - 29039 vs 10899
Кошмар, больных в 3 раза больше.
2 Итерация - нормируем на количество тестов на одного выявленного:
19 vs 15
Ништяк, больных на 20% меньше чем весной
А что в реальности - исходя из этих двух цифр вообще нельзя сказать. Можно очень приблизительно посчитать, высказав кучу предположений, от каждого из которых оптимизм может превратится в пессимизм и наоборот. Например - надо смотреть - кого тестировали тогда и сейчас и вносить поправку на это, вычесть отболевших и имеющих иммунитет ( предположив, что он сохранился за полгода ) и еще стопиццот параметров. Я вообще не понимаю, зачем эти цифры публикуют если честно.
- +0.11 / 6
-
|
|
Doctor_D ( Слушатель ) |
| 07 дек 2020 в 11:40 |
Цитата: Sergey B. от 07.12.2020 11:27:15
Ну, это- что то близкое к сферическому в вакууме.
Основное, пожалуй, вопрос стандартизации. Из-за него очень трудно сравнивать данные между странами.
Результаты тестирования, вообще, очень сильно зависят от применяемых подходов (кого, когда и сколько тестировать), от качества самих тестов и методик их выполнения.
Более объективные показатели- число больных в реанимации/ на ИВЛ/ умерших. Последний показатель, увы, открывает простор для манипуляций, как и, например, общее число госпитализированных (если не учитывать показания к госпитализации, которые меняются, в т.ч. и полуофициально).
- +0.08 / 4
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 11:48 |
Цитата: Doctor_D от 07.12.2020 11:40:57
Ни разу не объективен. Просто потому что не с чем сравнивать - опыта "А что будет, если заставить на полгода население вести малоподвижный образ жизни в масках" нет ни у кого. Нет некоего уровня отсчета.
- +0.10 / 6
-
|
|
Doctor_D ( Слушатель ) |
| 07 дек 2020 в 12:15 |
Цитата: Sergey B. от 07.12.2020 11:48:52
Что такое "малоподвижный образ жизни в масках" и как оно связано с смертью от коронавируса?
И откуда полгода?
- +0.04 / 5
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 12:34 |
Цитата: Doctor_D от 07.12.2020 12:15:56
1. С апреля примерно сего года, сидим дома на удаленной работе всю весну, все время ходим в масках, иначе остракизм и штрафы. Уже больше чем полгода, да.
2. Ну я например уже 5 лет не болел осенне/весенними простудами - однако в этом году за первую половину нажрал 5 кг, за осень вроде скинул - однако неделю с соплями отходил все равно. Так я принудительно вгоняю себя в движение, каждый день тренировочки, днем раз в три часа встал и прошел километрик, на выходных придумал как подвигаться, и маску напяливаю только в случае необходимости - т.е. для избежания штрафов и в местах естественного скопления больных ( не "скопления людей" ) вроде поликлиники. А средний лежатель на диване, которого еще и принуждают лежать - испортил себе здоровье намного больше. Поехавшие крыши запертых в одном помещении людей. Плюс хроники всякие, не получившие вовремя лечения, обездвиженная, по сути, "группа риска". Сколько трупиков избыточной смертности прибавило это?
- +0.14 / 22
-
|
|
Doctor_D ( Слушатель ) |
| 07 дек 2020 в 12:41 |
Цитата: Sergey B. от 07.12.2020 12:34:38
1. И что? У вас отменились походы от рабочего места до кулера и обратно?
 Где вы "все время" ходите в маске в таком случае? Неужели, поход в ближайшую Пятерочку раз в пару дней вас так страшно напрягает? Или мы что то не знаем про вашу маску? Брезент в четыре слоя?
Где вы "все время" ходите в маске в таком случае? Неужели, поход в ближайшую Пятерочку раз в пару дней вас так страшно напрягает? Или мы что то не знаем про вашу маску? Брезент в четыре слоя?
2. Тот, кто занимался физическими нагрузками, тот занимался ими даже в самые жесткие периоды самоизоляции. Кто лежал на диване- лежит и сейчас. Ничего не изменилось.
Плановые операции на то и плановые, что не экстренные. И без их выполнения не умирают. Хроники получали свое лечение. В случае обострения- они переставали быть хрониками и ехали в больницу.
Так что вы трупики ищете совсем не там.
- +0.14 / 21
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 12:59 |
Цитата: Doctor_D от 07.12.2020 12:41:38
1. Да. В условиях самоизоляции я просыпаюсь на рабочем месте. И по квартире не особо походишь. И поход в пятерочку не напрягает. А вот отсутствие часа танцев в день, либо прогулок на экскурсиях в соседний город - напрягало. И что значит маска из брезента? Обычная хрень из аптеки, бессмысленная, беспощадная и мешающая дышать.
2. Очень сложно даже приблизительно нагрузится в квартире так-же как вне нее. Даже если стараться.
Про хроников не рассказывайте. У меня таких трое.
- +0.08 / 17
-
|
|
Doctor_D ( Слушатель ) |
| 07 дек 2020 в 13:10 |
Цитата: Sergey B. от 07.12.2020 12:59:36
1. Вы на самоизоляции по контакту с больным? Тогда какая вам, нах, Пятерочка, даже в маске? Вы каждый день ходили на танцы? Как мило...
 Акробатический рок-н-ролл, как я полагаю, если в квартире не получается?
Акробатический рок-н-ролл, как я полагаю, если в квартире не получается?А прогулки вам кто запретил?
Вы знаете, мои родители, пожилые люди, но привыкли гулять пару раз в день. И в апреле-мае тоже гуляли. С соблюдением дистанции и всего прочего. Запрета на выход из дома не вводилось, если что.
И не рассказывайте мне про маски. Я в них по работе почти каждый день по 5-8 часов. И не в маске, а в респираторе. Потому что риск контакта с больным высокий, а заразу домой принести очень не хочется. И знаете что- нормально дышится. Вообще без проблем.
Может, вам стоит стать чуть-чуть менее хлюпиком?

2. Ну, если вы атлет и привыкли к ежедневному кроссфиту... Обеспечить привычный уровень нагрузки обычного человека- вообще никаких проблем нет. Было бы желание.
В чем была проблема с вашими хрониками? Их не брали в больницу по показаниям? Не пускали в аптеку за привычными лекарствами?
- +0.23 / 15
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 13:16 |
Цитата: Doctor_D от 07.12.2020 13:10:10
1. Вы, может, не заметили, но весной она, самоизоляция, была у всех. Танцевать - в одиночку очень нелепо и не нагружает.
2. Так страшно. Рекомендовали не шлятся, а далеко тем более. И привычный уровень нагрузки обычного человека - 200 метров мышкой и жим бутылки пива вечером - меня не устраивает.
- +0.06 / 8
-
|
|
Doctor_D ( Слушатель ) |
| 07 дек 2020 в 13:28 |
Цитата: Sergey B. от 07.12.2020 13:16:30
1. Я, например, сразу купил велотренажер и крутил педали по часу-полтора в день. Нормальная нагрузка. Не танцы, конечно. Но- было бы желание, как я уже говорил.
У меня перед глазами пример одного жулика.
 Отсидел почти три года в СИЗО за мошенничество. Похудел на 30 кг, накачал мышцы, выучил разговорный английский (он ему был нужен, чтобы жалобу в ЕСПЧ писать) и, кажется, даже что-то заочное по юриспруденции закончил. Вот такая у него самоизоляция вышла. В камере. С прогулками в закрытом дворике по часу раз в два дня.
Отсидел почти три года в СИЗО за мошенничество. Похудел на 30 кг, накачал мышцы, выучил разговорный английский (он ему был нужен, чтобы жалобу в ЕСПЧ писать) и, кажется, даже что-то заочное по юриспруденции закончил. Вот такая у него самоизоляция вышла. В камере. С прогулками в закрытом дворике по часу раз в два дня.2. Бояться глупо. А гулять было можно и не далеко от дома. Кто хотел- тот гулял.
- +0.18 / 16
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 13:34 |
Цитата: Doctor_D от 07.12.2020 13:28:56
1. Нагрузка интересна, когда она не тупая. Велотренажер - туп. У меня был аналог этого, танцы в одиночку по удаленке. Не то.
СИЗО и желание занятся "хоть чем-то" совсем не равносильны "работа дома и рекомендации не выходить на улицу".
2. Боятся штрафа за отсутствие маски - не глупо. Или кода разрешения. А вируса я опасался где-то в феврале, когда еще не было ясно насколько он опасен и все такое. В апреле то какой смысл его боятся был?
- +0.00 / 15
-
|
|
Kris ( Слушатель ) |
| 08 дек 2020 в 13:54 |
Цитата: Doctor_D от 07.12.2020 13:28:56
Вот Вы хрень пишите. Ваш оппонент писал о всем населении в целом, а Вы в качестве аргумента противного приводите пример как должна (и поступает) активная часть населения, которая имеет силу воли заботится о своей физической форме. И эта часть не сказать чтобы большая, основная масса будет что-то делать только под принуждением, явным или не очень. Вот не на что кушать, ему приходиться ходить на работу, там тоже придется подвигаться в той или иной степени, вечером может тоже куда-нибудь иногда сходить когда всякие заведения открыты, в общем хоть какая-то движуха. А сейчас и этого нет. Или Вы не согласны с констатацией факта, что количество физических нагрузок у большой части населения за время эпидемии резко сократилось?
- +0.02 / 11
-
|
|
Doctor_D ( Слушатель ) |
| 08 дек 2020 в 14:20 |
Цитата: Kris от 08.12.2020 13:54:17
Нет, не согласен. Проблемы были только у тех, для кого "движуха" это "сходить во всякие заведения". Но этот контингент и дома занятие находил.
А так- кто хотел двигаться, тот двигался. Кто лежал на диване - и сейчас лежит.
- +0.22 / 12
-
|
|
Kris ( Слушатель ) |
| 08 дек 2020 в 18:40 |
Цитата: Doctor_D от 08.12.2020 14:20:24
Неа, теперь он лежит на диване больше и чаще. И если Вы этого в упор не видите, то таки да, обсуждать больше нечего.
- +0.09 / 10
-
|
|
ОкоСан ( Слушатель ) |
| 08 дек 2020 в 14:21 |
Цитата: Kris от 08.12.2020 13:54:17
Добавьте сюда состояние стресса, в котором длительное время находится человек.
- +0.08 / 5
-
|
|
Doctor_D ( Слушатель ) |
| 08 дек 2020 в 14:46 |
Цитата: ОкоСан от 08.12.2020 14:21:52
Почему вы легкое беспокойство называете стрессом?
А что с вами будет, если случится, не дай бог, действительно, стрессовая ситуация?
Вот у них, например- стресс:

А у вас:

Не стресс. Уж простите.
- +0.21 / 6
-
|
|
ОкоСан ( Слушатель ) |
| 08 дек 2020 в 15:05 |
Цитата: Doctor_D от 08.12.2020 14:46:33
Ваше легкое беспокойство? В Вашем случае логичнее рассмотреть проф. деформацию
Со мной дипломированный практикующий психолог рядом, потому ничего не случится.
По остальной части народонаселения читайте статистику ВОЗ по депрессиям.
- +0.05 / 3
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 13:22 |
Цитата: Doctor_D от 07.12.2020 13:10:10
"Приходите после эпидемии", А и Б не принимают ....
А, ну и еще стадо напуганных идиотов выносит аптеки.
Бессмысленный спор.
- +0.06 / 9
-
|
|
Doctor_D ( Слушатель ) |
| 07 дек 2020 в 13:33 |
Цитата: Sergey B. от 07.12.2020 13:22:33
Слушайте. У меня родители чуть младше 80 лет.
Кого вы лечите?

Не было никаких проблем с медпомощью. Сами старались без нужды в поликлинику не ходить, ибо нефиг. А зачем? Лечение расписано, таблетки куплены/получены. Скорая в экстренном случае приехала. Потребовалась госпитализация- отвезли, положили.
- +0.01 / 4
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 13:36 |
Цитата: Doctor_D от 07.12.2020 13:33:16
Найдите мне 3х1мл. метипреда в капельницы. Можно 12*0.25
- +0.07 / 5
-
|
|
Danilov71 ( Слушатель ) |
| 07 дек 2020 в 13:40 |
Цитата: Sergey B. от 07.12.2020 12:59:36
Кто хочет — ищет способы, кто не хочет — причины» (Сократ)
- +0.01 / 11
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 13:41 |
Цитата: Danilov71 от 07.12.2020 13:40:11
Мотивационными заклинаниями лечите гуманитариев в соответствующих ветках
 Я всю жизнь их использую для направления людей в нужное русло, так что цену им знаю.
Я всю жизнь их использую для направления людей в нужное русло, так что цену им знаю.
- +0.07 / 11
-
|
|
Danilov71 ( Слушатель ) |
| 07 дек 2020 в 15:52 |
Цитата: Sergey B. от 07.12.2020 13:41:57
А сами себя, следовательно, мотивировать не можете? Сапожник без сапог?
- +0.07 / 4
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 15:57 |
Цитата: Danilov71 от 07.12.2020 15:52:12
Т.е. вы предлагаете:
1 - заняться чем то неинтересным либо
2 - нарушить кучу рекомендаций и указов.
Мотивировать на исполнение неинтересного можно либо легковерного идиота - мотивашками, либо зависимого от чего-то человека - шантажом в той или иной форме. Любая мотивация работает именно так.
- +0.01 / 10
-
|
|
Sergey B. ( Слушатель ) |
| 07 дек 2020 в 16:14 |
Цитата: Danilov71 от 07.12.2020 16:01:13
Мне неинтересно это делать неинтересными мне методами. Заставить себя - могу. Но это - скучно. Процесс важен. Как бы это попонятнее - мне неинтересно делиться, потому что бог так велел - я делюсь там где вижу что это поможет. Мне неинтересно скорбеть о миллионах голодающих детей в Африке. Мне неинтересно потеть бегая марафоны или крутя педали велотренажера только потому, что надо напугать миллионы людей ( и я понимаю зачем надо их напугать, и даже одобряю методику - но только сам не хочу в этом карнавале абсурда участвовать ).
- +0.01 / 11
-
|
|
Cheen ( Слушатель ) |
| 07 дек 2020 в 19:43 |
Цитата: Sergey B. от 07.12.2020 16:14:12
Нам каГбэ тоже тоже не интересны страдания "танцоров выходного дня". И ???
- +0.10 / 12
-
|
|
Sergey B. ( Слушатель ) |
| 08 дек 2020 в 07:29 |
Цитата: Cheen от 07.12.2020 19:43:30
"Я гналась за вами три дня" - сказать то вы что хотели?
- +0.05 / 3
-
|
|
D_K ( Слушатель ) |
| 07 дек 2020 в 11:39 |
Конечно неприменим. Он более менее работает при экспоненциальном росте (именно поэтому на мировых данных и работает). Как только заболеваемость выходит на плато или снижается, а я думаю что никто не спорит, что летнее снижение было реальным, Бенфорд перестает работать.
- +0.11 / 4
-
