Жизнь, Разум, Человек, Религия и Наука
144,945
565
|
|
Yuri Rus ( Слушатель ) |
| 24 май 2011 07:54:00 |
Тред №324429
новая дискуссия Дискуссия 194
Чему равна сила звукового давления ΔF, действующая на элемент объема? Напомню, мы рассматриваем упрощенный вариант, где величина pₐ практически не меняется: pₐ ≈ const.
Вначале рассмотрим, чему равна сила звукового давления, создаваемая покоящимся источником. Волны давления разбегаются от источника, но поскольку мы считаем, что pₐ ≈ const, то на смену одной волне тут же приходит другая, с тем же самым значением давления в этой точке. Соответственно, сила давления в этой точке тоже будет примерно константой. Поэтому, мы можем убрать индексы 1, 2, 3… единичных волн, а писать просто p₀ и ΔF₀ (0 обозначает СО покоящейся среды); они не зависят от времени. Эта ситуация аналогична электростатике в классической физике, потому она для нас особо интересна. Можно сказать, что классическая электростатика описывает источник с бесконечной длиной волны (в квантовой механике появляются длины волн Де Бройля и Комптона).
Очевидно, сила ΔF₀ должна быть обратно пропорциональна квадрату расстояния r от источника, так же, как сила гравитации и Кулоновская сила. Величина же звукового давления p₀ обратно пропорциональна расстоянию от источника:
p₀ = pₐa / r = pₐa / (ct)
ΔF₀ = – ∇p ΔxΔyΔz = (pₐa r / r³) ΔxΔyΔz = (pₐa c / (c³t²)) ΔxΔyΔz
Допустим, на оси х давление в точках (x, 0, 0) и (x – Δx, 0, 0) равно
p₀(x, 0, 0) = pₐa/x
p₀(x – Δx, 0, 0) = pₐa/(x – Δx)
Δp₀/Δx = (p₀(x, 0, 0) – p₀(x – Δx, 0, 0))/Δx =
= (1 – 1/(1 – Δx/x)) pₐa/(x Δx) ≈ (1 – (1 + Δx/x)) pₐa/(x Δx) = – pₐa/x²
Рассмотрим теперь источник, движущийся по оси х со скоростью v. Обозначим β = v/c. Пусть в момент времени t=0 источник находился в начале координат и излучил первую единичную волну, которая за время t₁ распространилась во все стороны на расстояние r₁’(t₁) = ct₁ (в СО покоящейся среды) и образовала сферическую поверхность, во всех точках которой звуковое давление одинаково и равно
p₁(t₁) = pₐa / r₁’(t₁) = pₐa / (ct₁)
Штрих у r₁’ введен для единообразия обозначений с книгой Фейнмана, чтобы легче было сравнивать.
Чему будет равна сила, создаваемая звуковым давлением в точке Q₁(x₁, y₁, z₁) на этой сфере? Пусть угол между направлением движения источника и направлением от источника к точке Q₁ в момент излучения равен α₁. Казалось бы, можно просто воспользоваться формулой
ΔF₁ = – ∇p₁ ΔxΔyΔz = (pₐa r₁'/r₁’³) ΔxΔyΔz
Но это не так – дело в том, что выражение для p₁ относится только к одной единичной волне, распространение которой удовлетворяет уравнению
r₁'(t) = ct = i x(t) + j y(t) + k z(t)
Как я детально объяснял ранее, точки (x, y, z) и (x – dx, y, z) относятся либо к разным моментам времени у одной единичной волны, либо к разным единичным волнам в один момент времени. Градиент же давления, по определению, мы должны искать в один и тот же момент времени, но в разных точках пространства. Следовательно, чтобы найти градиент давления в точке Q₁ в определенный момент времени, мы должны использовать не одну, а, как минимум, две разных единичных волны.
В момент времени dt источник излучает вторую единичную волну:
r₂’(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
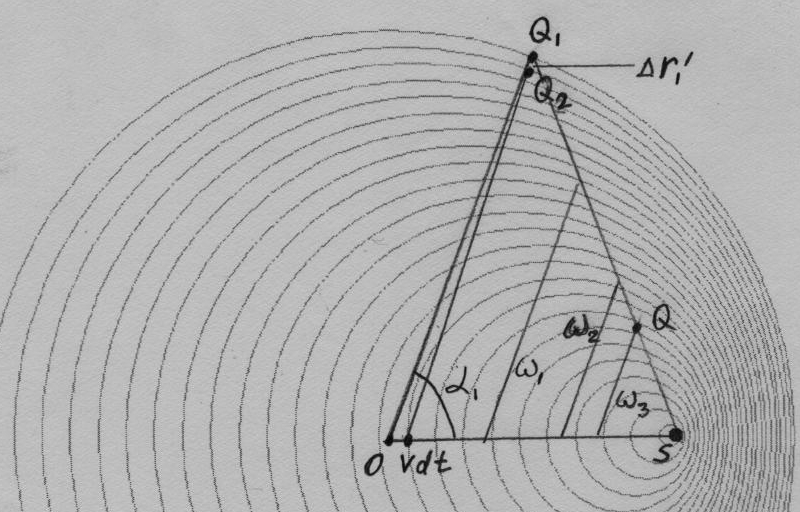
За время dt, источник сместился на расстояние v dt по оси х от начала координат. Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке Q₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки Q₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию вектора v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – β cos α₁)
При этом, давление во всех точках сферы, образованной второй единичной волной, в момент t₁ равно
p₂(t₁) = pₐa / |r₂’(t₁) – v dt| = pₐa / (c (t₁ – dt))
Вектор градиента давления должен быть параллелен нормали к эквипотенциальной поверхности (поверхности равного давления). Поскольку мы исходим из предположения, что фронт каждой волны совпадает с эквипотенциальной поверхностью, то градиент давления в каждой точке будет параллелен вектору r'. Это означает, что градиент давления можно найти, просто продифференцировав Δp по Δr’ в каждой точке (в один и тот же момент времени). Для точки Q₁(x₁, y₁, z₁) это будет:
Δp₁(x₁, y₁, z₁, t₁) / Δr₁’ = (p₁(t₁) – p₂(t₁)) / (c dt (1 – β cos α₁)) =
= – pₐa / (r₁’² (1 – β cos α₁)) = – pₐa / ((c t₁)² (1 – β cos α₁))
ΔF₁(x₁, y₁, z₁, t₁) = pₐa r₁' / (r₁’³ (1 – β cos α₁)) ΔxΔyΔz = pₐa c / (c³t₁² (1 – β cos α₁)) ΔxΔyΔz
Кстати:
1 / (1 – β cos α₁) ≡ 1 / (1 – r₁'∙v / (r₁’c))
То есть, как видите, множитель вида 1 / (1 – r'∙v / (r’c)) у нас все-таки появился. Но он появился не для давления (то есть потенциала), а для силы давления. Есть разница (об этом ниже).
Вектор r₁' и угол α₁ относятся к положению источника в запаздывающий, нулевой момент времени, тогда как давление p₁ и сила ΔF₁ определяются в момент времени t₁. За время t₁, пока волна проходила расстояние r₁’ до точки Q₁, источник сместился по оси х на расстояние vt₁ = βr₁’ от начала координат. Обозначим расстояние от источника S(vt₁, 0, 0) до точки Q₁ (x₁, y₁, z₁) как r₁:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
Далее обозначим
u₁ = x₁ – vt₁ = x₁ – βr₁’.
Давайте перепишем уравнения для p₁ и ΔF₁ в точке Q₁ относительно r₁, u₁, y₁, и z₁, вместо r₁’, x₁, y₁, и z₁, то есть относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Воспользуемся уравнением:
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁² ,
Раскрыв скобки и перенеся все налево, мы можем выразить r₁' через u₁, y₁, z₁ и β путем решения квадратного уравнения
(1 – β²) r₁’² – 2 β u₁ r₁’ – (u₁² + y₁² + z₁²) = 0
Получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
Давление в точке Q₁ тогда равно:
p₁ = pₐa/r₁’ = pₐa (1 – β²) / (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)
Так же мы можем выразить ΔF₁ (в скалярной форме) через u₁, y₁, z₁ и β:
cos α₁ = x₁ / r₁'
А поскольку x₁ = u₁ + βr₁’ , то
cos α₁ = β + u₁ / r₁’
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
ΔF₁ = pₐa / (r₁’² (1 – β cos α₁)) ΔxΔyΔz =
= pₐa / ((β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
В векторной форме, ΔF₁ нужно умножить на единичный вектор в направлении r₁':
ΔF₁ = ΔF₁ r₁'/r₁' = ΔF (r₁ + vt₁) / |r₁ + vt₁| = pₐa (r₁ + vt₁) / (|r₁ + vt₁| (β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
Получилось довольно громоздкое выражение. Однако, все эти x₁, y₁, z₁, u₁, t₁ – не переменные, а фиксированные значения. Они относятся только к одной единичной волне, к одному моменту времени и к трем точкам (начало координат О, положение источника в момент t₁ и точка Q₁). Как будут выглядеть уравнения для p и ΔF для разных моментов времени, где x, y, z, u, t – это переменные, а не фиксированные значения?
Проведем прямую линию от положения источника в момент времени t₁ (точка S) к точке Q₁ (первая единичная волна из начала координат достигает ее также в момент t₁). Попробуем определить, чему равны давление p и сила ΔF в момент t₁ в других точках прямой SQ₁. Введем переменные при помощи переменного коэффициента ω:
u = ω u₁
Из вышеприведенного рисунка (где нарисованы первая и вторая единичные волны, точки О, S, Q₁ и Q₂) видно, что тогда остальные переменные, относящиеся к этой прямой и к моменту t₁, тоже можно выразить через ω (ω₁, ω₂, ω₃ – разные значения):
y = ω y₁ z = ω z₁ r = ω r₁
Давление в произвольной точке Q(u, y, z) будет равно
p = p₁ / ω = pₐa (1 – β²) / (ω (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)) =
= pₐa (1 – β²) / (ω (β u/ω + ((u/ω)² + (1 – β²) ((y/ω)² + (z/ω)²))½)) =
= pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
Аналогично, для силы мы получим
ΔF = pₐa / ((β u / (1 – β²)½ + (u² / (1 – β²) + y² + z²)½) (u² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Очень хорошо, мы избавились от ω и оказалось, что для переменных x, y, z, u это уравнение выглядит точно так же, как и для фиксированных значений x₁, y₁, z₁, u₁. А поскольку угол α₁ в первоначальном уравнении мог быть произвольным и он определялся соотношением между x₁ и r₁’, то уравнения для p и ΔF справедливы не только для прямой SQ₁, но во всем пространстве. Заметим, что время t₁ или t в этих уравнениях вообще не фигурирует, потому что они записаны для системы отсчета источника, и здесь на место одной единичной волны сразу же приходит другая, с теми же значениями p и ΔF (см. выше об источнике в СО покоящейся среды и аналогии с электростатикой).
Однако время, безусловно, должно фигурировать в уравнениях для СО покоящейся среды. Давайте совершим обратный переход в эту СО. Заменим
u = x – vt
где vt – это положение источника в момент t.
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½) =
= pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
ΔF = pₐa / ((β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
ΔF = pₐa (r + vt) / (|r + vt| (β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Читатель, конечно, уже обратил внимание, что здесь «напрашивается» та же самая замена, что и в преобразовани Лоренца для координаты:
x' = (x – vt)/(1 – β²)½ = γ (x – vt)
Да, уравнения для p и ΔF при этом немного упростятся:
p = pₐa / (γ (β x' + (x'² + y² + z²)½)
ΔF = pₐa / ((β x' + (x'² + y² + z²)½) (x'² + y² + z²)½) ΔxΔyΔz
Ну и что? Что это нам дает? Абсолютно ничего. А вот на что следует обратить особое внимание, это на то, что уравнения в СО покоящейся среды и в СО источника выглядят совершенно одинаково по форме и переход между ними осуществляется согласно преобразованию Галилея:
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
↓
p = pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
Уравнения для ΔF в разных системах отсчета выглядят тоже одинаково. В уравнениях в обеих СО, есть и (1 – β²), и β, и корень квадратный – в одинаковых местах. Более того, для вывода этих уравнений нам понадобилось перейти из СО покоящейся среды в СО источника при помощи преобразования Галилея, а потом обратно.
Между прочим, обратите внимание, что эти уравнения вовсе не описывают распространение сферических волн со скоростью c. Они описывают эквипотенциальные поверхности, которые, хотя и совпадают с мгновенным снимком фронтов волн, в отличие от последних, «заморожены» относительно источника. В СО источника, эквипотенциальные поверхности неподвижны. В СО покоящейся среды, они двигаются вместе с источником, с той же скоростью v. Как я уже говорил, это происходит потому, что на место одной единичной волны с определенными значениями p и ΔF тут же приходит другая волна, с теми же значениями. Это не статика в том смысле, что никакого движения нет; это динамическое равновесие.
Что касается фронтов волн, то они двигаются и в СО источника. Выведем формулу их распространения.
В СО покоящейся среды, фронты волн распространяются по формуле:
(x – ξ)² + y² + z² = c²(t – ԏ)²
где ξ – координата источника по оси x в момент времени ԏ, когда была излучена соответствующая единичная волна. Если источник движется с постоянной скоростью v, то ξ = vԏ.
При переходе в СО источника, мы должны воспользоваться преобразованием Галилея
u = x – vt или x = u + vt
Получим
(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²
Чтобы смысл этого уравнения был более понятен, запишем его немного по-другому, через единичные волны. Пусть первая единичная волна была излучена в момент dt (а не в нулевой, как я раньше писал; сейчас я меняю нумерацию ради получения более простого уравнения, чтобы там не было i -1), вторая – в момент 2 dt, третья – в момент 3 dt, а i-ая – в момент i dt. Тогда уравнение распространения i-ой волны можно записать как
(x – v i dt)² + y² + z² = c² (t – i dt)²
где ԏ = i dt, ξ(ԏ) = v i dt.
Перейдем в СО источника, произведя замену x = u + v t:
(u + v (t – i dt))² + y² + z² = c² (t – i dt)²
Это уравнение, действительно, описывает те самые сферические единичные волны, распространяющиеся со скоростью c и «сдуваемые» встречным ветром со скоростью –v. Так что описание волн давления в обеих СО выглядит полностью аналогичным. Галилей рулит.
Напомню еще раз, что всё это относится к упрощенному случаю очень большой длины волны, где мы можем считать, что давление на поверхности источника pₐ ≈ const, причем pₐ > 0. Пара слов о случае, когда pₐ < 0 и при этом pₐ ≈ const. Здесь просто зеркальное отражение случая pₐ > 0. Вся разница в том, что силовые линии направлены не от источника, а к источнику. Все остальное то же самое – силовые линии искривляются точно так же, все формулы просто меняют знаки плюс на минус и наоборот.
В случае переменного давления, когда pₐ более не константа и постоянно меняет знак, формулы для звукового давления p и силы ΔF более выполняться не будут, они будут иметь более сложный характер. На каком-то участке волны сила ΔF будет направлена от источника, на другом участке – к источнику (точнее, к той точке, где был источник в момент излучения данной единичной волны).
Но что важно: силовые линии останутся теми же самыми, искривленными точно так же (хотя на каждой силовой линии ΔF будет многократно менять знак и величину). Потому что фронты волн давления, совпадающие с эквипотенциальными поверхностями, будут распространяться точно так же, а сила перпендикулярна эквипотенциальным поверхностям.
Вначале рассмотрим, чему равна сила звукового давления, создаваемая покоящимся источником. Волны давления разбегаются от источника, но поскольку мы считаем, что pₐ ≈ const, то на смену одной волне тут же приходит другая, с тем же самым значением давления в этой точке. Соответственно, сила давления в этой точке тоже будет примерно константой. Поэтому, мы можем убрать индексы 1, 2, 3… единичных волн, а писать просто p₀ и ΔF₀ (0 обозначает СО покоящейся среды); они не зависят от времени. Эта ситуация аналогична электростатике в классической физике, потому она для нас особо интересна. Можно сказать, что классическая электростатика описывает источник с бесконечной длиной волны (в квантовой механике появляются длины волн Де Бройля и Комптона).
Очевидно, сила ΔF₀ должна быть обратно пропорциональна квадрату расстояния r от источника, так же, как сила гравитации и Кулоновская сила. Величина же звукового давления p₀ обратно пропорциональна расстоянию от источника:
p₀ = pₐa / r = pₐa / (ct)
ΔF₀ = – ∇p ΔxΔyΔz = (pₐa r / r³) ΔxΔyΔz = (pₐa c / (c³t²)) ΔxΔyΔz
Допустим, на оси х давление в точках (x, 0, 0) и (x – Δx, 0, 0) равно
p₀(x, 0, 0) = pₐa/x
p₀(x – Δx, 0, 0) = pₐa/(x – Δx)
Δp₀/Δx = (p₀(x, 0, 0) – p₀(x – Δx, 0, 0))/Δx =
= (1 – 1/(1 – Δx/x)) pₐa/(x Δx) ≈ (1 – (1 + Δx/x)) pₐa/(x Δx) = – pₐa/x²
Рассмотрим теперь источник, движущийся по оси х со скоростью v. Обозначим β = v/c. Пусть в момент времени t=0 источник находился в начале координат и излучил первую единичную волну, которая за время t₁ распространилась во все стороны на расстояние r₁’(t₁) = ct₁ (в СО покоящейся среды) и образовала сферическую поверхность, во всех точках которой звуковое давление одинаково и равно
p₁(t₁) = pₐa / r₁’(t₁) = pₐa / (ct₁)
Штрих у r₁’ введен для единообразия обозначений с книгой Фейнмана, чтобы легче было сравнивать.
Чему будет равна сила, создаваемая звуковым давлением в точке Q₁(x₁, y₁, z₁) на этой сфере? Пусть угол между направлением движения источника и направлением от источника к точке Q₁ в момент излучения равен α₁. Казалось бы, можно просто воспользоваться формулой
ΔF₁ = – ∇p₁ ΔxΔyΔz = (pₐa r₁'/r₁’³) ΔxΔyΔz
Но это не так – дело в том, что выражение для p₁ относится только к одной единичной волне, распространение которой удовлетворяет уравнению
r₁'(t) = ct = i x(t) + j y(t) + k z(t)
Как я детально объяснял ранее, точки (x, y, z) и (x – dx, y, z) относятся либо к разным моментам времени у одной единичной волны, либо к разным единичным волнам в один момент времени. Градиент же давления, по определению, мы должны искать в один и тот же момент времени, но в разных точках пространства. Следовательно, чтобы найти градиент давления в точке Q₁ в определенный момент времени, мы должны использовать не одну, а, как минимум, две разных единичных волны.
В момент времени dt источник излучает вторую единичную волну:
r₂’(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
За время dt, источник сместился на расстояние v dt по оси х от начала координат. Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке Q₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки Q₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию вектора v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – β cos α₁)

При этом, давление во всех точках сферы, образованной второй единичной волной, в момент t₁ равно
p₂(t₁) = pₐa / |r₂’(t₁) – v dt| = pₐa / (c (t₁ – dt))
Вектор градиента давления должен быть параллелен нормали к эквипотенциальной поверхности (поверхности равного давления). Поскольку мы исходим из предположения, что фронт каждой волны совпадает с эквипотенциальной поверхностью, то градиент давления в каждой точке будет параллелен вектору r'. Это означает, что градиент давления можно найти, просто продифференцировав Δp по Δr’ в каждой точке (в один и тот же момент времени). Для точки Q₁(x₁, y₁, z₁) это будет:
Δp₁(x₁, y₁, z₁, t₁) / Δr₁’ = (p₁(t₁) – p₂(t₁)) / (c dt (1 – β cos α₁)) =
= – pₐa / (r₁’² (1 – β cos α₁)) = – pₐa / ((c t₁)² (1 – β cos α₁))
ΔF₁(x₁, y₁, z₁, t₁) = pₐa r₁' / (r₁’³ (1 – β cos α₁)) ΔxΔyΔz = pₐa c / (c³t₁² (1 – β cos α₁)) ΔxΔyΔz
Кстати:
1 / (1 – β cos α₁) ≡ 1 / (1 – r₁'∙v / (r₁’c))
То есть, как видите, множитель вида 1 / (1 – r'∙v / (r’c)) у нас все-таки появился. Но он появился не для давления (то есть потенциала), а для силы давления. Есть разница (об этом ниже).
Вектор r₁' и угол α₁ относятся к положению источника в запаздывающий, нулевой момент времени, тогда как давление p₁ и сила ΔF₁ определяются в момент времени t₁. За время t₁, пока волна проходила расстояние r₁’ до точки Q₁, источник сместился по оси х на расстояние vt₁ = βr₁’ от начала координат. Обозначим расстояние от источника S(vt₁, 0, 0) до точки Q₁ (x₁, y₁, z₁) как r₁:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
Далее обозначим
u₁ = x₁ – vt₁ = x₁ – βr₁’.
Давайте перепишем уравнения для p₁ и ΔF₁ в точке Q₁ относительно r₁, u₁, y₁, и z₁, вместо r₁’, x₁, y₁, и z₁, то есть относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Воспользуемся уравнением:
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁² ,
Раскрыв скобки и перенеся все налево, мы можем выразить r₁' через u₁, y₁, z₁ и β путем решения квадратного уравнения
(1 – β²) r₁’² – 2 β u₁ r₁’ – (u₁² + y₁² + z₁²) = 0
Получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
Давление в точке Q₁ тогда равно:
p₁ = pₐa/r₁’ = pₐa (1 – β²) / (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)
Так же мы можем выразить ΔF₁ (в скалярной форме) через u₁, y₁, z₁ и β:
cos α₁ = x₁ / r₁'
А поскольку x₁ = u₁ + βr₁’ , то
cos α₁ = β + u₁ / r₁’
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
ΔF₁ = pₐa / (r₁’² (1 – β cos α₁)) ΔxΔyΔz =
= pₐa / ((β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
В векторной форме, ΔF₁ нужно умножить на единичный вектор в направлении r₁':
ΔF₁ = ΔF₁ r₁'/r₁' = ΔF (r₁ + vt₁) / |r₁ + vt₁| = pₐa (r₁ + vt₁) / (|r₁ + vt₁| (β u₁ / (1 – β²)½ + (u₁² / (1 – β²) + y₁² + z₁²)½) (u₁² / (1 – β²) + y₁² + z₁²)½) ΔxΔyΔz
Получилось довольно громоздкое выражение. Однако, все эти x₁, y₁, z₁, u₁, t₁ – не переменные, а фиксированные значения. Они относятся только к одной единичной волне, к одному моменту времени и к трем точкам (начало координат О, положение источника в момент t₁ и точка Q₁). Как будут выглядеть уравнения для p и ΔF для разных моментов времени, где x, y, z, u, t – это переменные, а не фиксированные значения?
Проведем прямую линию от положения источника в момент времени t₁ (точка S) к точке Q₁ (первая единичная волна из начала координат достигает ее также в момент t₁). Попробуем определить, чему равны давление p и сила ΔF в момент t₁ в других точках прямой SQ₁. Введем переменные при помощи переменного коэффициента ω:
u = ω u₁
Из вышеприведенного рисунка (где нарисованы первая и вторая единичные волны, точки О, S, Q₁ и Q₂) видно, что тогда остальные переменные, относящиеся к этой прямой и к моменту t₁, тоже можно выразить через ω (ω₁, ω₂, ω₃ – разные значения):
y = ω y₁ z = ω z₁ r = ω r₁
Давление в произвольной точке Q(u, y, z) будет равно
p = p₁ / ω = pₐa (1 – β²) / (ω (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½)) =
= pₐa (1 – β²) / (ω (β u/ω + ((u/ω)² + (1 – β²) ((y/ω)² + (z/ω)²))½)) =
= pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
Аналогично, для силы мы получим
ΔF = pₐa / ((β u / (1 – β²)½ + (u² / (1 – β²) + y² + z²)½) (u² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Очень хорошо, мы избавились от ω и оказалось, что для переменных x, y, z, u это уравнение выглядит точно так же, как и для фиксированных значений x₁, y₁, z₁, u₁. А поскольку угол α₁ в первоначальном уравнении мог быть произвольным и он определялся соотношением между x₁ и r₁’, то уравнения для p и ΔF справедливы не только для прямой SQ₁, но во всем пространстве. Заметим, что время t₁ или t в этих уравнениях вообще не фигурирует, потому что они записаны для системы отсчета источника, и здесь на место одной единичной волны сразу же приходит другая, с теми же значениями p и ΔF (см. выше об источнике в СО покоящейся среды и аналогии с электростатикой).
Однако время, безусловно, должно фигурировать в уравнениях для СО покоящейся среды. Давайте совершим обратный переход в эту СО. Заменим
u = x – vt
где vt – это положение источника в момент t.
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½) =
= pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
ΔF = pₐa / ((β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
ΔF = pₐa (r + vt) / (|r + vt| (β (x – vt) / (1 – β²)½ + ((x – vt)² / (1 – β²) + y² + z²)½) ((x – vt)² / (1 – β²) + y² + z²)½) ΔxΔyΔz
Читатель, конечно, уже обратил внимание, что здесь «напрашивается» та же самая замена, что и в преобразовани Лоренца для координаты:
x' = (x – vt)/(1 – β²)½ = γ (x – vt)
Да, уравнения для p и ΔF при этом немного упростятся:
p = pₐa / (γ (β x' + (x'² + y² + z²)½)
ΔF = pₐa / ((β x' + (x'² + y² + z²)½) (x'² + y² + z²)½) ΔxΔyΔz
Ну и что? Что это нам дает? Абсолютно ничего. А вот на что следует обратить особое внимание, это на то, что уравнения в СО покоящейся среды и в СО источника выглядят совершенно одинаково по форме и переход между ними осуществляется согласно преобразованию Галилея:
p = pₐa (1 – β²) / (β u + (u² + (1 – β²) (y² + z²))½)
↓
p = pₐa (1 – β²) / (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½)
Уравнения для ΔF в разных системах отсчета выглядят тоже одинаково. В уравнениях в обеих СО, есть и (1 – β²), и β, и корень квадратный – в одинаковых местах. Более того, для вывода этих уравнений нам понадобилось перейти из СО покоящейся среды в СО источника при помощи преобразования Галилея, а потом обратно.
Между прочим, обратите внимание, что эти уравнения вовсе не описывают распространение сферических волн со скоростью c. Они описывают эквипотенциальные поверхности, которые, хотя и совпадают с мгновенным снимком фронтов волн, в отличие от последних, «заморожены» относительно источника. В СО источника, эквипотенциальные поверхности неподвижны. В СО покоящейся среды, они двигаются вместе с источником, с той же скоростью v. Как я уже говорил, это происходит потому, что на место одной единичной волны с определенными значениями p и ΔF тут же приходит другая волна, с теми же значениями. Это не статика в том смысле, что никакого движения нет; это динамическое равновесие.
Что касается фронтов волн, то они двигаются и в СО источника. Выведем формулу их распространения.
В СО покоящейся среды, фронты волн распространяются по формуле:
(x – ξ)² + y² + z² = c²(t – ԏ)²
где ξ – координата источника по оси x в момент времени ԏ, когда была излучена соответствующая единичная волна. Если источник движется с постоянной скоростью v, то ξ = vԏ.
При переходе в СО источника, мы должны воспользоваться преобразованием Галилея
u = x – vt или x = u + vt
Получим
(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²
Чтобы смысл этого уравнения был более понятен, запишем его немного по-другому, через единичные волны. Пусть первая единичная волна была излучена в момент dt (а не в нулевой, как я раньше писал; сейчас я меняю нумерацию ради получения более простого уравнения, чтобы там не было i -1), вторая – в момент 2 dt, третья – в момент 3 dt, а i-ая – в момент i dt. Тогда уравнение распространения i-ой волны можно записать как
(x – v i dt)² + y² + z² = c² (t – i dt)²
где ԏ = i dt, ξ(ԏ) = v i dt.
Перейдем в СО источника, произведя замену x = u + v t:
(u + v (t – i dt))² + y² + z² = c² (t – i dt)²
Это уравнение, действительно, описывает те самые сферические единичные волны, распространяющиеся со скоростью c и «сдуваемые» встречным ветром со скоростью –v. Так что описание волн давления в обеих СО выглядит полностью аналогичным. Галилей рулит.
Напомню еще раз, что всё это относится к упрощенному случаю очень большой длины волны, где мы можем считать, что давление на поверхности источника pₐ ≈ const, причем pₐ > 0. Пара слов о случае, когда pₐ < 0 и при этом pₐ ≈ const. Здесь просто зеркальное отражение случая pₐ > 0. Вся разница в том, что силовые линии направлены не от источника, а к источнику. Все остальное то же самое – силовые линии искривляются точно так же, все формулы просто меняют знаки плюс на минус и наоборот.
В случае переменного давления, когда pₐ более не константа и постоянно меняет знак, формулы для звукового давления p и силы ΔF более выполняться не будут, они будут иметь более сложный характер. На каком-то участке волны сила ΔF будет направлена от источника, на другом участке – к источнику (точнее, к той точке, где был источник в момент излучения данной единичной волны).
Но что важно: силовые линии останутся теми же самыми, искривленными точно так же (хотя на каждой силовой линии ΔF будет многократно менять знак и величину). Потому что фронты волн давления, совпадающие с эквипотенциальными поверхностями, будут распространяться точно так же, а сила перпендикулярна эквипотенциальным поверхностям.
Отредактировано: Yuri Rus - 02 дек 2019 03:33:35
ОТВЕТЫ (2)
|
|
Поверонов ( Слушатель ) |
| 28 май 2011 12:49:50 |
Цитата: Yuri Rus от 24.05.2011 07:54:00
Очевидно имеется в виду точка Q1 с чертежа, а не P₁.
Цитата: Yuri Rus от 24.05.2011 07:54:00
Понял насчет α₁. Вопрос отпал.
|
|
Yuri Rus ( Слушатель ) |
| 28 май 2011 16:57:48 |
Цитата: Поверонов от 28.05.2011 12:49:50
Спасибо, исправил.
Цитата: Поверонов от 28.05.2011 12:49:50
Я не знаю, в чем был вопрос. Вообще говоря, для второй единичной волны угол был бы α₂, а не α₁, но эти углы практически одинаковые, поскольку vdt << r₁’. Потому при выводе, скажем, уравнения Доплера для частоты звука (этот вывод полностью аналогичен моему выводу для Δp₁/Δr₁’) различием этих углов пренебрегают.
P.S. Вы меня заинтриговали интерференцией новой и запаздывающей волн (собственно, я понял Вас так, что Вы говорите про две последовательные волны, слово "запаздывающая волна" имеет другой смысл; если же речь идет не о последовательных волнах, то я Вас вообще не понял). Вот именно что я буду много говорить о взаимодействии последовательных волн, но я пользуюсь совсем другой терминологией и, видимо, другими литературными источниками (гидродинамика, сверхзвуковые явления и пр.). Не могли бы Вы дать мне ссылки на то, что Вы имели в виду?