Были или нет американцы на Луне?
13,622,050
111,032
|
|
Vesper ( Слушатель ) |
| 15 апр 2019 в 05:32 |
Наличие атмосферы в лунной миссии Apollo 16
новая дискуссия Статья 1.839
В связи с объявлением новой лунной программы в интернет-сообществе вновь оживился спор о том, была ли реализована первая лунная программа Аполлон. Среди множества аргументов pro et contra я недавно встретил попытку проанализировать известный видеоролик о движении ровера по «лунной» поверхности https://glav.su/forum/1/682/messages/5122059/#message5122059 . Параметром для анализа являлась высота подбрасываемого колесами песка, которая достигает примерно 1.5 метра. Если видео не было искусственно замедлено, скорость ровера получается примерно 2.8 м/с, и тогда подобная высота подъема песка на Земле с ускорением g = 9.8 м/с не достижима. Однако, замедлить скорость видео несложно, поэтому подобный анализ ничего не доказывает.
На видео видно, что песок во время движения ровера вылетает разлетающимися кольцами, форма которых долго сохраняется. Я попробовал проанализировать динамику этих колец, чтобы решить вопрос о возможном наличии атмосферы в этих съемках. Хорошо известно, что трение при невысоких скоростях пропорционально скорости движения тела, поэтому траектория движения отличается от параболы, которая должна наблюдаться в отсутствие атмосферы. Траекторию движения легко определить по видео. Кроме того, есть еще один характерный момент. Скорость захваченных колесом частиц несколько варьирует, поэтому в отсутствие атмосферы быстрые частицы будут улететь дальше, а медленные отставать, так что «фронт» волны будет линейно расплываться со временем. Однако, в присутствии атмосферы быстрые частицы будут тормозиться сильнее, а медленные слабее. Кроме того, быстрые частицы, летящие первыми, захватывают с собою воздушный поток, который также облегчает движение последующих более медленных частиц. В результате фронт волны долго остается резким, и начинает расплываться только в самом конце, когда движение полностью тормозиться. По этим двум признакам можно надежно определить наличие атмосферы.
На ролике https://youtu.be/8lERB9BPzC4 были выбраны кадры 1438-1470 (0:47 мин), их анализ я проводил в программе Matlab. Для каждого кадра были проведены вручную маркерные линии по характерным деталям рельефа (синие линии), которые служили осями координат. Для учета зума (он менялся в ходе съемок) была проведена вторая (фиолетовая) линия. Самое большое кольцо песка аппроксимировалось дугой окружности (желтая линия), координаты ее левого верхнего края анализировались.



Чтобы увеличить резкость, эту часть кадра я анализировал отдельно в небольшом квадрате размерном 201*201 пиксель. В этом квадрате строилось распределение плотности частиц по вертикальной и горизонтальной осям.



Масштаб в метрах определялся по диаметру колеса ровера, который равен 0.81 м.
На этом рисунке показан результат.
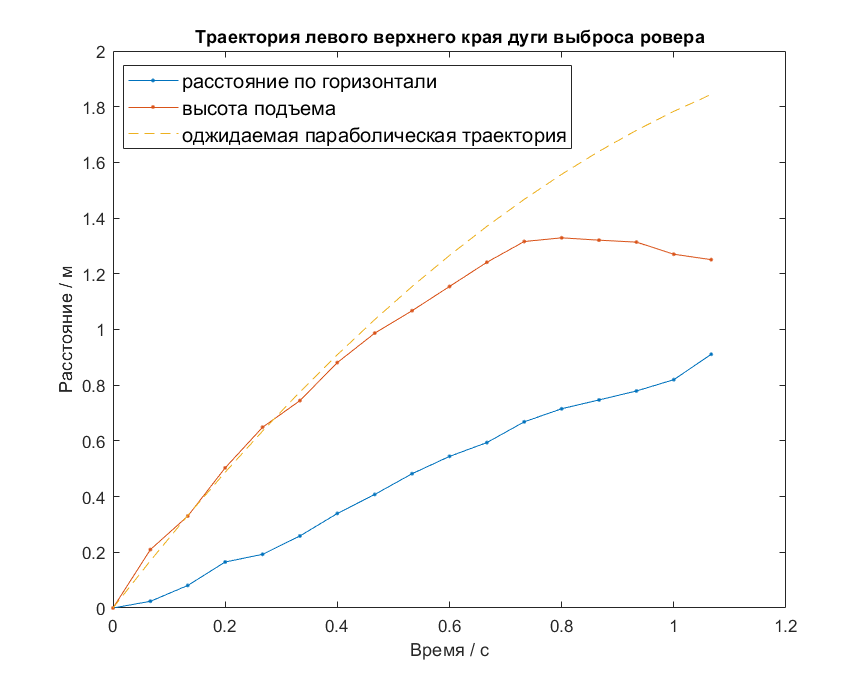
Таким образом, наличие атмосферы в миссии Apollo 16 является экспериментальным фактом.
Для желающих посмотреть профиль фронта (распределение плотности) на разных кадрах привожу код, исходные файлы вышлю по запросу, так как разместить их здесь не удается.
==============================================================
clear
clc
fname = 'videoplayback_mp4_01438_input.tif'; % original file
fname1 = 'videoplayback_mp4_01438_output.png'; % + coordinates markers
fname2 = 'videoplayback_mp4_01438_output_short.png'; % X-Y positions
nn = 1438:2:1470; % analyzed frames numbers
X = zeros(1,17);
Y = zeros(1,17);
T = 2*(0:16)/30;
for n = 1:17 % only 17 frames are used
fname(20:23) = num2str(nn(n),'%4i');
fname1(20:23) = num2str(nn(n),'%4i');
fname2(20:23) = num2str(nn(n),'%4i');
A = imread(fname);
B = A;
y0 = 630; % Y marker position (fixed for all frames)
n0 = 100; % size of the small probe square for precise analysis
sc1 = 0.81/128; % scaling factor m/pixel
xx = 105; % scaling factor for changing zoom
disp(nn(n))
switch nn(n)
case 1438
x0 = 1200 ; % X0 marker position
x1 = 1302 ; % X1 marker position
xc = x0-78; % X center of circle
yc = y0-90; % Y center of circle
f1 = -70; % low angle of arc
f2 = -10; % hig angle of arc
rr = 75; % circle radius
x9 = -2; % X correction for the left arc edge
y9 = 14; % Y correction for the left arc edge
case 1440
x0 = 1215 ;
x1 = 1320 ;
xc = x0-81;
yc = y0-93;
f1 = -65;
f2 = +14;
rr = 75;
x9 = -2;
y9 = 14;
case 1442
x0 = 1235 ;
x1 = 1340 ;
xc = x0-81;
yc = y0-95;
f1 = -45;
f2 = +25;
rr = 75;
x9 = -6;
y9 = 10;
case 1444
x0 = 1255 ;
x1 = 1359 ;
xc = x0-84;
yc = y0-95;
f1 = -40;
f2 = +45;
rr = 75;
x9 = -2;
y9 = 6;
case 1446
x0 = 1273 ;
x1 = 1379 ;
xc = x0-88;
yc = y0-108;
rr = 77;
f1 = -40;
f2 = +60;
x9 = +12;
y9 = 6;
case 1448
x0 = 1290 ;
x1 = 1397 ;
xc = x0-95;
yc = y0-115;
rr = 95;
f1 = -50;
f2 = +65;
x9 = +6;
y9 = 16;
case 1450
x0 = 1308 ;
x1 = 1415 ;
xc = x0-105;
yc = y0-127;
rr = 105;
f1 = -45;
f2 = +70;
x9 = 8;
y9 = 18;
case 1452
x0 = 1329 ;
x1 = 1436 ;
xc = x0-115;
yc = y0-130;
rr = 113;
f1 = -45;
f2 = +70;
x9 = +4;
y9 = 12;
case 1454
x0 = 1349 ;
x1 = 1456 ;
xc = x0-125;
yc = y0-135;
rr = 125;
f1 = -45;
f2 = +75;
x9 = 8;
y9 = 18;
case 1456
x0 = 1370 ;
x1 = 1477 ;
xc = x0-130;
yc = y0-142;
rr = 130;
f1 = -45;
f2 = +78;
x9 = 8;
y9 = 18;
case 1458
x0 = 1391 ;
x1 = 1498 ;
xc = x0-137;
yc = y0-149;
rr = 137;
f1 = -45;
f2 = +78;
x9 = 6;
y9 = 18;
case 1460
x0 = 1414 ;
x1 = 1521 ;
xc = x0-144;
yc = y0-150;
rr = 144;
f1 = -45;
f2 = +80;
x9 = 4;
y9 = 14;
case 1462
x0 = 1436 ;
x1 = 1546 ;
xc = x0-151;
yc = y0-150;
rr = 153;
f1 = -45;
f2 = +82;
x9 = 4;
y9 = 14;
case 1464
x0 = 1460 ;
x1 = 1574 ;
xc = x0-158;
yc = y0-150;
rr = 162;
f1 = -45;
f2 = +82;
x9 = 0;
y9 = 14;
case 1466
x0 = 1486 ;
x1 = 1602 ;
xc = x0-165;
yc = y0-150;
rr = 170;
f1 = -45;
f2 = +82;
x9 = -2;
y9 = 18;
case 1468
x0 = 1512 ;
x1 = 1631 ;
xc = x0-172;
yc = y0-150;
rr = 170;
f1 = -45;
f2 = +82;
x9 = -6;
y9 = 18;
case 1470
x0 = 1542 ;
x1 = 1658 ;
xc = x0-172;
yc = y0-144;
rr = 170;
f1 = -45;
f2 = +84;
x9 = -12;
y9 = 24;
otherwise
disp('other value')
end
% arc positions
for i=f1:f2
ix = floor(+rr*cos(pi*i/180) + xc);
iy = floor(-rr*sin(pi*i/180) + yc);
A(iy,ix,1:2) = 255;
end
% radius positions
for j=0:rr
jx = floor(+j*cos(pi*f1/180) + xc);
jy = floor(-j*sin(pi*f1/180) + yc);
A(jy,jx,1:2) = 255;
end
A(:,x0,1) = 0;
A(:,x1,2) = 0;
A(y0,:,1) = 0;
% coordinates of the arc left edge
X(n) = (ix + x9 - x0)*sc1*xx/(x1-x0);
Y(n) = (iy + y9 - y0)*sc1*xx/(x1-x0);
% probe square for precise analysis
C = B(iy-n0:iy+n0,ix-n0:ix+n0,:);
max1 = max(max(C(:,:,1))); min1 = min(min(C(:,:,1)));
max2 = max(max(C(:,:,2))); min2 = min(min(C(:,:,2)));
max3 = max(max(C(:,:,3))); min3 = min(min(C(:,:,3)));
D = C;
D(:,:,1) = (C(:,:,1)-min1)*(255/(max1-min1));
D(:,:,2) = (C(:,:,2)-min2)*(255/(max2-min2));
D(:,:,3) = (C(:,:,3)-min3)*(255/(max3-min3));
D(:,n0+x9,1:1) = 255;
D(n0+y9,:,2:2) = 255;
% dust density
L = -n0:n0;
P1 = mean(squeeze(D(n0+y9,:,1:3)),2);
P2 = mean(squeeze(D(:,n0+x9,1:3)),2);
figure(1)
subplot(1,2,1)
image(C)
subplot(1,2,2)
image(D)
figure(2)
image(A)
figure(3)
plot(L,P1,L,P2)
pause
% imwrite(A,fname1)
% imwrite(D,fname2)
end
%%
X = X(1)-X;
Y = Y(1)-Y;
%%
T1 = T;
G = 9.8 / 6;
V0 = 2.6;
Z = V0*T1 - 0.5*G*T1.^2;
figure(4)
plot(T1,X,'.-',T1,Y,'.-',T1,Z,'--')
% xlim([500 600])
% title('Synechococcus (DDM) 740 nm')
% title('Synechocystis T = 279 K Orth')
title('Траектория левого верхнего края дуги выброса ровера')
xlabel('Время / с'); ylabel('Расстояние / м');
legend('расстояние по горизонтали','высота подъема','оджидаемая параболическая траектория','Location','best','fontsize',12)
На видео видно, что песок во время движения ровера вылетает разлетающимися кольцами, форма которых долго сохраняется. Я попробовал проанализировать динамику этих колец, чтобы решить вопрос о возможном наличии атмосферы в этих съемках. Хорошо известно, что трение при невысоких скоростях пропорционально скорости движения тела, поэтому траектория движения отличается от параболы, которая должна наблюдаться в отсутствие атмосферы. Траекторию движения легко определить по видео. Кроме того, есть еще один характерный момент. Скорость захваченных колесом частиц несколько варьирует, поэтому в отсутствие атмосферы быстрые частицы будут улететь дальше, а медленные отставать, так что «фронт» волны будет линейно расплываться со временем. Однако, в присутствии атмосферы быстрые частицы будут тормозиться сильнее, а медленные слабее. Кроме того, быстрые частицы, летящие первыми, захватывают с собою воздушный поток, который также облегчает движение последующих более медленных частиц. В результате фронт волны долго остается резким, и начинает расплываться только в самом конце, когда движение полностью тормозиться. По этим двум признакам можно надежно определить наличие атмосферы.
На ролике https://youtu.be/8lERB9BPzC4 были выбраны кадры 1438-1470 (0:47 мин), их анализ я проводил в программе Matlab. Для каждого кадра были проведены вручную маркерные линии по характерным деталям рельефа (синие линии), которые служили осями координат. Для учета зума (он менялся в ходе съемок) была проведена вторая (фиолетовая) линия. Самое большое кольцо песка аппроксимировалось дугой окружности (желтая линия), координаты ее левого верхнего края анализировались.



Чтобы увеличить резкость, эту часть кадра я анализировал отдельно в небольшом квадрате размерном 201*201 пиксель. В этом квадрате строилось распределение плотности частиц по вертикальной и горизонтальной осям.



Масштаб в метрах определялся по диаметру колеса ровера, который равен 0.81 м.
На этом рисунке показан результат.

Таким образом, наличие атмосферы в миссии Apollo 16 является экспериментальным фактом.
Для желающих посмотреть профиль фронта (распределение плотности) на разных кадрах привожу код, исходные файлы вышлю по запросу, так как разместить их здесь не удается.
==============================================================
clear
clc
fname = 'videoplayback_mp4_01438_input.tif'; % original file
fname1 = 'videoplayback_mp4_01438_output.png'; % + coordinates markers
fname2 = 'videoplayback_mp4_01438_output_short.png'; % X-Y positions
nn = 1438:2:1470; % analyzed frames numbers
X = zeros(1,17);
Y = zeros(1,17);
T = 2*(0:16)/30;
for n = 1:17 % only 17 frames are used
fname(20:23) = num2str(nn(n),'%4i');
fname1(20:23) = num2str(nn(n),'%4i');
fname2(20:23) = num2str(nn(n),'%4i');
A = imread(fname);
B = A;
y0 = 630; % Y marker position (fixed for all frames)
n0 = 100; % size of the small probe square for precise analysis
sc1 = 0.81/128; % scaling factor m/pixel
xx = 105; % scaling factor for changing zoom
disp(nn(n))
switch nn(n)
case 1438
x0 = 1200 ; % X0 marker position
x1 = 1302 ; % X1 marker position
xc = x0-78; % X center of circle
yc = y0-90; % Y center of circle
f1 = -70; % low angle of arc
f2 = -10; % hig angle of arc
rr = 75; % circle radius
x9 = -2; % X correction for the left arc edge
y9 = 14; % Y correction for the left arc edge
case 1440
x0 = 1215 ;
x1 = 1320 ;
xc = x0-81;
yc = y0-93;
f1 = -65;
f2 = +14;
rr = 75;
x9 = -2;
y9 = 14;
case 1442
x0 = 1235 ;
x1 = 1340 ;
xc = x0-81;
yc = y0-95;
f1 = -45;
f2 = +25;
rr = 75;
x9 = -6;
y9 = 10;
case 1444
x0 = 1255 ;
x1 = 1359 ;
xc = x0-84;
yc = y0-95;
f1 = -40;
f2 = +45;
rr = 75;
x9 = -2;
y9 = 6;
case 1446
x0 = 1273 ;
x1 = 1379 ;
xc = x0-88;
yc = y0-108;
rr = 77;
f1 = -40;
f2 = +60;
x9 = +12;
y9 = 6;
case 1448
x0 = 1290 ;
x1 = 1397 ;
xc = x0-95;
yc = y0-115;
rr = 95;
f1 = -50;
f2 = +65;
x9 = +6;
y9 = 16;
case 1450
x0 = 1308 ;
x1 = 1415 ;
xc = x0-105;
yc = y0-127;
rr = 105;
f1 = -45;
f2 = +70;
x9 = 8;
y9 = 18;
case 1452
x0 = 1329 ;
x1 = 1436 ;
xc = x0-115;
yc = y0-130;
rr = 113;
f1 = -45;
f2 = +70;
x9 = +4;
y9 = 12;
case 1454
x0 = 1349 ;
x1 = 1456 ;
xc = x0-125;
yc = y0-135;
rr = 125;
f1 = -45;
f2 = +75;
x9 = 8;
y9 = 18;
case 1456
x0 = 1370 ;
x1 = 1477 ;
xc = x0-130;
yc = y0-142;
rr = 130;
f1 = -45;
f2 = +78;
x9 = 8;
y9 = 18;
case 1458
x0 = 1391 ;
x1 = 1498 ;
xc = x0-137;
yc = y0-149;
rr = 137;
f1 = -45;
f2 = +78;
x9 = 6;
y9 = 18;
case 1460
x0 = 1414 ;
x1 = 1521 ;
xc = x0-144;
yc = y0-150;
rr = 144;
f1 = -45;
f2 = +80;
x9 = 4;
y9 = 14;
case 1462
x0 = 1436 ;
x1 = 1546 ;
xc = x0-151;
yc = y0-150;
rr = 153;
f1 = -45;
f2 = +82;
x9 = 4;
y9 = 14;
case 1464
x0 = 1460 ;
x1 = 1574 ;
xc = x0-158;
yc = y0-150;
rr = 162;
f1 = -45;
f2 = +82;
x9 = 0;
y9 = 14;
case 1466
x0 = 1486 ;
x1 = 1602 ;
xc = x0-165;
yc = y0-150;
rr = 170;
f1 = -45;
f2 = +82;
x9 = -2;
y9 = 18;
case 1468
x0 = 1512 ;
x1 = 1631 ;
xc = x0-172;
yc = y0-150;
rr = 170;
f1 = -45;
f2 = +82;
x9 = -6;
y9 = 18;
case 1470
x0 = 1542 ;
x1 = 1658 ;
xc = x0-172;
yc = y0-144;
rr = 170;
f1 = -45;
f2 = +84;
x9 = -12;
y9 = 24;
otherwise
disp('other value')
end
% arc positions
for i=f1:f2
ix = floor(+rr*cos(pi*i/180) + xc);
iy = floor(-rr*sin(pi*i/180) + yc);
A(iy,ix,1:2) = 255;
end
% radius positions
for j=0:rr
jx = floor(+j*cos(pi*f1/180) + xc);
jy = floor(-j*sin(pi*f1/180) + yc);
A(jy,jx,1:2) = 255;
end
A(:,x0,1) = 0;
A(:,x1,2) = 0;
A(y0,:,1) = 0;
% coordinates of the arc left edge
X(n) = (ix + x9 - x0)*sc1*xx/(x1-x0);
Y(n) = (iy + y9 - y0)*sc1*xx/(x1-x0);
% probe square for precise analysis
C = B(iy-n0:iy+n0,ix-n0:ix+n0,:);
max1 = max(max(C(:,:,1))); min1 = min(min(C(:,:,1)));
max2 = max(max(C(:,:,2))); min2 = min(min(C(:,:,2)));
max3 = max(max(C(:,:,3))); min3 = min(min(C(:,:,3)));
D = C;
D(:,:,1) = (C(:,:,1)-min1)*(255/(max1-min1));
D(:,:,2) = (C(:,:,2)-min2)*(255/(max2-min2));
D(:,:,3) = (C(:,:,3)-min3)*(255/(max3-min3));
D(:,n0+x9,1:1) = 255;
D(n0+y9,:,2:2) = 255;
% dust density
L = -n0:n0;
P1 = mean(squeeze(D(n0+y9,:,1:3)),2);
P2 = mean(squeeze(D(:,n0+x9,1:3)),2);
figure(1)
subplot(1,2,1)
image(C)
subplot(1,2,2)
image(D)
figure(2)
image(A)
figure(3)
plot(L,P1,L,P2)
pause
% imwrite(A,fname1)
% imwrite(D,fname2)
end
%%
X = X(1)-X;
Y = Y(1)-Y;
%%
T1 = T;
G = 9.8 / 6;
V0 = 2.6;
Z = V0*T1 - 0.5*G*T1.^2;
figure(4)
plot(T1,X,'.-',T1,Y,'.-',T1,Z,'--')
% xlim([500 600])
% title('Synechococcus (DDM) 740 nm')
% title('Synechocystis T = 279 K Orth')
title('Траектория левого верхнего края дуги выброса ровера')
xlabel('Время / с'); ylabel('Расстояние / м');
legend('расстояние по горизонтали','высота подъема','оджидаемая параболическая траектория','Location','best','fontsize',12)
Отредактировано: Vesper - 19 апр 2019 в 09:59
X
15 апр 2019 18:56Предупреждение от модератора ДядяВася:
Код под спойлер уберите
ОТВЕТЫ (17)
|
|
Bashir_Petrov ( Слушатель ) |
| 16 апр 2019 в 05:03 |
Всё таки, кажется, пыль слишком быстро оседает. При наличии атмосферы облака мелкой пыли висят дольше, но это, конечно, субъективное ощущение. 

|
|
Ксан_Доф ( Слушатель ) |
| 16 апр 2019 в 08:14 |
Необходимо всё же учитывать характер "пыли". Также, нет достоверных съёмок о оседании пыли в условиях космоса (только теории).
|
|
ДальнийВ ( Слушатель ) |
| 16 апр 2019 в 11:42 |
Цитата: Vesper от 15.04.2019 05:32:18
Есть ещё очень интересная странность наблюдаемого выброса "реголита" из под колеса - этот "реголит" представляет собой необычайно однородную фракцию. Что не соответствует образцам грунта доставленных с Луны советскими автоматами.
Вывод - мы наблюдаем рукотворный "реголит".
|
|
Luddit ( Слушатель ) |
| 16 апр 2019 в 12:45 |
Цитата: ДальнийВ от 16.04.2019 11:42:15
Без натурной проверки аргумент не очень. Может быть именно эту фракцию сетчатые колеса могли захватить и отправить в полет.
|
|
ДальнийВ ( Слушатель ) |
| 16 апр 2019 в 14:12 |
Цитата: Luddit от 16.04.2019 12:45:28
А чем вам другое небесное тело не подходит?
К тому-же поглядите на ближний план, поверхность ну точь в точь как лунная.
Конечно, можно принять за аксиому что на поверхности Луны нет ни одного камешка, то тогда понятно.
.
Фото возможно неудачное, но можно найти море других, где прекрасно видны крупные фракции.
|
|
Митрофан ( Слушатель ) |
| 17 апр 2019 в 11:52 |
Цитата: Vesper от 15.04.2019 05:32:18
Спасибо Вам за проделанную работу. Было очень интересно почитать.
|
|
Technik ( Слушатель ) |
| 19 апр 2019 в 17:10 |
Цитата: Vesper от 15.04.2019 05:32:18
Вашу бы энергию и ваши знания да – как говорится – в мирных бы целях. А так – получилась подгонка результатов анализа под заранее сформулированный вывод – «Таким образом, наличие атмосферы в миссии Apollo 16 является экспериментальным фактом».
Я, например, в этом самом ролике вполне себе наблюдаю моменты, когда выбрасываемый колесами ровера реголит летит вполне себе по параболе. Словом, неинтересно…
Заинтересовало другое, ваше «Однако, замедлить скорость видео несложно, поэтому подобный анализ ничего не доказывает». Одно это утверждение уже выдает вас - несмотря на ваш уровень как программиста – как стандартного опроверга. Готового принять на веру любые, вплоть до самых невменяемых, утверждения, обосновывающие «аферу».
Вообще-то - доказывает, но во все времена действует не помню уж кем
 сформулированная максима – «"Не существовало, не существует и не будет существовать аргументов, способных убедить сторонников "аферы" в обратном" ©
сформулированная максима – «"Не существовало, не существует и не будет существовать аргументов, способных убедить сторонников "аферы" в обратном" ©Мой расчет дал величину выброса реголита – при принятой для расчета модели! – 1, 47 метра. Что достаточно точно совпало с наблюдаемой в ходе исследуемого фрагмента ролика реальной высотой – в среднем примерно 1,6 метра.
Возник вопрос – а с какой скоростью должен ехать ровер на Земле, чтобы грунт выбрасывался на эти самые 1,47 метров?
Из ранее выведенной формулы
H = h + [ (2 π R / Т) × sin 50°]2 : 2a.
определим период вращения колеса ровера Т, при высоте Н = 1, 47 и h = 0,14 метра, для ускорения свободного падения а = g = 9,81 м/сек2 - получаем, что Т = 0,38 сек.
Что (согласно V = 2 π R/Т) дает скорость движения ровера на Земле, равную 6,7 м/сек, или 24 км/час.
Не знаю, каков у вас опыт вождения, но мой говорит о том, что при езде по показанному в ролике на дальнем плане рельефу даже с такой скоростью (а в ролике есть моменты, когда ровер едет значительно быстрее, чем в отрезке, взятом мною для определения скорости) – ровер на этих ухабах поломался бы к едрене фене, а пассажира просто выкинуло бы с сиденья, и никакие липучки ему не помогли бы.
Так что ваш труд насмарку. Меня вы не убедили, а для ваших коллег-опровергов не стоило так стараться – они и без вас твердо уверены, что никаких высадок не было.
|
|
Vesper ( Слушатель ) |
| 22 апр 2019 в 01:17 |
Цитата: Technik от 19.04.2019 17:10:33
Видимо, вам это трудно понять, но мне было просто интересно разобраться, и поэтому не жаль провести одну ночь за этими, в общем-то достаточно простыми расчетами, которые не выходят за рамки школьной физики. Если нашли в них ошибку - буду искренне признателен.
Цитата: Technik от 19.04.2019 17:10:33
Будьте уж так любезны - покажите эту параболу
Цитата: Technik от 19.04.2019 17:10:33
Довольно опрометчиво делать выводы о человеке по одному безымянному посту. Такое скоропалительное суждение вас ведь тоже характеризует вполне определенным образом.
Цитата: Technik от 19.04.2019 17:10:33
Я не знаком ни с теми, ни с другими, случайно наткнулся на этот ролик, показалось занятным. Поскольку внятного ответа не получил, решил разобраться сам. Результаты тиснул на форум. Все.
Цитата: Technik от 19.04.2019 17:10:33
Это безусловно сильная аргументация, но я не разбираюсь в конструкции багги и могу только довериться вашей технической интуиции.
Цитата: Technik от 19.04.2019 17:10:33
Простите, что занял ваше время.
|
|
Technik ( Слушатель ) |
| 23 апр 2019 в 19:46 |
Цитата: Vesper от 22.04.2019 01:17:13
В данном случае, применительно к вашему отношению к лунной программе, увы, не очень опрометчиво. Просто - извините за выражение - вменяемый (опять же оговорюсь - в плане отношения к лунной программе) человек, придя в своих расчетах, оценках к вашему выводу - "Таким образом, наличие атмосферы в миссии Apollo 16 является экспериментальным фактом" - не будет его публиковать, а будет искать, в чем же он ошибся.
Кстати, я специально легонько сжульничал, заявляя, что пассажира выкинуло бы с сиденья. На ровере, кроме липучек, фиксирующих спину астронавта, есть и привязной ремень, фиксирующий бедра. И хотя разговор об этом был вот только что, ни Вы, ни ваши коллеги-опроверги на это не обратили внимания. Что очень неплохо иллюстрирует их отношение к деталям - за исключением тех, что "доказывают аферу".
Тем не менее на такой скорости на таком рельефе на Земле пассажира мотало бы на сиденье ровера на грани травмирования. Что совсем не наблюдается в ролике.
|
|
Technik ( Слушатель ) |
| 23 апр 2019 в 21:00 |
Цитата: ДядяВася от 23.04.2019 20:35:10
Это вы меня обижаешь. Потому что столь невнимательно относитесь к такому виднейшему персонажу сообщества Авантюры, как я, что не знаете, что в 2013-м меня здесь в помине не было (и до сих пор не было бы, если достославный Ираквар не был бы убит), а так глыбОко я в ветку не погружался.
Но и в те далекие времена вы, опроверги, как всегда, были весьма, миль пардон, малоэрудированы. Потому что, во-первых, гордо упрекали астронавта, что он сидит как приклеенный к креслу - а он действительно приклеен, и этим фактом я только что утер нос вашему сообществу, и во-вторых, малость нажульничали, приписав роверу вставание на дыбы как мустангу. Чего в ролике в помине нет.
Я сегодня добрый, так что можете считать, что я вас за нанесенную мне обиду простил. Спокойной ночи, и не забудьте ответить на поставленные мной несколько выше вопросы.
|
|
ДядяВася ( Слушатель ) |
| 23 апр 2019 в 21:29 |
Цитата: Technik от 23.04.2019 21:00:27
Это не оправдывает Вашего незнания. Сначала изучите, что достопочтенные доны за и против написали.
Цитата: Technik от 23.04.2019 21:00:27
Да не тянет это на разумное техническое решение, потому и нигде и никогда не применяется, кроме как для игрушек.
Объясняю. Если используется ремень, то ты точно знаешь, что он держит, и внезапно не "оборвётся" и ты не полетишь носом вперёд.
В случае липучки, то при превышении нагрузки (а когда она превысит тебе неизвестно), при наезде на бугор или при торможении (местность пересечённая) ты летишь вперёд. Вылететь с тележки ты не вылетешь (ремень на окорочках не позволит), но или пульт или гермошлем (что крепче?) ты расшибёшь. А нос, в лучшем случае, расквасишь уж точно. В худшем случае сотрясение мозга обеспечено.
Ну, остаётся вопрос, как с разбегу, в эту тележку запрыгивать и нормально усаживаться (о чём уже говорил).
Цитата: Technik от 23.04.2019 21:00:27
И я Вас прощаю.
До вопросов дойдём обязательно. Хотя я вроде на вопросы, в своё время, ответил.
|
|
Luddit ( Слушатель ) |
| 23 апр 2019 в 22:30 |
Цитата: ДядяВася от 23.04.2019 21:29:19
Справедливости ради - неточно. Был свидетелем сплава по слишком большой (и быстрой) воде, неудачный контакт надувнушки с камнем приводил к тому, что парни 100+ кг рвали ремень, парни 80 кг оставались на месте.
|
|
ДядяВася ( Слушатель ) |
| 24 апр 2019 в 15:58 |
Сообщение удалено
ДядяВася
29 апр 2019 в 14:59
ДядяВася
29 апр 2019 в 14:59
Отредактировано: ДядяВася - 29 апр 2019 в 14:59
|
|
ДядяВася ( Слушатель ) |
| 24 апр 2019 в 16:03 |
Технику на https://glav.su/foru…age5255778
Аргументы железобетонные, главное чисто научные.
Долго смеялся. Вы не подумайте, что я категорически не против липучек. У самого сапоги на липучках.
PS. Пора научиться разбивать своё сообщение, а не синеньким выделять.
Аргументы железобетонные, главное чисто научные.
Долго смеялся. Вы не подумайте, что я категорически не против липучек. У самого сапоги на липучках.
PS. Пора научиться разбивать своё сообщение, а не синеньким выделять.

