IT в России и мире в реалиях мирового кризиса
1,415,901
8,485
|
|
Danila96 ( Слушатель ) |
| 20 апр 2021 19:04:27 |
Вопрос
новая дискуссия Дискуссия 653
Тут вопрос возник, но в переделе мира будет оффтоп, так что задам тут.
США потихоньку вводят разные санкции и эмбарго на it. В общем, озадачился, а зачем так мучаться, собирать разные мощные серверные установки, а потом получать за них бан, если можно поступить по другому.
Я про майнинг.
Разве нельзя выпустить какую нибудь псевдокриптовалюту, но добывать их будут путем обработки разных вычислений которые скидывает сервер. Я про аналог SETI, который был распределенной сетью в поисках внеземного разума.
Но раз так не делают, то видимо есть на то причины, так какие?
США потихоньку вводят разные санкции и эмбарго на it. В общем, озадачился, а зачем так мучаться, собирать разные мощные серверные установки, а потом получать за них бан, если можно поступить по другому.
Я про майнинг.
Разве нельзя выпустить какую нибудь псевдокриптовалюту, но добывать их будут путем обработки разных вычислений которые скидывает сервер. Я про аналог SETI, который был распределенной сетью в поисках внеземного разума.
Но раз так не делают, то видимо есть на то причины, так какие?
ОТВЕТЫ (65)
|
|
Explorer-2000 ( Слушатель ) |
| 20 апр 2021 19:53:07 |
Цитата: Danila96 от 20.04.2021 19:04:27
А как быть уверенным что результаты тех вычислений правильные

|
|
Danila96 ( Слушатель ) |
| 21 апр 2021 12:13:17 |
Не знаю, но как-то в SETI это же реализовано.
С моей точки зрения, не программиста, как минимум можно давать одну задачу разным ПК, и сравнивать результаты.
Цитата: qurvax от 21.04.2021 09:26:02
Ну типа введут санкции на поставку серверного оборудования, и нельзя будет собирать суперсервера. И мое предложение - типа костыль как можно решить проблему с нехваткой вычислительных мощностей.
|
|
AndreyK-AV ( Слушатель ) |
| 21 апр 2021 12:56:54 |
Цитата: Danila96 от 21.04.2021 12:13:17
Как показывает история, санкции даже КОКОМ, при желании можно обойти.
И опять же, суперсервера в основном из блейдов, а это ещё более широкая дорога, закупать теже блейды, у стран плюющих на американские санкции...
а далее такие компании как Т-платформа намастрячились и архитектуру и исполнение создавать и запуск делать...
|
|
adolfus ( Слушатель ) |
| 23 апр 2021 03:10:25 |
Т-платформа...
ia32/amd64 в любой упаковке – это уже остывающая вселенная. Никакие корзины с блейдами и прочие кластерные конфигурации ее не спасут – эта архитектура совершенно не масштабируется в отношении доступного процессору (ядру) объема памяти. Вы можете иметь полста тысяч узлов с сотней гигабайт памяти на каждый, но прозрачно предоставить всю эту память в распоряжение узла вы не можете. Это тупик.
|
|
AndreyK-AV ( Слушатель ) |
| 23 апр 2021 23:17:12 |
Цитата: adolfus от 23.04.2021 03:10:25
Э... не понял, а супер от сбера построенных на подобных принципах это типа новьё, как и большинство современных супер вычислительных систем.

Может все проще, на Т-платформы в 2019 был наезд с целью убить конкурента (кому?), и его пытаются с помощью ручных СМИ списать?
По сути то, люди изобрели и создали архитектуру, и могут её развивать в требуемую заказчиком сторону, т.е. что Вы понимаете под не масштабируется? ???
КМК вопрос в математике, в умении вести параллельные вычисления и распределять нагрузку.
Хотя да, я человек старой формации, и по мне лучше супермозг на супер-пупер проце, чем на сотнях супер процов, что надо учитывать и при создании приложений..., но блин если система показала качество, пусть даже она идеологически не любима, то с какой стати отнимать у неё право на жизнь?
|
|
adolfus ( Слушатель ) |
| 25 апр 2021 02:35:33 |
Современные супервычислительные системы – сегодня это микропроцессор ibm z/15. Все, что на ia32/amd64 – стагнирует, а то уже и гниет. Я не знаю, какую платформу использует сбер, но судя по остальным конторам того же цеха, это должны быть именно мэйнфреймы. С точки зрения экономической целесообразности любые движения, направленные против решний на основе ia32/amd64, идут только на пользу. Слишком уж дорогая у них и транзакция и петафлоп. В качестве универсальных вычислительных средств, они малопригодны и пришла пора все это прикрывать.
Уровень развития технологий сегодня достиг такого уровня, что вычислительная архитектура может синтезироваться под конкретную задачу и загружаться в кремний в процессе компиляции программы. Т.е. выходом компилятора является не набор инструкций процессора, а прошивка, загружаемая в ПЛИС. Она может представлять собой как конвейер,Ю так и неоднородную параллельную архитектуру. В этом случае в работе участвует практически вся поверхность кристала, а не 5-7 процентов, как это имеет место в случае универсальных процессоров.
В 2015 году интел купил альтеру для закрытых экспериментов в этой области. Пару лет назад (2017?) на НСКФ был доклад о такого рода вычислительной архитектуре, создаваемой в реальном времени для решения конкретной задачи. Ребята расказывали, что у них одна стойка на стандартных тестах производительности работает быстрее, чем кластер в четыре такие стойки.
|
|
AndreyK-AV ( Слушатель ) |
| 25 апр 2021 19:58:36 |
Цитата: adolfus от 25.04.2021 02:35:33
Узнать можно поиском

Кристофари (суперкомпьютер)
(на момент пуска в эксплуатацию 8 ноября 2019 года) 40-й в мире, седьмой в Европе и первой в России по мощности (показатели предыдущего российского лидера — системы «Ломоносов-2» — превзойдены более, чем вдвое)
ЦитатаХарактеристики отдельного узла DGX-2:
- энергопотребление пиковое — 10 кВт;
- ЦПУ — 2× Intel Xeon Platinum 8168, 2,7 ГГц, 24 ядра;
- графические ускорители — 16× Nvidia Tesla v100 32 Гбайт;
- память графических ускорителей — 512 Гбайт
- ядра CUDA — 81920
- тензорные ядра — 10240
- ОЗУ — 1,5 Тбайт
Ну и.... все те же "блейды" "вид сбоку".
.
В 1999 году народ сходил с ума от "супердом" производства HP, ЦБ РФ хавал их грузовиками как в центре, так и в регионах. Наша компания "системный интегратор" тогда проводила в доме отдыха Вороново семинар для руководства. На это мероприятие пригласили вице-президента HP по обучению. Он с самолета сразу к нам, по-русски ни бельме, но руководство НР Россия вполне нормально балакали...
Основа тренинга, продать "супердом" топу большой компании или вип-чиновнику, за три минуты, пока едешь с ним в лифте на очень высокий этаж. А главный хит выраженный словами понятными любому из нас, вызвал дружный хохот, от которого этот вельможный янки впал в ступор, чего это эти русские ржут...
Ржали мы от слова "кэш", ну да нас этот янки приехал учить давать взятки..

А к чему я это вспомнил, так нам супердома подавали как аля мейнфреймы, так и у IBM с z/15 я посмотрел описание, ну сходу трудно сказать, вроде что то не блейды, но читаю здесь и здесь и что то и не суперкомпьютер времен до блейдов и господства мейнфреймов.
Так что надо ждать взлетит или нет.
|
|
adolfus ( Слушатель ) |
| 26 апр 2021 00:30:22 |
Кристофари – обычный кластер из слабосвязанных узлов на базе x86_64 с посредственными характеристиками. Узлы не имеют доступа к памяти друг друга. Производительность ограничена производительностью интерлинков. Программировать для такого рода архитектур архисложно. Однако именно эти архитектуры агрессивно продвигаются США в лице аргонской национальной лаборатории, которая разработала mpi – библиотеку, с помощью которой программирование задач для такого рода кластеров упрощается. Однако сама лаборатория использует совершенно другие архитектуры... тадам... IBM Blue Gene.
Что касается нвидии, то деньги на ней и прочую бухгалтерию считать невозможно – у графических ускорителей вся арифметика только с плавающей запятой, даже целочисленная арифметика в полной мере не поддерживается. Это не годится для финансовых расчетов – там вычисления только с фиксированной запятой. Кстати, x86_64 тоже не имеет поддержки вычислений с фиксированной запятой, поэтому, чтобы правильно считать деньги (большие), приходится эмулировать соответсвующие инструкции через исключение недопустимой операции.Вот, кстати, IBM выдала кобол для x86_64, посмотрим, как они с этим там расправляются.
Нвидию же сбер использует для зарабатывания бабок, продавая машинное время для бигдата-процессинга и тренировки нейросетей – узлы заточены исключительно на это. Собрался рулить цифровым обществом.
|
|
dmitriк62 ( Слушатель ) |
| 26 апр 2021 13:56:06 |
Цитата: adolfus от 26.04.2021 00:30:22
Вы архитектуру Ненавидии изучали по "Техникемолодёджи" или по "Попмеханике"?

|
|
adolfus ( Слушатель ) |
| 26 апр 2021 21:24:43 |
Цитата: dmitriк62 от 26.04.2021 13:56:06
Вы, собственно, с чем не согласны? Я вот читаю самый свежайший мануал по архитектуре (менее месяца назад издан), но так и не нахожу, чем там можно деньги и прочую экономику считать. Может просветите?
|
|
mse ( Слушатель ) |
| 27 апр 2021 12:31:49 |
Цитата: adolfus от 26.04.2021 00:30:22
Сцукко, до слёз... Левая крайняя колонка, это стопка 64-битных РОН. В мире стока денех нет, чтобы обсчитать с дефолтной точностью и фиксированной запятой.
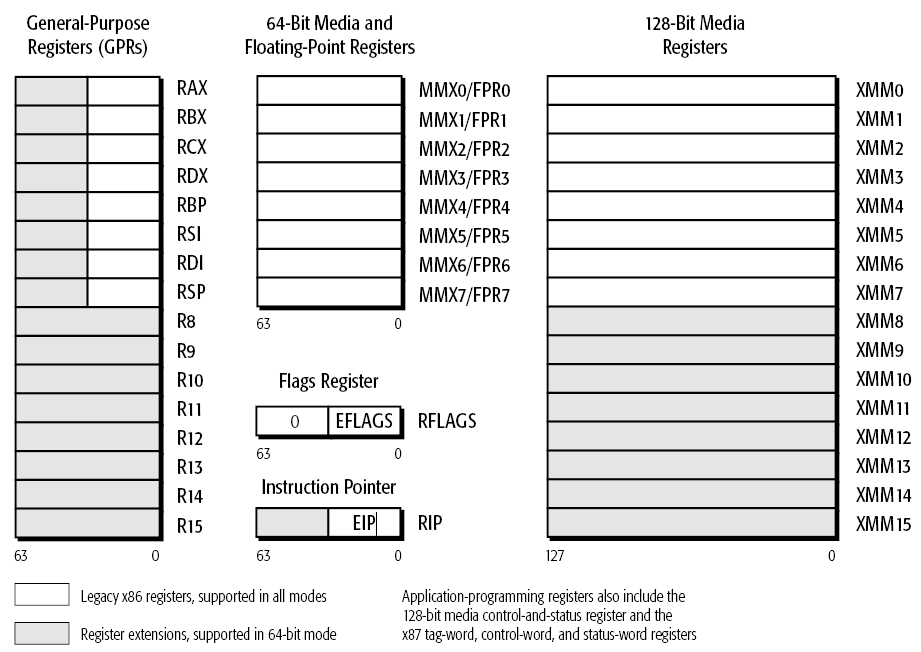
|
|
adolfus ( Слушатель ) |
| 28 апр 2021 01:10:04 |
Цитата: mse от 27.04.2021 12:31:49
... Я даже не знаю как мне на этот Ваш "до слез" отвечать... Вы программируете на ассемблере? На каком? Знаете, как используя базовую целочисленную арифметику считать сложные проценты и прочую экспоненциально-логарифмическую банковскую муйню? Достойно уважения...
Это в графике можно – "поставил" точку где-то посредине целого, типа вместо метров в миллиметрах (двоичных, разумеется), а то и в микронах работаем, и пиши в целых. С деньгами так не выйдет. Вы в лучшем случае начнете терять, либо генерировать. Опять же проблема с мультипликативными операциями – требуют коррекции, типа как для bcd. А уж как муторно возиться с дробями и рядами, используя целочисленную арифметику, не передать словами. Да и смысла нет, если есть доказанные и десятилетиями оттестированные алгоритмы, опирающиеся на доказанные примитивы и инструкции – бери и повторяй. Работая с деньгами, Вы не можете просто так сменит набор инструкций и типы данных – один и тот же банковский или экономический алргоритм при одних и тех же условиях должен выдавать одни и те же результаты вне зависимости от того, на чем он написан и на чем выполняется. Вы не задумывались, почему не переносят код с кобола, написанный полсотни лет назад и выполняющийся на мейнфреймах, на другие языки и другие платформы?
...
Деньги на x86_64 считаются, да. Но путем эмуляции реальных десятилетиями обкатанных в реальном коде инструкций, которая выполняется через исключение недопустимой операции. Компилятор (или программист) генерирует левую инструкцию, которая вне набора и вызывает исключение #UD. Пишется обработчик, который парсит инструкцию, вызвавшую #UD, и эмулирует требуемую из "кошерного" набора. Потом доказывается, что эмулянты работают так же, как и аппаратные.
|
|
Senya ( Слушатель ) |
| 28 апр 2021 07:38:43 |
Цитата: adolfus от 28.04.2021 01:10:04
Гм. Как я понял эту увлекательнейшую историю. Иррациональные величины, получающиеся при экспоненциальных расчетах всё равно невозможно выразить в виде целочисленных дробей, поэтому применяются округления (я читал что до сотой доли самой мелкой единицы - копейки, цента - но не суть). В банковском деле стандартом стали округления, автоматически получавшиеся на архитектуре 60-х годов прошлого века, и от всех новых программ требуют совпадения с теми примерами. Но сегодня копировать схемотехнические решения из седой древности. никто не будет, поэтому они эмулируются с помощью отработанных и проверенных временем алгоритмов. Не понял только, зачем это делать через прерывание, а не через вызов подпрограммы. Неужели кому-то настолько не хватает быстродействия?
ЗЫ.
И вообще просто серфясь по интернету через https миллиарды людей ежедневно проводят сотни миллиардов транзакций с длинными целыми, которые ни одна процессорная архитектура не поддерживает и ещё несколько десятилетий поддерживать не будет. И никто из этого трагедии не делает.
|
|
Longspig ( Слушатель ) |
| 28 апр 2021 10:39:19 |
Цитата: Senya от 28.04.2021 07:38:43
Вообще-то аппаратно всё должно работать начиная с 486-х процов. Флаги округления FPU выставить в нужный режим (их 4 режима. Для целочисленых вычислений вроде выбирать положено округление к нулю. Не знаю как с финансами). Ставим фиксированый множитель 10000 (для сотых долей цента) и команды FILD/FIST перекидывают число из плавающей точки в 64-битную фиксированую, в соответствие с выбраным режимом округления без лишних телодвижений. Прекрасно работал с целыми 64-битными числами без потери точности на FPU. Прерывания лишь для случая выхода за границы диапазона. Ассемблер, само-собой. На других языках элементарно может быть заложена такая же поддержка.
|
|
adolfus ( Слушатель ) |
| 28 апр 2021 12:22:12 |
Цитата: Longspig от 28.04.2021 10:39:19
С финансами это не работает. Во-первых, FPU дает относительную погрешность представления чисел (IEEE 754 обеспечивает логарифмическую равномерность чисел), а для финансов требуется абсолютная (требуется линейная равномерность). Во-второых, дробная часть двоичного числа, подлежащая округлению, всегда нечетная и в какую сторону младший установленный бит не округляй, либо недосчитаешься впоследствии, либо еще хуже – с тебя же и взыщут. Ошибка округления растет, как корень из числа операций. Правило "добавь полразряда и обрежь" работает только в школе на уроках арифметики.
|
|
Поверонов ( Слушатель ) |
| 28 апр 2021 13:45:03 |
Цитата: adolfus от 28.04.2021 12:22:12
целочисленные операции ограничиваются сложением ( со знаком ) и умножением. Как только появляется деление целочисленность заканчивается. А деление также необходимая финансовая операция для начисления процентов.
|
|
Senya ( Слушатель ) |
| 28 апр 2021 16:59:53 |
Цитата: Поверонов от 28.04.2021 13:45:03
С остатком, которое так же является целочисленной операцией.
|
|
Longspig ( Слушатель ) |
| 28 апр 2021 18:38:48 |
Цитата: adolfus от 28.04.2021 12:22:12
Пока мантисса не выходит за пределы 64-битной разрядногй сетки, равномерность будет линейной. Даже с множителем 10000 на Земле пока столько денюх нет в 64 разряда не влезть. Другое дело, что после любой операции выводящей результат за пределы целочисленой мантиссы (деления с остатком или трансцедентной) придется делать целочисленые сохранение/загрузку регистра FPU вызывающие автоматическое округление. А при целочисленом сохранении регистра FPU к этому случаю применима, например, методика "округление к четному" усредняющая накапливаемую ошибку "в обе стороны". При рассчетных задачах типа "численых методов решений диффуров" это во благо. Что требуют финансисты при округлении до 0.01 цента - я не знаю, но явно один из существующих 4-х вариантов должен попадать в их запросы.
|
|
adolfus ( Слушатель ) |
| 29 апр 2021 02:02:18 |
Цитата: Longspig от 28.04.2021 18:38:48
Нормализованное число с плавающей точкой обеспечивает только относительную точность представления, или другими словами, логарифмическую равномерность. Вблизи нуля числа расположены чаще, вдали – реже.
|
|
Longspig ( Слушатель ) |
| 29 апр 2021 21:27:41 |
Цитата: adolfus от 29.04.2021 02:02:18
"Относительной" точность в FPU становится лишь выше значения 2**64-1 (знак забирает разряд из поля порядка и тут не участвует). Но операции целочисленого сохранения всегда знаковые, так что разряд теряем (2**63-1). До этого предела, точность представления любого целого числа в FPU абсолютная.
Прекрасно работал с целыми 64-битными числами через FPU.
|
|
adolfus ( Слушатель ) |
| 02 май 2021 05:04:24 |
Цитата: Longspig от 29.04.2021 21:27:41
Вы просто не понимаете, что такое "абсолютная точность" и что такое "относительная точность", а также что такое "логарифмическая равномерность".
Вещественное число за редчайшим исключением (как говорят математики, "везде, за исключением выколотых точек") не может быть представлено в формате IEEE 754 точно. Это называется "погрешность представления".
У любого вещественного числа есть два ближайших к нему числа, которые точно представимы в формате IEEE 754 – одно меньше, другое больше.
Это имеет место для представления вещественных чисел по любому основанию в форме мантиссы и порядка.
Разность между этими двумя рядом расположенными числами тем меньше, чем ближе к нулю они расположены. Зато их отношение остается постоянным для всего диапазона. Это называется "логарифмическая равномерность представления вещественных чисел в форме с мантиссой и порядком".
Для целых, в отличие от вещественных, какие вы бы не брали рядом расположенные числа, у них разность будет постоянна, а отношение тем ближе к единице, чем числа больше. Это же справедливо и для формата с фиксированной запятой, поскольку она есть не что иное, как масштабированное целое.
Если сходу не понятно, то просто возьмите два любых числа в формате IEEE 754 и помасштабируйте, меняя порядок. Разность между ними будет различной, а отношение останется без изменения. Это и называется относительной точностью. По аналогии с погрешностью измерений. Только здесь погрешность представления.
...
Окуда вы взяли "2**64-1", не понятно. Это число никакого отношения к FPU не имеет вообще. Вот из IEEE 754-2008 таблица с параметрами
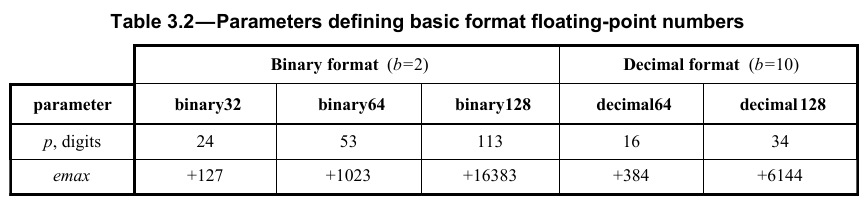
И еще – FPU не работает с целыми. Просто почитайте "Intel 64 and IA-32 Architectures Software Developer's Manual" – там все расписано. Может загружать целое, при этом оно преобразуется во внутренний формат и все операции выполняются как с плавающими. Это значит, что при арифметических операциях Вы получите результат, отличный от того, что получили бы на CPU. Будете делить 5 на 2 и получите либо 2, либо 3, в зависимости от того, как будет установлено округление в RC. Вот цитата:
"The x87 FPU recognizes and operates on the following seven data types: single-precision floating point, double-precision floating point, double extended-precision floating point, signed word integer, signed doubleword integer, signed quadword integer, and packed BCD decimal integers.
With the exception of the 80-bit double extended-precision floating-point format, all of these data types exist in memory only. When they are loaded into x87 FPU data registers, they are converted into double extended-precision floating-point format and operated on in that format.
У меня складывается впечатление, что Вы вообще никогда с плавающей запятой не работали. Разве что в питоне или матпакете.
|
|
adolfus ( Слушатель ) |
| 28 апр 2021 12:03:59 |
Цитата: Senya от 28.04.2021 07:38:43
Транзакции не люди проводят, а программы, которые работают не у миллиардов людей, а на конкретных серверах, и этим серверам все эти длинные целые, что у людей, которые эти самые транзакции инициируют, до фиолетовой лампочки. Там свои типы данных, свои операции, алгоритмы и прочее. И никто не собирается в ближайше время это все менять и переделывать. Перманентно возникающие передельщики этой "седой древности" уже более, чем полвека пытаются переплыть на "модную, молодежную современность", натыкаются на проблемы, в том числе и округления, которые почему-то никак не получается нормально решить и сдаются. Если в 80-х и 90-х за эту деятельность хоть как-то платили (таки я даже за это получал), то сегодня предпочитают вкладывать деньги в развитие этой самой "седой древности" и обучение общению с ней. Мало того, "мягкую" компоненту этой "седой древности" даже в граните отлили. Мало кто в такой гранит может. Не только лишь все
 И что-то я не вижу
И что-то я не вижу Помимо транзакций есть еще куча алгоритмов, в том числе и те, результатом которых является "округление иррациональных результатов" . Кстати, как вы будете округлять? Например, ссуду денег в рост? Умножаете длинное целое денег на процент и ... получаете дробный результат – деньги плюс "хвост". B так каждый день. В результате у вас накапливается дробная часть. Допустим, перед умножением было масштабирование на 8 разрядов и после умножения нужно все отмасштабировать на 8 разрядов назад, а у вас в этих самых разрядах не нуль. И как мы с ними поступим? И что получим в приросте в конце года?
|
|
Senya ( Слушатель ) |
| 28 апр 2021 16:59:11 |
Цитата: adolfus от 28.04.2021 12:03:59
Речь о том, что отсутствие в какой либо архитектуре аппаратной поддержки некоего узкого класса операций никак не ограничивает её применение и не является ни неоспоримым достоинством, ни фатальным недостатком.
Цитата: adolfus от 28.04.2021 12:03:59
Не, далеко куцему до зайца, в смысле до BCD формата. Который уже полвека как абсолютно бесполезен, но пихается куда только можно.
|
|
GrinF ( Слушатель ) |
| 28 апр 2021 21:58:53 |
Цитата: adolfus от 28.04.2021 12:03:59
еще раз ... для транзакций вообще не нуэжны даже опеаторы умножения и деления ... там все ограничивается плюсами и мнусами и то есть за глаза хватает INT64... для расчета процентов конечно ужо нужны опепации деления и умнодения, а потом отурываем инструкции минфина или цб о расчетах и смотрим чего там в какую сторону округляется... прирчем это операция опять таки будет управляющая, ибо расчетная это списание/начисление со/на счета с точностью до копеек.
|
|
mse ( Слушатель ) |
| 28 апр 2021 19:50:10 |
Цитата: adolfus от 28.04.2021 01:10:04
"Цуко, до слёз"-2...Целочисленная арифметика и экспоненцыально-логарифмическая банковская муйня. Эта пять, ящетайу...
Да, я пишу на ассемблерах, в том числе. На х86, правда, давненько не приходилось. А што? И , ессно, с целочисленки перейти в плывучку и назад, тоже, каг два пальца об асфальт. Этому даже в средней вышшей школе учат.
Цитата: adolfus от 28.04.2021 01:10:04
Потому, что это чертовски дорого ,переписывать гектары рабочего, многократно проверенного кода на какой-нить Фортран или Пасквиль. Да и смысла нет. Кобол стабильно в десятке самых актуальных языков.
Мейнфреймы, кстате, имели примерно такие-же системы команд, что и х86. Никаких волшебных тёплых
Цитата: adolfus от 28.04.2021 01:10:04
Чо вы несёте? Вызвать эксепшынс, чтобы на коленке, за углом, чотатам накодить? А сразу накодить вместо эксэпшына Маммон не позволяет?
Ух, дичь какая! Аж спать перехотелось, пойду кофию накачу, вдруг полегчает.
|
|
adolfus ( Слушатель ) |
| 29 апр 2021 02:57:27 |
Цитата: mse от 28.04.2021 19:50:10
Откуда Вы эти глупости черпаете? Какая система команд? Совершенно различная архитектура. Там даже стека не было. Совершенно различное кодирование символов. Совершенно различные системы команд. Если что и совпадало, так только директива using. Правда для x86 это подсказка ассемблеру по сегментному регистру, а для мейнфрейма по базовому. И на том и на другом работал. Совершенно разные isa и методы программирования.
|
|
mse ( Слушатель ) |
| 30 апр 2021 00:53:54 |
Цитата: adolfus от 29.04.2021 02:57:27
Чо вы несёте? Система команд, это логические и арифметические операццыи над данными в регистрах и памяти. Вся это сегментная и косвенно-регистрово-индексная адресаццыи, это только обмазка вокруг арифметики и логики. А тонкости архитектуры способен оценить только системщик. Прикладнику дали компилятор и насрать ему, на чом он работает, на ИБМ360 или на каком х86.
|
|
DarkRaider ( Слушатель ) |
| 30 апр 2021 11:47:56 |
Цитата: mse от 30.04.2021 00:53:54
Уважаемый mse, несмотря на то, что я не согласен с автором текущего срача, уважаемым adolfus'ом, но ему простительно, он человек сугубо увлекающий в своей категоричности всегда, всё таки надо стараться быть объективными. Прикладному программисту действительно всё равно как компилятор или интерпретатор транслирует его программу в машинный исполняемый код и под какую архитектуру. Чаще всего трудности вызывают только различные неудобства и ограничения вызванные целевой платформой, но есть разные парадигмы программирования, типа постфиксной нотации языка Форт, которые могут быть привязаны и к архитектуре (раньше его очень любили пихать во встраиваемое ввиду небольшого размера интерпретатора) и они реально совсем "другие".
В остальном, "прекрасные маркизы", по моему пора просто признать правоту adolfus'a как давнего популяризатора Кобола и остаться при своём мнении, что на современных архитектурах можно делать всё тоже самое, что и на древних, но жадные банкиры ещё не дозрели начать платить денег, за разработку "с нуля", потому что "перевести" старые алгоритмы "по очереди" - практически не решаемая задача. А писать с нуля всю цепочку - страшноватенько.
|
|
mse ( Слушатель ) |
| 30 апр 2021 13:04:51 |
Да банкиры правы: зачем списывать в утиль программы, которые уже лет 50 вылизывали? И программ этих не 10-20, а тыщщи и десятки тыщ. И размеры у них конские. И поддержка уже, наверняка, не вполне соображает, что там в глубине глубин. К тому-же кто-кто, а Кобол в защите не нуждается. Он стабильно в десятке наиболее актуальных языков.
"Солнце всходит? Заходит? Не трогай, сломаешь."
|
|
dmitriк62 ( Слушатель ) |
| 30 апр 2021 13:58:10 |
Цитата: mse от 30.04.2021 13:04:51
Абсолютно согласен.
Вот только даже зная что-то о Коболе (редкостная окаменелость!), делать выводы о современных архитектурах — это кружковский зашквар...

|
|
Senya ( Слушатель ) |
| 30 апр 2021 15:19:05 |
Цитата: mse от 30.04.2021 13:04:51
Тем более подо что переписывать? х86/amd64 на сегодня такая же виртуалка, крутящаяся над реальными архитектурами процессоров, за которыми я так уже давно соскучился следить. Кто знает, сколько там физических регистров общего назначения? Последняя информация, которая мне попадалась, больше сотни, прозрачно для программиста подменяющих друг друга.
|
|
DarkRaider ( Слушатель ) |
| 01 май 2021 18:17:59 |
Цитата: mse от 30.04.2021 13:04:51
Смею заверить (№1), из личного опыта - получив 5 лет назад в эксплуатацию и разработку одну из информационных систем города, отсутствие полных исходников - было исключительно нашей половой трудностью. Смею заверить (№2) - уже через 3 года департамент считал эту систему "нашей" (со всей долей ответственности). В действительности, пришлось часть чёрных ящиков переписать с нуля, а вторая часть благополучно дожила до естественной смерти (вывода интеграции со смежной ИС из эксплуатации) и уже целенаправленно была заменена новыми механизмами. При этом большинство информационных систем, даже очень проблемных - сложно вывести из эксплуатации целиком их стараются дорабатывать и модифицировать в большинстве случаев.
Мы обсуждаем банковское ПО, кластеры под него и кобол. Как мы уже выяснили, другие языки не заточены на решение этих задач так как кобол - отсюда и необходимость эмуляции на функциональном уровне, даже без учёта физической архитектуры.
|
|
GrinF ( Слушатель ) |
| 28 апр 2021 21:50:23 |
Цитата: adolfus от 28.04.2021 01:10:04
Вы камерад мешаете в кучу - расчетные программы - там где деньги деньги со счета - на счеит гоняют... и управленческие программы - всякие там опционы , кривые доходности, прогнозирование потока платежей, VaR и прочий риск -менеджмент. Для первого достаточного INT64 с переводом все в копейки даже для уровня казаначейства Минфина... Для вторых нужны действительно плавающие числа и даже возможно спецалзированное железо.Но количество пользователей на порядок а то и на 2 меньше у второго класса программ...Так шо считать деньги можно считать и спомощью целочсленной арифметики...
Цитата
Это в графике можно – "поставил" точку где-то посредине целого, типа вместо метров в миллиметрах (двоичных, разумеется), а то и в микронах работаем, и пиши в целых. С деньгами так не выйдет. Вы в лучшем случае начнете терять, либо генерировать. Опять же проблема с мультипликативными операциями – требуют коррекции, типа как для bcd. А уж как муторно возиться с дробями и рядами, используя целочисленную арифметику, не передать словами.
Ну не знаю- не знаю... Есть у меня родственник ... как-то 3 года назад увлекся роботами ну и начал сам мало-помалу писать проги... в последнее время дорщел до программирования FPGA... Ну звонит месяца три назад и спрашивает а не зная ли я алгоритма деления который бы не использовал плавающие числа - ему нужно скорость движения быстро оценить по показаниям датчика скорсти вращения, ибо FPGA куда быстрее работает с целыми числами нежели с плавающими. Я ему предложил разлодение в ряд тейлора прменить, а потом вспомнил что есть более быстрые алгоритмы деления в вике
Цитата
Да и смысла нет, если есть доказанные и десятилетиями оттестированные алгоритмы, опирающиеся на доказанные примитивы и инструкции – бери и повторяй. Работая с деньгами, Вы не можете просто так сменит набор инструкций и типы данных – один и тот же банковский или экономический алргоритм при одних и тех же условиях должен выдавать одни и те же результаты вне зависимости от того, на чем он написан и на чем выполняется. Вы не задумывались, почему не переносят код с кобола, написанный полсотни лет назад и выполняющийся на мейнфреймах, на другие языки и другие платформы?
Обыкновенная жаба... Людей давит жаба нанят новую комманду и переписать алгоритмы...Потом начинается а\песня когда оказывается аппаратный сбой, а заменить нечем ибо такой хлам уже не выпускают ...Это полбеды - можно нанять электронщиков - задорого но сделают... проблема возникает дальше - когда начинают умирать разработчики...Я уде лично такие грабли наблюдал... тогда как не подрыгивай с бубеном - все пипец приплыли - выкладывай деньги на програмеров
Цитата
...
Деньги на x86_64 считаются, да. Но путем эмуляции реальных десятилетиями обкатанных в реальном коде инструкций, которая выполняется через исключение недопустимой операции. Компилятор (или программист) генерирует левую инструкцию, которая вне набора и вызывает исключение #UD. Пишется обработчик, который парсит инструкцию, вызвавшую #UD, и эмулирует требуемую из "кошерного" набора. Потом доказывается, что эмулянты работают так же, как и аппаратные.
|
|
adolfus ( Слушатель ) |
| 29 апр 2021 03:13:20 |
Цитата: GrinF от 28.04.2021 21:50:23
Для реализации на ПЛИС (Virtex 5 и 7) есть итерационный алгоритм деления на онове метода Ньютона-Рафсона. Вроде в библиотеке, что зайлинх продает, этим методом делят. Вместо итераций используется конвейер из нескольких арифметических блоков.
|
|
AndreyK-AV ( Слушатель ) |
| 28 апр 2021 11:01:51 |
Цитата: adolfus от 26.04.2021 00:30:22
Нда.... попробую по тому что понятно.
1. Сбер давно стремится стать IT компанией с банковской лицензией, впрочем почти стал давно, и основной софт ему разрабатывают «Сбербанк-технологии". Кристофари это для них и понты, и давление на конкурентов, и да это обычный кластер, только один из мощнейших в мире....
2. Насколько я знаю, в региональных центрах у них вполне себе работают ЦОД-ы на x86_64,
3. По поводу так зацепившего вас Nvidia, вот тут как мне кажется поворот интересный и в иную сторону. Делали они этот Кристофари в сколковском муравейнике, притом в момент бешенного интереса к майнингу и криптовалютам, вот есть у меня подозрение, что собирались если не наберётся постоянных заказчиков то майнинг.
3.1. Есть и ешё момент, Их образовательный проект, для которого как мне кажется представленная архитектура удобнее чем один супермозг, по сути же в рамках единой системы нужно держать о обрабатывать массу цифровых двойников образовательных учреждений, притом каждого со своей непересекающейся ни с кем информацией.
4. И наконец. То что для банков ИТ это основное производство, стало понятно ещё в прошлом веке, но вот превращение банков в ИТ компании в рамках рыночной экономики или госкапитализма который опять же предполагаеи рынок в плане финансовых услуг, это пмсм откровенно нечестная конкуренция, так как крупнейшие банки знают всю подноготную клиентов, их финансовые отношения между собой, и хоть все якобы конфидициально, но блин о какой конфидициальности можно говорить в рамках идеологии "только бизнес и ничего личного" , обвязаной голубой лентой так называемой экосистемы. Плюс прямое посягательство на функции государства и регулируемые государством, как то образование&воспитание&медицина... вне досягаемости регулятора.
|
|
Поверонов ( Слушатель ) |
| 24 апр 2021 16:10:48 |
Цитата: adolfus от 23.04.2021 03:10:25
Есть масштабируемые базы данных в памяти - при необходимости узлы могут быть связаны выделенными сетевыми интерфейсами на световолоконных кабелях. Базы данных могут шардировать данные так что все доступны из каждого узла но каждый узел хранит лишь свою часть общей базы.
|
|
adolfus ( Слушатель ) |
| 25 апр 2021 02:01:52 |
Цитата: Поверонов от 24.04.2021 16:10:48
Выделенные сетевые интерфейсы не обеспечивают однородного доступа к оперативной памяти требуемого объема. В этом отношении MPP-решения на основе SMP/UMA более удобны и производительны. Вместо mpi и прочих send/receive используются обычные операторы присваивания. Кроме того, системы с однородной памятью компактнее, дешевле, надежнее, меньше жрут электричества и лучше охлаждаются. Четыре узла по 16 ядер и 256 Гбайт каждый с полносвязным интерконнектом стоят больше, чем один SMP/UMA c 64 ядрами и терабайтом памяти. При этом производительность первой платформы будет определяться пропускной способностью интерконнекта, а второй – памяти. Это, как минимум, раз в сто и больше.
Распределенные цивильные системы появились не от того, что они такие класные и удобные, а потому, что в те времена, когда они появились, wintel зачищали поляну под свою убогую говноплатформу и вырубили все ростки нового и перспективного везде, куда только смогли дотянуться. Кто спрятался тогда в подвалах, как IBM, тот только и остался. В результате всего этого и появились "шланговые" кластерные архитектуры на низколатентных сетевых интерфейсах для счета больших моделей, которые не могли разместиться в 64-х PAE-гигабайтах платформы винтел. Все распределенные архитектуры – дети технологической убогости.
Что касается баз данных, то распределенные СУБД появились тоже не вследствие какого-то прогресса в методах хранения и доступа к данным, а из-за перманентно нерешаемых проблем с масштабированием аппаратной платформы wintel, на которую посадили даже oracle. Распределенные архитектуры появились именно из-за необходимости хоть как-то решить эту проблему. Однако, при таком "распределенном масштабировании" пришлось выбирать между производительностью и ACID. В результате в жертву принесли ACID, в связи с чем пришлось отказаться и от SQL. Но придумали для этого специальные кейсы использования, название, и стали гордиться. А к тому времени, когда стало возможным сочетать и производительность и ACID, уже не осталось бабла, которое можно на этом качать – все вокруг занято распределенными non-ACID решениями, которые усиленно оберегаются от посягательств.
|
|
qurvax ( Слушатель ) |
| 21 апр 2021 13:22:39 |
Цитата: Danila96 от 21.04.2021 12:13:17
Я помню лет уже 5-6 тому хранилища закупал, нетаппы там, эквалоджики всякие, на компелент облизывался да. Ну так вот, там уже тогда было соглашение со списком стран, куда хрена лысого а не хранилища. И РФ там была в полный рост. А серверное оборудование, мне так чуется, на процентов, наверное, 70 существующего в эксплуатации вот прям на щас, обеспечивает не математические рассчеты да моделирование всякое там, а запуск и поддержание чухни навроде VDI и бухгалтерий с базами. Причем тупейшими, с т.з. эффективности, методами - наворочена куча из контейнеризации, виртуализации и костылизации, а поверх всего сего модно-молодежного - вм с вындаус2к и 1С
 Кговавый энтерпрайз такой кговавый.
Кговавый энтерпрайз такой кговавый.
|
|
qurvax ( Слушатель ) |
| 21 апр 2021 09:26:02 |
Цитата: Danila96 от 20.04.2021 19:04:27
Осмысленные вычисления и "блок" крипты различаются, в том числе, и предсказуемостью "стоимости" рассчетов. Не, ну наваять, наверное, некую систему, нарезающую чейто похожее на равные "единицы", наверное можно - но зачем (читать "где бизнесс?")?
|
|
Podli ( Слушатель ) |
| 22 апр 2021 09:21:34 |
Цитата: Danila96 от 20.04.2021 19:04:27
Очень и очень немного реальных задач получится решить таким способом. Просто потому что очень немного задач позволяют распараллелить вычисления на множество слабых машин с минимумом обмена информации между ними.