Были или нет американцы на Луне?

Цитата: Pаssаt от 05.02.2020 09:10:23Между прочим, и в работе Кокурина, и в работе по аполлону 11 явно указано количество регистрируемых фотонов на импульс. Вы этого не заметили? Вы статьи читали? Или только на картинки глядели?

Цитата: Technik от 06.02.2020 10:21:32Дык с самого начала было сказано - ДРУГОЙ снимок. Но тема та же мааааленькие   лунные камешки.

Цитата: photo_vlad от 06.02.2020 11:29:15Ага, аргументация учёного мужа на основе понятия "вера".
Самая что ни на есть научная, вы просто ничего в этой науке не понимаете, бгг!

Цитата: ДядяВася от 04.02.2020 18:37:23Там на ковре самолёте летали. Я ж не буду утверждаю, что проще сделать ковёр самолёт, чем снять такой эпизод.

ЦитатаПосле выхода фильма ко мне обратился американский режиссер с предложением делать спецэффекты для его картины, – поведал Данелия. – Сказал, что его впечатлило, как у нас летает пепелац.
А я ему: «А там нету спецэффектов. Военные дали нам гравицапу. Мы поставили ее на декорацию, и она летала. Вы обратитесь к русским военным. Это их разработки. А то вдруг я вам тайну расскажу. У нас с этим строго, меня будут считать шпионом».
Он и обратился...
https://newdaynews.ru/culture/541597.html

Цитата: Liss от 05.02.2020 11:32:34Ничего Вы не объяснили. Не знаете Вы, какими манипуляциями получены числа 27 и 21, не понимаете, почему ширина сигнала измеряется в микросекундах и что вообще является для автора сигналом, но при этом фантазируете, что они означают, и пытаетесь перенести на другие работы. Это – подлог.

Цитата: sharp89 от 06.02.2020 00:16:47Презумпцию определяют не сетевые анонимы исходя из своих фантазий и хотелок. В обсуждаемом вопросе презумпция заключается в том, что позиция мирового научного сообщества является верной. Почему именно она - да потому, что позиция мирового научного сообщества является верной по подавляющему большинству вопросов, по которым она выдвигает какие-либо утверждения.

Цитата: sharp89 от 06.02.2020 00:16:47

Цитата: viewer от 05.02.2020 23:25:47А скажи-ка мне дружок, что такое Манжерок какого цвета лунная поверхность?
Только без многословных соплей, а кратко - такого-то . 

Разная в зависимости от местности и от падающего освещения. Почитайте астронавтов на этот счет, они вам расскажут.

Цитата: sharp89 от 06.02.2020 00:16:47Ну я так и думал, что по теме изотопного датирования лунных образцов вы ничего членораздельного выдавить не сможете.

Цитата: ДальнийВ от 06.02.2020 12:00:03П.С.
Как видим никто из учёных не сомневается в этих числах и в свойствах УО.

Цитата: Pаssаt от 05.02.2020 13:34:07Вы уже вконец обнаглели. Это вы, а не я не в состоянии обосновать свое собственное утверждение, но почему то этого от меня требуете.

Было бы здорово, если бы вы еще свой вопрос понимали бы.
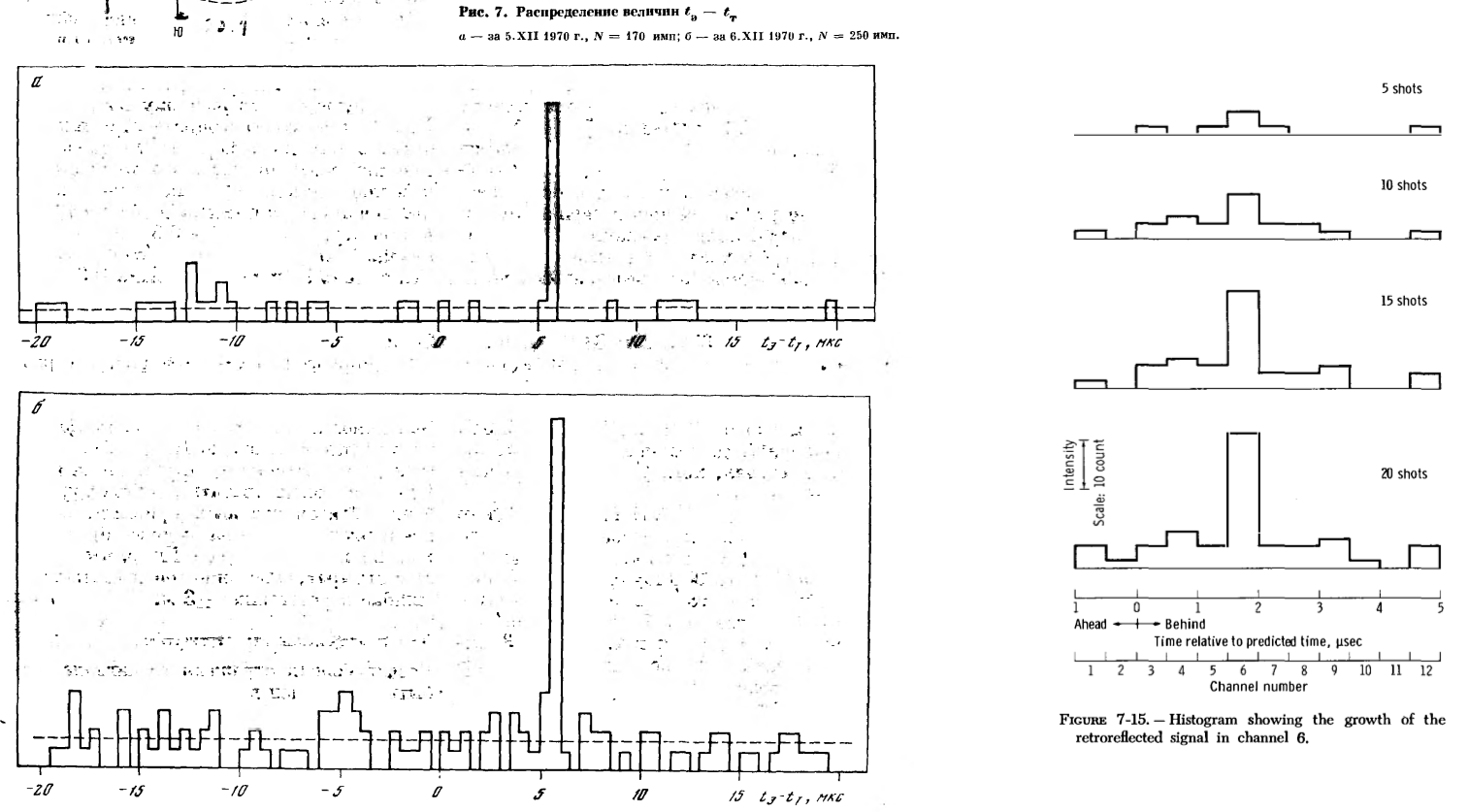
А по поводу сравнения эффективности, попробуйте проанализировать два аналогичных графика. Один вам знаком, а другой - это А11.
Что скажете насчет эффективности? Не забудьте внимательно подписи к графикам почитать.


Продолжайте и дальше объемы своих безграничных знаний демонстрировать.

Цитата: viewer от 06.02.2020 12:10:29логика лженаука это уже аксиома.

ЦитатаРазная цвета?

ЦитатаТак почитал! Она (цвета ) у них даже одной и той же местности и при одном и том же падающем освещении - разная!

ЦитатаЭто тоже будет являться доказательством, что человек (уже советский) топтал лунную поверхность?

Цитата: sharp89 от 06.02.2020 11:15:15Гравитация, сэр.

Цитата: Протеин от 06.02.2020 11:08:552. Читайте посты выше, камерады уже растолковывали графики Кокурина.
С уважением

Цитата: ДальнийВ от 06.02.2020 11:21:02Кстати, то что Фоллер жульничал(возможно невольно) легко выявляется по среднему уровню солнечного шума.
Он у него "плывёт", а должен быть константой.

Цитата: sharp89 от 05.02.2020 13:58:08Про "единицу освещаемой площади" опроверги как раз и забывают, думая почему-то, что отражатель должен вернуть в 10-100 раз больше, чем весь грунт, на который попадет пятно лазера.

Цитата: bvlad от 05.02.2020 14:07:08Американский астронавт Эдвин Олдрин рассказал о своих наблюдениях во время миссии "Аполлон-11" Американский астронавт Эдвин Олдрин рассказал о своих наблюдениях во время миссии "Аполлон-11". Он утверждает, что видел на Луне признаки существования инопланетных существ, но эта информация длительное время скрывалась от общественности. Эдвин Олдрин сообщает, что сразу же после возвращения на поверхность Земли он обнародовал данные о полете, а также о наблюдаемом НЛО, но его слова не приняли всерьез. Астронавт даже прошел детектор лжи, который не показал отклонений во время теста. Немного позже американский исследователь поделился своей историей с общественностью и охарактеризовал инопланетное существо, с которым столкнулся на Луне. Олдрин уверял, что, находясь на поверхности спутника Земли он неоднократно наблюдал яркие вспышки света. К слову, ни на одном из снимков, привезенных из экспедиции, необычных явлений запечатлено не было. По словам астронавта, NASA приложило все усилия, чтобы своевременно удалить важные доказательства. Напомним, что недавно в Сети была распространена информация о появлении инопланетных технологий на Луне. Объект был расположен в одном из кратеров и не был похож на камень или обломок.

Источник: https://dni24.com/exclusive/256823-amerikanskij-astronavt-jedvin-oldrin-rasskazal-ob-jekspedicii-apollon-11.html?utm_referrer=https%3A%2F%2Fzen.yandex.com&utm_campaign=dbr

Цитата: Просто_русский от 06.02.2020 11:22:25Обратите внимание, что означает Аг.

Цитата: Просто_русский от 06.02.2020 11:22:25Если у Земли значение альбедо зависит (очень сильно) от облачности, то как Вы умудрились (именно Вы, а не авторы книги, они до такого не додумались) измерить альбедо Луны в новолуние? Веселуха с вами прям.

Цитата: ДальнийВ от 06.02.2020 11:31:10А ну ка скорее покажите нам данные и расскажите как Кокурин и Фоллер узнавали сколько фотонов от УО приходило в ФЭУ за один импульс.
П.С.
А вот выявился и скромный "отличник" Старого.
Получите его медальку "Ни ухом ни рылом!"

Цитата: ДальнийВ от 06.02.2020 12:00:03Как видим никто из учёных не сомневается в этих числах и в свойствах УО.

Цитата: ДальнийВ от 06.02.2020 12:40:28Даже и не знаю, ну как можно верить больным и неадекватным американским астронавтам об  их якобы полётах на Луну?

Цитата: Luddit от 06.02.2020 12:24:57Так просто гравитации недостаточно. Чем меньше космическое тело, тем крупнее на нём рельеф (вплоть до известного примера с кометой в виде гантельки). На луне этот крутой рельеф сильно сглажен метеоритными бомбардировками, но тем не менее угол естественного откоса довольно большой (смотрим на крутизну бортов колеи советских и китайских луноходов). 
С холма крутизны как аполлоновских фото такая глыба и на Земле не поедет.

Цитата: Протеин от 05.02.2020 15:51:33Тут Вы не правы.
Давайте рассмотрим поближе.
Есть горизонтальная поверхность 1 м кв.  На нее попадает 100 фотонов.
В случае с грунтом отразиться назад 7 фотонов, именно назад (если поверхности отражения параллельны).
В случае с УО отразиться 100 фотонов.
Пятно в 2.5 км.кв равно  4908738 кв.м х 7  отразит = 34 361 166  фотонов.
Из этой массы отраженных от пятна лазера, нужно отфильтровать всего 100.
При этом скорость отражения  одинакова как от УО так и от поверхности.  + камни и другие твердые поверхности, их альбедо выше.
С уважением