Были или нет американцы на Луне?

Цитата: Сагитариус от 04.11.2023 22:28:07Это ваша версия. У ученых такой версии в статье нет..
Гуглоперевод той статьи.

- "Возможно, необычные условия смогли возникнуть на Луне очень локально и на короткий промежуток времени, а образец является результатом этого отклонения от нормы, - продолжает Немчин. - Однако более простое объяснение заключается в том, что образец 14321 сформировался на Земле и попал на Луну в составе метеорита, получившегося около четырех миллиардов лет назад при столкновении астероида с Землей. Оно сопровождалось выбросом земного вещества в космос и на спутник нашей планеты."

Либо "фантастический блокбастер" либо фейковый "лунный грунт". Какой вариант вам больше нравится? 

Цитата: RusBelS от 04.11.2023 22:53:53- "Возможно, необычные условия смогли возникнуть на Луне очень локально и на короткий промежуток времени, а образец является результатом этого отклонения от нормы, - продолжает Немчин. - Однако более простое объяснение заключается в том, что образец 14321 сформировался на Земле и попал на Луну в составе метеорита, получившегося около четырех миллиардов лет назад при столкновении астероида с Землей. Оно сопровождалось выбросом земного вещества в космос и на спутник нашей планеты."

Либо "фантастический блокбастер" либо фейковый "лунный грунт". Какой вариант вам больше нравится? 

Мне нравится не считать себя экспертом по всем вопросам.
Ученые разберутся и без нашей помощи, надеюсь.

Цитата: Сагитариус от 04.11.2023 20:34:10Это неправда.
Коновалов взял схему из Википедии. А размеров там нет.

Не соглашусь. Это не схема. На чертежах общего расположения размеры проставлять не обязательно. Но масштаб соблюдается. Конечно, при оцифровке возможны некоторые искажения, да и монитор, в зависимости от выбранного разрешения вносит свои, но это мелочи.
Дело в другом. Коновалов прекрасно знал размер площадки перед входом:
Как он из 107 см выдавил 91 см - не объясняет. При том, что справедливо считает, что люк должен открываться полностью. А он - 42 дюйма или 106 см.
Главная же уловка - в фигуре астронавта. Я уже говорил, что при наличии хоть какой-то силы тяжести, строго горизонтально входить невозможно.
Но и фигуру Коновалов масштабировал до ранее принятого им вывода, что ростом она должна быть двухметровой. Соответственно и толщина отмасштабирована. Подписанные 185 см - фейк, всё легко проверяется.

Цитата: Vist от 04.11.2023 23:16:30Не соглашусь. Это не схема. На чертежах общего расположения размеры проставлять не обязательно. Но масштаб соблюдается.

Хотя бы масштаб был бы указан. На картах наносится и масштаб и линейка для этого.

Цитата: Vist от 04.11.2023 23:16:30Дело в другом. Коновалов прекрасно знал размер площадки перед входом

Вы делаете комплимент его знаниям. 
Впрочем, ему могли и показать.

Цитата: Vist от 04.11.2023 23:16:30Подписанные 185 см - фейк, всё легко проверяется.

Конечно, фейк. 
Расчет на простачка, оболванить обывателя.
Который не поинтересуется реальными размерами кабины.
Но отложится, якобы и в лунный модуль-то никак не влезть.

Цитата: Сагитариус от 04.11.2023 22:42:28Как же глупо отрицать, что когда измеряете по тени, нужно учитывать положение солнца.

Камрад, как математик - математику: если бы ракета летела строго на солнце, то Вы были бы абсолютно правы. Но "в сторону солнца" даже с небольшим углом, если этот угол склонения ракеты и форма подстилающей тень поверхности не изменились значительно за рассматриваемые 1,37сек дает нам условие для выполнения требований одной теоремки:

"Параллельные прямые (лучи солнца - оно далеко, можно принять, что лучи "почти параллельны") на пересекающихся прямых (участки прямых траекторий ракеты и тени) отсекают пропорциональные отрезки."

Т.е. если тень прошла 1,6 своей "не важно какой" длины (например, по точке кормы), то и ракета прошла 1,6 своей "известной заранее" длины: 1,6*110,8 = 160 (почему не 177?). И угол ракеты к солнцу - важно, чтобы он был хоть как-то отличен от нуля и не сильно менялся в рассматриваемом интервале времени. На приведенном в сообщении слайде видно, что "на глазок" длина тени не сильно изменилась, т.е. можно предположить, что склонение ракеты к плоскости облака не изменилось.

Но для попадания в условие теоремы все-таки нужно "одно хорошее условие": участки прямых. Сильно сомневаюсь, что подстилающая тень поверхность - плоскость, чтобы траектория тени дала отрезок прямой. Сильно сомневаюсь, что склонение ракеты не менялось - она же в плоскость экватора, если не ошибаюсь, должна выйти. И на "глазок" такие задачи решать не хорошо.

Но если длина тени на этом участке постоянна, то это условие того, что траектории и ракеты, и тени именно на этом кусочке можно принять за "условную прямую", а участок  подстилающей поверхности - за "условную плоскость", и Ваши оппоненты, скорее всего, правы: так делать можно. Причем, взаимное расположение облака (тени), ракеты и солнца не важно: пусть они хоть в 5D взаимно расположены - все прекрасно проецируется на плоскость, заданную тремя точками: солнце, нос и корма ракеты (лишь бы они не лежали на одной прямой = "ненулевой угол на солнце"), - а в ней указанная теорема верна.

Правда, в ответе мы получим скорость ракеты относительно наблюдателя. Тут собака и порылась: ракета летит над землей , наблюдатель "едет" на земле вместе с ее поверхностью, немного опережая/отставая от ракеты. Тогда для полноты картины надо посмотреть на скорость наблюдателя на этой параллели. И прибавить/вычесть ее из рассчитанной скорости ракеты. Ну и скорость земли относительно солнца надо куда-то прилепить: все-таки 30 км/с - это не "хухры-мухры". И тут же скомпенсировать силой тяжести на ракету - ракета-то еще даже первую космическую не набрала и тем более не покинула гравитационный колодец. Так что Земля ее "за собой" вокруг Солнца еще довольно бодро тянет. В общем, задачка определения собственной (приборной?) скорости ракеты получается несколько сложнее, чем "160/1,37".

С уважением.
P.S.: Ну и, опять же, скорость ракеты в данном случае - это 3D-вектор. То, что проекция ее модуля (длины) на систему отсчета, связанную с наблюдателем, равна 115±12 м/c в данном конкретном случае ничего не говорит нам о скорости ракеты как таковой: где проекции, там домножения на синусы/косинусы "и все дела".

Цитата: Les FLics от 05.11.2023 02:58:18где проекции, там домножения на синусы/косинусы "и все дела".

Вот и посчитайте.
Участок траектории за 1,37 секунды можно принять прямым отрезком.
Если ракета летит на солнце, угол между ним и направлением на солнце будет равен нулю. 
Попов бы получил скорость 0.
Посмотрите на его рисунок.

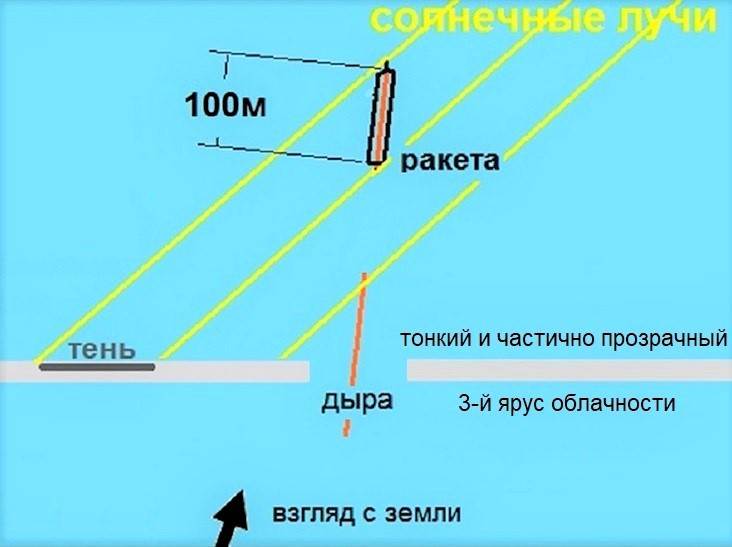
На его рисунке угол примерно 45 градусов. Умножьте на Sin 45 градусов.  
Но фактически угол был меньше, вот и получил Попов на 107-й секунде скорость 115, а не 882 м/с.
Вполне возможно, что и форма облаков внесла погрешность. Не встречал я еще облаков в виде куба или плоскости.

Цитата: Vist от 04.11.2023 00:38:19

Цитата: Михаил Бack от 03.11.2023 08:34:07Какие бы Вы речи не вели, факты  остаются фактами: чтобы создать ракетную систему для доставки людей на Скайлэб, потребовалось 15 пусков, то есть была выполнена полноценная программа лётных испытаний, 15ым пуском был выполнен пилотируемый полёт. ЭТО ФАКТ,

Нет, это не факт, а Ваше утверждение.

            Вот-вот, когда насализатору нечего сказать по существу, он просто заявляет, мол, “это не факт, тебе показалось”. Один из стандартных приёмчиков, Вы тут их щедро насыпали. И что американцы в автоматизации безнадёжно отстали от Зонда и поэтому были вынуждены жать на кнопки руками, и что вообще от СССР боялись отстать. Короче, детский сад для детей с задержкой развития – есть такие, как ни прискорбно. У вас свой придуманный мирок, в котором, к примеру, водятся “американцы” с психдефектом – они БАЯТЦА АТСТАТЬ АТ СССР. В реальном мире такое можно говорить о политическом руководстве, потому что да, проигрыш противнику по руководству стукнет. Но вот конкретно президенту Джонсону бояться было абсолютно нечего. Он просто ушёл на пенсию, даже не рыпнувшись на второй срок, и в ноябре 1968г. президентом уверенно стал Никсон.
            А за месяц до инаугурации Никсона, под Рождество, третьим пуском С5 (то есть вообще без лётных испытаний) живых людей посылают в недельный круиз вокруг луны.
            В реальном мире такое просто невозможно. Первый в истории человечества полёт к луне событие политически значимое, поэтому решение о полёте является прерогативой президента. Ну и на кой хрен Джонсону брать на себя огромный риск, санкционировать круиз с реальнейшими шансами на катастрофический итог? Поймите, ведь при успехе весь навар снимает Никсон, при неудаче – Джонсон огребает абсолютно не нужную ему кучу дерьма в виде неизбежного расследования. Для Джонсона в “рождественском круизе вокруг луны” не было ни капли смысла, это должно быть ясно даже насажополизаторам.
            И тем не менее пуск А8 был произведён.
            Это могло состояться исключительно при условии гарантированного успеха.
            А такую гарантию давал только ФАЛЬШИВЫЙ ПОЛЁТ. Этот вариант вообще был беспроигрышным. Если СССР попытается разоблачить фальшивку, это поставит крест на предвыборных обещаниях Никсона в части налаживания отношений и ему воленс-ноленс придётся продолжать политику Джонсона. Уже очень хорошо. Но были и намёки “друзей” из советского Института США и Канады, что в Политбюро КПСС настрой на “мир, дружба, жвачка” – тоже хорошо.
            Так и случилось. СССР во исполнение предательской (пора бы всем прозреть) политики КПСС поздравил США с лунным триумфом, а в советской печати изумлённые граждане узрели дорогие сердцам насажополизиторов “фотки с луны”.
            Так при содействии государства победившего пролетариата под руководством передового отряда (сиречь КПСС) американские буржуины “победили в лунной гонке”.

Цитата: Михаил Бack от 05.11.2023 09:28:15И тем не менее пуск А8 был произведён.
            Это могло состояться исключительно при условии гарантированного успеха

Не бывает гарантированного успеха в космонавтике.
Никогда вероятность успеха не равна 1.

Цитата: 3-я улица Калинина от 03.11.2023 12:50:53Беда общеобразовательной школы в том, что она дает уйму знаний, но учит применять их. 
Что постоянно упускают "опровергатели":
1. плотнтсть потока солнечного излучения на Луне около 1500 вт/м2, из них почти все приходится на видимый спектр;
2. лунный грунт отражает примернт 10%, или 150 вт/м2, в видимом - пускай 100 вт/м2;
3. общеизвестная лампа накаливания имеет КПД по видимому свету около 5%. 
 
Вывод: квадратный метр (темно коричневого) лунного грунта в видимом спектре светит как 20 (двадцать) 100 (сто) ваттных ламп накаливания.

Вообще-то меня не смущает почти белый цвет “американской луны”. Действительно, при отсутствии атмосферы и тёмно-коричневая поверхность под ярким солнышком спокойно забьёт любой прожектор и с чего бы ей выглядеть не белой. Но вот какая фигня. Я отрыл в шкафу FOOTPRINTS ON THE MOON (Associated Press, 1969), 216 страниц прекрасной полиграфии (альбом есть в сети, если интересно). На стр.190 знаменитая фота первого шага второго человека, вылезающего из курятника, расположившегося  НА РОВНОЙ БЕЛОЙ ПЛОЩАДКЕ С РОВНЁХОНЬКОЙ, ПО ЛИНЕЙКЕ, ЛИНИЕЙ ГОРИЗОНТА.

Хорошо, почему площадка белая, Вы убедительно растолковали. Маленькая просьба: растолкуйте, как в этом кадре должен выглядеть персонаж в БЕЛОМ комбинезоне? И кстати, почему-то ступеньки – они круглые, из трубок – снизу засвечены, а сверху затемнены, хотя солнышко-то вроде сверху светит, такой вот парадокс. Тоже осветите, pleeees, если не трудно.

Цитата: Сагитариус от 05.11.2023 10:34:14Не бывает гарантированного успеха в космонавтике.
Никогда вероятность успеха не равна 1.

Конгениально! Но это если не пользоваться технологиями Голливуда. А с ними - да пребудет с вами Сила Насы, доблестные джедаи!

Цитата: Sergey_64 от 05.11.2023 10:25:05Анатолий Борисович Чубайс -  наш самый выдающийся антикоммунист.

Что, завидуете его финуспехам? Ну а так-то и других персонажей не мало, к примеру, Коммунист N1 страны Хахляндии. Прекрасно уживался в ЦК КПСС.

Цитата: Михаил Бack от 05.11.2023 10:44:42FOOTPRINTS ON THE MOON (Associated Press, 1969), 216 страниц прекрасной полиграфии (альбом есть в сети, если интересно). На стр.190 знаменитая фота первого шага второго человека

Вы бы хоть фотографию показали.
Или дайте ссылочку, где можно скачать бесплатно.
Интересно, во сколько Вам обошелся этот альбом? 
И зачем, если вы считаете, что на Луну никто не летал?

Цитата: Сагитариус от 05.11.2023 11:06:18Вы бы хоть фотографию показали.
Или дайте ссылочку, где можно скачать бесплатно.
Интересно, во сколько Вам обошелся этот альбом? 
И зачем, если вы считаете, что на Луну никто не летал?

Total $17.65 eBay, с оказией приехал из-за лужи. Подарок от одного насавера.
Даты на квиточке, как ни странно, нет. Лет 10 назад.

Цитата: Михаил Бack от 05.11.2023 11:24:25Total $17.65 eBay, с оказией приехал из-за лужи. Подарок от одного насавера.

Понятно. А я не насавер, просто любитель-аполлоновед   
Ведать - знать.
Знаю, что можно и заказать отсканированное фото у НАСА, без всякой полиграфии.

Цитата: Sergey_64 от 05.11.2023 11:34:11Завидую вашей способности запрыгнуть в одну лодку с другим великим обустроителем земли русской - Александром Исаевичем Солженицыным.

Ну, на нашей ветке , ваш коллега, "полузащитник" Лисов, прекрасно сотрудничал с махровейшими иноагентами , переводил книжки наса, наговаривал на Роскосмос, работая там же. Выгнали. Но такие же "коллеги" продолжают вредить изнутри. Авгиевы конюшни вредителей. 
Леонов, известный защитник наса, банкир банка США. 
Многие "защитники" - эмигранты. США, Канада , проебалтика.
Оставшиеся - мошенники Аля зелёных котов. Собирающие деньги и сбегающие, чешущие по платным семинарам , предлагающие "скинуться" на "экспертизы" " в мутных конторах "общественных организациях", организующие "мегагалактические институты космических исследований" и позыряющие званиями самоназванных  "экспертов" этих "заведений".
Дети лейтенанта Шмидта

Цитата: Les FLics от 05.11.2023 02:58:18 Ну и, опять же, скорость ракеты в данном случае - это 3D-вектор. То, что проекция ее модуля (длины) на систему отсчета, связанную с наблюдателем, равна 115±12 м/c в данном конкретном случае ничего не говорит нам о скорости ракеты как таковой: где проекции, там домножения на синусы/косинусы "и все дела".

Вот этого было бы и достаточно. Всё, что выше - абсолютно бесполезно.
Задолбало уже скипать, иногда толковые, иногда бестолковые, рассуждения по этому поводу.
"Математикам" предлагаю рассмотреть пример в сферической системе координат. Может так станет ясно, что проекция всегда даст составляющие скорости только по двум координатам (в данном случае - по угловым), а в пространстве их три. Линейную составляющую, в сферических координатах, тень на облаках не даёт. А она есть и весьма существенна.
Если и это не поможет,  то "эта музыка будет вечной". Надо выдёргивать батарейки...

Цитата: RusBelS от 05.11.2023 12:17:51Леонов, известный защитник наса, банкир банка США. 
Многие "защитники" - эмигранты. США, Канада , проебалтика.

Леонов не защитник НАСА, и никуда не уехал. 
Не уехали и другие космонавты.

Цитата: Сагитариус от 05.11.2023 12:27:23Леонов не защитник НАСА, и никуда не уехал. 
Не уехали и другие космонавты.

Сколько раз соврал космонавт-банкир Леонов только в одном своём интервью?
https://photo-vlad.l…99924.html
 
Чернуха, но факты интересные весьма...
https://igor-mikhayl…30023.html

Цитата: Михаил Бack от 05.11.2023 10:44:42Хорошо, почему площадка белая, Вы убедительно растолковали. Маленькая просьба: растолкуйте, как в этом кадре должен выглядеть персонаж в БЕЛОМ комбинезоне?

Как персонаж в белом, только скафандре. Альбедо скафандра всяко выше альбедо поверхности.

Цитата: Михаил Бack от 05.11.2023 10:44:42И кстати, почему-то ступеньки – они круглые, из трубок – снизу засвечены, а сверху затемнены, хотя солнышко-то вроде сверху светит, такой вот парадокс. Тоже осветите, pleeees, если не трудно.

Солнышко, хоть и сверху, но ступеньки в тени от модуля. Подсвечиваются только отраженным светом от поверхности, которая снизу. Никаких парадоксов.

Цитата: RusBelS от 05.11.2023 12:38:35Сколько раз соврал космонавт-банкир Леонов только в одном своём интервью?
https://photo-vlad.l…99924.html
 
Чернуха, но факты интересные весьма...
https://igor-mikhayl…30023.html

Базар-вокзал на желтых страницах блогеров не интересен.
Плохи дела у этих блогеров, мал читательский интерес, хоть и рекламируете их усердно.