О цвете Луны
26 фев 2020 в 22:54
sharp89
|
|---|
Цитата: viewer от 26.02.2020 09:58:16Какого цвета будет объект В вопросах цветам вам, опровергам, изрядно подкузьмил некий доцент Коновалов, как ни странно  Со своими опытами с пластелином. Со своими опытами с пластелином. Напомню, что он вылепил и какие намерял графики спектра:  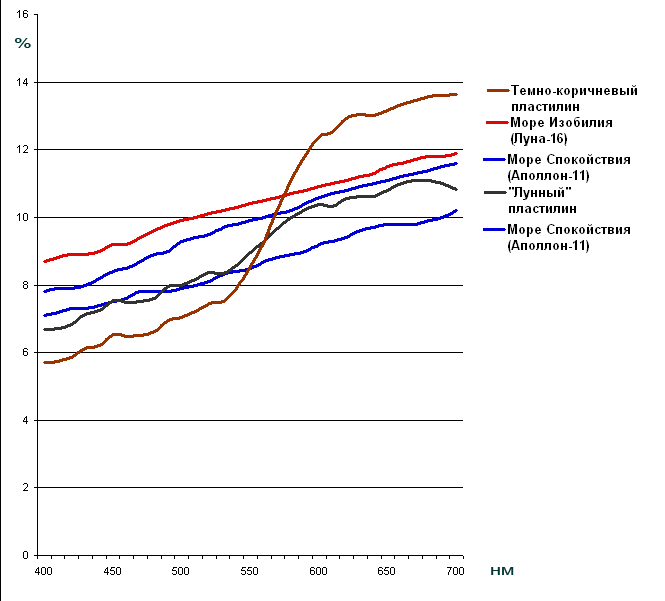 Несложно заметить две вещи: Во-первых, полученный "лунный" пластилин уже довольно сложно называть коричневым, особенно если в качестве эталона коричневого у нас пластилин, расположенный по центру. Во-вторых, даже такой слабо-коричневатый пластилин имеет более насыщенный цвет, чем образцы Луны-16 и Аполлона-11, потому что разность отражения в синей и красной зоне у него больше, чем у лунных образцов. То есть, чтобы получить полное соответствие с одним из образцов, Коновалову следовало еще сильнее понижать насыщенность. Почему он этого не сделал, неизвестно - возможно, результат получался совсем уж неудовлетворительный.  Но можно сделать это в графическом редакторе, получая примерно следующее: Но можно сделать это в графическом редакторе, получая примерно следующее:  Некоторая краснота всё еще видна, если приглядываться или тыкать пипеткой. Но в целом, если с грунтом именно таких оттенков учёные (в том числе советские) имели дело, нет ничего удивительного, что его часто характеризовали именно как темно-серый или черноватый, далеко не всегда отмечая присутствующие в нём красноватые оттенки. Притом, что формально, по приборам, преимущество красного, конечно, фиксируется. Отсюда вытекают и столь разные оттенки Луны на разных фото: цвет крайне слабо выраженный, и небольшое смещение в одну сторону сделает его полностью серым, а в другую - заметно коричневым. При этом колебания цветов других объектов, хотя тоже имеют место, но на невооружённый взгляд не так заметны. То же самое и с визуальным наблюдением: даже индивидуальная разница в цветовосприятии может влиять на воспринимаемый цвет, не говоря о светопропускании стекол, через которые ведется наблюдение, местоположении Солнца и наблюдателя, расстоянии до Луны итд. Собственно, ещё задолго до космической гонки отмечалась разница в восприятии цвета Луны разными людьми:  Так что либо козни и заговоры "серомунистов" против "буромунистов" уходят глубоко в прошлое, либо, что более вероятно - такие разночтения в восприятии цвета Луны как раз-таки закономерны по вышеизложенным причинам. Отредактировано: sharp89 - 26 фев 2020 в 22:54
|
|
|
ОТВЕТЫ (963)
|
|
viewer ( Слушатель ) |
| 27 фев 2020 в 06:57 |
- ...
Цитата: sharp89 от 26.02.2020 22:54:01
Сынок!
Ты вместо того чтобы свою столь неуклюжую чернокобелеотмывку тут надрачивать взял бы да привёл и ПЕРЕВЁЛ фрагмент текста, который идёт после адренковской таблички и который ты так хитро (как тебе мнится) обчекрыжил.
Только сдаётся мне, что ты этого ни в жисть не сделаешь, в твою задачу вонять за НАСУ это не входит.
- +0.12 / 18
-
|
|
BomBarDir ( Слушатель ) |
| 27 фев 2020 в 08:55 |
- ...
Цитата: sharp89 от 26.02.2020 22:54:01
Самое интересное в том, что цвета не существует в природе. Тем более коричневого. Ещё интереснее тот факт,что все споры о цвете на экранах мониторов ни о чём,потому как на них RGB цвета, т.е. не дисперсный спектр. А Виювер просто занимается демагогией.
- -0.17 / 19
-
|
|
viewer ( Слушатель ) |
| 27 фев 2020 в 09:26 |
- ...
Цитата: BomBarDir от 27.02.2020 08:55:22
Дык не только цвета - если

PS И самой природы тоже не существует.

- +0.09 / 16
-
|
|
sergevl ( Слушатель ) |
| 27 фев 2020 в 15:02 |
- ...
Цитата: BomBarDir от 27.02.2020 08:55:22
У тебя в мониторе РГБ цвета только потому что у тебя глаза работают в РГБ-системе.
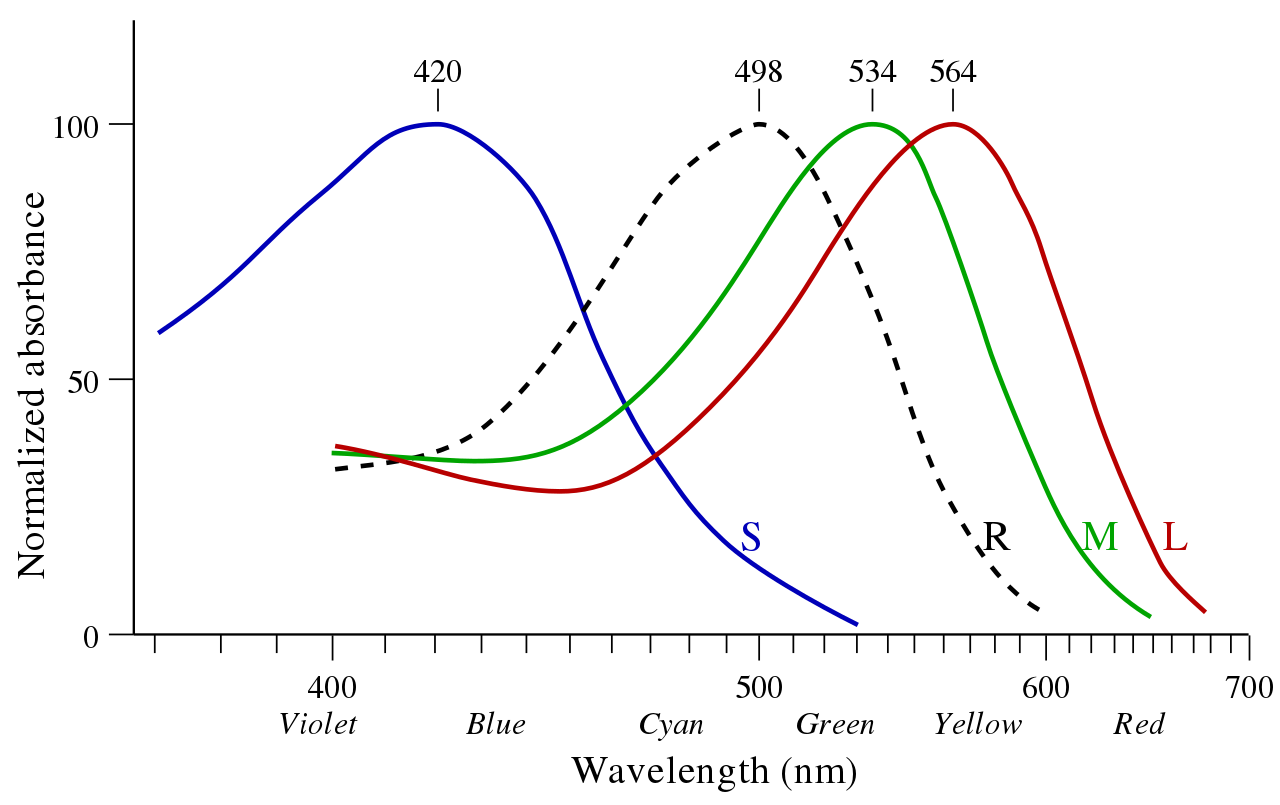
А ты этого не понимаешь, и пишешь чушь.
- +0.05 / 15
-
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 15:07 |
- ...
Цитата: sergevl от 27.02.2020 15:02:46
Чего?!
Цитата: sergevl от 27.02.2020 15:02:46
Чушь сейчас написали вы. Просто дичайшую чушь.
- -0.07 / 11
-
|
|
sergevl ( Слушатель ) |
| 27 фев 2020 в 15:23 |
- ...
Цитата: Pаssаt от 27.02.2020 15:07:34
Это не я писал, википедия. А она чушь писать не может - только чистейшую истинную кристальную правду.
Ведь только тупые конспирологи думают, что википедия может обманывать. )))) А ты ведь на стороне силы правды, википедии, британской энциклопедии и прочих святых текстов. Ну что опровергай свою библию. )))
ЦитатаВ сетчатке глаза человека есть три вида колбочек, максимумы чувствительности которых приходятся на красный, зелёный и синий участки спектра[3]. Ещё в 1970-х годах было показано, что распределение типов колбочек в сетчатке неравномерно: «синие» колбочки находятся ближе к периферии, в то время как «красные» и «зелёные» распределены случайным образом[4], что было подтверждено более детальными исследованиями в начале XXI века[5]. Соответствие типов колбочек трём «основным» цветам обеспечивает распознавание тысяч цветов и оттенков. Кривые спектральной чувствительности трёх видов колбочек частично перекрываются, что способствует явлению метамерии. Очень сильный свет возбуждает все 3 типа рецепторов, и потому воспринимается, как излучение слепяще-белого цвета (эффект метамерии).
https://ru.wikipedia.org/wiki/%D0%97%D1%80%D0%B5%D0%BD%D0%B8%D0%B5_%D1%87%D0%B5%D0%BB%D0%BE%D0%B2%D0%B5%D0%BA%D0%B0
- +0.15 / 14
-
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 15:42 |
- ...
Цитата: sergevl от 27.02.2020 15:23:56
Вот только еще вам понять бы, о чем там написано.
Спектральная чувствительность глаза такая
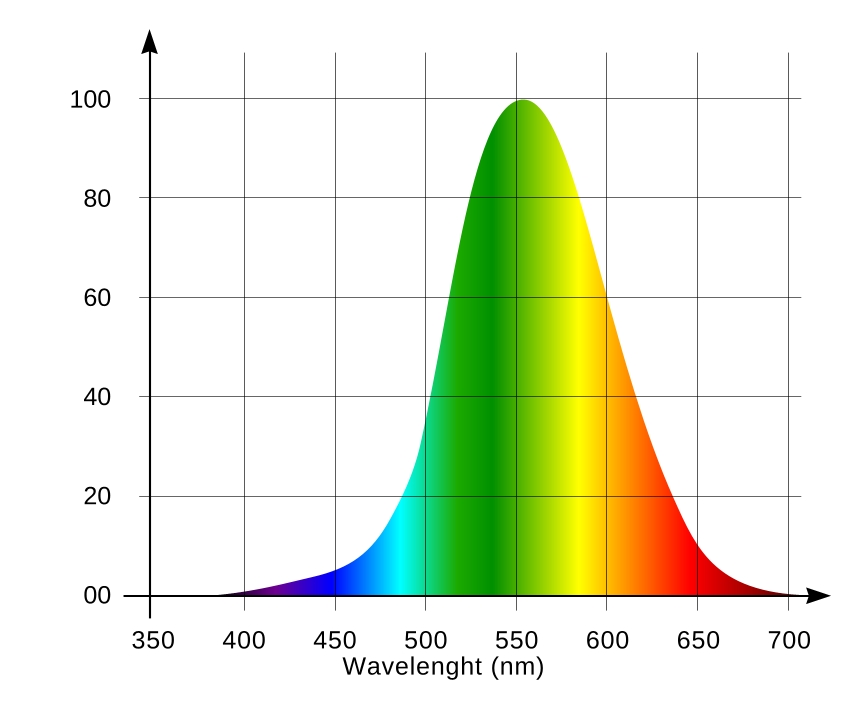
Спектральная характеристика монитора такая

Одно и то же, да?
Глаз воспринимает весь видимый спектр без разрывов. Монитор воспроизводит только три небольших участка из этого спектра.
Глаз человека способен воспринять, к примеру, монохромный желтый цвет. Монитор воспроизвести монохромный желтый цвет не в состоянии.
- -0.08 / 13
-
|
|
sergevl ( Слушатель ) |
| 27 фев 2020 в 16:33 |
- ...
Цитата: Pаssаt от 27.02.2020 15:42:51
Ты привел график чувствительности родопсина. И то сдвинул зачем то его вправо. А за цветовое зрение отвечают три пигмента
йодопсина.
https://ru.wikipedia.org/wiki/%D0%99%D0%BE%D0%B4%D0%BE%D0%BF%D1%81%D0%B8%D0%BD
Сам подумай, как ты поделишь цвет на каналы если у тебя чувствительность идёт одним максимумом для желтого цвета?
Читай до посинения до отупения википедию, а не опровергай ее! Это твоя библия! Там написано что летали - и ты должен не опровергать википедию, а наоборот с ересью бороться. )))
- +0.17 / 18
-
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 20:04 |
- ...
Цитата: sergevl от 27.02.2020 16:33:14
Не тебе мне говорить, что я должен, а что нет. И я не опровергаю википедию. Вот тебе картинка с вики с подписью

Глаз воспринимает ВЕСЬ спектр видимого света без разрывов. А монитор воспроизводит только малую часть этого спектра.
- -0.03 / 11
-
|
|
sergevl ( Слушатель ) |
| 27 фев 2020 в 21:02 |
- ...
Цитата: Pаssаt от 27.02.2020 20:04:08
Принцип такой что для каждого пигмента есть свой диапазон поглощения - то есть цвет.
К примеру, хлорофилл зеленый потому что поглощает синие и красные лучи сильней, чем зеленые. А отражает зеленые.
Точно также разные пигменты в глазу поглощают разные спектральные диапазоны.
Есть животные с двух, трёхдипазонными пигментами. Есть животные с 10 диапазонами.
- +0.16 / 9
-
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 21:21 |
- ...
Цитата: sergevl от 27.02.2020 21:02:07
И? А еще дальтоники бывают. Дальше то что? Все типы колбочек сетчатки в общей сложности способны поглотить ВЕСЬ спектр видимого цвета. От и до. Без разрывов. В соответствии с тем графиком, что я тебе показал.
Монитор воспроизводит лишь три маленьких кусочка из этого спектра.
Так что, здесь
Цитата: BomBarDir от 27.02.2020 08:55:22
Абсолютно верно сказано.
А ты, уравнивая глаз и монитор, пишешь чушь.
- -0.13 / 16
-
|
|
sergevl ( Слушатель ) |
| 28 фев 2020 в 00:38 |
- ...
Цитата: Pаssаt от 27.02.2020 21:21:59
Ты не понял ничего) почему ты видишь на экране монитора много цветов? Да потому что цветоразностные рецепторы у тебя в глазу наиболее чувствительны именно к тем участкам спектра, которые излучает монитор. Пиксели в мониторе подобраны под спектры поглощения светочувствительных клеток твоих глаз.
Мало того под эти спектры поглощения подобраны пзс матрицы в камерах, эмульсии в цветных плёнках.
Таким образом достигается достоверная цветопередача. А мозг сравнивает силу сигнала от разных типов клеток, и на основе этого закрашивает образ в тот или иной цвет. То есть чтобы обмануть рецепторы создают ргб систему.
На самом деле можно увидеть и жёлтый монохроматический цвет, но я это не отрицал на графиках трёх полос чувствительность глаза есть в жёлтом спектре, только глаз и мозг умеют подумывать, аппроксимировать жёлтый цвет видя одновременно Красный и зелёный.
- +0.20 / 16
-
|
|
Pаssаt ( Слушатель ) |
| 28 фев 2020 в 09:21 |
- ...
Цитата: sergevl от 28.02.2020 00:38:00
Потому что у человека такое цветовосприятие.
Цитата: sergevl от 28.02.2020 00:38:00
Неверно.
Просто посмотрев на эти графики, понятно, что спектр пикселей монитора не совпадает с максимумами спектральной чувствительности глаза.


Такая система выбрана потому, что используя именно эти три основных цвета можно охватить максимум из цветового пространства, доступного глазу при минимуме базовых цветов. При этом, цветовой охват этой схемы намного меньше цветового охвата глаза. И повысить его можно только добавляя дополнительные базовые цвета. Но это будет уже другая цветовая схема.
Цитата: sergevl от 28.02.2020 00:38:00
Ага, точно. Вот только непонятно, чего же это люди мучаются со всякими LAB, CMYK, калибровкой экранов, принтеров, сканеров и прочей херотой? Там не все так просто.
Цитата: sergevl от 28.02.2020 00:49:10
А зачем обманывать глаз, если, по твоему, он с монитором и так одинаковый?
Цитата: sergevl от 28.02.2020 00:49:10
Сам же пишешь, глаз воспринимает желтый спектр. Монитор его не воспроизводит.
Монитор не в состоянии передать все цвета, которые может увидеть глаз. Глаз воспринимает весь спектр, монитор воспроизводит три маленьких кусочка. И спектральная характеристика объекта и изображения этого объекта на экране - это две огромные разницы. О чем тебе и говорят. Так что уравнивать монитор и глаз некорректно. И тем более неправильно спектральной характеристикой луны тут размахивать, глядя на изображения в мониторе.
Но я надеюсь, ты понял, наконец, что цвет - это субъективная характеристика. И расскажешь про это своим коллегам.
- -0.19 / 19
-
|
|
чебуратор ( Слушатель ) |
| 28 фев 2020 в 11:53 |
- ...
Цитата: Pаssаt от 28.02.2020 09:21:24
Мощный перл. Отлить в граните.
Здоровые люди воспринимают цвета одинаково.
Слышите, уважаемый? ОДИНАКОВО
Про таблицы Рабкина вам известно что-нибудь?
Как же радуют эти специалисты по натягиванию совы на глобус ))
Пишите больше и чаще в этой ветке.
- +0.21 / 20
-
|
|
Pаssаt ( Слушатель ) |
| 28 фев 2020 в 13:08 |
- ...
Цитата: чебуратор от 28.02.2020 11:53:12
Сами же пишите - люди воспринимают. Цвет - это вопрос восприятия.
Как забавно выглядят те, кто с умным видом рассуждают на темы, которые не понимают. Даже глаза одного человека воспринимают цвет по разному.
Есть объективная физическая характеристика объекта - спектральная. А есть субъективная характеристика - то, как воспринимается спектр объекта. Объекты с разными спектральными характеристиками при одинаковых условиях наблюдения могут восприниматься, как объекты одинакового цвета. А объекты с одинаковой спектральной характеристикой при различных условиях наблюдения могут восприниматься, как объекты разного цвета.
- -0.13 / 17
-
|
|
sharp89 ( Слушатель ) |
| 28 фев 2020 в 13:13 |
- ...
Цитата: чебуратор от 28.02.2020 11:53:12
У меня дома есть пластиковая ваза для фруктов, которую половина людей считает скорее зеленой, а другая половина - скорее желтой. Какая половина из этих людей нездорова, стесняюсь спросить?

Самое забавное, что и на фото, в зависимости от минимального изменения настроек камеры и характеристик экрана, на котором просматривать, она будет либо более зеленой, либо более желтой.
- -0.05 / 18
-
|
|
Technik ( Слушатель ) |
| 31 мая 2020 в 08:56 |
- ...
Цитата: Technik от 31.05.2020 08:42:55
4. Ролик https://youtu.be/PdSm27BjoUg
Приговор, видите ли, роверу. Тот самый, который просил прокомментировать ув. ДядяВася.
Наиболее существенные моменты.
0.40 и далее. Доставляют претензии к точке съемки – согласно хотелке г-на ING, Чарльз Дьюк с камерой наперевес должен был бежать за ровером (на ровере был Джон Янг, о чем говорят командирские красные полоски на скафандре и на шлеме).
1.05 и далее – определение скорости ровера. Это, конечно, мощно – для доказательства того, что ровер ездил на Земле, использовать снимки LRO – однозначно подтверждающие поездки по Луне. Те самые, которые "...на снимках LRO – подделка» . Напомнить бы автору про трусы и крестик – но он не поймет…
К тому же некорректно определять среднюю скорость на всем показанном в ролике пути ровера, поскольку имел место разворот – на котором скорость снижена. Поэтому полученное ING значение 2 м/сек неверно.
Правильнее определять скорость на отрезке пути с равномерным движением ровера – что в свое время и было сделано, и для дальнейших расчетов было получено значение 2,7 м/сек – т.е сразу на треть большее, чем у ING.
2.40. ING не понимает, что высокие выбросы пыли вызваны именно пробусовкой колес по той причине, что инерционность движителя (электромотор – волновой редуктор – колесо) ровера минимальна, и как только сцепление с поверхностью ослабевает, скорость вращения колеса увеличивается практически мгновенно. Говорить же об «инерции ротора электромотора» в данном случае вообще не приходится, аналогия с «инерционными автомобильчиками» здесь неприменима. По той причине, что у инерционных автомобильчиков всегда имеется маховик, накапливающий энергию, а потом отдающий ее на привод колес.
03.35 и далее, оценка направления и скорости, с которой могут вылетать из-под колеса частицы пыли.
Нужно отметить, что ING – возможно, с подсказки г-на Попова – рассматривает поведение выбрасываемой колесами ровера пыли более строго, а именно с учетом движения ее частичек по циклоиде, чем если рассматривать их движение упрощенно, только как результат вращательного (без учета продольного движения) колеса.
Но правильность вывода ING о том, что пыль должна выбрасываться в направлении движения ровера, а не назад – каждый может оценить, посмотрев несколько кадров ролика c ровером. Где пыль благополучно вылетает в сторону, противоположную движению.
Происходит это по той причине, что частички пыли по-разному прилипают к колесу ровера, и часть их выбрасывается центробежной силой, возникающей при вращении колеса, с разных точек колеса. При этом на максимальную высоту вылетают согласно этому рисунку только те частички, что на границе, определяемой пылезащитным щитком – т.е. под углом ϕ, определяемым конструкцией щитка. Как было установлено, он составляет примерно 45°, для расчета было принято 50°.

ING не учитывает тот очевидный факт, что частицы пыли, оторвавшиеся после этих 50°, хотя и полетят вперед – по продольному движению колеса – но будут задержаны щитком, и никакого выброса пыли вперед по движению не будет, за исключением боковин колеса там, где они не прикрыты щитком, или вперед-вниз (как на фото из разбора ролика 1). Здесь V л.вр. – линейная скорость линейная скорость вращательного движения, равная скорости продольного движения колеса.
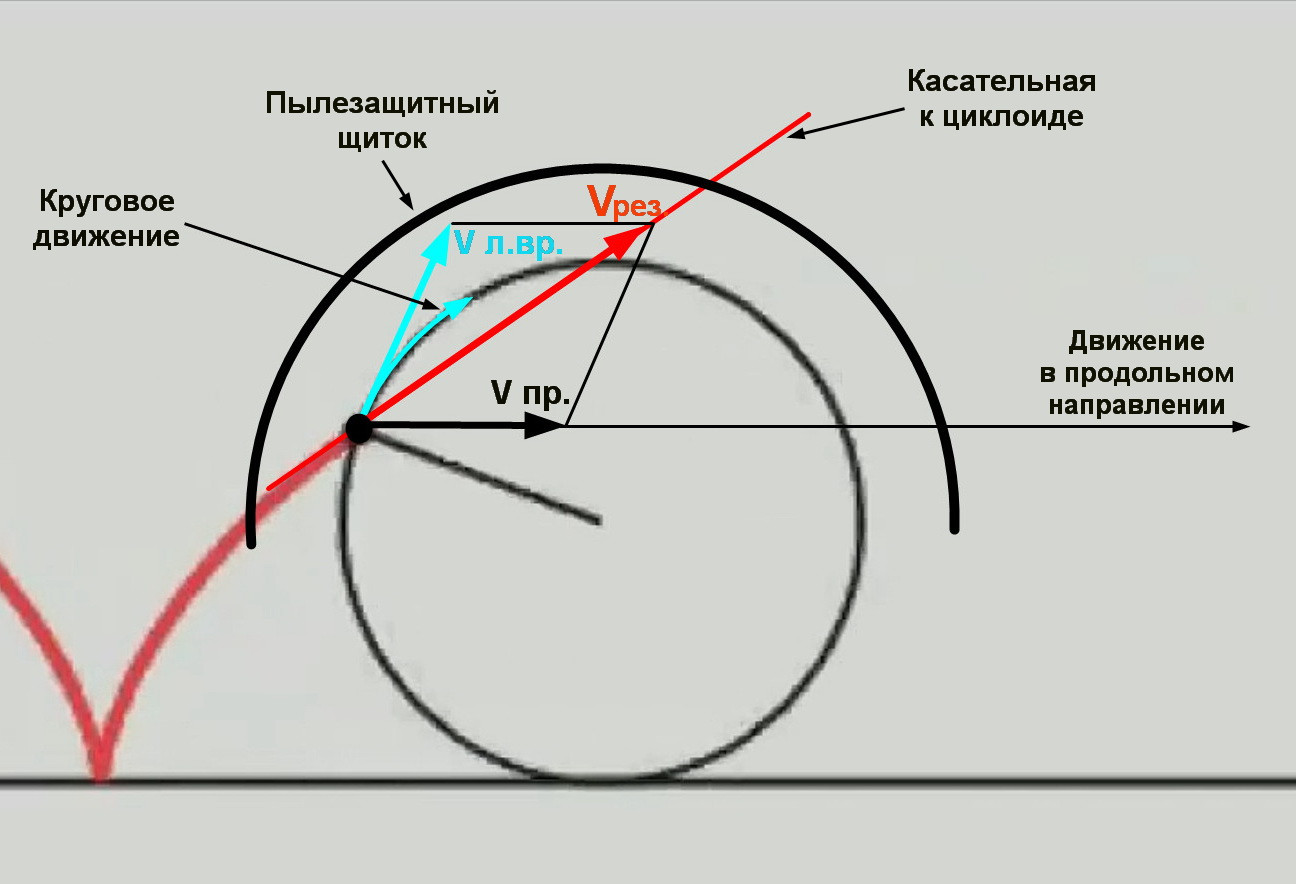
Как известно, если тело участвует одновременно в нескольких движениях, то в общем случае каждое из них совершается независимо от остальных. И что вектор его скорости можно разложить на составляющие по любым двум осям.
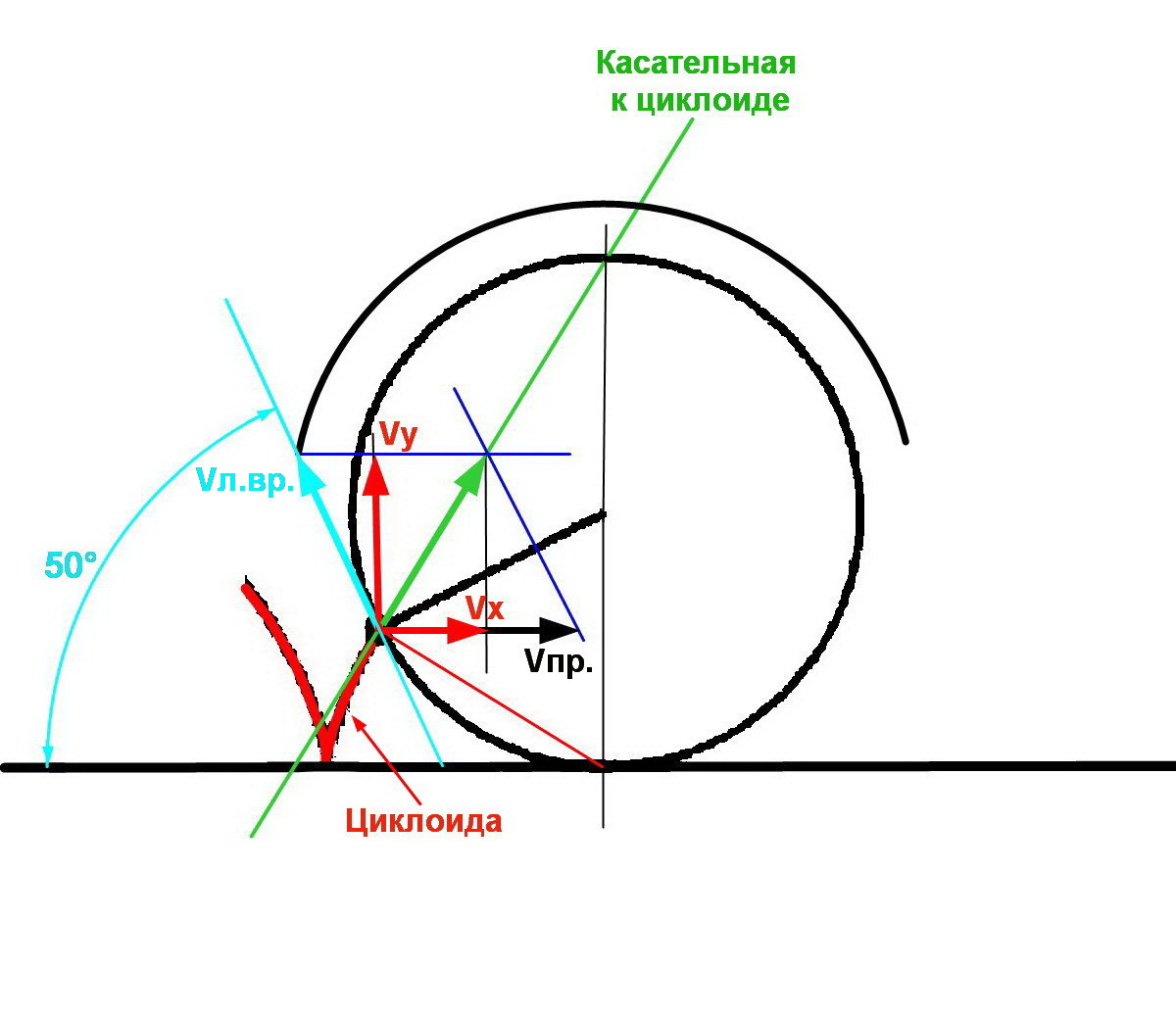
Из этого рисунка очевиден интересный момент – продольная скорость Vx движения частички пыли, вылетевшей под углом 50° к горизонту, т.е. к направлению продольного движения колеса, – будет меньше скорости его РАВНОМЕРНОГО продольного движения Vпр. – т.е. пыль будет отставать от ровера. А вот когда ровер тормозит, да еще и с некоторым заносом – тогда и наблюдаются массивные выбросы пыли вперед по движению – пыль обгоняет тормозящий ровер.
Дешевенький стеб ING на тему того, по какой такой причине передний щиток длиннее заднего - «…американцы любят пустить пыль повыше…» - еще одно свидетельство того, что у персонажа соображалка работает неважно. А почему это именно так – предоставляю решить этот реГбус-кроКсворд читающим этот пост.
При этом совершенно непонятно, зачем на 6.50 приведен расчет высоты выброса при скорости ровера 2 м/сек (1,13 м/сек), когда через минуту ING сам же приводит более правильное значение скорости, те самые 2,7 м/сек.
А при скорости 2,7 м/сек высота выброса даже по методике самого ING составит 1,89 метра – что, понятно, его категорически не устраивает, так как на Земле такая высота при этой скорости ровера невозможна от слова совсем.
В ходе дальнейших рассуждения о высоте и скорости выброса пыли «с помощью подсчета кадров» (с 7.00) ING неверно посчитал кадры ролика «Grand Prix», в течение которых происходит подъем пыли на высоту 0,53 метра. У него это 11 кадров, в «Grand Prix» - 14-15 при скорости 30 кадров в секунду (для сомневающихся можно сделать соответствующее «скрин-шоу», не привожу его исключительно из экономии места.)
Но для начала - расчет по его данным – но при «лунном» ускорении свободного падения.
1. Высота подъема тела, брошенного вертикально вверх:
Н = Vo × t – a × t2 / 2.
При полной высоте подъема 0,53 метра за время 11/30 (0,367 сек) и а = 1,62 м/сек2, Vo = 1,74 м/сек. Далее обозначена как V1.
2. Для определения начальной скорости выброса пыли колесом, с кадра 7.44 ролика ING сняты необходимые для расчета размеры:
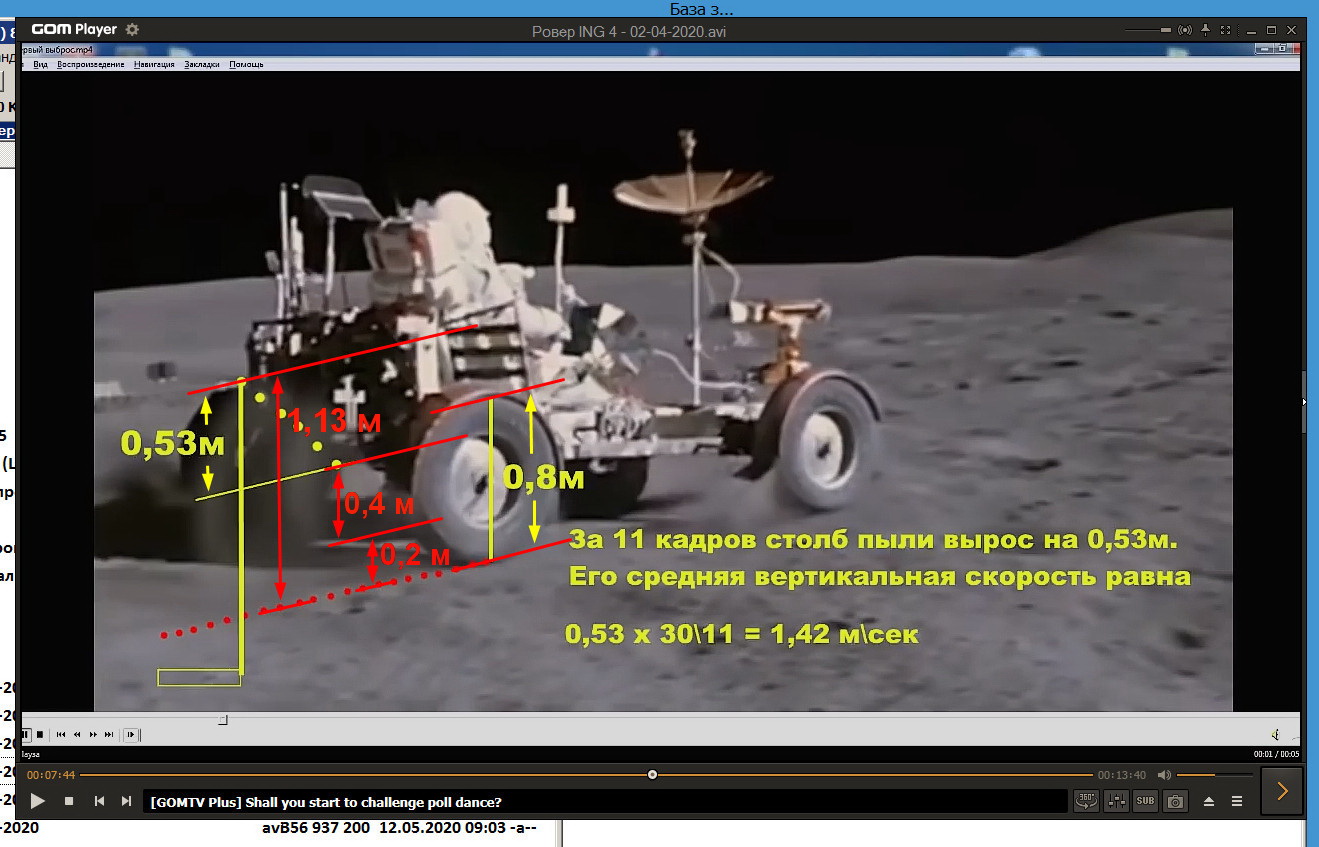
С учетом его же «добавки» в 0,2 метра («четверть высоты колеса»), длина траектории до точки, где скорость равна 1,74 м/сек – 0,4 метра. Ниже схема для расчета.
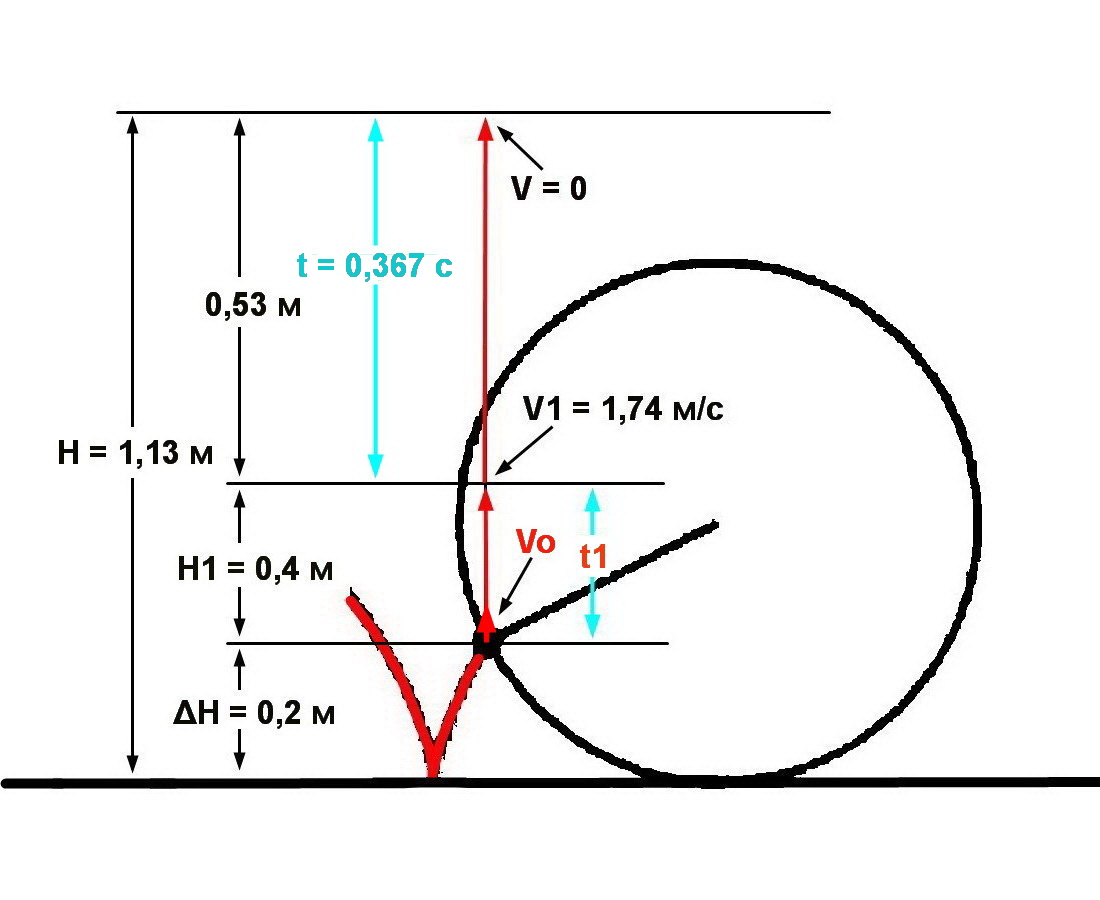
3. Для определения начальной вертикальной скорости Vo была составлена система уравнений:
H1 = Vo × t1 - a × t12 /2
V1 = Vo - a × t1,
где: H1 = 0,4; V1 = 1,74; a = 1,62; t1 – время подъема с начальной высоты ΔH на высоту H1 ,
которая сводится к квадратному уравнению с неизвестным t1 :
t12 + 2,15t1 – 0,49 = 0.
Решение системы - t1 = 0,21 сек, Vo = 2,08 м/сек, что для угла выброса в 60° дает скорость выброса с колеса 2,40 м/сек, никаких 3,26, насчитанных ING, и в помине нет.
Если же за основу взять подъем на высоту 0,53 метра за 14 и 15 кадров, тогда: V1 = 1,51 м/сек при 14 кадрах, V1 = 1,46 м/сек при 15-ти.
Соответственно Vo = 1,89 и 1,85 м/сек, а скорость выброса с колеса – 2,18 и 2,14 м/сек.
При этом расчетная полная высота подъема при этих Vo равна 1,30 и 1,25 метров, что достаточно близко к определенной на кадре 7.44 ролика ING (1,13 метра, см. выше скрин кадра 7.44).
Так что не в «погрешностях измерения" (© ING) дело, а в стремлении г-на ING подогнать результат под заранее заданное «они не летали!!!» - что исключает желание по-настоящему разобраться в материале.
При таком заезде на Земле (т.е. при выбросе пыли на высоту 1,13 метра на Земле), Vo = 4,4 м/сек, а скорость выброса с колеса – 5,7 м/сек. Что дает скорость ровера в 20,5 км /час. Возможность такой скорости на таком рельефе, что в ролике, а также разумность утверждений об ускоренно-замедленной съемке, предлагаю оценить г-дам оппам самостоятельно.
Все последующие «разоблачения» ровера г-ном ING путем определения ускорения свободного падения через неверно определенную максимальную скорость выброса пыли дают и неверный результат.
В разбираемом ING эпизоде с подъемом пыли на отрезке 0,53 метра (1.38 самого «Grand Prix») от отрыва от колеса до максимальной высоты (1,13 метра) - 19 кадров, т.е. 0,63 сек. При скорости ровера 2,7 м/сек вертикальная скорость подъема пыли Vy = Vл.вр. × cos 40° = 2,05 м/сек. Начальная высота подъема пыли, как было ранее определено, 0,14 метра, тогда высота подъема от точки колеса до максимума H = 0,99 м.
Из формулы H = Vo × t – a × t2/2 ускорение а = 1,51 м/сек2. Лунное «а», напомню, 1,62 м/сек2. Ч.И.Т.Д.
В качестве еще одной иллюстрации взят момент 2.31 «Grand Prix». Три последовательных кадра показывают начало роста, середину и остановку выброса пыли – но здесь имела место пробуксовка колеса, что видно по массивному выбросу пыли на первом кадре.



От начала выброса до остановки – примерно 30 кадров, т.е. 1 секунда. Высота выброса, как видно на третьем кадре, несколько больше двух диаметров колес, принимается 1,8 м.
Решение обратной задачи – по высоте выброса определить мгновенную скорость вращения колеса, приведшую к такому выбросу - дает Vл.вр.= 3,03 м/сек. Тогда скорость вращения колеса – 1,2 оборота в секунду. Нормальная, без пробуксовки, при скорости 2,7 м/сек – 1,08 в секунду. Как очевидно, ничего сверхъестественного в таком увеличении скорости вращения колеса нет.
В заключение отмечу конечный вывод г-на ING, он просто гениален – «Как же удалось фокусникам из НАСА поднять пыль от медленных колес на столь большую высоту? Вывод однозначный - каким бы способом это ни было бы сделано, но ролик является подделкой». Почему-то вспомнилась незабвенная Псаки – «…я не знаю точно, в чем там дело, но виновата Россия».
И это еще не все, коллеги...
- +0.20 / 21
-
|
|
ДядяВася ( Слушатель ) |
| 27 фев 2020 в 21:09 |
- ...
Цитата: Pаssаt от 27.02.2020 15:42:51
Не путайте цвета отдельных пикселей монитора и цвета, которые может отобразить монитор.
- +0.22 / 15
-
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 21:26 |
- ...
Цитата: ДядяВася от 27.02.2020 21:09:58
О! Я то не путаю. Я уже неоднократно говорил, что нет прямой связи между спектром и цветом.
А вот Вьювер, тряся своей спектральной характеристикой, не в состоянии понять, что спектральная характеристика Луны на фотографиях ну совсем никак не похожа на его картинку.
- -0.13 / 16
-
|
|
BomBarDir ( Слушатель ) |
| 27 фев 2020 в 21:54 |
- ...
Цитата: sergevl от 27.02.2020 15:02:46
Вот она...жертва Педивикии. А чо тогда в РГБ системе нельзя воспроизвести некоторые цвета, например чисто синий или жёлтый? А глаз их видит. Да, и кроме того РГБ модель не работает на бумаге, а глаз видит всё что отражает свет.
И ещё,РГБ модель работает только на излучающих источниках. А у человека глаза не светются.Такая вот пичалька. Бггг.

- -0.14 / 16
-
|
|
sergevl ( Слушатель ) |
| 28 фев 2020 в 00:49 |
- ...
Цитата: BomBarDir от 27.02.2020 21:54:12
Ргб модель это самый экономичный способ обмануть глаз)
Можно сделать на каждый нанометр спектра свой пиксель. И сделать систему из 500 различных монохроматичных полос. Добавь в ргб систему жёлтый пиксель и не парься. Но. Свет из него будет поглощаться как красночувствительным так и зеленочувствительными клетками. И сравнивая сигнал с двух типов рецепторов, глаз и мозг будут знать: это жёлтый цвет. Тоже самое пусть не так красочно получается приодновременном свечении красного и зелёного.
- +0.25 / 18
-
|
|
BomBarDir ( Слушатель ) |
| 28 фев 2020 в 10:42 |
- ...
Цитата: sergevl от 28.02.2020 00:49:10
Ёптыть... вот это заезд!
Это самый оптимальный способ кодирования цветовых оттенков, при минимуме основных цветов, и упрощения конструирования аппаратного обеспечения.
ЦитатаМожно сделать на каждый нанометр спектра свой пиксель.
Зачем из собаки делать человека, если его может родить любая баба?
ЦитатаИ сделать систему из 500 различных монохроматичных полос.
Ты бы осетра урезал бы. А то стоимость конечной аппаратуры будет неподъёмной, а преимуществ у неё не будет никаких.
ЦитатаДобавь в ргб систему жёлтый пиксель и не парься.
Брось читать Педивики. Невозможно в этой модели получить монохромный жёлтый и синий цвет. Теоретически невозможно. Математика не позволяет.
Цитата]Но. Свет из него будет поглощаться как красночувствительным так и зеленочувствительными клетками. И сравнивая сигнал с двух типов рецепторов, глаз и мозг будут знать: это жёлтый цвет. Тоже самое пусть не так красочно получается приодновременном
свечении красного и зелёного.
Ты совсем не понимаешь чего несешь...ты так договоришься до Нобелевки.
Давай лучше вернёмся к нашим баранам. Как все твои экзерсисы доказывают Апупею? Ды никак.

- -0.10 / 16
-
|
|
sharp89 ( Слушатель ) |
| 27 фев 2020 в 11:30 |
- ...
Цитата: viewer от 09.02.2020 11:57:49
Замечательная фотка. Невооруженным взглядом видно, что полутеневые участки на скафандре имеют нездоровый зеленовато-голубоватый оттенок
 То же и с белым на флаге - вся полутень зеленоватая.
То же и с белым на флаге - вся полутень зеленоватая. Разумеется, флаги и скафандры следует с осторожностью использовать в качестве цветовых эталонов, но данный случай довольно очевидный, и посторонняя аквамариновая расцветка слишком уж явно выражена.
Что будет, если подровнять немного?

- -0.10 / 14
-
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 12:26 |
- ...
Цитата: sharp89 от 27.02.2020 11:30:50
Внезапно может получиться что нибудь подобное этому )))

- -0.08 / 15
-
|
|
viewer ( Слушатель ) |
| 27 фев 2020 в 13:31 |
- ...
Цитата: Pаssаt от 27.02.2020 12:26:03
Да если бы!

На самом деле вот что получается

вот из этого!


Причём тот, кто цементоид, приведённый к пресловутому neutral grey'ю
These scans are being done by NASA Johnson, with some post-processing by Kipp Teague. The film is scanned at 4096 x 4096 pixels per image. (See a discussion from Arizona State University about the scanning process.) Kipp reduced each digital image to approximately 2350 x 2350 pixels (equivalent to 300 dpi) and did minor adjustments of levels to ensure that (1) brightly lit areas of lunar soil were neutral grey, (2) objects with known colors (such as the CDR stripes or the LCRU blankets) looked right, and (3) information in bright or dark areas was not lost
Киппом (Тэйгом) были проделаны некие незначительные подстройки уровней, чтобы гарантированно были удовлетворены все три условия:
(1) Освещённые места на лунном грунте имели нейтрально серый цвет.

(2) Объекты с хорошо известным известным цветом - командирские нарукавные полосы

или плёнка теплозащитного покрытия

имели естественный цвет.
(3) Отсутствие потери детализации в светах и в тенях.
покрасил в умопомрачительный гнило-свекольный цвет был никто иной как этот же самый Кип Тэйг, собственно персоной!

Это лилово-бурое uyobishche выложено на его личной страничке на сайте самой НАСЫ - http://history.nasa.…s/5946.jpg
КАПЕЦ просто!

- +0.23 / 18
-
|
|
viewer ( Слушатель ) |
| 27 фев 2020 в 12:36 |
- ...
Цитата: sharp89 от 27.02.2020 11:30:50
Ты лучше цвет засыпки съёмочной площадки подровняй, чтобы она хоть чуть-чуть соответствовала описанию цвета Моря Спокойствия ()Mare Tranquillitatis)

в исполнении доблестных ироеф А-10


- +0.19 / 17
-
|
|
sharp89 ( Слушатель ) |
| 27 фев 2020 в 12:43 |
- ...
Цитата: viewer от 27.02.2020 12:36:20
"Подравниваться" должна вся фотография целиком. Потому что если мы видим зеленую синеву там, где её точно не должно быть, это значит что вся фотография с избытком синего и зеленого. Сам догадаешься, что будет если из нейтрально серого вычесть немного зеленого и синего?
- -0.10 / 19
-
|
|
Удаленный пользователь |
| 27 фев 2020 в 17:08 |
Сообщение удалено
лателеннолоппа
02 мая 2020 в 19:28
лателеннолоппа
02 мая 2020 в 19:28
Отредактировано: лателеннолоппа - 02 мая 2020 в 19:28
|
|
Удаленный пользователь |
| 27 фев 2020 в 17:41 |
Сообщение удалено
лателеннолоппа
02 мая 2020 в 19:17
лателеннолоппа
02 мая 2020 в 19:17
Отредактировано: лателеннолоппа - 02 мая 2020 в 19:17
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 20:06 |
- ...
А вам известен алгоритм, по которому работает этот автоуровень? Какого результата вы от него хотите?
Картинки ваши не видно.
- -0.03 / 11
-
|
|
Удаленный пользователь |
| 27 фев 2020 в 21:07 |
Сообщение удалено
лателеннолоппа
02 мая 2020 в 19:27
лателеннолоппа
02 мая 2020 в 19:27
Отредактировано: лателеннолоппа - 02 мая 2020 в 19:27
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 21:30 |
- ...
То есть, вы уверены, что автоуровень способен скорректировать баланс белого?
- -0.12 / 13
-
|
|
Удаленный пользователь |
| 27 фев 2020 в 21:54 |
Сообщение удалено
лателеннолоппа
02 мая 2020 в 19:26
лателеннолоппа
02 мая 2020 в 19:26
Отредактировано: лателеннолоппа - 02 мая 2020 в 19:26
|
|
sharp89 ( Слушатель ) |
| 27 фев 2020 в 22:36 |
- ...
И как, по-вашему, эта программа может узнать, какой цвет брать за эталон серого?
- -0.05 / 14
-
|
|
Pаssаt ( Слушатель ) |
| 27 фев 2020 в 23:01 |
- ...
Интересно было бы узнать, на чем основана ваша уверенность? Вы хотя бы попробовали бы эту штуку на разных фотках, прежде, чем глупость сказать.
Я знаю, что нет. Алгоритм прост до безобразия. Гистограммы трех каналов изображения растягиваются до ширины от 0 до 255. Все.
Цвета плывут только так.
- -0.03 / 15
-
|
|
sharp89 ( Слушатель ) |
| 27 фев 2020 в 13:08 |
- ...
Цитата: viewer от 22.02.2020 08:30:36
Необработанные оригиналы сканов - в левой колонке.
Смотри внимательно. Где ты РАЗНЫЙ ЦВЕТ увидал?


- -0.08 / 17
-
|
|
viewer ( Слушатель ) |
| 27 фев 2020 в 13:47 |
- ...
Цитата: sharp89 от 27.02.2020 13:08:44
Почему на обращаемой плёнке, она же слайд, предназначенной для съёмки при солнечном освещении и проецировании в дальнейшем безо всяких фильтров получается изображение с настолько смещённым балансом белого, что его приходится дополнительно корректировать,
These scans are being done by NASA Johnson, with some post-processing by Kipp Teague. The film is scanned at 4096 x 4096 pixels per image. (See a discussion from Arizona State University about the scanning process.) Kipp reduced each digital image to approximately 2350 x 2350 pixels (equivalent to 300 dpi) and did minor adjustments of levels to ensure that (1) brightly lit areas of lunar soil were neutral grey, (2) objects with known colors (such as the CDR stripes or the LCRU blankets) looked right, and (3) information in bright or dark areas was not lost
Киппом (Тэйгом) были проделаны некие незначительные подстройки уровней, чтобы гарантированно были удовлетворены все три условия:
(1) Освещённые места на лунном грунте имели нейтрально серый цвет.

(2) Объекты с хорошо известным известным цветом - командирские нарукавные полосы

или плёнка теплозащитного покрытия

имели естественный цвет.
(3) Отсутствие потери детализации в светах и в тенях.
чтобы

- +0.18 / 16
-
|
|
sharp89 ( Слушатель ) |
| 27 фев 2020 в 13:53 |
- ...
Цитата: viewer от 27.02.2020 13:47:54
Куда эт ты запрыгал? С заездом про "разные" цвета соседних кадров всё? Ну так объявляй слив, можешь даже написать, что был наивно введён в заблуждение коллегой по цеху - неучным блогером
 А уже потом скачи на другие темы.
А уже потом скачи на другие темы.
- -0.03 / 19
-


